第二章 直角三角形的边角关系 专项训练 求锐角三角函数的常见类型(含答案)
文档属性
| 名称 | 第二章 直角三角形的边角关系 专项训练 求锐角三角函数的常见类型(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 15.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-27 17:36:21 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二章 直角三角形的边角关系
专项训练 求锐角三角函数的常见类型
一 直接用锐角三角函数的定义
1.如图,在 中,则 的正切值是( )
第1题图 第2题图
2.如图所示,在 中, 垂足是点 D,若
则 sinC 的值为______________.
3.如图所示,直线 与x轴交于点 A,与直线 交于点B.
(1)求点 B的坐标;
(2)求 的值.
二 利用同角或互余角三角函数之间的关系
4.已知∠A是锐角,且 则 tanA 的值是 ( )
5.在 Rt△ABC 中,∠C=则 cosB的值是 ( )
C.2
6.已知α为锐角,则 m的取值范围是 ( )
7.观察下列等式:
①
②
③
…;
根据上述规律,计算 _______________.
三 利用设参数的方法
8.如图,在 Rt△ABC中,∠C=90°,BC=3AC,则 sinB= ( )
B.3
9. 如图所示,在 Rt△ABC 中,∠B =90°,∠A=30°,以点 A为圆心,BC长为半径画弧,交 AB 于点 D,分别以点 A,D为圆心,AB长为半径画弧,两弧交于点 E,连接AE,DE,则 ∠EAD 的余弦值是 ( )
10.若想求 cos15°的值,可先画 Rt△ABC,使∠C=90°,∠BAC=30°,再延长CA 到D,使 DA=AB,连接 BD.请利用这些条件,求出 tan15°的值.
四 利用等角代换的方法
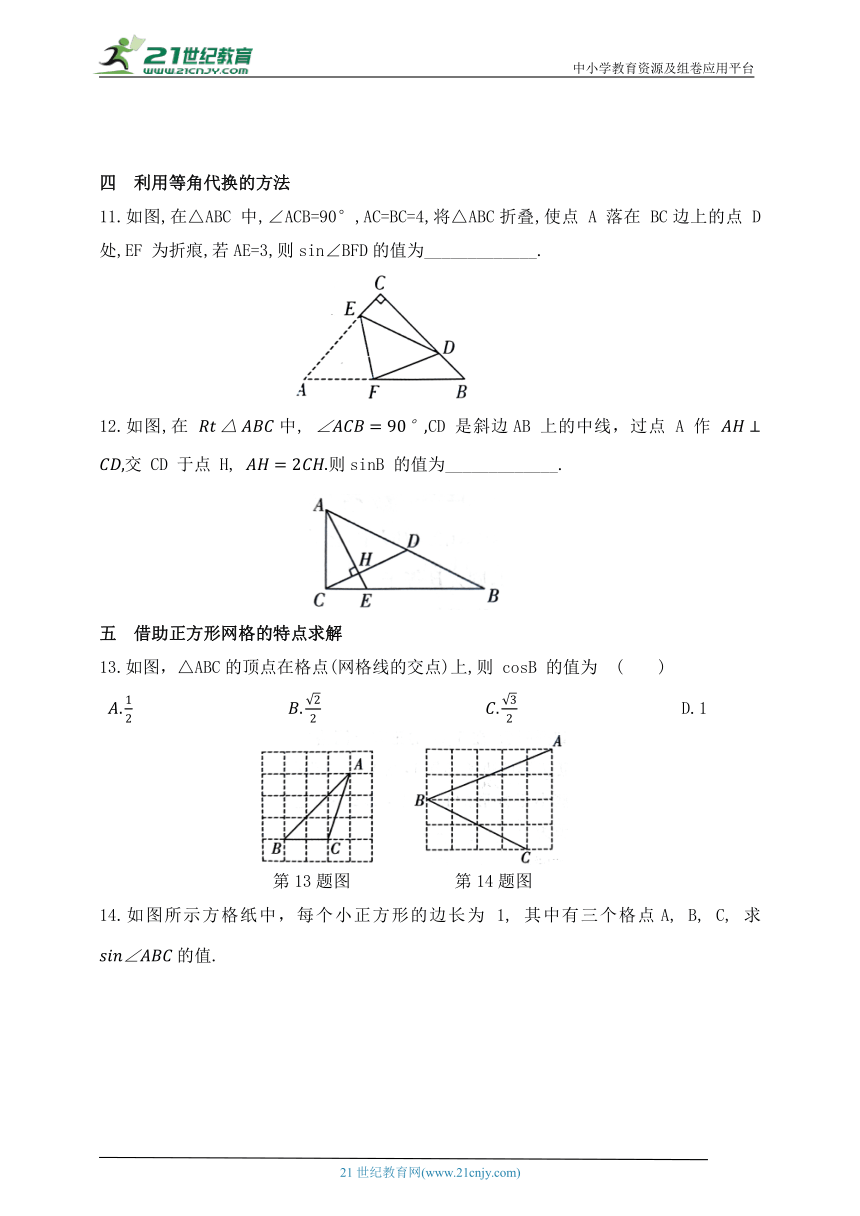
11.如图,在△ABC 中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点 A 落在 BC边上的点 D 处,EF 为折痕,若AE=3,则sin∠BFD的值为_____________.
12.如图,在 中, CD 是斜边AB 上的中线,过点 A 作 交 CD 于点 H, 则sinB 的值为_____________.
五 借助正方形网格的特点求解
13.如图,△ABC的顶点在格点(网格线的交点)上,则 cosB 的值为 ( )
D.1
第13题图 第14题图
14.如图所示方格纸中,每个小正方形的边长为 1, 其中有三个格点A, B, C, 求的值.
参考答案
1. C
3.解:(1)联立 解得
∴B点的坐标为(1,2);
(2)如图,过点 B 作 BC⊥x轴于点 C.
当y=0时, 解得x=-3,∴A(-3,0),∴OA=3.
∴AC=3+1=4,
4. D 5. A
6. A 解析:设在 中,
则
1
8. C
9.B 解析:如图,设
∵在 中,
由题意,得
作 EM⊥AD 于点 M,则
在 Rt△AEM中, (当点 E 在AB上方时同理)
10.解:∵AB=AD,∴∠D=∠ABD.
∵∠BAC=∠D+∠ABD,
设 BC=x.
在 Rt△ABC中,∵∠BAC=30°,∴AB=2x,
在 Rt△BDC 中,
13. B
14.解:如图,过点 A 作 AD⊥BC于点 D,连接AC.
A4=9,
解得 故
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二章 直角三角形的边角关系
专项训练 求锐角三角函数的常见类型
一 直接用锐角三角函数的定义
1.如图,在 中,则 的正切值是( )
第1题图 第2题图
2.如图所示,在 中, 垂足是点 D,若
则 sinC 的值为______________.
3.如图所示,直线 与x轴交于点 A,与直线 交于点B.
(1)求点 B的坐标;
(2)求 的值.
二 利用同角或互余角三角函数之间的关系
4.已知∠A是锐角,且 则 tanA 的值是 ( )
5.在 Rt△ABC 中,∠C=则 cosB的值是 ( )
C.2
6.已知α为锐角,则 m的取值范围是 ( )
7.观察下列等式:
①
②
③
…;
根据上述规律,计算 _______________.
三 利用设参数的方法
8.如图,在 Rt△ABC中,∠C=90°,BC=3AC,则 sinB= ( )
B.3
9. 如图所示,在 Rt△ABC 中,∠B =90°,∠A=30°,以点 A为圆心,BC长为半径画弧,交 AB 于点 D,分别以点 A,D为圆心,AB长为半径画弧,两弧交于点 E,连接AE,DE,则 ∠EAD 的余弦值是 ( )
10.若想求 cos15°的值,可先画 Rt△ABC,使∠C=90°,∠BAC=30°,再延长CA 到D,使 DA=AB,连接 BD.请利用这些条件,求出 tan15°的值.
四 利用等角代换的方法
11.如图,在△ABC 中,∠ACB=90°,AC=BC=4,将△ABC折叠,使点 A 落在 BC边上的点 D 处,EF 为折痕,若AE=3,则sin∠BFD的值为_____________.
12.如图,在 中, CD 是斜边AB 上的中线,过点 A 作 交 CD 于点 H, 则sinB 的值为_____________.
五 借助正方形网格的特点求解
13.如图,△ABC的顶点在格点(网格线的交点)上,则 cosB 的值为 ( )
D.1
第13题图 第14题图
14.如图所示方格纸中,每个小正方形的边长为 1, 其中有三个格点A, B, C, 求的值.
参考答案
1. C
3.解:(1)联立 解得
∴B点的坐标为(1,2);
(2)如图,过点 B 作 BC⊥x轴于点 C.
当y=0时, 解得x=-3,∴A(-3,0),∴OA=3.
∴AC=3+1=4,
4. D 5. A
6. A 解析:设在 中,
则
1
8. C
9.B 解析:如图,设
∵在 中,
由题意,得
作 EM⊥AD 于点 M,则
在 Rt△AEM中, (当点 E 在AB上方时同理)
10.解:∵AB=AD,∴∠D=∠ABD.
∵∠BAC=∠D+∠ABD,
设 BC=x.
在 Rt△ABC中,∵∠BAC=30°,∴AB=2x,
在 Rt△BDC 中,
13. B
14.解:如图,过点 A 作 AD⊥BC于点 D,连接AC.
A4=9,
解得 故
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
