轴对称习题课
图片预览

文档简介
课件12张PPT。垂直平分线习题课C'A'CAB'
ACBBMN例1、已知:如图,△ABC中,边AB、BC的垂直平分线交于点P
求证:PA=PB=PC P是否在边AC的垂直平分线上, 为什么?结论: 三角形三边垂直平分线交于一点,这一点到三角形三个顶点的距离相等。你能依据例1得到什么结论?证明:∵点P在线段AB的垂直平分线MN上,
∴PA=PB(?).
同理 PB=PC.
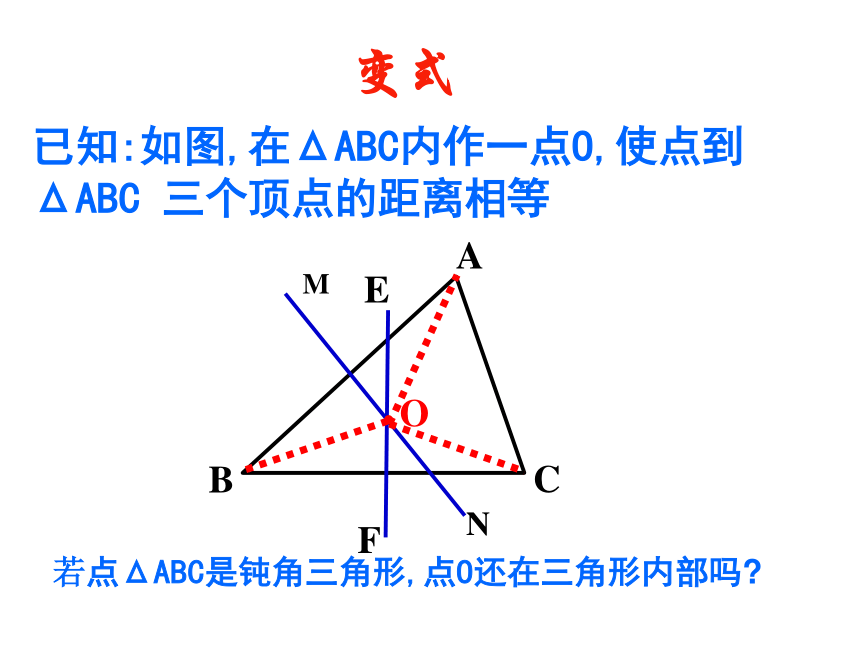
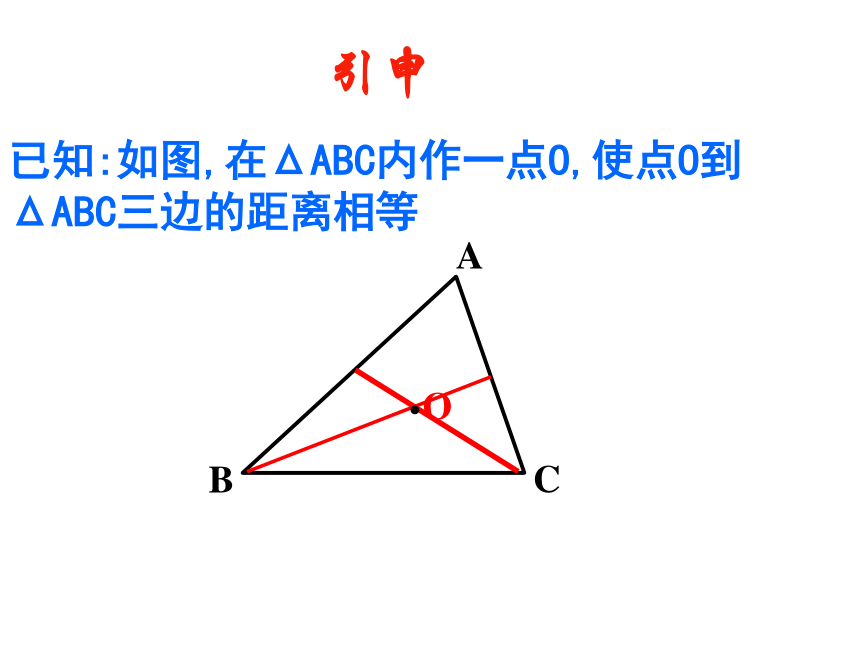
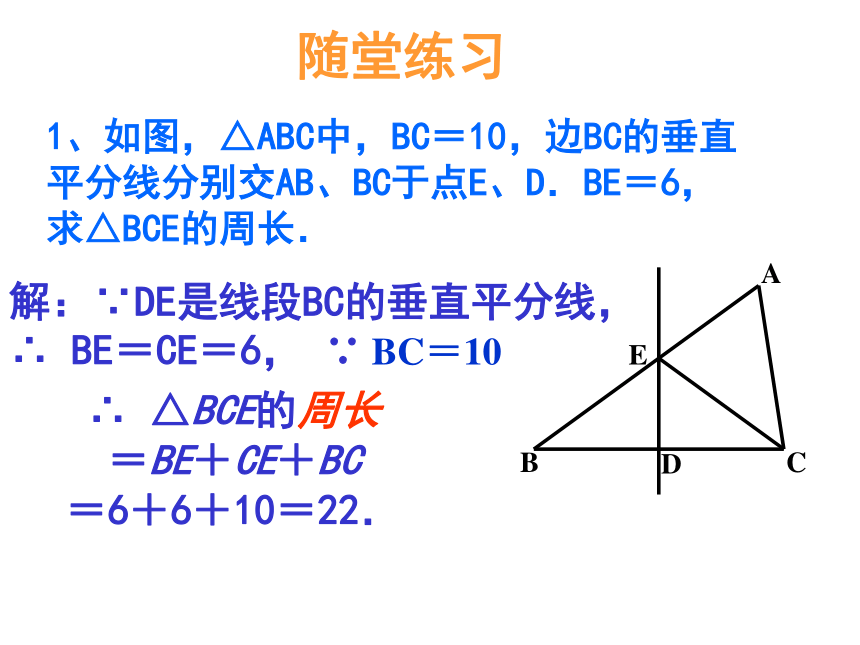
∴PA=PB=PC.已知:如图,在ΔABC内作一点O,使点到 ΔABC 三个顶点的距离相等BAC若点ΔABC是钝角三角形,点O还在三角形内部吗?变式已知:如图,在ΔABC内作一点O,使点O到 ΔABC三边的距离相等BAC引申1、如图,△ABC中,BC=10,边BC的垂直平分线分别交AB、BC于点E、D.BE=6,求△BCE的周长.解:∵DE是线段BC的垂直平分线,
∴ BE=CE=6, ∵ BC=10∴ △BCE的周长
=BE+CE+BC
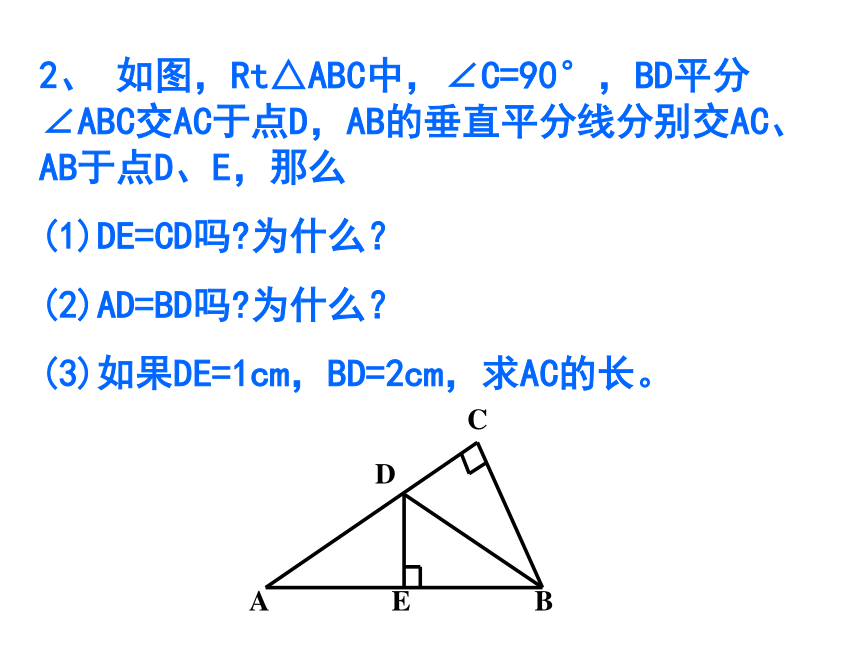
=6+6+10=22.随堂练习2、 如图,Rt△ABC中,∠C=90°,BD平分∠ABC交AC于点D,AB的垂直平分线分别交AC、AB于点D、E,那么
(1)DE=CD吗?为什么?
(2)AD=BD吗?为什么?
(3)如果DE=1cm,BD=2cm,求AC的长。3.如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,AB、AC、CE的长度有什么关系?AB+BD与DE有什么关系?4.如图所示,在△ABC中,AB=AC=32,MN是AB的垂直平分线,且有BC=21,求△BCN的周长。例2、已知:在ΔABC中,ON是AB的垂直平分线且OA=OC。求证:点O在BC的垂直平分线上。ABCON证明:连结OB。
∵ ON是AB的垂直平分线(已知)
∴ OA=OB(线段的垂直平分线上的点和这条线段的两个端点的距离相等)
∵ OA=OC(已知)
∴ OB=OC(等量代换)
∴点O在BC的垂直平分线上。
(和一条线段的两个端点距离相等的点,在这条线段的垂直平分线上。)1.如图,AB=AC,MB=MC,直线AM是线段 BC的垂直平分线吗?解:直线AM是线段 BC的垂直平分线。
∵ AB=AC
∴点A在线段 BC的垂直平分线上
∵ MB=MC
∴点M在线段 BC的垂直平分线上
∵两点确定一条直线,线段的中垂线有且只有一条
∴直线AM是线段 BC的垂直平分线挑战题C
B
2.如图:△ABC中, ∠ACB=90°,AD平分∠BAC,DE⊥AB于E,
求证:直线AD是CE的垂直平分线.挑战题3.如图, D ABC中,AD平分D BAC,DG ^ BC且平分BC交BC于G,DE ^ AB于E,
DF ^ AC于F.
证明:BE=CF
ACBBMN例1、已知:如图,△ABC中,边AB、BC的垂直平分线交于点P
求证:PA=PB=PC P是否在边AC的垂直平分线上, 为什么?结论: 三角形三边垂直平分线交于一点,这一点到三角形三个顶点的距离相等。你能依据例1得到什么结论?证明:∵点P在线段AB的垂直平分线MN上,
∴PA=PB(?).
同理 PB=PC.
∴PA=PB=PC.已知:如图,在ΔABC内作一点O,使点到 ΔABC 三个顶点的距离相等BAC若点ΔABC是钝角三角形,点O还在三角形内部吗?变式已知:如图,在ΔABC内作一点O,使点O到 ΔABC三边的距离相等BAC引申1、如图,△ABC中,BC=10,边BC的垂直平分线分别交AB、BC于点E、D.BE=6,求△BCE的周长.解:∵DE是线段BC的垂直平分线,
∴ BE=CE=6, ∵ BC=10∴ △BCE的周长
=BE+CE+BC
=6+6+10=22.随堂练习2、 如图,Rt△ABC中,∠C=90°,BD平分∠ABC交AC于点D,AB的垂直平分线分别交AC、AB于点D、E,那么
(1)DE=CD吗?为什么?
(2)AD=BD吗?为什么?
(3)如果DE=1cm,BD=2cm,求AC的长。3.如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,AB、AC、CE的长度有什么关系?AB+BD与DE有什么关系?4.如图所示,在△ABC中,AB=AC=32,MN是AB的垂直平分线,且有BC=21,求△BCN的周长。例2、已知:在ΔABC中,ON是AB的垂直平分线且OA=OC。求证:点O在BC的垂直平分线上。ABCON证明:连结OB。
∵ ON是AB的垂直平分线(已知)
∴ OA=OB(线段的垂直平分线上的点和这条线段的两个端点的距离相等)
∵ OA=OC(已知)
∴ OB=OC(等量代换)
∴点O在BC的垂直平分线上。
(和一条线段的两个端点距离相等的点,在这条线段的垂直平分线上。)1.如图,AB=AC,MB=MC,直线AM是线段 BC的垂直平分线吗?解:直线AM是线段 BC的垂直平分线。
∵ AB=AC
∴点A在线段 BC的垂直平分线上
∵ MB=MC
∴点M在线段 BC的垂直平分线上
∵两点确定一条直线,线段的中垂线有且只有一条
∴直线AM是线段 BC的垂直平分线挑战题C
B
2.如图:△ABC中, ∠ACB=90°,AD平分∠BAC,DE⊥AB于E,
求证:直线AD是CE的垂直平分线.挑战题3.如图, D ABC中,AD平分D BAC,DG ^ BC且平分BC交BC于G,DE ^ AB于E,
DF ^ AC于F.
证明:BE=CF
