2023-2024学年福建省厦门市高一(下)期末物理试卷(含答案)
文档属性
| 名称 | 2023-2024学年福建省厦门市高一(下)期末物理试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 305.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-07-27 22:25:45 | ||
图片预览



文档简介
2023-2024学年福建省厦门市高一(下)期末物理试卷
一、单选题:本大题共4小题,共16分。
1.引体向上是一种很好的力量训练运动,某同学完成一次引体向上标准动作用时,其中上升过程用时,重心上升的高度约为,则( )
A. 完成一次引体向上,重力对该同学一直做正功
B. 完成一次引体向上,重力对该同学一直做负功
C. 上升过程中该同学克服重力做功的平均功率约为
D. 上升过程中该同学克服重力做功的平均功率约为
2.如图所示,、两颗人造卫星绕地球做匀速圆周运动,已知卫星的轨道半径小于卫星的轨道半径,则( )
A. 卫星的周期小于卫星的周期
B. 卫星的线速度小于卫星的线速度
C. 卫星的向心加速度小于卫星的向心加速度
D. 卫星的线速度在之间
3.人工智能技术正加速与实体场景深度融合,一无人快递配送车在测试时,以恒定的加速度由静止匀加速启动,达到额定功率后保持恒定功率行驶至最大速度,该过程的图像用图线表示。若以加速度由静止匀加速启动,其他条件不变,其图像用图线表示,两次测试过程中配送车所受阻力相同且恒定,则下列图像中可能正确的是( )
A. B.
C. D.
4.如图所示,轻绳通过固定的轻质小滑轮,一端与套在光滑竖直杆上的物块连接,另一端与小球连接,初始时轻绳段长度为且与水平方向夹角为,将物块由静止释放,在下降过程中小球始终没有与相撞。已知物块与小球的质量均为,重力加速度取,忽略一切摩擦,则由静止释放到细绳段与水平方向夹角再次为的过程中,轻绳对物块所做的功为( )
A. B. C. D.
二、多选题:本大题共4小题,共24分。
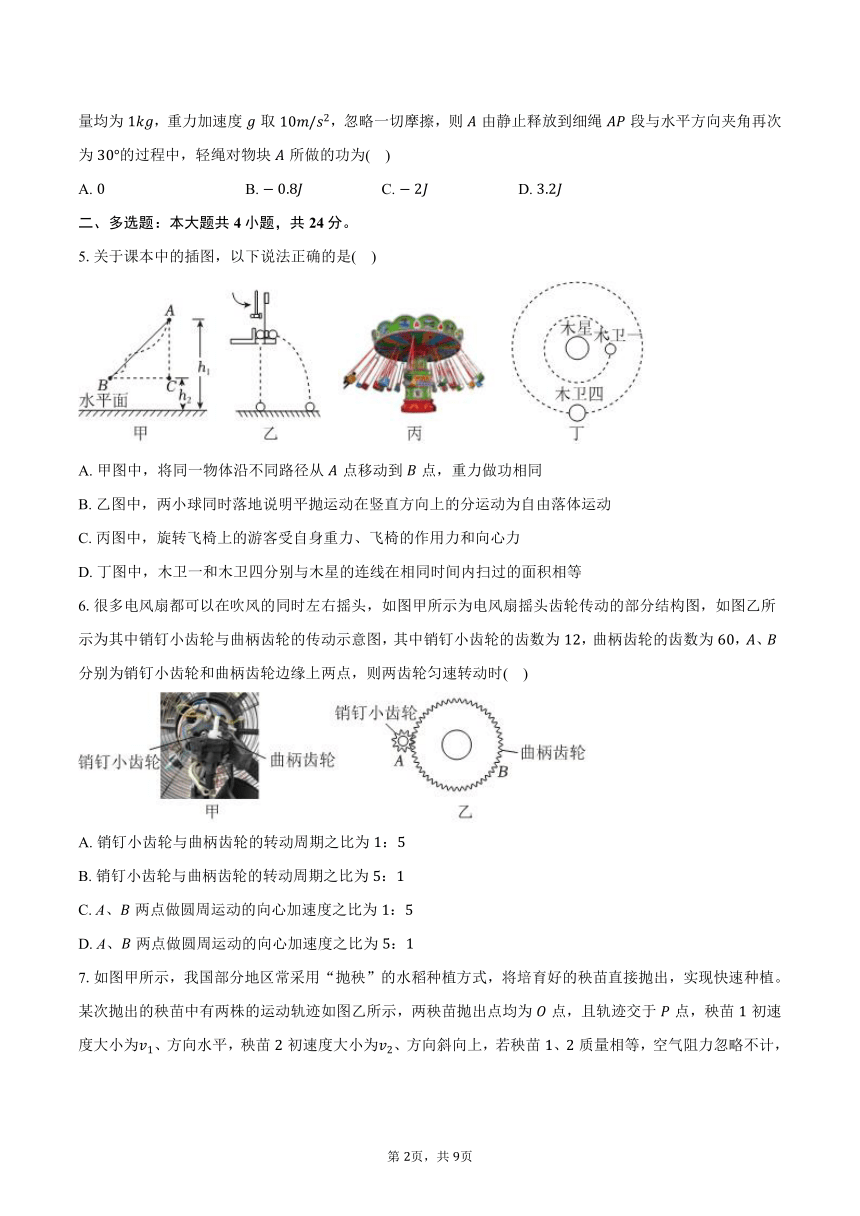
5.关于课本中的插图,以下说法正确的是( )
A. 甲图中,将同一物体沿不同路径从点移动到点,重力做功相同
B. 乙图中,两小球同时落地说明平抛运动在竖直方向上的分运动为自由落体运动
C. 丙图中,旋转飞椅上的游客受自身重力、飞椅的作用力和向心力
D. 丁图中,木卫一和木卫四分别与木星的连线在相同时间内扫过的面积相等
6.很多电风扇都可以在吹风的同时左右摇头,如图甲所示为电风扇摇头齿轮传动的部分结构图,如图乙所示为其中销钉小齿轮与曲柄齿轮的传动示意图,其中销钉小齿轮的齿数为,曲柄齿轮的齿数为,、分别为销钉小齿轮和曲柄齿轮边缘上两点,则两齿轮匀速转动时( )
A. 销钉小齿轮与曲柄齿轮的转动周期之比为:
B. 销钉小齿轮与曲柄齿轮的转动周期之比为:
C. A、两点做圆周运动的向心加速度之比为:
D. A、两点做圆周运动的向心加速度之比为:
7.如图甲所示,我国部分地区常采用“抛秧”的水稻种植方式,将培育好的秧苗直接抛出,实现快速种植。某次抛出的秧苗中有两株的运动轨迹如图乙所示,两秧苗抛出点均为点,且轨迹交于点,秧苗初速度大小为、方向水平,秧苗初速度大小为、方向斜向上,若秧苗、质量相等,空气阻力忽略不计,则( )
A. 两秧苗在空中运动时的加速度相同
B. 两秧苗从点运动到点所用时间相同
C. 在点处,秧苗的速度与水平方向夹角比秧苗的大
D. 在点处,秧苗重力的瞬时功率比秧苗的小
8.一轻质弹簧竖直悬挂,上端固定在天花板上,下端连接一质量为的小球。如图甲所示,将小球从某处由静止释放,以小球释放的位置为坐标原点,竖直向下为正方向建立轴,小球向下运动过程中加速度随位移变化的图像如图乙所示。已知重力加速度为,不计空气阻力,则( )
A. 小球下落过程中的机械能守恒 B. 弹簧的劲度系数
C. 小球运动过程中速度的最大值为 D. 小球向下运动的最大位移大于
三、填空题:本大题共3小题,共9分。
9.旋转木马是许多人童年时非常喜欢的游玩项目,如图所示,当转盘稳定运行时,木马绕转盘中心轴做圆周运动的同时也沿着竖直杆上下移动。已知旋转木马转盘稳定运行时,转了圈,则该转盘做圆周运动的周期为______;其中一匹木马做圆周运动的半径为,某时刻该木马沿杆向下运动的速度大小为,则此时该木马的实际速度大小为______取。
10.年,爱因斯坦基于广义相对论预言了引力波的存在,年,人类第一次直接探测到来自双中子里合并的引力波。两颗中子星合并前可视为双星系统,以两者连线上某点为圆心做匀速圆周运动。已知两颗中子星质量之比::,且均视为质量均匀分布的球体,则这两颗中子星做匀速圆周运动的角速度之比: ______,半径之比: ______。
11.如图所示,轻绳一端连接小球,穿过内壁光滑的竖直细管后另一端与质量为的小球连接,某同学握住细管,使小球在水平面内做匀速圆周运动,小球保持静止。稳定时轻绳段长为、与竖直方向夹角为,重力加速度取,则小球的质量为______,做圆周运动的角速度为______。
三、实验题:本大题共2小题,共13分。
12.小悟同学用如图甲所示装置研究平抛运动的特点,将白纸和复写纸重叠并固定在竖直硬板上,钢球沿斜槽轨道滑下后水平飞出,落在水平挡板上,在白纸上压出一个痕迹点。向下移动挡板,重新释放钢球,如此重复实验,白纸上将留下一系列痕迹点。
关于该实验,下列说法正确的有______。
A.斜槽轨道必须光滑
B.斜槽末端必须水平
C.每次从斜槽上相同位置无初速度释放钢球
D.描绘钢球平抛运动轨迹时应用折线将所有痕迹点连接起来
在某次实验中,小悟同学从斜槽同一位置由静止释放小球,将水平挡板依次固定在如图乙所示的竖直等间距的、、位置,在白纸上得到、、三个痕迹点,与、与的水平距离分别为和,则 ______选填“”“”或“”。
小悟同学通过上面实验装置,在白纸上画出了小球平抛运动的轨迹,轨迹的一部分如图丙所示,其中轴沿水平方向,轴沿竖直方向,当地重力加速度,由图中所给的数据可求出小球的初速度大小 ______。
13.小悟同学在实验室利用重锤自由下落来验证机械能守恒定律。
下列四幅图片为释放纸带前瞬间拍摄的照片,其中实验操作正确的是______。
选取合适的纸带,在纸带上选取连续的五个点、、、、,测得各点与起始点的距离,如图甲所示。已知重锤质量为,打点计时器的频率为,当地重力加速度,则从点到点重锤减少的重力势能为______,打下点时重锤的动能为______计算结果均保留位有效数字。
小悟同学重复两次实验,得到了两条纸带,测出各测量点到起始点的距离,计算出打下各测量点时重锤的速度,作出两次实验的图线分别如图乙中、所示,则这两次实验中误差较小的是______选填“”或“”。
四、计算题:本大题共3小题,共38分。
14.扔沙包是我国一种民间传统游戏,不仅能锻炼儿童投掷能力,还能训练手眼协调等能力。如图所示,某儿童将质量的沙包水平抛出,抛出点离水平地面的高度,沙包落地点与抛出点的水平距离,重力加速度取,不计沙包大小及空气阻力,求:
从抛出到落地的过程中重力对沙包所做的功;
沙包水平抛出的初速度大小;
沙包落地时速度的大小。
15.年月日,“嫦娥六号”月球探测器顺利进入大椭圆环月轨道Ⅰ运行,经过多次调整后,最终转入圆形环月轨道Ⅱ绕月球做匀速圆周运动。轨道Ⅰ、Ⅱ相切于近月点,轨道Ⅰ的远月点为,已知“嫦娥六号”在轨道Ⅰ、Ⅱ运行的周期分别为和,月球质量为,月球半径为,万有引力常量为,忽略月球自转,求:
月球表面的重力加速度大小;
圆形环月轨道Ⅱ的半径;
大椭圆环月轨道Ⅰ上的远月点到月球球心的距离。
16.如图甲所示为某同学制作的一套小型实验装置,该装置由弧形轨道、半径的竖直圆轨道、长度的水平直轨道、半径的圆弧轨道及倾斜传送带平滑连接而成。圆轨道出入口略微错开,圆弧轨道对应的圆心角,倾斜传送带的上表面在点与圆弧相切。质量的物块从弧形轨道离地高处由静止释放,物块与水平直轨道间的动摩擦因数,轨道、以及均光滑,物块视为质点,重力加速度取,,。
若,求物块经过竖直圆轨道点时所受轨道支持力的大小;
求出物块能沿轨道运动到点的最小释放高度;
将物块从处由静止释放,当传送带没有运行时,物块恰好能够到达传送带顶端,且物块在传送带上滑动过程中的机械能随位移变化的图像如图乙所示以水平直轨道所在的平面为零势能面。现让传送带以的速度顺时针运行,再次将物块从处静止释放,求物块此次在传送带上运动的过程中对传送带所做的功。
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.: :
11.
12.
13.
14.解:重力做功,代入数据得;
沙包做平抛运动,竖直方向上,水平方向上
代入数据解得
由动能定理得,代入数据解得
答:从抛出到落地的过程中重力对沙包所做的功为;
沙包水平抛出的初速度大小为;
沙包落地时速度的大小。
15.解:设月球表面有一质量为的物体,月球表面的重力加速度大小为,根据万有引力等于重力,有
解得月球表面的重力加速度大小为
设“嫦娥六号”的质量为,圆形环月轨道Ⅱ的半径为,在轨道Ⅱ上,“嫦娥六号”绕月球做匀速圆周运动,根据万有引力提供向心力,有
解得圆形环月轨道Ⅱ的半径为
设大椭圆环月轨道Ⅰ上的远月点到月球球心的距离为,根据开普勒第三定律有
解得
答:月球表面的重力加速度大小为;
圆形环月轨道Ⅱ的半径为;
大椭圆环月轨道Ⅰ上的远月点到月球球心的距离为。
16.解:物块从弧形轨道上高度为处由静止释放,到达点的过程,根据机械能守恒定律得:
解得物块到达点的速度大小为:
在点,物块受到重力和轨道的支持力,根据牛顿第二定律有:
解得:
设物块从弧形轨道上高度为时,能恰好通过竖直圆轨道的最高点,此情况在点所需向心力等于重力,则有:
物块从静止释放到点的过程,根据机械能守恒定律得:
解得:
假设物块从弧形轨道上高度为时,能沿轨道恰好运动到点,对整个过程,根据动能定理得:
解得:
因,故物块能沿轨道运动到点的最小释放高度。
由图乙可知物块在点的重力势能为,设点与轨道的高度差为,则有:,解得:
由几何关系得传送带的长度为:,解得:
设物块与传送带之间的动摩擦因数为,当传送带没有运行时,物块从处静止释放到传送带顶端的过程,根据动能定理得:
解得:
设物块到达点的速度大小为,同理可得:
解得:
当传送带以的速度顺时针运行时,设经过时间物块与传送带共速,共速前物块在传送带上运动的加速度大小为,根据牛顿第二定律与运动学公式得:
解得:
共速前传送带的位移大小为:
解得:
共速前物块在传送带上运动的过程对传送带所做的功为:
,解得:
共速前物块在传送带运动的位移大小为:
解得:
因,即,故共速后物块与传送带相对静止一起做匀速直线运动,共速后物块在传送带上运动的过程对传送带所做的功为:
,解得:
物块此次在传送带上运动的过程中对传送带所做的功为:
答:物块经过竖直圆轨道点时所受轨道支持力的大小;
出物块能沿轨道运动到点的最小释放高度为;
物块此次在传送带上运动的过程中对传送带所做的功为。
第1页,共1页
一、单选题:本大题共4小题,共16分。
1.引体向上是一种很好的力量训练运动,某同学完成一次引体向上标准动作用时,其中上升过程用时,重心上升的高度约为,则( )
A. 完成一次引体向上,重力对该同学一直做正功
B. 完成一次引体向上,重力对该同学一直做负功
C. 上升过程中该同学克服重力做功的平均功率约为
D. 上升过程中该同学克服重力做功的平均功率约为
2.如图所示,、两颗人造卫星绕地球做匀速圆周运动,已知卫星的轨道半径小于卫星的轨道半径,则( )
A. 卫星的周期小于卫星的周期
B. 卫星的线速度小于卫星的线速度
C. 卫星的向心加速度小于卫星的向心加速度
D. 卫星的线速度在之间
3.人工智能技术正加速与实体场景深度融合,一无人快递配送车在测试时,以恒定的加速度由静止匀加速启动,达到额定功率后保持恒定功率行驶至最大速度,该过程的图像用图线表示。若以加速度由静止匀加速启动,其他条件不变,其图像用图线表示,两次测试过程中配送车所受阻力相同且恒定,则下列图像中可能正确的是( )
A. B.
C. D.
4.如图所示,轻绳通过固定的轻质小滑轮,一端与套在光滑竖直杆上的物块连接,另一端与小球连接,初始时轻绳段长度为且与水平方向夹角为,将物块由静止释放,在下降过程中小球始终没有与相撞。已知物块与小球的质量均为,重力加速度取,忽略一切摩擦,则由静止释放到细绳段与水平方向夹角再次为的过程中,轻绳对物块所做的功为( )
A. B. C. D.
二、多选题:本大题共4小题,共24分。
5.关于课本中的插图,以下说法正确的是( )
A. 甲图中,将同一物体沿不同路径从点移动到点,重力做功相同
B. 乙图中,两小球同时落地说明平抛运动在竖直方向上的分运动为自由落体运动
C. 丙图中,旋转飞椅上的游客受自身重力、飞椅的作用力和向心力
D. 丁图中,木卫一和木卫四分别与木星的连线在相同时间内扫过的面积相等
6.很多电风扇都可以在吹风的同时左右摇头,如图甲所示为电风扇摇头齿轮传动的部分结构图,如图乙所示为其中销钉小齿轮与曲柄齿轮的传动示意图,其中销钉小齿轮的齿数为,曲柄齿轮的齿数为,、分别为销钉小齿轮和曲柄齿轮边缘上两点,则两齿轮匀速转动时( )
A. 销钉小齿轮与曲柄齿轮的转动周期之比为:
B. 销钉小齿轮与曲柄齿轮的转动周期之比为:
C. A、两点做圆周运动的向心加速度之比为:
D. A、两点做圆周运动的向心加速度之比为:
7.如图甲所示,我国部分地区常采用“抛秧”的水稻种植方式,将培育好的秧苗直接抛出,实现快速种植。某次抛出的秧苗中有两株的运动轨迹如图乙所示,两秧苗抛出点均为点,且轨迹交于点,秧苗初速度大小为、方向水平,秧苗初速度大小为、方向斜向上,若秧苗、质量相等,空气阻力忽略不计,则( )
A. 两秧苗在空中运动时的加速度相同
B. 两秧苗从点运动到点所用时间相同
C. 在点处,秧苗的速度与水平方向夹角比秧苗的大
D. 在点处,秧苗重力的瞬时功率比秧苗的小
8.一轻质弹簧竖直悬挂,上端固定在天花板上,下端连接一质量为的小球。如图甲所示,将小球从某处由静止释放,以小球释放的位置为坐标原点,竖直向下为正方向建立轴,小球向下运动过程中加速度随位移变化的图像如图乙所示。已知重力加速度为,不计空气阻力,则( )
A. 小球下落过程中的机械能守恒 B. 弹簧的劲度系数
C. 小球运动过程中速度的最大值为 D. 小球向下运动的最大位移大于
三、填空题:本大题共3小题,共9分。
9.旋转木马是许多人童年时非常喜欢的游玩项目,如图所示,当转盘稳定运行时,木马绕转盘中心轴做圆周运动的同时也沿着竖直杆上下移动。已知旋转木马转盘稳定运行时,转了圈,则该转盘做圆周运动的周期为______;其中一匹木马做圆周运动的半径为,某时刻该木马沿杆向下运动的速度大小为,则此时该木马的实际速度大小为______取。
10.年,爱因斯坦基于广义相对论预言了引力波的存在,年,人类第一次直接探测到来自双中子里合并的引力波。两颗中子星合并前可视为双星系统,以两者连线上某点为圆心做匀速圆周运动。已知两颗中子星质量之比::,且均视为质量均匀分布的球体,则这两颗中子星做匀速圆周运动的角速度之比: ______,半径之比: ______。
11.如图所示,轻绳一端连接小球,穿过内壁光滑的竖直细管后另一端与质量为的小球连接,某同学握住细管,使小球在水平面内做匀速圆周运动,小球保持静止。稳定时轻绳段长为、与竖直方向夹角为,重力加速度取,则小球的质量为______,做圆周运动的角速度为______。
三、实验题:本大题共2小题,共13分。
12.小悟同学用如图甲所示装置研究平抛运动的特点,将白纸和复写纸重叠并固定在竖直硬板上,钢球沿斜槽轨道滑下后水平飞出,落在水平挡板上,在白纸上压出一个痕迹点。向下移动挡板,重新释放钢球,如此重复实验,白纸上将留下一系列痕迹点。
关于该实验,下列说法正确的有______。
A.斜槽轨道必须光滑
B.斜槽末端必须水平
C.每次从斜槽上相同位置无初速度释放钢球
D.描绘钢球平抛运动轨迹时应用折线将所有痕迹点连接起来
在某次实验中,小悟同学从斜槽同一位置由静止释放小球,将水平挡板依次固定在如图乙所示的竖直等间距的、、位置,在白纸上得到、、三个痕迹点,与、与的水平距离分别为和,则 ______选填“”“”或“”。
小悟同学通过上面实验装置,在白纸上画出了小球平抛运动的轨迹,轨迹的一部分如图丙所示,其中轴沿水平方向,轴沿竖直方向,当地重力加速度,由图中所给的数据可求出小球的初速度大小 ______。
13.小悟同学在实验室利用重锤自由下落来验证机械能守恒定律。
下列四幅图片为释放纸带前瞬间拍摄的照片,其中实验操作正确的是______。
选取合适的纸带,在纸带上选取连续的五个点、、、、,测得各点与起始点的距离,如图甲所示。已知重锤质量为,打点计时器的频率为,当地重力加速度,则从点到点重锤减少的重力势能为______,打下点时重锤的动能为______计算结果均保留位有效数字。
小悟同学重复两次实验,得到了两条纸带,测出各测量点到起始点的距离,计算出打下各测量点时重锤的速度,作出两次实验的图线分别如图乙中、所示,则这两次实验中误差较小的是______选填“”或“”。
四、计算题:本大题共3小题,共38分。
14.扔沙包是我国一种民间传统游戏,不仅能锻炼儿童投掷能力,还能训练手眼协调等能力。如图所示,某儿童将质量的沙包水平抛出,抛出点离水平地面的高度,沙包落地点与抛出点的水平距离,重力加速度取,不计沙包大小及空气阻力,求:
从抛出到落地的过程中重力对沙包所做的功;
沙包水平抛出的初速度大小;
沙包落地时速度的大小。
15.年月日,“嫦娥六号”月球探测器顺利进入大椭圆环月轨道Ⅰ运行,经过多次调整后,最终转入圆形环月轨道Ⅱ绕月球做匀速圆周运动。轨道Ⅰ、Ⅱ相切于近月点,轨道Ⅰ的远月点为,已知“嫦娥六号”在轨道Ⅰ、Ⅱ运行的周期分别为和,月球质量为,月球半径为,万有引力常量为,忽略月球自转,求:
月球表面的重力加速度大小;
圆形环月轨道Ⅱ的半径;
大椭圆环月轨道Ⅰ上的远月点到月球球心的距离。
16.如图甲所示为某同学制作的一套小型实验装置,该装置由弧形轨道、半径的竖直圆轨道、长度的水平直轨道、半径的圆弧轨道及倾斜传送带平滑连接而成。圆轨道出入口略微错开,圆弧轨道对应的圆心角,倾斜传送带的上表面在点与圆弧相切。质量的物块从弧形轨道离地高处由静止释放,物块与水平直轨道间的动摩擦因数,轨道、以及均光滑,物块视为质点,重力加速度取,,。
若,求物块经过竖直圆轨道点时所受轨道支持力的大小;
求出物块能沿轨道运动到点的最小释放高度;
将物块从处由静止释放,当传送带没有运行时,物块恰好能够到达传送带顶端,且物块在传送带上滑动过程中的机械能随位移变化的图像如图乙所示以水平直轨道所在的平面为零势能面。现让传送带以的速度顺时针运行,再次将物块从处静止释放,求物块此次在传送带上运动的过程中对传送带所做的功。
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.: :
11.
12.
13.
14.解:重力做功,代入数据得;
沙包做平抛运动,竖直方向上,水平方向上
代入数据解得
由动能定理得,代入数据解得
答:从抛出到落地的过程中重力对沙包所做的功为;
沙包水平抛出的初速度大小为;
沙包落地时速度的大小。
15.解:设月球表面有一质量为的物体,月球表面的重力加速度大小为,根据万有引力等于重力,有
解得月球表面的重力加速度大小为
设“嫦娥六号”的质量为,圆形环月轨道Ⅱ的半径为,在轨道Ⅱ上,“嫦娥六号”绕月球做匀速圆周运动,根据万有引力提供向心力,有
解得圆形环月轨道Ⅱ的半径为
设大椭圆环月轨道Ⅰ上的远月点到月球球心的距离为,根据开普勒第三定律有
解得
答:月球表面的重力加速度大小为;
圆形环月轨道Ⅱ的半径为;
大椭圆环月轨道Ⅰ上的远月点到月球球心的距离为。
16.解:物块从弧形轨道上高度为处由静止释放,到达点的过程,根据机械能守恒定律得:
解得物块到达点的速度大小为:
在点,物块受到重力和轨道的支持力,根据牛顿第二定律有:
解得:
设物块从弧形轨道上高度为时,能恰好通过竖直圆轨道的最高点,此情况在点所需向心力等于重力,则有:
物块从静止释放到点的过程,根据机械能守恒定律得:
解得:
假设物块从弧形轨道上高度为时,能沿轨道恰好运动到点,对整个过程,根据动能定理得:
解得:
因,故物块能沿轨道运动到点的最小释放高度。
由图乙可知物块在点的重力势能为,设点与轨道的高度差为,则有:,解得:
由几何关系得传送带的长度为:,解得:
设物块与传送带之间的动摩擦因数为,当传送带没有运行时,物块从处静止释放到传送带顶端的过程,根据动能定理得:
解得:
设物块到达点的速度大小为,同理可得:
解得:
当传送带以的速度顺时针运行时,设经过时间物块与传送带共速,共速前物块在传送带上运动的加速度大小为,根据牛顿第二定律与运动学公式得:
解得:
共速前传送带的位移大小为:
解得:
共速前物块在传送带上运动的过程对传送带所做的功为:
,解得:
共速前物块在传送带运动的位移大小为:
解得:
因,即,故共速后物块与传送带相对静止一起做匀速直线运动,共速后物块在传送带上运动的过程对传送带所做的功为:
,解得:
物块此次在传送带上运动的过程中对传送带所做的功为:
答:物块经过竖直圆轨道点时所受轨道支持力的大小;
出物块能沿轨道运动到点的最小释放高度为;
物块此次在传送带上运动的过程中对传送带所做的功为。
第1页,共1页
同课章节目录
