开学摸底测试卷(含答案)2024-2025学年数学六年级上册苏教版
文档属性
| 名称 | 开学摸底测试卷(含答案)2024-2025学年数学六年级上册苏教版 |  | |
| 格式 | docx | ||
| 文件大小 | 598.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-28 14:27:31 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
开学摸底测试卷-2024-2025学年数学六年级上册苏教版
考试范围:五年级下册
一、选择题
1.甲有枚邮票,乙有15枚邮票,如果乙再收集8枚邮票,那么两人的邮票数正好相等。下面等式正确的是( )。
A. B. C. D.
2.用5米长的花布做了6条同样大小的童裤,每条童裤用这块花布的( )。
A. B. C. D.
3.一个圆的半径由5分米变成8分米,圆的面积增加( )平方分米.
A.3 B.6 C.39 D.39π
4.有两根同样长的绳子。第一根先用去,再用去米;第二根先用去米,再用去余下的。那么( )。
A.第一根剩下的长 B.第二根剩下的长
C.两根剩下的一样长 D.无法确定
5.哥德巴赫猜想被誉为“数学皇冠上的明珠”,猜想认为:任何大于2的偶数都可以写成两个质数之和。下面的式子中反映这个猜想的是( )。
A.4=1+3 B.13=2+11 C.54=3+51 D.36=7+29
6.把一个圆剪拼成一个近似的长方形后,这个长方形的长是25.12厘米,原来圆的半径是( )厘米。
A.4 B.8 C.12.56 D.16
二、填空题
7.如果a-b=1(a、b均为非零自然数),那么a与b的最大公因数是( ),最小公倍数是( )。
8.25既是2的倍数,又是3的倍数,里最大可填( );15既是3的倍数,又是5的倍数,里可以填( )。
9.的分子除以2,要使分数的大小不变,分母应除以( );的分母加上40,要使分数的大小不变,分子应加上( )。
10.圆规两脚之间的距离是4cm,画出圆的周长是( )cm,面积是( )cm2。
11.的和是( );的积是( )。(填“奇数”或“偶数”)
12.如图1所示:一个黑色小球(用点P表示)以每秒2厘米的速度,从直角梯形的顶点A出发,沿着梯形ABCD的边匀速移动,先后途经B点、C点和D点,最终又回到A点。在点P移动的过程中,以P、A、B三点为丁点的三角形的面积也在不断变化。图2的统计图记录了点P移动时间和三角形PAB面积的变化情况。根据图中信息回答下列问题:
(1)图2中的a是( )平方厘米,c是( )平方厘米。
(2)图1中梯形ABCD的面积是( )平方厘米。
三、判断题
13.在同一个圆中,圆心角越小,扇形也越小.( )
14.因为>,所以的分数单位大于的分数单位. ( )
15.等式两边乘同一个数(0除外),左右两边仍然相等. ( )
16.0.9n÷4=18的解是n=12。( )
17.如果一个分数的分子和分母的最大公因数是1,那么这个分数就是最简分数。( )
四、计算题
18.直接写得数。
302= -= -= 2-=
0.22= 0.2+= += 1--=
19.能简算的要简算。
-+ 5-- 1-----
20.解方程。
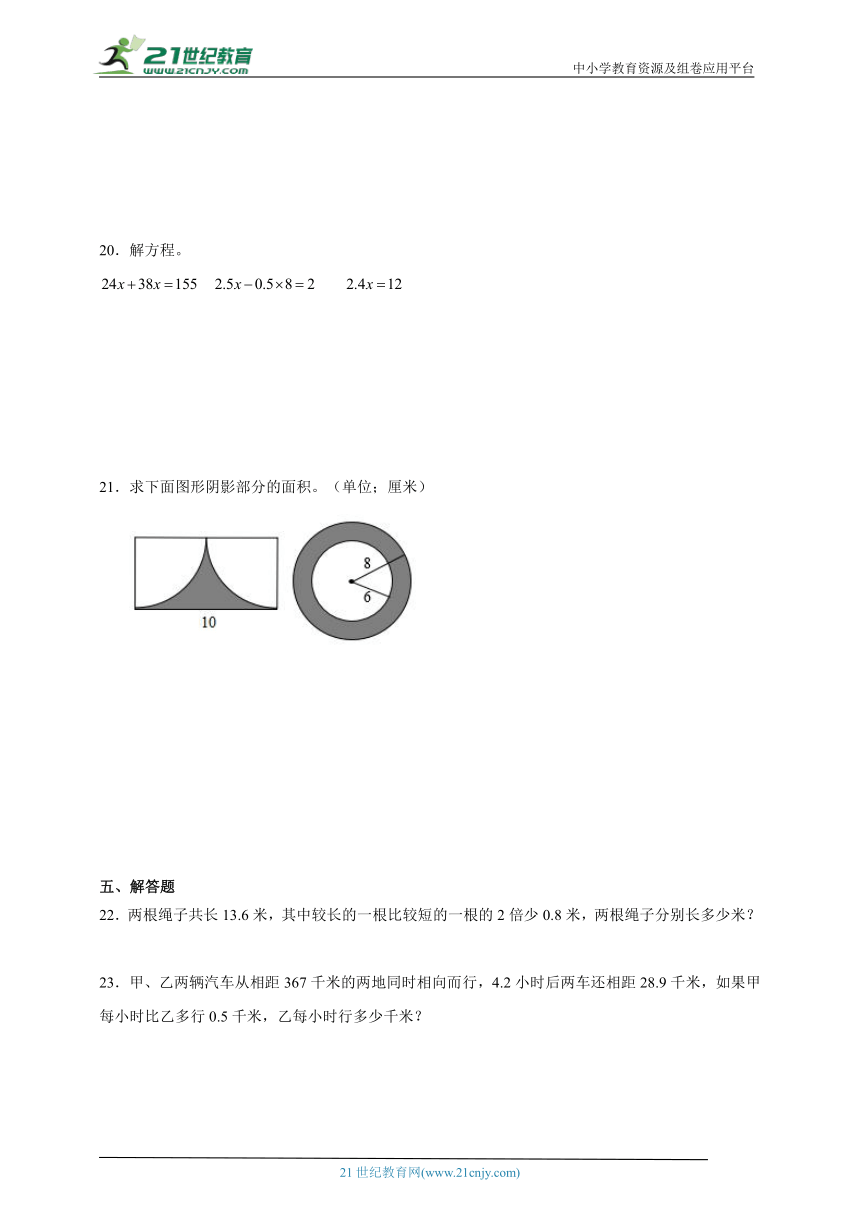
21.求下面图形阴影部分的面积。(单位;厘米)
五、解答题
22.两根绳子共长13.6米,其中较长的一根比较短的一根的2倍少0.8米,两根绳子分别长多少米?
23.甲、乙两辆汽车从相距367千米的两地同时相向而行,4.2小时后两车还相距28.9千米,如果甲每小时比乙多行0.5千米,乙每小时行多少千米?
24.妈妈买回一筐苹果,如果每天吃4个,则多出48个苹果;如果每天吃6个,则又少8个苹果。计划吃多少天?妈妈买回苹果多少个?
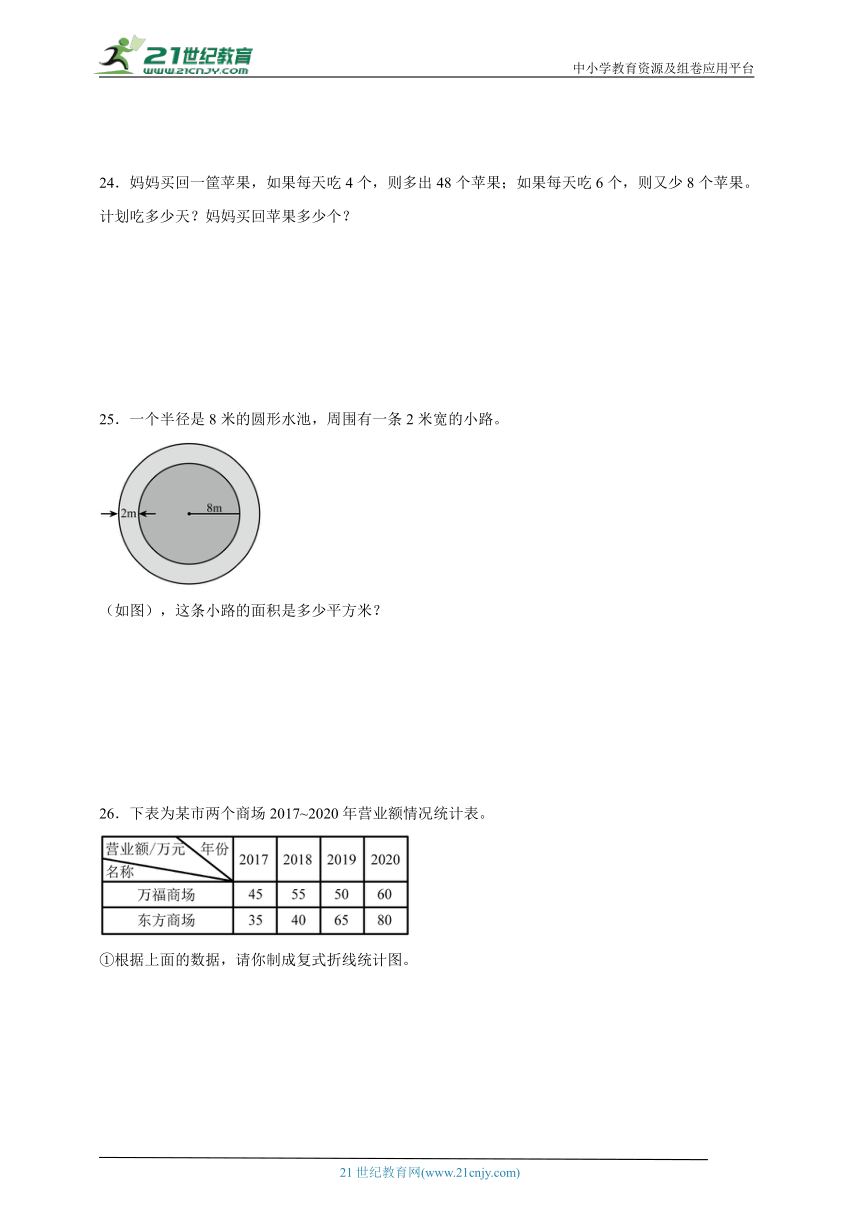
25.一个半径是8米的圆形水池,周围有一条2米宽的小路。
(如图),这条小路的面积是多少平方米?
26.下表为某市两个商场2017~2020年营业额情况统计表。
①根据上面的数据,请你制成复式折线统计图。
②万福商场在( )年营业额最多,在( )年营业额最少。
③东方商场在( )年营业额最多,( )年营业额增长最快。
参考答案:
1.A
【分析】乙再收集8枚,两人就一样多,则甲的邮票数量-乙再收集的邮票数量=乙原有的邮票数量,据此解答即可。
【详解】甲有枚邮票,乙有15枚邮票,如果乙再收集8枚邮票,那么两人的邮票数正好相等,则可列等式。
故答案为:A
【点睛】解决本题的关键是根据题意找出正确的等量关系式。
2.B
【分析】根据题意:把5米长的花布当作单位“1”,把单位“1”平均分成6份,每份是它的。据此解答。
【详解】由分析可知:每条童裤用这块花布的。
故答案为:B
【点睛】理解分数的意义是解答的关键。
3.D
【详解】用大圆的面积减去小圆的面积,即可求出圆的面积增加多少平方分米,根据此选择即可.
4.B
【分析】设这两根绳子的长度都是米,分别计算出每个绳子剩余的长度,结果用含有的式子表示,再比较大小。
【详解】第一根绳子还剩:
米
第二根绳子还剩:
米
,,因此
所以,第二根剩下的长。
故答案为:B
【点睛】本题解题关键是理解用去米与用去的意义是不同的,然后分别计算出每个绳子剩余的长度,结果用含有的式子表示,再比较大小。
5.D
【分析】根据质数的定义,除了1和本身外,没有其它因数的数叫质数;根据题意“这个猜想的内容是任何大于2的偶数都是两个质数之和”进行判断逐项分析即可。
【详解】A.“4=1+3”中1既不是质数,也不是合数,不符合猜想;
B.“13=2+11”中13是奇数,不是偶数,不符合猜想;
C.“54=3+51”中51是合数,不是质数,不符合猜想;
D.“36=17+19”中36是偶数,7和29是质数,符合猜想。
哥德巴赫猜想被誉为“数学皇冠上的明珠”,猜想认为:任何大于2的偶数都可以写成两个质数之和。下面的式子中反映这个猜想的是36=7+29。
故答案为:D
【点睛】此题考查了质数的意义以及拓展应用,要熟练掌握熟练掌握质数的意义是解答本题的关键。
6.B
【分析】根据圆的剪拼方法可得,长方形的长乘2就是圆的周长,根据圆的周长公式可以得出半径。
【详解】25.12×2÷3.14÷2
=50.12÷3.14÷2
=8(厘米)
原来圆的半径是8厘米。
故答案为:B
【点睛】由题意发现长方形的长乘就是圆的周长是解题的关键。
7. 1 ab
【分析】a-b=1,(a、b均为非零自然数),由此可知,a和b是相邻的两个数,即a和b是互质数,如果两个数为互质数,最大公因数是1,最小公倍数是两个数的乘积,据次解答。
【详解】根据分析可知,a与b是互质数,a和b的最大公因数是1,最小公倍数是ab。
如果a-b=1(a、b均为非零自然数),那么a与b的最大公因数是1,最小公倍数是ab。
【点睛】熟练掌握求两个数的最小公倍数和最大公因数的方法是解答本题的关键。
8. 8 0
【分析】既是2的倍数又是3的倍数的数的特征:个位上是0、2、4、6或8,且各个数位上的数字之和是3的倍数;既是3的倍数又是5的倍数的数的特征:个位上是0或5,且各个数位上的数字之和是3的倍数;依据此特征分析并填空即可。
【详解】25既是2的倍数又是3的倍数,则个位上是0、2、4、6或8,求里最大填几,从8开始试,2+5+8=15,15是3的倍数,那么258既是2的倍数又是3的倍数,即里最大填8;45既是3的倍数又是5的倍数,则个位上是0或5,4+5+0=9,9是3的倍数,4+5+5=14,14不是3的倍数,那么450既是3的倍数又是5的倍数,即里可以填0。
【点睛】此题重点考查2、5、3倍数的特征及灵活运用。
9. 2 25
【分析】根据分数的基本性质:分数的分子分母同时乘或除以一个不为0的数,分数的大小不边;的分子除以2,则分母也除以2;的分母加上40,得到的和再除以分母,求出分母扩大到原来的多少倍,分子也扩大到原来的多少倍,再用扩大后的分子减去原来的分子,即可解答。
【详解】的分子除以2,要使分数的大小不变,分母应除以2;
(8+40)÷8
=48÷8
=6
5×6-5
=30-5
=25
的分子除以2,要使分数的大小不变,分母应除以2;的分母加上40,要使分数的大小不变,分子应加上25。
【点睛】熟练掌握分数的基本性质是解答本题的关键。
10. 25.12 50.24
【分析】画圆时,圆规两脚间的距离即为半径长度,根据圆的周长公式:C=2r,圆的面积公式:S=r2,将数值代入计算即可。
【详解】由分析可得:
2×3.14×4
=6.28×4
=25.12(cm)
3.14×42
=3.14×16
=50.24(cm2)
综上所述:圆规两脚之间的距离是4cm,画出圆的周长是25.12cm,面积是50.24cm2。
【点睛】本题考查了用圆规画圆,圆规两脚之间的距离就是要画的圆的半径,同时需要牢记圆的周长和面积公式。
11. 奇数 偶数
【分析】奇数+奇数=偶数;奇数+偶数=奇数;偶数+偶数=偶数;奇数个奇数相加,和是奇数;偶数个奇数相加,和是偶数;第一空据此解答;
奇数×奇数=奇数;奇数×偶数=偶数;偶数×偶数=偶数;第二小空据此解答。
【详解】3+5+7+…+17+19是9个奇数相加,和是奇数;
2×19×23×37×111×239,2是偶数,19、23、37、111、239是奇数,2×19×23×37×111×239积是偶数。
的和是奇数;的积是偶数。
【点睛】熟练掌握运算性质(奇数和偶数)是解答本题的关键,
12.(1) 32 24
(2)72
【分析】(1)根据图可知,a对应的是8秒的时候,由于当P在AB段上移动时,P、A、B不能构成三角形,所以没有面积,即在第4秒的时候,开始有面积,说明第4秒走到了B点,那么AB的长度是:4×2=8(厘米),当P点走到C点的时候,三角形的面积是最大的,则此时走了10秒,当第8秒时,即在BC段走了4秒,那么此时的PB长是:4×2=8(厘米),高是AB的长度,根据三角形的面积公式:底×高÷2,即8×8÷2,即可求出a的值;当在10秒开始,三角形的面积下降,此时在CD线上,由于在15秒时,下降趋势变化,说明15秒时走到了D点,从D点到A点总共走了3秒,即AD的长度是3×2=6(厘米),高是AB的长度,即此时的c表示的数是:6×8÷2,据此即可求解;
(2)由于AD是6厘米,AB是8厘米,BC总共走了10-4=6(秒),即BC的长度是:6×2=12(厘米),根据梯形的面积公式:(上底+下底)×高÷2,把数代入即可求解。
【详解】(1)4×2=8(厘米)
(8-4)×2
=4×2
=8(厘米)
8×8÷2=32(平方厘米)
18-15=3(秒)
3×2=6(厘米)
6×8÷2=24(平方厘米)
图2中的a是32平方厘米,c是24平方厘米。
(2)10-4=6(秒)
6×2=12(厘米)
(6+12)×8÷2
=18×8÷2
=72(平方厘米)
图1中梯形ABCD的面积是72平方厘米。
【点睛】本题主要考查折线统计图的分析以及三角形和梯形的面积公式,关键是找准三角形的底和高的变化是解题的关键。
13.正确
【详解】同一个圆中,圆心角越小,扇形也越小.原题说法正确.故答案为正确.
14.
【详解】略
15.√
【详解】略
16.×
【分析】等式两边同时乘或除以同一个不是0的数,所得结果仍然是等式,这是等式的性质。由此计算出n的值即可。
【详解】0.9n÷4=18
0.9n÷4×4=18×4
0.9n=72
0.9n÷0.9=72÷0.9
n=80
0.9n÷4=18的解是n=80。原题说法错误。
故答案为:×
17.√
【分析】根据最简分数的含义进行分析,分子和分母只有公因数1,像这样的分数叫作最简分数。
【详解】如果一个分数的分子和分母的最大公因数是1,即分子和分母只有公因数1,那么这个分数就是最简分数。例如:,7和8的最大公因数是1,它是最简分数。说法正确。
故答案为:√
18.900;;;;
0.04;;;0
【详解】略
19.;3;
【分析】先通分再从左到右依次计算即可;
根据减法的性质进行简算;
原式化为:1-(1-)-(-)-(-)-(-)-(-),再根据减法的性质进行简算即可。
【详解】-+
=-+
=
5--
=5-(+)
=5-2
=3
1-----
=1-(1-)-(-)-(-)-(-)-(-)
=1-1+-+-+-+-+
=
20.x=2.5;x=2.4;x=5
【分析】合并方程左边同类项,再根据等式的性质2,方程的两边同时除以(24+38)即可;
根据等式的性质1,方程的两边同时加上0.5×8,再根据等式的性质2,方程的两边同时除以2.5即可;
根据等式的性质2,方程的两边同时除以2.4即可。
【详解】
解:(24+38)x=155
x=155÷62
x=2.5
解:2.5x=2+4
x=6÷2.5
x=2.4
解:x=12÷2.4
x=5
21.(1)10.75平方厘米(2)87.92平方厘米
【分析】(1)空白部分可以组成一个半圆,用长方形的面积减去半圆的面积即是阴影部分的面积。长方形的面积=长×宽,圆的面积=πr2,据此解答。要注意长方形的宽等于半圆的半径,是10÷2=5(厘米)。
(2)圆环的面积=π(R2-r2),据此解答。
【详解】(1)10÷2=5(厘米)
10×5-3.14×52÷2
=50-39.25
=10.75(平方厘米)
(2)3.14×(82-62)
=3.14×28
=87.92(平方厘米)
22.8.8米;4.8米
【分析】设较短的一根绳长x米,则较长的一根绳长(2x-0.8),两根绳长加起来共13.6米,根据这个等量关系列方程解答。
【详解】解:设较短的一根绳长x米。
x+(2x-0.8)=13.6
3x-0.8+0.8=13.6+0.8
3x÷3=14.4÷3
x=4.8
当x=4.8时,
2x-0.8
=2×4.8-0.8
=8.8(米)
答:较长的一根长8.8米,较短的一根长4.8米。
【点睛】解答本题还可以先用13.6米加上0.8米,再除以3,求出较短的绳长,进而求出较长的绳长。
23.40千米
【分析】设乙每小时行x千米,则甲每小时行(x+0.5)千米。根据题意,(甲的速度+乙的速度)×行驶时间+两车相距的路程=总路程,据此列方程即可解答。
【详解】解:设乙每小时行x千米。
(x+0.5+x)×4.2+28.9=367
(2x+0.5)×4.2+28.9=367
(2x+0.5)×4.2=367-28.9
(2x+0.5)×4.2=338.1
2x+0.5=338.1÷4.2
2x+0.5=80.5
2x=80.5-0.5
2x=80
x=80÷2
x=40
答:乙每小时行40千米。
【点睛】本题考查相遇问题。列方程解含有两个未知数的问题时,设其中的一个未知数是x,用含有x的式子表示另一个未知数,再根据等量关系即可列出方程。找出本题的等量关系式是解题的关键。
24.8天;160个
【分析】设计划吃x天,由“每天吃4个,则多长48个苹果”,可知苹果个数为4x+48个;由“每天吃6个,则又少8个苹果”可知,苹果个数为6x-8个;因为苹果个数相等,列方程:4x+48=6x-8,解方程,求出计划吃的天数,进而求出妈妈买回苹果的个数。
【详解】解:设计划吃x天。
4x+48=6x-8
6x-4x=48+8
2x=56
x=56÷2
x=28
4×28+48
=112+48
=160(个)
答:计划吃28天,妈妈买回苹果160个。
【点睛】本题考查方程的实际应用,根据苹果吃的天数和苹果的个数,设出未知数,找出相关的量,列方程,解方程。
25.113.04平方米
【分析】根据题意可知小路的内圆半径是8米,则外面半径是(8+2)米,根据圆环的面积公式:S=π(R2-r2),求出小路的面积即可。
【详解】8+2=10(米)
3.14×(102-82)
=3.14×(100-64)
=3.14×36
=113.04(平方米)
答:这条小路的面积是113.04平方米。
【点睛】本题考查的是圆环的面积公式的应用,明确大圆和小圆的半径是解题的关键。
26.①见详解
②2020;2017
③2020;2018~2019
【分析】①结合表格的数据,在统计图中描出每个商场营业额数据的点,然后再连线即可;
②将万福商场的各年份的营业额排序,找出最多与最少的数值即可;
③将东方商场的各年份的营业额排序,找出最多的数值;每两年之间的差额越大,营业额增长也就越快;
【详解】①
②60>55>50>45,所以万福商场在(2020)年营业额最多,在(2017)年营业额最少。
③80>65>40>35,
40-35=5(万元),65-40=25(万元),80-65=15(万元)
所以,东方商场在(2020)年营业额最多,(2018~2019)年营业额增长最快。
【点睛】此题考查了复式折线统计图的内容,关键能够根据图标获取正确的信息。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
开学摸底测试卷-2024-2025学年数学六年级上册苏教版
考试范围:五年级下册
一、选择题
1.甲有枚邮票,乙有15枚邮票,如果乙再收集8枚邮票,那么两人的邮票数正好相等。下面等式正确的是( )。
A. B. C. D.
2.用5米长的花布做了6条同样大小的童裤,每条童裤用这块花布的( )。
A. B. C. D.
3.一个圆的半径由5分米变成8分米,圆的面积增加( )平方分米.
A.3 B.6 C.39 D.39π
4.有两根同样长的绳子。第一根先用去,再用去米;第二根先用去米,再用去余下的。那么( )。
A.第一根剩下的长 B.第二根剩下的长
C.两根剩下的一样长 D.无法确定
5.哥德巴赫猜想被誉为“数学皇冠上的明珠”,猜想认为:任何大于2的偶数都可以写成两个质数之和。下面的式子中反映这个猜想的是( )。
A.4=1+3 B.13=2+11 C.54=3+51 D.36=7+29
6.把一个圆剪拼成一个近似的长方形后,这个长方形的长是25.12厘米,原来圆的半径是( )厘米。
A.4 B.8 C.12.56 D.16
二、填空题
7.如果a-b=1(a、b均为非零自然数),那么a与b的最大公因数是( ),最小公倍数是( )。
8.25既是2的倍数,又是3的倍数,里最大可填( );15既是3的倍数,又是5的倍数,里可以填( )。
9.的分子除以2,要使分数的大小不变,分母应除以( );的分母加上40,要使分数的大小不变,分子应加上( )。
10.圆规两脚之间的距离是4cm,画出圆的周长是( )cm,面积是( )cm2。
11.的和是( );的积是( )。(填“奇数”或“偶数”)
12.如图1所示:一个黑色小球(用点P表示)以每秒2厘米的速度,从直角梯形的顶点A出发,沿着梯形ABCD的边匀速移动,先后途经B点、C点和D点,最终又回到A点。在点P移动的过程中,以P、A、B三点为丁点的三角形的面积也在不断变化。图2的统计图记录了点P移动时间和三角形PAB面积的变化情况。根据图中信息回答下列问题:
(1)图2中的a是( )平方厘米,c是( )平方厘米。
(2)图1中梯形ABCD的面积是( )平方厘米。
三、判断题
13.在同一个圆中,圆心角越小,扇形也越小.( )
14.因为>,所以的分数单位大于的分数单位. ( )
15.等式两边乘同一个数(0除外),左右两边仍然相等. ( )
16.0.9n÷4=18的解是n=12。( )
17.如果一个分数的分子和分母的最大公因数是1,那么这个分数就是最简分数。( )
四、计算题
18.直接写得数。
302= -= -= 2-=
0.22= 0.2+= += 1--=
19.能简算的要简算。
-+ 5-- 1-----
20.解方程。
21.求下面图形阴影部分的面积。(单位;厘米)
五、解答题
22.两根绳子共长13.6米,其中较长的一根比较短的一根的2倍少0.8米,两根绳子分别长多少米?
23.甲、乙两辆汽车从相距367千米的两地同时相向而行,4.2小时后两车还相距28.9千米,如果甲每小时比乙多行0.5千米,乙每小时行多少千米?
24.妈妈买回一筐苹果,如果每天吃4个,则多出48个苹果;如果每天吃6个,则又少8个苹果。计划吃多少天?妈妈买回苹果多少个?
25.一个半径是8米的圆形水池,周围有一条2米宽的小路。
(如图),这条小路的面积是多少平方米?
26.下表为某市两个商场2017~2020年营业额情况统计表。
①根据上面的数据,请你制成复式折线统计图。
②万福商场在( )年营业额最多,在( )年营业额最少。
③东方商场在( )年营业额最多,( )年营业额增长最快。
参考答案:
1.A
【分析】乙再收集8枚,两人就一样多,则甲的邮票数量-乙再收集的邮票数量=乙原有的邮票数量,据此解答即可。
【详解】甲有枚邮票,乙有15枚邮票,如果乙再收集8枚邮票,那么两人的邮票数正好相等,则可列等式。
故答案为:A
【点睛】解决本题的关键是根据题意找出正确的等量关系式。
2.B
【分析】根据题意:把5米长的花布当作单位“1”,把单位“1”平均分成6份,每份是它的。据此解答。
【详解】由分析可知:每条童裤用这块花布的。
故答案为:B
【点睛】理解分数的意义是解答的关键。
3.D
【详解】用大圆的面积减去小圆的面积,即可求出圆的面积增加多少平方分米,根据此选择即可.
4.B
【分析】设这两根绳子的长度都是米,分别计算出每个绳子剩余的长度,结果用含有的式子表示,再比较大小。
【详解】第一根绳子还剩:
米
第二根绳子还剩:
米
,,因此
所以,第二根剩下的长。
故答案为:B
【点睛】本题解题关键是理解用去米与用去的意义是不同的,然后分别计算出每个绳子剩余的长度,结果用含有的式子表示,再比较大小。
5.D
【分析】根据质数的定义,除了1和本身外,没有其它因数的数叫质数;根据题意“这个猜想的内容是任何大于2的偶数都是两个质数之和”进行判断逐项分析即可。
【详解】A.“4=1+3”中1既不是质数,也不是合数,不符合猜想;
B.“13=2+11”中13是奇数,不是偶数,不符合猜想;
C.“54=3+51”中51是合数,不是质数,不符合猜想;
D.“36=17+19”中36是偶数,7和29是质数,符合猜想。
哥德巴赫猜想被誉为“数学皇冠上的明珠”,猜想认为:任何大于2的偶数都可以写成两个质数之和。下面的式子中反映这个猜想的是36=7+29。
故答案为:D
【点睛】此题考查了质数的意义以及拓展应用,要熟练掌握熟练掌握质数的意义是解答本题的关键。
6.B
【分析】根据圆的剪拼方法可得,长方形的长乘2就是圆的周长,根据圆的周长公式可以得出半径。
【详解】25.12×2÷3.14÷2
=50.12÷3.14÷2
=8(厘米)
原来圆的半径是8厘米。
故答案为:B
【点睛】由题意发现长方形的长乘就是圆的周长是解题的关键。
7. 1 ab
【分析】a-b=1,(a、b均为非零自然数),由此可知,a和b是相邻的两个数,即a和b是互质数,如果两个数为互质数,最大公因数是1,最小公倍数是两个数的乘积,据次解答。
【详解】根据分析可知,a与b是互质数,a和b的最大公因数是1,最小公倍数是ab。
如果a-b=1(a、b均为非零自然数),那么a与b的最大公因数是1,最小公倍数是ab。
【点睛】熟练掌握求两个数的最小公倍数和最大公因数的方法是解答本题的关键。
8. 8 0
【分析】既是2的倍数又是3的倍数的数的特征:个位上是0、2、4、6或8,且各个数位上的数字之和是3的倍数;既是3的倍数又是5的倍数的数的特征:个位上是0或5,且各个数位上的数字之和是3的倍数;依据此特征分析并填空即可。
【详解】25既是2的倍数又是3的倍数,则个位上是0、2、4、6或8,求里最大填几,从8开始试,2+5+8=15,15是3的倍数,那么258既是2的倍数又是3的倍数,即里最大填8;45既是3的倍数又是5的倍数,则个位上是0或5,4+5+0=9,9是3的倍数,4+5+5=14,14不是3的倍数,那么450既是3的倍数又是5的倍数,即里可以填0。
【点睛】此题重点考查2、5、3倍数的特征及灵活运用。
9. 2 25
【分析】根据分数的基本性质:分数的分子分母同时乘或除以一个不为0的数,分数的大小不边;的分子除以2,则分母也除以2;的分母加上40,得到的和再除以分母,求出分母扩大到原来的多少倍,分子也扩大到原来的多少倍,再用扩大后的分子减去原来的分子,即可解答。
【详解】的分子除以2,要使分数的大小不变,分母应除以2;
(8+40)÷8
=48÷8
=6
5×6-5
=30-5
=25
的分子除以2,要使分数的大小不变,分母应除以2;的分母加上40,要使分数的大小不变,分子应加上25。
【点睛】熟练掌握分数的基本性质是解答本题的关键。
10. 25.12 50.24
【分析】画圆时,圆规两脚间的距离即为半径长度,根据圆的周长公式:C=2r,圆的面积公式:S=r2,将数值代入计算即可。
【详解】由分析可得:
2×3.14×4
=6.28×4
=25.12(cm)
3.14×42
=3.14×16
=50.24(cm2)
综上所述:圆规两脚之间的距离是4cm,画出圆的周长是25.12cm,面积是50.24cm2。
【点睛】本题考查了用圆规画圆,圆规两脚之间的距离就是要画的圆的半径,同时需要牢记圆的周长和面积公式。
11. 奇数 偶数
【分析】奇数+奇数=偶数;奇数+偶数=奇数;偶数+偶数=偶数;奇数个奇数相加,和是奇数;偶数个奇数相加,和是偶数;第一空据此解答;
奇数×奇数=奇数;奇数×偶数=偶数;偶数×偶数=偶数;第二小空据此解答。
【详解】3+5+7+…+17+19是9个奇数相加,和是奇数;
2×19×23×37×111×239,2是偶数,19、23、37、111、239是奇数,2×19×23×37×111×239积是偶数。
的和是奇数;的积是偶数。
【点睛】熟练掌握运算性质(奇数和偶数)是解答本题的关键,
12.(1) 32 24
(2)72
【分析】(1)根据图可知,a对应的是8秒的时候,由于当P在AB段上移动时,P、A、B不能构成三角形,所以没有面积,即在第4秒的时候,开始有面积,说明第4秒走到了B点,那么AB的长度是:4×2=8(厘米),当P点走到C点的时候,三角形的面积是最大的,则此时走了10秒,当第8秒时,即在BC段走了4秒,那么此时的PB长是:4×2=8(厘米),高是AB的长度,根据三角形的面积公式:底×高÷2,即8×8÷2,即可求出a的值;当在10秒开始,三角形的面积下降,此时在CD线上,由于在15秒时,下降趋势变化,说明15秒时走到了D点,从D点到A点总共走了3秒,即AD的长度是3×2=6(厘米),高是AB的长度,即此时的c表示的数是:6×8÷2,据此即可求解;
(2)由于AD是6厘米,AB是8厘米,BC总共走了10-4=6(秒),即BC的长度是:6×2=12(厘米),根据梯形的面积公式:(上底+下底)×高÷2,把数代入即可求解。
【详解】(1)4×2=8(厘米)
(8-4)×2
=4×2
=8(厘米)
8×8÷2=32(平方厘米)
18-15=3(秒)
3×2=6(厘米)
6×8÷2=24(平方厘米)
图2中的a是32平方厘米,c是24平方厘米。
(2)10-4=6(秒)
6×2=12(厘米)
(6+12)×8÷2
=18×8÷2
=72(平方厘米)
图1中梯形ABCD的面积是72平方厘米。
【点睛】本题主要考查折线统计图的分析以及三角形和梯形的面积公式,关键是找准三角形的底和高的变化是解题的关键。
13.正确
【详解】同一个圆中,圆心角越小,扇形也越小.原题说法正确.故答案为正确.
14.
【详解】略
15.√
【详解】略
16.×
【分析】等式两边同时乘或除以同一个不是0的数,所得结果仍然是等式,这是等式的性质。由此计算出n的值即可。
【详解】0.9n÷4=18
0.9n÷4×4=18×4
0.9n=72
0.9n÷0.9=72÷0.9
n=80
0.9n÷4=18的解是n=80。原题说法错误。
故答案为:×
17.√
【分析】根据最简分数的含义进行分析,分子和分母只有公因数1,像这样的分数叫作最简分数。
【详解】如果一个分数的分子和分母的最大公因数是1,即分子和分母只有公因数1,那么这个分数就是最简分数。例如:,7和8的最大公因数是1,它是最简分数。说法正确。
故答案为:√
18.900;;;;
0.04;;;0
【详解】略
19.;3;
【分析】先通分再从左到右依次计算即可;
根据减法的性质进行简算;
原式化为:1-(1-)-(-)-(-)-(-)-(-),再根据减法的性质进行简算即可。
【详解】-+
=-+
=
5--
=5-(+)
=5-2
=3
1-----
=1-(1-)-(-)-(-)-(-)-(-)
=1-1+-+-+-+-+
=
20.x=2.5;x=2.4;x=5
【分析】合并方程左边同类项,再根据等式的性质2,方程的两边同时除以(24+38)即可;
根据等式的性质1,方程的两边同时加上0.5×8,再根据等式的性质2,方程的两边同时除以2.5即可;
根据等式的性质2,方程的两边同时除以2.4即可。
【详解】
解:(24+38)x=155
x=155÷62
x=2.5
解:2.5x=2+4
x=6÷2.5
x=2.4
解:x=12÷2.4
x=5
21.(1)10.75平方厘米(2)87.92平方厘米
【分析】(1)空白部分可以组成一个半圆,用长方形的面积减去半圆的面积即是阴影部分的面积。长方形的面积=长×宽,圆的面积=πr2,据此解答。要注意长方形的宽等于半圆的半径,是10÷2=5(厘米)。
(2)圆环的面积=π(R2-r2),据此解答。
【详解】(1)10÷2=5(厘米)
10×5-3.14×52÷2
=50-39.25
=10.75(平方厘米)
(2)3.14×(82-62)
=3.14×28
=87.92(平方厘米)
22.8.8米;4.8米
【分析】设较短的一根绳长x米,则较长的一根绳长(2x-0.8),两根绳长加起来共13.6米,根据这个等量关系列方程解答。
【详解】解:设较短的一根绳长x米。
x+(2x-0.8)=13.6
3x-0.8+0.8=13.6+0.8
3x÷3=14.4÷3
x=4.8
当x=4.8时,
2x-0.8
=2×4.8-0.8
=8.8(米)
答:较长的一根长8.8米,较短的一根长4.8米。
【点睛】解答本题还可以先用13.6米加上0.8米,再除以3,求出较短的绳长,进而求出较长的绳长。
23.40千米
【分析】设乙每小时行x千米,则甲每小时行(x+0.5)千米。根据题意,(甲的速度+乙的速度)×行驶时间+两车相距的路程=总路程,据此列方程即可解答。
【详解】解:设乙每小时行x千米。
(x+0.5+x)×4.2+28.9=367
(2x+0.5)×4.2+28.9=367
(2x+0.5)×4.2=367-28.9
(2x+0.5)×4.2=338.1
2x+0.5=338.1÷4.2
2x+0.5=80.5
2x=80.5-0.5
2x=80
x=80÷2
x=40
答:乙每小时行40千米。
【点睛】本题考查相遇问题。列方程解含有两个未知数的问题时,设其中的一个未知数是x,用含有x的式子表示另一个未知数,再根据等量关系即可列出方程。找出本题的等量关系式是解题的关键。
24.8天;160个
【分析】设计划吃x天,由“每天吃4个,则多长48个苹果”,可知苹果个数为4x+48个;由“每天吃6个,则又少8个苹果”可知,苹果个数为6x-8个;因为苹果个数相等,列方程:4x+48=6x-8,解方程,求出计划吃的天数,进而求出妈妈买回苹果的个数。
【详解】解:设计划吃x天。
4x+48=6x-8
6x-4x=48+8
2x=56
x=56÷2
x=28
4×28+48
=112+48
=160(个)
答:计划吃28天,妈妈买回苹果160个。
【点睛】本题考查方程的实际应用,根据苹果吃的天数和苹果的个数,设出未知数,找出相关的量,列方程,解方程。
25.113.04平方米
【分析】根据题意可知小路的内圆半径是8米,则外面半径是(8+2)米,根据圆环的面积公式:S=π(R2-r2),求出小路的面积即可。
【详解】8+2=10(米)
3.14×(102-82)
=3.14×(100-64)
=3.14×36
=113.04(平方米)
答:这条小路的面积是113.04平方米。
【点睛】本题考查的是圆环的面积公式的应用,明确大圆和小圆的半径是解题的关键。
26.①见详解
②2020;2017
③2020;2018~2019
【分析】①结合表格的数据,在统计图中描出每个商场营业额数据的点,然后再连线即可;
②将万福商场的各年份的营业额排序,找出最多与最少的数值即可;
③将东方商场的各年份的营业额排序,找出最多的数值;每两年之间的差额越大,营业额增长也就越快;
【详解】①
②60>55>50>45,所以万福商场在(2020)年营业额最多,在(2017)年营业额最少。
③80>65>40>35,
40-35=5(万元),65-40=25(万元),80-65=15(万元)
所以,东方商场在(2020)年营业额最多,(2018~2019)年营业额增长最快。
【点睛】此题考查了复式折线统计图的内容,关键能够根据图标获取正确的信息。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
