函数的单调性(1)(2)

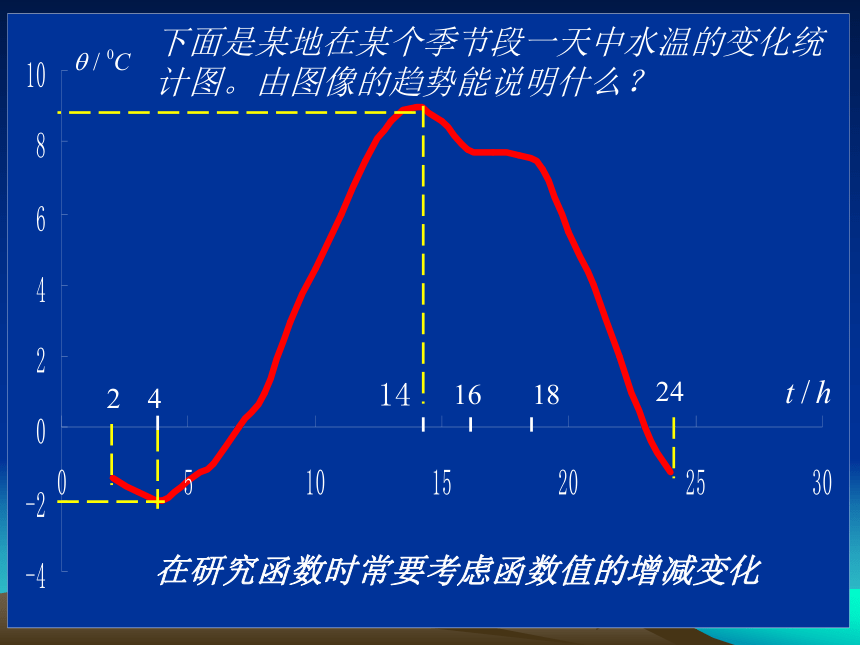
课件22张PPT。414161824在研究函数时常要考虑函数值的增减变化下面是某地在某个季节段一天中水温的变化统计图。由图像的趋势能说明什么？2函数的单调性1制作人
贾永宏 则称函数f (x)在此区间上是增加的(或递增的)。
称此区间为单调(增)区间。如何用x与 f(x)来描述上升的图象？如何用x与 f(x)来描述下降的图象？ 则称函数f (x)在此区间上是减少的(或递减的)。
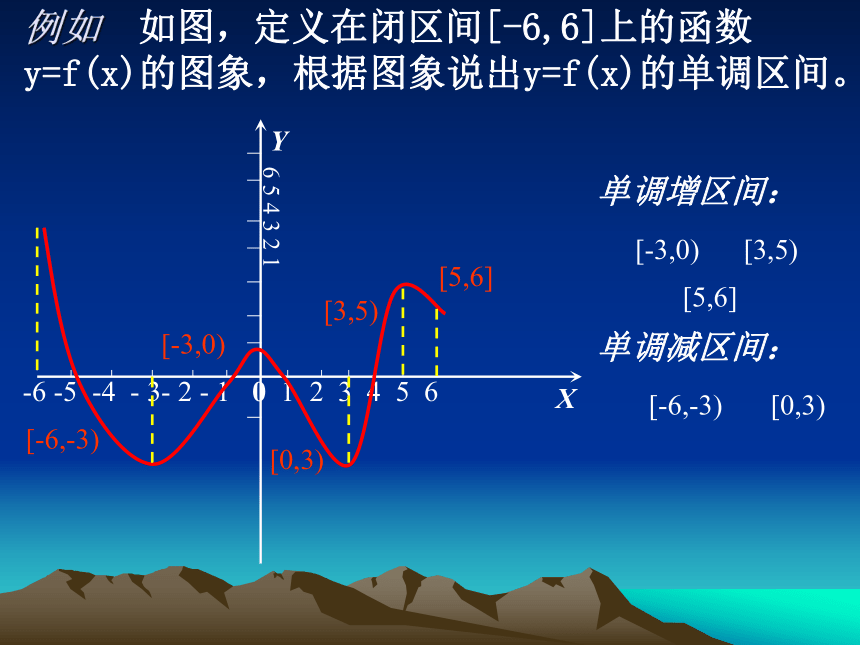
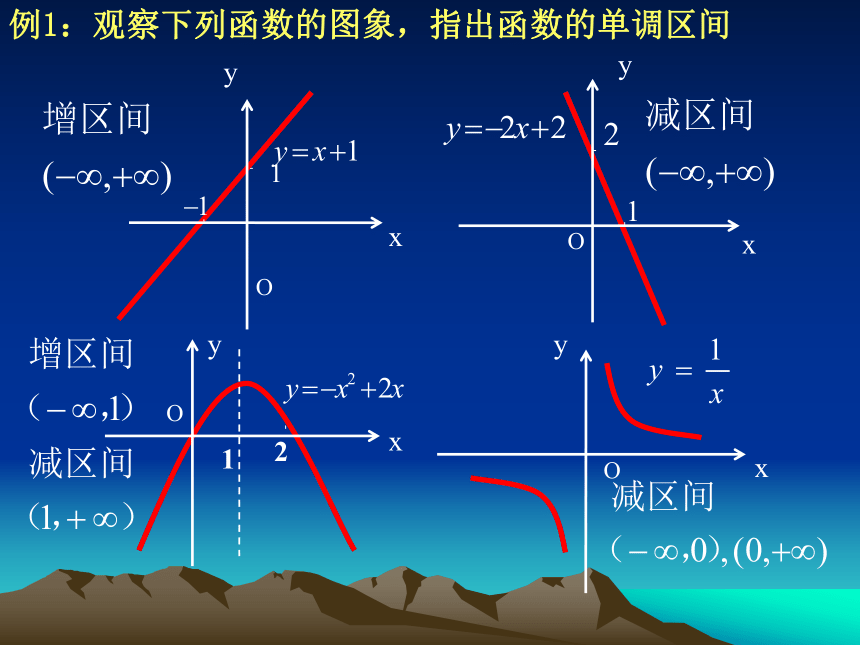
称此区间为单调(减)区间。OxyY X -6 -5 -4 - 3- 2 - 1 0 1 2 3 4 5 6 6 5 4 3 2 1 例如 如图，定义在闭区间[-6,6]上的函数 y=f(x)的图象，根据图象说出y=f(x)的单调区间。[-6,-3)[-6,-3)[-3,0)[0,3)[3,5)[5,6][-3,0)[0,3)[3,5)[5,6]单调增区间：单调减区间：函数单调性的概念： 若对于A内的任意那么就说y=f(x)在数集A上是增加的。1.一般地，对于函数y=f(x)定义域内的一个子集A 类似地,若对于A内的任意那么就说y=f(x)在数集A上是减少的。2.若函数y=f(x)在定义域的某个子集上是增加的或是减少的,则称y=f(x)在这个子集上具有单调性。3.若函数y=f(x)在整个定义域上是增加的或是减少的,则分别称此函数为增函数或减函数，统称为单调函数。OxyOxyO2yOx例1：观察下列函数的图象，指出函数的单调区间要注意的是：
1.函数的单调性是相对其定义域的某个区间而言的，是函数的局部性质而不是整体性质。如： 2.函数的单调区间是否包含端点不影响其单调性如:
函数 的单调区间 也可
写成 例 2 证明函数f(x) = 3x + 2 在R上是增函数. 证明：设 X1 , X2是 R 上的任意两个实数，且X1 < X2，则f(X1) - f(X2)=(3X1+2) - (3X2 +2)= 3(X1-X2).由X1 < X2，得X1-X2 < 0 ,于是f(X1)-f(X2) < 0 ,即f(X1) < f(X2) 所以，f(x) = 3x + 2 在 R 上 是 增 函 数（1）取值 （2）作差（3）判断（4）结论单调递增区间：单调递减区间：xy21o练习：D13小结函数的单调性定义
单调区间，增函数和减函数单调函数概念
求某个函数的单调区间，讨论其单调性
证明函数在给定区间上具有单调性的步骤
（1）取值（自变量）
（2）作差变形（函数值）
（3）判断符号（差）
（4）下结论作业函数的单调性2制作人
贾永宏复习提问１、函数单调性的定义？
2 、函数单调性的证明步骤
本节我们利用函数单调性求最值和参数的范围例3.f(x)是二次函数，且在 x=1处取得最值，f( )又 可得 f(x)在 上单调递增， 二次函数的图像开口向上，f(x)在
上单调递减。
由于0与2关于 x=1对称， f(2)=f(0).
-2 < 0 , f(-2)>f(0), 即 f(-2)>f(2)ox=12-2xy由单调性知 f(x)max=f(-2)
f(x)min=f(1)例4.求函数 的最小值。解法一：定义域为 ，易证得函数f(x)在其定义域上单调递增（4步略）， f(x)min= f(1) =1 解法二：定义域为 ，令 otg(t)1-1由于g(t)的对称轴 在 的
左 侧， g(t)的开口向上，如图所示。
函数在 上单调递增，当t=0
时,g(t)min=1, f(x)的最小值为1.例5.（1）若函数 在区间
上是减函数，求实数a的取值范围；
（2） 上单调递减，求实数
k 的取值范围。解：(1) , 其对称轴为x=1-a,若要二次函数在 上单调递减，必须满足o1-a4xy例5.（1）若函数 在区间
上是减函数，求实数a的取值范围；
（2） 上单调递减，求实数
k 的取值范围。解（2）当k=0时 ， 满足题意；
当k>0时,抛物线开口向上，在 上不可能单调递减；
当 k<0时，对称轴 上单调递减。
综上， .练习小结作业