第一章 三角形 5 利用三角形全等测距离
文档属性
| 名称 | 第一章 三角形 5 利用三角形全等测距离 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-28 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第一章 三角形
5 利用三角形全等测距离
列清单·划重点
知识点 利用三角形全等测距离
利用三角形全等测距离实际上就是利用已有的全等三角形,或构造出全等三角形,通过全等三角形的对应边相等这一性质,把较难测量的距离转化为____________线段的长度或较容易测量的____________,从而得出要测线段的长.
明考点·识方法
考点 利用三角形全等测距离
典例 如图所示,A,B两个建筑物分别位于河的两岸,要测得它们之间的距离,可以从B出发沿河岸画一条射线BF,在 BF上截取BC=CD,过 D 作DE∥AB,使 E,C,A在同一条直线上,则 DE 的长就是A,B 之间的距离.请说明理由.
思路导析 因为 DE∥AB,所以∠A=∠E,∠B=∠CDE.又因为 BC=CD,所以△ABC≌△EDC,可得AB=DE.
变式 在新修的花园小区中,有一条“Z”字形绿色长廊 ABCD(如图所示),其中AB∥CD,在 AB,BC,CD三段绿色长廊上各修建一凉亭E,M,F,且M是BC 的中点,在凉亭 M与F 之间有一池塘,不能直接到达,要想知道M与F 的距离,要测出的长度是( )
A. EM B. BE C. CF D. CM
当堂测·夯基础
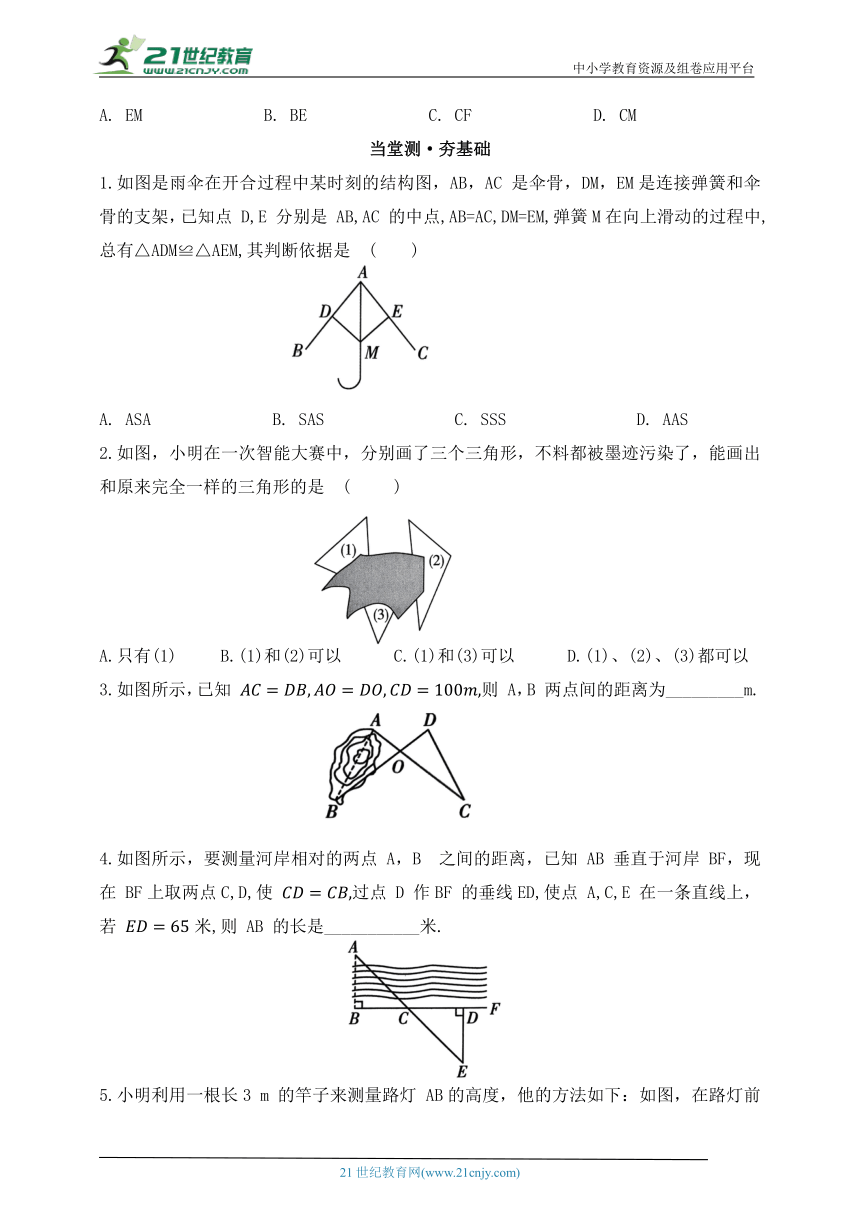
1.如图是雨伞在开合过程中某时刻的结构图,AB,AC 是伞骨,DM,EM是连接弹簧和伞骨的支架,已知点 D,E 分别是 AB,AC 的中点,AB=AC,DM=EM,弹簧M在向上滑动的过程中,总有△ADM≌△AEM,其判断依据是 ( )
A. ASA B. SAS C. SSS D. AAS
2.如图,小明在一次智能大赛中,分别画了三个三角形,不料都被墨迹污染了,能画出和原来完全一样的三角形的是 ( )
A.只有(1) B.(1)和(2)可以 C.(1)和(3)可以 D.(1)、(2)、(3)都可以
3.如图所示,已知 则 A,B 两点间的距离为_________m.
4.如图所示,要测量河岸相对的两点 A,B 之间的距离,已知 AB 垂直于河岸 BF,现在 BF上取两点C,D,使 过点 D 作BF 的垂线ED,使点 A,C,E 在一条直线上,若 米,则 AB 的长是___________米.
5.小明利用一根长3 m 的竿子来测量路灯 AB的高度,他的方法如下:如图,在路灯前选一点 P,使并测得 然后把竖直的竿子( 在 BP 的延长线上左右移动,使 此时测得请根据这些数据,计算出路灯 AB 的高度.
参考答案
【列清单·划重点】
知识点 已知 距离
【明考点·识方法】
典例 解:因为 ∥(作图),
所以 (两直线平行,内错角相等).
又因为(已知),所以
所以 (全等三角形的对应边相等).
变式 A
【当堂测·夯基础】
1. C 2. B 3.100 4.65
5.解:因为∠CPD = 20°,∠APB = 70°,∠CDP=∠ABP=90°,
所以∠PCD=∠APB=70°.
在△CPD和△PAB中,
所以△CPD≌△PAB(ASA).所以 DP=AB.
因为 BD=11.2m,BP=3 m.所以 DP=BD-BP=8.2(m),即 AB=8.2m .
答:路灯 AB的高度是 8.2m .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第一章 三角形
5 利用三角形全等测距离
列清单·划重点
知识点 利用三角形全等测距离
利用三角形全等测距离实际上就是利用已有的全等三角形,或构造出全等三角形,通过全等三角形的对应边相等这一性质,把较难测量的距离转化为____________线段的长度或较容易测量的____________,从而得出要测线段的长.
明考点·识方法
考点 利用三角形全等测距离
典例 如图所示,A,B两个建筑物分别位于河的两岸,要测得它们之间的距离,可以从B出发沿河岸画一条射线BF,在 BF上截取BC=CD,过 D 作DE∥AB,使 E,C,A在同一条直线上,则 DE 的长就是A,B 之间的距离.请说明理由.
思路导析 因为 DE∥AB,所以∠A=∠E,∠B=∠CDE.又因为 BC=CD,所以△ABC≌△EDC,可得AB=DE.
变式 在新修的花园小区中,有一条“Z”字形绿色长廊 ABCD(如图所示),其中AB∥CD,在 AB,BC,CD三段绿色长廊上各修建一凉亭E,M,F,且M是BC 的中点,在凉亭 M与F 之间有一池塘,不能直接到达,要想知道M与F 的距离,要测出的长度是( )
A. EM B. BE C. CF D. CM
当堂测·夯基础
1.如图是雨伞在开合过程中某时刻的结构图,AB,AC 是伞骨,DM,EM是连接弹簧和伞骨的支架,已知点 D,E 分别是 AB,AC 的中点,AB=AC,DM=EM,弹簧M在向上滑动的过程中,总有△ADM≌△AEM,其判断依据是 ( )
A. ASA B. SAS C. SSS D. AAS
2.如图,小明在一次智能大赛中,分别画了三个三角形,不料都被墨迹污染了,能画出和原来完全一样的三角形的是 ( )
A.只有(1) B.(1)和(2)可以 C.(1)和(3)可以 D.(1)、(2)、(3)都可以
3.如图所示,已知 则 A,B 两点间的距离为_________m.
4.如图所示,要测量河岸相对的两点 A,B 之间的距离,已知 AB 垂直于河岸 BF,现在 BF上取两点C,D,使 过点 D 作BF 的垂线ED,使点 A,C,E 在一条直线上,若 米,则 AB 的长是___________米.
5.小明利用一根长3 m 的竿子来测量路灯 AB的高度,他的方法如下:如图,在路灯前选一点 P,使并测得 然后把竖直的竿子( 在 BP 的延长线上左右移动,使 此时测得请根据这些数据,计算出路灯 AB 的高度.
参考答案
【列清单·划重点】
知识点 已知 距离
【明考点·识方法】
典例 解:因为 ∥(作图),
所以 (两直线平行,内错角相等).
又因为(已知),所以
所以 (全等三角形的对应边相等).
变式 A
【当堂测·夯基础】
1. C 2. B 3.100 4.65
5.解:因为∠CPD = 20°,∠APB = 70°,∠CDP=∠ABP=90°,
所以∠PCD=∠APB=70°.
在△CPD和△PAB中,
所以△CPD≌△PAB(ASA).所以 DP=AB.
因为 BD=11.2m,BP=3 m.所以 DP=BD-BP=8.2(m),即 AB=8.2m .
答:路灯 AB的高度是 8.2m .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
