第一章 三角形 3 探索三角形全等的条件 第2课时 “角边角”和“角角边”
文档属性
| 名称 | 第一章 三角形 3 探索三角形全等的条件 第2课时 “角边角”和“角角边” |
|
|
| 格式 | docx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-28 19:25:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第一章 三角形
3 探索三角形全等的条件
第2课时 “角边角”和“角角边”
列清单·划重点
知识点① “角边角”
两角及其_______分别相等的两个三角形全等,简写成“角边角”或“ASA”.
知识点② “角角边”
两角分别相等且其中一组等角的__________相等的两个三角形全等,简写为“角角边”或“AAS”.
明考点·识方法
考点① “角边角”的应用
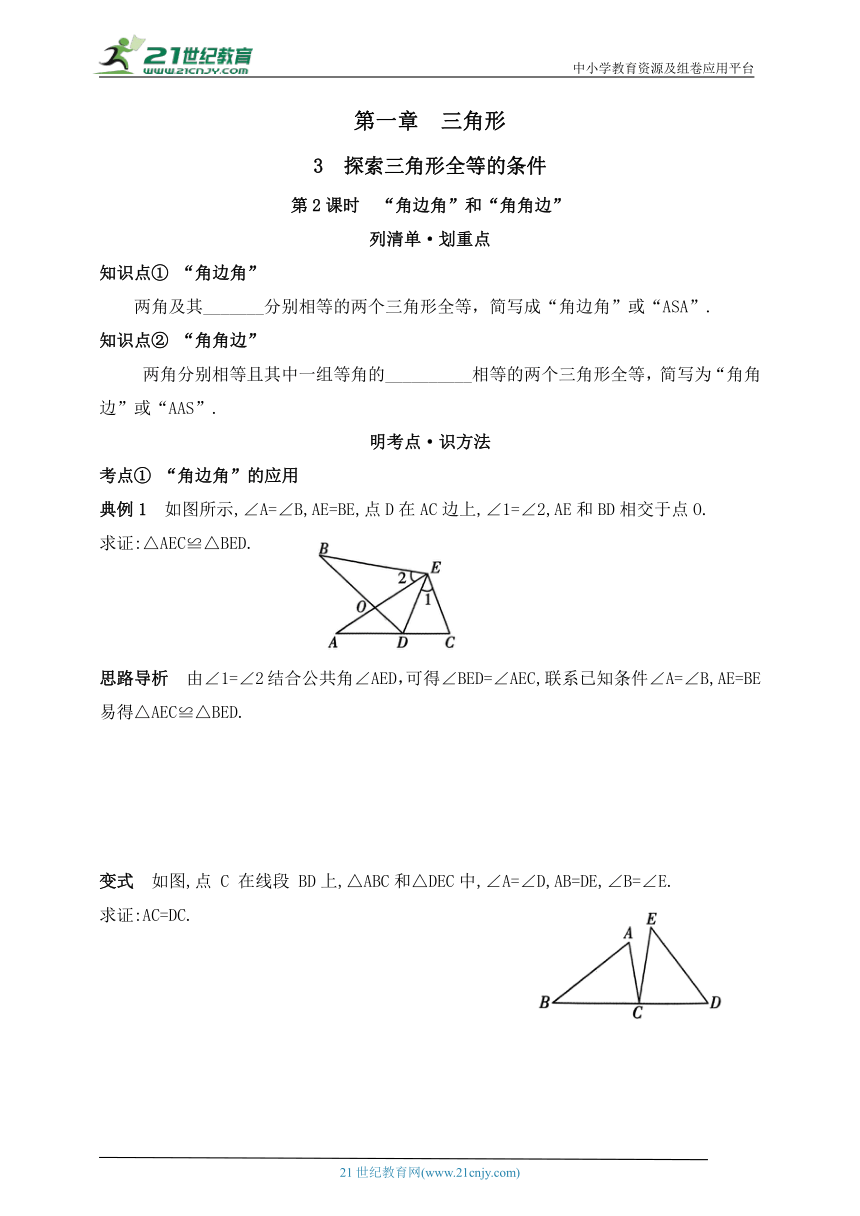
典例1 如图所示,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
求证:△AEC≌△BED.
思路导析 由∠1=∠2结合公共角∠AED,可得∠BED=∠AEC,联系已知条件∠A=∠B,AE=BE
易得△AEC≌△BED.
变式 如图,点 C 在线段 BD上,△ABC和△DEC中,∠A=∠D,AB=DE,∠B=∠E.
求证:AC=DC.
考点② “角角边”的应用
典例 2 如图所示,在△ABC中,∠B=∠C,过BC的中点D作DE⊥AB,DF⊥AC,垂足分别为点E,F.
(1)求证:DE=DF;
(2)若∠BDE=40°,求∠BAC的度数.
思路导析 (1)由垂直和∠B=∠C 以及中点,可得出△BED≌△CFD,从而证明 DE=DF;(2)在△BED中,由三角形内角和定理可得∠B=50°,从而∠C=50°;再在△ABC中,由三角形内角和定理可得∠BAC=80°.
方法技巧
证明三角形全等寻找角相等常用的方法:
(1)公共角相等、对顶角相等、直角相等;
(2)等角加(减)等角,其和(差)相等;
(3)同角或等角的余(补)角相等;
(4)根据角平分线、平行线得角相等.
变式 如图所示,∠1=∠2,∠C=∠D,若∠CAE=85°,则∠DBE的度数是 ( )
A.80° B.85° C.90° D.95°
当堂测·夯基础
1.如图所示,点 B,F,C,E 共线, ∥若 则DE长度为 ( )
A.7 cm B.14 cm C.3.5cm D.21 cm
第1题图 第2题图
2.如图,已知太阳光线 AC 和 DE 是平行的,在同一时刻两根高度相同的木杆竖直插在地面上,在太阳光照射下,其影子一样长.这里判断影长相等利用了全等图形的性质,其中判断 的依据是_____________.
3.如图所示,在△ABC 中,已知∠1=∠2,BE= CD,AB =5,AE= 2,则 CE=__________.
第3题图 第4题图
4.如图,∠1=∠2,若要证明 需要补充的一个条件是______________.(写出一个即可)
5.如图,已知 AB 与CD 相交于点O,AC∥BD,AO=BO.求证:AC=BD.
参考答案
【列清单·划重点】
知识点 1 夹边
知识点 2 对边
【明考点·识方法】
典例 1 证明:因为∠1=∠2,所以∠1+∠AED=∠2+∠AED,即∠AEC=∠BED.
在△AEC和△BED中, 所以△AEC≌△BED(ASA).
变式 证明:在△ABC和△DEC中,
所以△ABC≌△DEC(ASA),所以AC=DC.
典例2 解:(1)证明:因为 DE⊥AB,DF⊥AC,所以∠BED=∠CFD=90°.
因为 D 是 BC 的中点,所以 BD=CD.
在△BED与△CFD中,
所以△BED≌△CFD(AAS),所以DE=DF;
(2)因为∠BDE=40°,所以∠B=50°,所以∠C=∠B=50°,
所以∠BAC=180°-∠B-∠C=180°-50°-50°=80°.
变式 D
【当堂测·夯基础】
1. A 2.“AAS” 3.3
4. BC=DE(答案不唯一)
5.证明:因为AC∥BD,所以∠A=∠B,∠C=∠D,
在△AOC和△BOD中,
所以△AOC≌△BOD(AAS),所以AC=BD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第一章 三角形
3 探索三角形全等的条件
第2课时 “角边角”和“角角边”
列清单·划重点
知识点① “角边角”
两角及其_______分别相等的两个三角形全等,简写成“角边角”或“ASA”.
知识点② “角角边”
两角分别相等且其中一组等角的__________相等的两个三角形全等,简写为“角角边”或“AAS”.
明考点·识方法
考点① “角边角”的应用
典例1 如图所示,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
求证:△AEC≌△BED.
思路导析 由∠1=∠2结合公共角∠AED,可得∠BED=∠AEC,联系已知条件∠A=∠B,AE=BE
易得△AEC≌△BED.
变式 如图,点 C 在线段 BD上,△ABC和△DEC中,∠A=∠D,AB=DE,∠B=∠E.
求证:AC=DC.
考点② “角角边”的应用
典例 2 如图所示,在△ABC中,∠B=∠C,过BC的中点D作DE⊥AB,DF⊥AC,垂足分别为点E,F.
(1)求证:DE=DF;
(2)若∠BDE=40°,求∠BAC的度数.
思路导析 (1)由垂直和∠B=∠C 以及中点,可得出△BED≌△CFD,从而证明 DE=DF;(2)在△BED中,由三角形内角和定理可得∠B=50°,从而∠C=50°;再在△ABC中,由三角形内角和定理可得∠BAC=80°.
方法技巧
证明三角形全等寻找角相等常用的方法:
(1)公共角相等、对顶角相等、直角相等;
(2)等角加(减)等角,其和(差)相等;
(3)同角或等角的余(补)角相等;
(4)根据角平分线、平行线得角相等.
变式 如图所示,∠1=∠2,∠C=∠D,若∠CAE=85°,则∠DBE的度数是 ( )
A.80° B.85° C.90° D.95°
当堂测·夯基础
1.如图所示,点 B,F,C,E 共线, ∥若 则DE长度为 ( )
A.7 cm B.14 cm C.3.5cm D.21 cm
第1题图 第2题图
2.如图,已知太阳光线 AC 和 DE 是平行的,在同一时刻两根高度相同的木杆竖直插在地面上,在太阳光照射下,其影子一样长.这里判断影长相等利用了全等图形的性质,其中判断 的依据是_____________.
3.如图所示,在△ABC 中,已知∠1=∠2,BE= CD,AB =5,AE= 2,则 CE=__________.
第3题图 第4题图
4.如图,∠1=∠2,若要证明 需要补充的一个条件是______________.(写出一个即可)
5.如图,已知 AB 与CD 相交于点O,AC∥BD,AO=BO.求证:AC=BD.
参考答案
【列清单·划重点】
知识点 1 夹边
知识点 2 对边
【明考点·识方法】
典例 1 证明:因为∠1=∠2,所以∠1+∠AED=∠2+∠AED,即∠AEC=∠BED.
在△AEC和△BED中, 所以△AEC≌△BED(ASA).
变式 证明:在△ABC和△DEC中,
所以△ABC≌△DEC(ASA),所以AC=DC.
典例2 解:(1)证明:因为 DE⊥AB,DF⊥AC,所以∠BED=∠CFD=90°.
因为 D 是 BC 的中点,所以 BD=CD.
在△BED与△CFD中,
所以△BED≌△CFD(AAS),所以DE=DF;
(2)因为∠BDE=40°,所以∠B=50°,所以∠C=∠B=50°,
所以∠BAC=180°-∠B-∠C=180°-50°-50°=80°.
变式 D
【当堂测·夯基础】
1. A 2.“AAS” 3.3
4. BC=DE(答案不唯一)
5.证明:因为AC∥BD,所以∠A=∠B,∠C=∠D,
在△AOC和△BOD中,
所以△AOC≌△BOD(AAS),所以AC=BD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
