第一章 三角形 3 探索三角形全等的条件 第3课时 “边角边”
文档属性
| 名称 | 第一章 三角形 3 探索三角形全等的条件 第3课时 “边角边” |  | |
| 格式 | docx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-28 19:26:42 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第一章 三角形
3 探索三角形全等的条件
第3课时 “边角边”
列清单·划重点
知识点 “边角边”
两边及其_________分别相等的两个三角形全等,简写成“边角边”或“SAS”.
注意
全等三角形对应角的平分线相等,对应中线相等,对应高相等.
明考点·识方法
考点 “边角边”的应用
典例 如图,AC是四边形ABCD的对角线,∠1=∠B ,点 E,F分别在 AB,BC上,BE=CD,BF=CA,连接EF.
(1)求证:
(2)若 ∥求 的度数.
思路导析 (1)要证明∠D=∠2,可通过证明△BEF≌△CDA得到,根据题目给出的条件可由SAS判定全等;(2)先求出∠2=78°,又由EF∥AC,可得∠BAC=∠2=78°.
变式 下列各图中,a,b,c为三角形的边长,则甲、乙、丙三个三角形和左侧 全等的是 ( )
A.甲和乙 B.乙和丙 C.甲和丙 D.只有丙
当堂测·夯基础
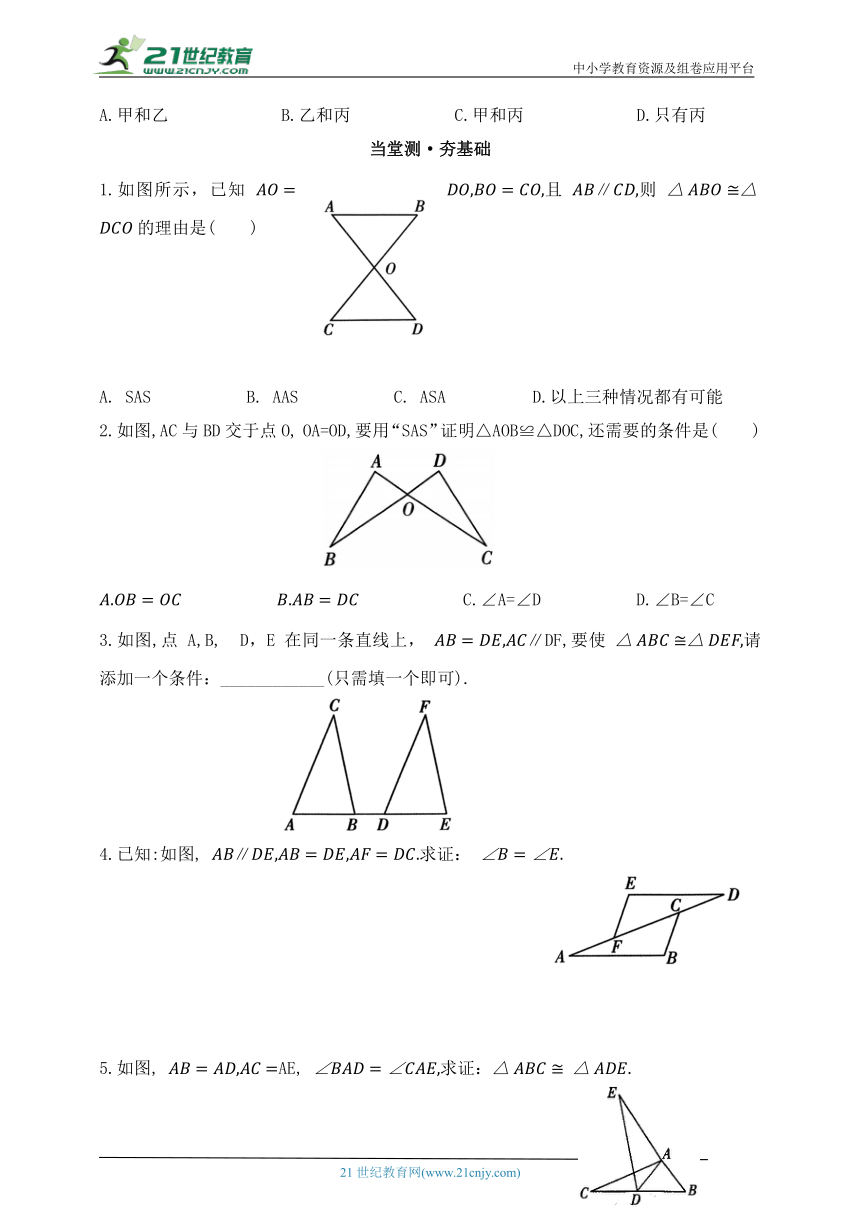
1.如图所示,已知 且 ∥则 的理由是( )
A. SAS B. AAS C. ASA D.以上三种情况都有可能
2.如图,AC与BD交于点O, OA=OD,要用“SAS”证明△AOB≌△DOC,还需要的条件是( )
C.∠A=∠D D.∠B=∠C
3.如图,点 A,B, D,E 在同一条直线上, ∥DF,要使 请添加一个条件:____________(只需填一个即可).
4.已知:如图, ∥求证:
5.如图, AE, 求证:
参考答案
【列清单·划重点】
知识点 夹角
【明考点·识方法】
典例1 解:(1)证明:在△BEF 和△CDA中,
所以△BEF≌△CDA(SAS),所以∠D=∠2;
(2)因为∠D=∠2,所以∠2=78°.
因为 EF∥AC,所以∠BAC=∠2=78°.
变式 B
【当堂测·夯基础】
1. D 2. A
3. AC=DF(答案不唯一)
4.证明:因为AB∥DE,所以∠A=∠D,
因为AF=DC,所以 AF+CF=DC+CF,即 AC=DF.
在△ABC与△DEF中,
所以△ABC≌△DEF(SAS),所以∠B=∠E.
5.证明:因为∠BAD=∠CAE,
所以∠BAD +∠CAD =∠CAE +∠CAD,即∠BAC=∠DAE,
在△ABC和△ADE中,
所以△ABC≌△ADE(SAS).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第一章 三角形
3 探索三角形全等的条件
第3课时 “边角边”
列清单·划重点
知识点 “边角边”
两边及其_________分别相等的两个三角形全等,简写成“边角边”或“SAS”.
注意
全等三角形对应角的平分线相等,对应中线相等,对应高相等.
明考点·识方法
考点 “边角边”的应用
典例 如图,AC是四边形ABCD的对角线,∠1=∠B ,点 E,F分别在 AB,BC上,BE=CD,BF=CA,连接EF.
(1)求证:
(2)若 ∥求 的度数.
思路导析 (1)要证明∠D=∠2,可通过证明△BEF≌△CDA得到,根据题目给出的条件可由SAS判定全等;(2)先求出∠2=78°,又由EF∥AC,可得∠BAC=∠2=78°.
变式 下列各图中,a,b,c为三角形的边长,则甲、乙、丙三个三角形和左侧 全等的是 ( )
A.甲和乙 B.乙和丙 C.甲和丙 D.只有丙
当堂测·夯基础
1.如图所示,已知 且 ∥则 的理由是( )
A. SAS B. AAS C. ASA D.以上三种情况都有可能
2.如图,AC与BD交于点O, OA=OD,要用“SAS”证明△AOB≌△DOC,还需要的条件是( )
C.∠A=∠D D.∠B=∠C
3.如图,点 A,B, D,E 在同一条直线上, ∥DF,要使 请添加一个条件:____________(只需填一个即可).
4.已知:如图, ∥求证:
5.如图, AE, 求证:
参考答案
【列清单·划重点】
知识点 夹角
【明考点·识方法】
典例1 解:(1)证明:在△BEF 和△CDA中,
所以△BEF≌△CDA(SAS),所以∠D=∠2;
(2)因为∠D=∠2,所以∠2=78°.
因为 EF∥AC,所以∠BAC=∠2=78°.
变式 B
【当堂测·夯基础】
1. D 2. A
3. AC=DF(答案不唯一)
4.证明:因为AB∥DE,所以∠A=∠D,
因为AF=DC,所以 AF+CF=DC+CF,即 AC=DF.
在△ABC与△DEF中,
所以△ABC≌△DEF(SAS),所以∠B=∠E.
5.证明:因为∠BAD=∠CAE,
所以∠BAD +∠CAD =∠CAE +∠CAD,即∠BAC=∠DAE,
在△ABC和△ADE中,
所以△ABC≌△ADE(SAS).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
