人教版九年级上册数学第二十二章二次函数应用题专题训练(含解析)
文档属性
| 名称 | 人教版九年级上册数学第二十二章二次函数应用题专题训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-28 20:03:17 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
人教版九年级上册数学第二十二章 二次函数应用题专题训练
1.某水果超市经销一种水果,售价每千克元.每千克盈利元,每天可售出千克,调查发现,进货价不变的情况下,每千克涨价元,日销售量将减少千克.规定每千克涨价不能超过元.
(1)该超市希望每天盈利元,那么每千克应涨价多少元?
(2)超市决定每卖出千克捐赠元()给贫困山区学生,若每天盈利随着售价的增加而增大,求的取值范围.
2.小莹妈妈的花卉超市以15元/盆的价格新购进了某种盆栽花卉,为了确定售价,小莹帮妈妈调查了附近五家花卉店近期该种盆栽花卉的售价与日销售量情况,并记录如下:
售价(元/盒) 18 20 22 26 30
日销售量(盒) 54 50 46 38 30
(1)分析表格中数据的变化规律,求日销售量与售价之间的关系式;
(2)根据以上信息,售价定为多少时,小莹妈妈在销售该种花卉中每天能够获得最大利润?
3.某超市以每件元的价格购进一种文具,经过市场调查发现,该文具的每天销售数量(件)与销售单价(元)之间满足一次函数关系,部分数据如表所示:
销售单价元
每天销售数量件
(1)求与之间的函数关系式;
(2)若该超市每天销售这种文具获利元,则销售单价为多少元?
(3)设销售这种文具每天获利(元),当销售单价为多少元时,每天获利最大?最大利润是多少元?
4.龙泉驿水蜜桃有果大质优、色泽艳丽、汁多味甜三大特点,素有“天下第一桃”的美誉.某商家在龙泉驿以元的价格收购了一批水蜜桃后出售,售价不低于元,不超过元.该商家对销售情况进行统计后发现,日销售量与售价(元)之间的函数关系如图所示.
(1)求与之间的函数关系式;
(2)设日销售利润为元,当销售价格定为多少时,日销售利润最大?最大是多少?
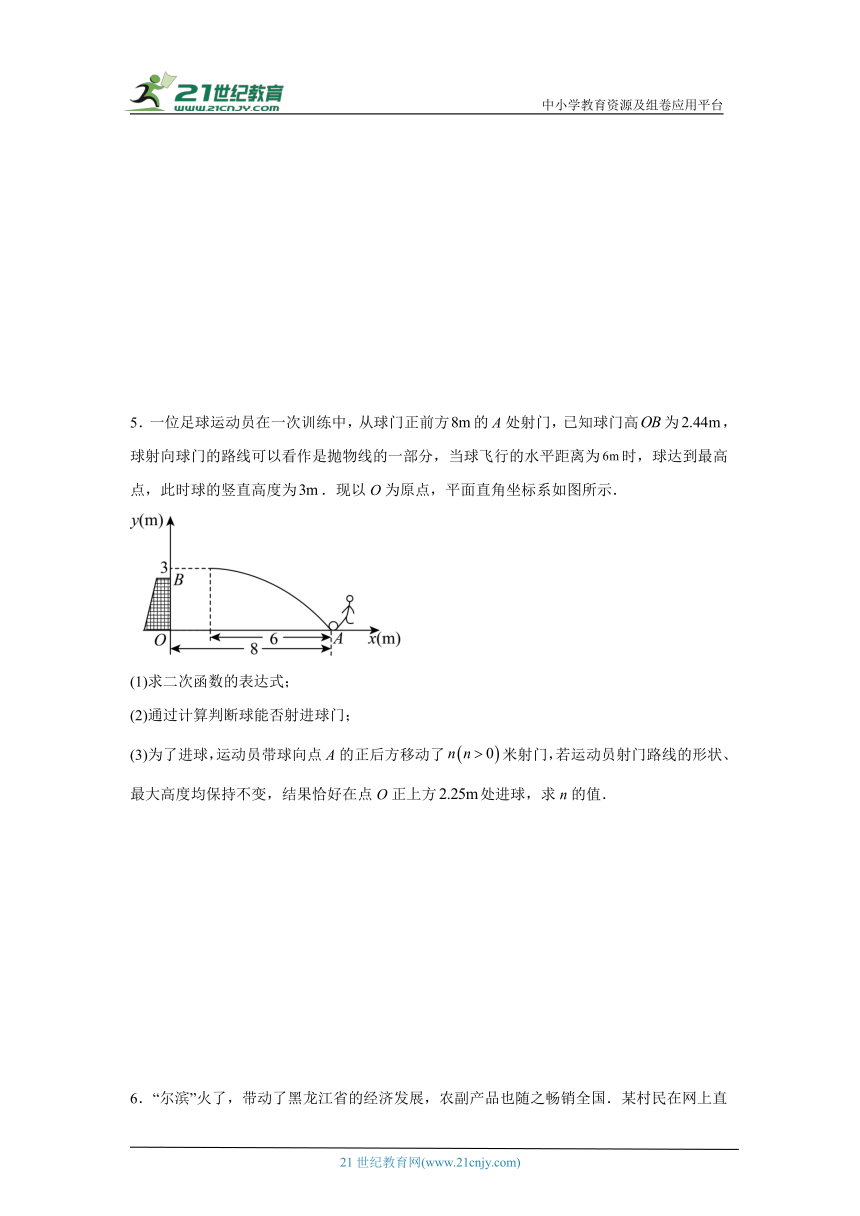
5.一位足球运动员在一次训练中,从球门正前方的A处射门,已知球门高为,球射向球门的路线可以看作是抛物线的一部分,当球飞行的水平距离为时,球达到最高点,此时球的竖直高度为.现以O为原点,平面直角坐标系如图所示.
(1)求二次函数的表达式;
(2)通过计算判断球能否射进球门;
(3)为了进球,运动员带球向点A的正后方移动了米射门,若运动员射门路线的形状、最大高度均保持不变,结果恰好在点O正上方处进球,求n的值.
6.“尔滨”火了,带动了黑龙江省的经济发展,农副产品也随之畅销全国.某村民在网上直播推销某种农副产品,在试销售的天中,第天且为整数)的售价为(元千克).当时,;当时,.销量(千克)与的函数关系式为,已知该产品第天的售价为元千克,第天的售价为元千克,设第天的销售额为(元).
(1) ,_____;
(2)写出第天的销售额与之间的函数关系式;
(3)求在试销售的天中,共有多少天销售额超过元?
7.学校要建一个矩形花圃,其中一边靠墙,另外三边用篱笆围成.已知墙长42m,篱笆长.设垂直于墙的边长为米,平行于墙的边为米,围成的矩形面积为.
(1)求与与的关系式.
(2)围成的矩形花圃面积能否为,若能,求出的值.
(3)围成的矩形花圃面积是否存在最大值?若存在,求出这个最大值,并求出此时的值.
8.麻花是我国的一种特色油炸面食小吃,其色、香、味俱全,品种多样,十分畅销.阳光超市购进了一批麻花礼盒进行销售,成本价为30元/件,根据市场预测,在一段时间内,销售单价为40元/件时,每天的销售量为300件,销售单价每提高10元/件,将少售出50件.
(1)求超市销售该麻花礼盒每天的销售量y(件)与销售单价x(元/件)之间的函数关系式,并求出自变量取值范围;
(2)当销售单价定为多少时,超市销售该麻花礼盒每天获得的利润最大?并求出最大利润.
9.为鼓励大学毕业生自主创业,某市政府出台了相关政策;由政府协调,本而企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.小柳按照政策投资销售本市生产的一种网红螺蛳粉.已知这种网红螺蛳粉的成本价为每箱80元,出厂价为每箱100元,每月销售量(箱)与销售单价(元)之间满足函数关系:.
(1)小柳在开始销售的第1月将螺蛳粉的销售单价定为120元,这个月他销售该螺蛳粉可获利________元.
(2)设小柳销售螺蛳粉获得的月利润为(元),当销售单价为多少元时,月利润最大,最大利润是多少元?
(3)物价部门规定,这种网红螺蛳粉的销售单价不得高于150元,那么政府每个月为他承担的总差价最少为多少元?
10.如图,有长为的篱笆,一面利用墙(墙的最大可用长度为),围成中间隔有一道篱笆(平行于)的矩形花圃.设花圃的一边为,面积为.
(1)若要围成面积为的花圃,则的长是多少?
(2)求为何值时,使花圃面积最大,并求出花圃的最大面积.
11.某旅游景区新进一批文创产品,每件进价是30元,并规定每件售价不得少于50元.根据以往销售经验发现,当每件售价定为50元时,日销售量为500件,每件售价每提高元,日销售量减少5件.设每件售价为x元,日销售量为y件.
(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,日销售利润W(元)最大?最大利润是多少?
(3)当日销售利润不低于6000元时,求每件文创产品售价x的取值范围.
12.小区一水果店购进一种新型蟠桃,蟠桃进价为每千克40元.水果店老板发现:销售量y(千克)与销售单价x(元/千克)之间的关系可近似地看作一次函数,且当时,;当时,,且.
(1)求y关于x的函数解析式:
(2)如果想要每月获得2400元的利润,那么销售单价应定为每千克多少元.
(3)当蟠桃售价每千克多少元时,利润最大,最大利润是多少元.
13.“直播带货”已经成为信息社会中商家的一种新型促销手段,2024年是中国农历甲辰龙年,某主播用3000元购进了一批“小金龙”布偶玩具在直播间销售,由于销售火爆,又用9900元购进了第二批这种玩具,所购数量是第一批购进数量的3倍,但每件的进价贵了3元.
(1)求商场购进第一批“小金龙”每件的进价;
(2)直播间在第二批“小金龙”布偶销售过程中发现,“小金龙”布偶每分钟的销量(件)与销售单价(元)满足一次函数关系,设每分钟的销售利润为元,求与之间的函数关系式,并求最大值.
14.对于向上抛的物体,如果空气阻力忽略不计,有下面的关系式:(h是物体离起点的高度,是初速度,g是重力系数,取,t是抛出后经过的时间).杂技演员抛球表演时,以的初速度把球向上抛出.
(1)1.2秒时球离起点的高度是多少?
(2)几秒后球离起点的高度达到?
15.为了解新建道路的通行能力,查阅资料获知:在某种情况下,车流速度V(单位:千米/时)是车流密度x(单位:辆/千米)的函数,其函数图象如图所示.
(1)当时,求V关于x的函数表达式.
(2)车流量是单位时间内通过观测点的车辆数,计算公式为:车流量车流速度车流密度.若车流速度V不超过80千米/时,求当车流密度x为多少时,车流量P(单位:辆/时)达到最大,并求出这一最大值.
16.网络直播销售已经成为一种热门的销售方式,某生产商在一销售平台上进行直播销售板栗.已知板栗的成本价为6元/ ,每日销售量y()与销售单价x(元/ )满足一次函数关系,下表记录的是有关数据,经销售发现,销售单价不低于成本价且不高于元/ .设公司销售板栗的日获利为w(元).
x(元/ ) 7 8 9
y()
(1)直接写出日销售量y与销售单价x之间的函数关系式为______;(不用写自变量的取值范围)
(2)当销售单价定为多少时,销售这种板栗日获利w最大?最大利润为多少元?
(3)当销售单价在什么范围内时,日获利w不低于元?
17.为了振兴乡村经济,增加村民收入,某村委会干部带领村民在网上直播推销农产品,在试销售的30天中,第x天(且x为整数)的售价p(元/千克)与x的函数关系式(且x为整数),销量q(千克)与x的函数关系式为,已知第5天售价为50元/千克,第10天售价为40元/千克,设第x天的销售额为W元.
(1)______,______;
(2)求销售额W元与x之间的函数关系式,并求第x天时,销售额W最大;
(3)在试销售的30天中,销售额超过1000元的共有______天.
18.学校购买一批钢笔和笔记本奖励给名获奖学生,获得一等奖的学生奖励支钢笔,获得二等奖的学生奖励本笔记本,设获得一等奖的人数为(人).已知购买支钢笔和本笔记本共元,购买支钢笔和本笔记本共元.
(1)钢笔和笔记本的单价分别为多少元?
(2)购买钢笔超过支时,每增加支,单价降低元,若购买奖品的金额为元,求获一等奖的学生人数;
(3)当获一等奖人数为多少时,购买奖品的金额最少?并求出最少金额.
19.某公司以10元/件的价格收购一批产品进行加工销售,销售量y(单位:件)与销售价格(单位:元/件)关系为.设这批产品销售的总利润为w元.
(1)直接写出w与x的函数关系式(不写自变量的取值范围);
(2)求销售利润为3000元时的销售量;
(3)由于市场需要,销售量不能低于360件,当销售价格为多少元时,这批产品获得的利润最大 最大利润是多少元
20.某宾馆有20个房间供游客居住,当每个房间每天的定价为100元时,房间恰好全部住满;当每个房间每天的定价每增加10元时,就会有一个房间空闲.如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用,设每间房间定价x元.
(1)每天有游客居住的房间数为 (用含有x的最简结果表示).
(2)当每间房价定为多少元,宾馆的利润w(元)最大?
(3)宾馆某天统计结果显示,该天利润为1870元,请求出这天每间房的定价x(元)的值.
21.“绿品出塞,北京有约”2023年京蒙消费推介会在北京举行,来自鄂尔多斯的百余种名优特农畜产品集中亮相,阿尔巴斯羊肉独具特色某肉联食品厂销售该产品的成本价格为30元/,若按46元/销售,一个月可以售出4000,销售价每涨1元,月销量就会减少100.
(1)当销售单价定为55元时,计算月销售量和销售利润;
(2)写出月销售利润y与销售价之间的函数解析式;
(3)在(2)的情况下当销售单价定为多少元时会获得最大利润?并求出最大利润.
22.某工厂生产A,B两种型号的环保产品,A产品每件利润200元,B产品每件利润500元,该工厂按计划每天生产两种产品共50件,其中A产品的总利润比B产品少4000元.
(1)求该厂每天生产A产品和B产品各多少件;
(2)据市场调查,B产品的需求量较大,该厂决定在日总产量不变的前提下增加B产品的生产,但B产品相比原计划每多生产一件,每件利润便降低10元.设该厂实际生产B产品的数量比原计划多x件,每天生产A,B产品获得的总利润为w.
①当x为何值时,每天生产A,B产品获得的总利润恰好为16240元?
②若实际生产B产品的数量不少于A产品数量的1.2倍,求总利润w的最大值.
23.某工厂在A,B两城分别生产同种产品共200件,其中A城生产x件,A城生产产品的总成本y(元)与产品数量x(件)之间满足函数关系式,B城生产产品的成本为每件60元.
(1)若A城生产产品的件数为30件,求A,B两城完成这种产品生产任务的总成本.
(2)设A,B两城生产这批产品总成本共w元,求w关于x的函数关系式,并求生产这批产品总成本最小的生产方案;
(3)在(2)的生产方案下,要把这批产品全部运往C,D两地,从A城运往C,D两地的费用分别为10元/件和20元/件;从B城运往C,D两地的费用分别为a元/件(a为常数,)和30元/件;C地需要150件,D地需要50件,请你帮工厂设计出运费最节省的运输方案.
24.某企业设计了一款旅游纪念工艺品,每件的成本是60元,为了合理定价,投放市场进行试销,据市场调查,当销售单价是100元/件时,每天的销售量是80件,若销售单价每降低1元,每天就可多售出4件,但要求销售单价不得低于成本.
(1)写出每天的销售利润y(元)与销售单价x(元/件)之间的函数关系式.
(2)求出当销售单价定为多少元/件时,每天的销售利润最大,最大利润是多少?
25.利民超市购进一种新上市的商品,进价为元/件,超市先进行了天的试销售.销售结束后,对试销情况进行了统计分析,得知日销售量(件)与销售时间(天)之间有如下关系:(,且x为整数);销售价格(元/件)与销售时间(天)之间有如下关系:(,且x为整数).设销售该商品的日利润为(元).
(1)求出(元)与(天)之间的函数关系式;
(2)在这天的试销售中,哪一天的日销售利润最大,哪一天的日销售利润最小?并分别求出这个最大利润和最小利润.
(3)在这天中,日利润不低于元的共有几天?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.(1)每千克应涨价元;
(2).
【分析】()根据题意设每千克应涨价元(),根据总盈余每千克盈余数量列方程,即可求解;
()由题意设每千克涨价元,扣除捐赠后每天销售该种水果获得的利润为元,进而根据结合函数开口向下,对称轴在的右侧即可得出的取值范围;
本题考查一元二次方程和二次函数的应用,根据题意找到题目中的等量关系并列出方程求解是解题的关键.
【详解】(1)解:设每千克应涨价元,
由题意得:,
解得:,,
∵,
∴,
答:每千克应涨价元;
(2)解:设每千克涨价元,扣除捐赠后每天销售该种水果获得的利润为元,则每千克盈利元,每天可售出千克,
依题意得:,
∵当时,随的增大而增大,且,
∴,
解得:,
∴的取值范围为:.
2.(1)
(2)售价定为30元时,每天能够获得最大利润450元
【分析】本题考查一次函数,二次函数的应用,解题的关键是读懂题意,列出函数关系式.
(1)先判断日销售量与售价之间成一次函数,然后用用待定系数法求解即可;
(2)设每天获得的利润为w元,列出二次函数解析式,再由二次函数性质可得答案.
【详解】(1)解:观察表格可知销售量是售价的一次函数;设,
把,代入得:,
解得:,
∴;
(2)解:设每天获得的利润为w元,
由题意得,
,
∴当时,w取最大值450,
∴售价定为30元时,每天能够获得最大利润.
3.(1);
(2)销售单价应为元或元;
(3)当销售单价为元时,每天获利最大,最大利润是元.
【分析】本题考查二次函数的应用,关键是根据利润单件利润销售量列出函数解析式.
(1)设与之间的函数关系式为,然后用待定系数法求函数解析式;
(2)依据利润单件利润销售量列出方程,解答即可;
(3)根据利润单件利润销售量列出函数解析式,然后由函数的性质以及自变量的取值范围求出函数最值.
【详解】(1)设与之间的函数关系式为,
由所给函数图象可知:,
解得:,
故与的函数关系式为;
(2)根据题意得:
,
解得:,,
答:销售单价应为元或元;
(3)由题意可知:
,
,
抛物线开口向下,
对称轴为直线,
当时,有最大值,.
答:当销售单价为元时,每天获利最大,最大利润是元.
4.(1);
(2)当销售价格定为元时,日销售利润最大,最大是元.
【分析】()根据图象,利用待定系数法即可求解;
()根据“日销售利润每千克的利润日销售量”列出与的函数关系式,根据二次函数的性质和的取值范围即可求解;
本题考查了一次函数的应用,二次函数的应用,根据题意列出函数关系式,利用二次函数的性质求解是解题的关键.
【详解】(1)设与之间的函数关系式为,
由所给函数图象可知,图象经过点,,
∴,
解得,
∴与之间的函数关系式为;
(2)∵,
∴
,
∵,
∴当时,的值随值的增大而增大,
∴当时,取得最大值,最大值为,
∴当销售价格定为元时,日销售利润最大,最大是元.
5.(1)
(2)不能,理由见解析
(3)
【分析】本题考查了二次函数的应用,解题的关键是读懂题意,把实际问题转化为数学问题解决.
(1)求出抛物线的顶点坐标,设出抛物线的顶点式,用待定系数法即可求出抛物线表示的二次函数解析式;
(2)当时,求出y的值,再与比较,即可知球能不能射进球门;
(3)移动后的抛物线为,把点代入上式求出n即可;
【详解】(1)解:,
抛物线的顶点坐标为,
设抛物线表示的二次函数的表达式为,
把点代入,得,
解得,
抛物线表示的二次函数的表达式为;
(2)解:当时,,
球不能射进球门;
(3)解:由题意,移动后的抛物线为,
把点代入,得,
解得(舍去),,
的值为.
6.(1),
(2)
(3)在试销售的天中,共有天销售额超过元
【分析】本题考查了一次函数与二次函数的综合应用;
(1)待定系数法求解析式,即可求解;
(2)根据销售额等于销量乘以售价,分段列出函数关系式,即可求解;
(3)根据题意,根据,列出方程,解方程,即可求解.
【详解】(1)解:依题意,将,代入,
∴
解得:
∴
故答案为:,.
(2)解:依题意,
当时,
当时,
∴
(3)解:依题意,当时,
当时,
解得:
为正整数,
∴第天至第天,销售额超过元
(天)
答:在试销售的天中,共有天销售额超过元
7.(1);
(2)能,
(3)的最大值为800,此时
【分析】本题主要考查一元二次方程的应用和二次函数的实际应用:
(1)根据可求出与之间的关系,根据墙的长度可确定的范围;根据面积公式可确立二次函数关系式;
(2)令,得一元二次方程,判断此方程有解,再解方程即可 ;
(3)根据自变量的取值范围和二次函数的性质确定函数的最大值即可.
【详解】(1)解:∵篱笆长,
∴,
∵
∴
∴
∵墙长42m,
∴,
解得,,
∴;
又矩形面积
;
(2)解:令,则,
整理得:,
此时,,
所以,一元二次方程有两个不相等的实数根,
∴围成的矩形花圃面积能为;
∴
∴
∵,
∴;
(3)解:
∵
∴有最大值,
又,
∴当时,取得最大值,此时,
即当时,的最大值为800
8.(1)
(2)当销售单价定为65元时,超市销售该麻花礼盒每天获得的利润最大,最大利润为6125元;
【分析】本题考查了一次函数的应用,二次函数的应用,准确理解题意,熟练掌握知识点是解题的关键.
(1)根据每天的销售量为300件,销售单价每提高10元/件,将少售出50件求解即可;
(2)设利润为w,求出关于w的二次函数,根据二次函数的性质求解即可;
【详解】(1)解:由题意可得:
;
(2)设利润为w元,由题意得
,
∴当时,w最大为6125,
∴当销售单价定为65元时,超市销售该麻花礼盒每天获得的利润最大,最大利润为6125元;
9.(1)6400
(2)140元;最大利润7200元
(3)最少2000元
【分析】本题主要考查了一次函数与二次函数的综合应用,解题的关键是理清“成本价”、“出厂价”、“销售价”、“利润”之间的关系.
(1)先算出销售量,然后再算出获利多少元.注意:利润=销售量(销售价-成本价)
(2)根据题意列出月利润的二次函数关系式,整理成顶点式,可求得最大值.
(3)从销售单价的限额范围入手,表示出销售量的范围,最后再表示出政府承担的总差价即可得到结论.
【详解】(1)解:销售单价时,销售量,
共获利:(元),
故答案为:.
(2)设销售单价为x元时,月利润最大,
根据题意得: ,
当时,w值最大,最大值为7200,
答:销售单价为140元时,月利润最大,最大利润是7200元.
(3)依据题意知,销售单价,则销售量,
∴政府每个月为他承担的总差价:
答:那么政府每个月为他承担的总差价最少为2000元.
10.(1)AB的长为
(2)AB为时,花圃面积最大,花圃的最大面积为
【分析】本题考查了二次函数和一元二次方程的应用,根据题目的条件,合理地建立函数关系式,会判别函数关系式的类别,从而利用这种函数的性质解题.
(1)根据题意列出一元二次方程求解即可;
(2)根据题意得到,根据函数的性质以及自变量的取值范围求函数最值.
【详解】(1)解:根据题意得,,
解得,,
当时,,符合题意;
当时,,不符合题意,舍去,
∴当的长为时,花圃的面积为;
(2)解:花圃的面积,
而由题意:,
即,
∵,
∴当时,y随x的增大而减小,
∴当时面积最大,最大面积为.
11.(1)
(2)每件产品售价定为65元时,日销售利润最大,最大利润是12250元.
(3)
【分析】本题考查了二次函数的实际应用,解题的关键是正确理解题意,根据题意列出函数表达式,熟练掌握二次函数的性质.
(1)根据“每件售价定为50元时,日销售量为500件,每件售价每提高元,日销售量减少5件”即可列出函数关系式;
(2)根据总利润=单件利润×数量,列出W关于x的函数关系式,再根据题意列出不等式组,求出x的取值范围,再结合二次函数的性质,即可解答;
(3)先求出时x的值,再结合二次函数的性质,以及(2)中得出x的取值范围,即可解答.
【详解】(1)解:由题意得:,
∴y与x之间的函数关系式为;
(2)解:由题意得
,
由题意得,
解得,
∵,
∴当时,W取得最大值,最大值为12250,
答:当每件产品售价定为65元时,日销售利润W(元)最大,最大利润是12250元;
(3)解:当元时,,
解得,
∵,
∴图象开口向下,
∴当时,,
又∵,
∴,
答:当日销售利润不低于6000元时,每件文创产品售价x的取值范围为.
12.(1)
(2)销售单价应定为每千克60元或70元
(3)当蟠桃售价每千克65元时,利润最大,最大利润是2500元
【分析】本题考查一次函数解析式,一元二次方程的实际应用,二次函数的实际应用.
(1)设y关于x的函数解析式为,根据当时,;当时,,利用待定系数法求解即可;
(2)根据利润销售量(售价进价)建立方程求解即可;
(3)设利润为,根据利润销售量(售价进价)建立函数关系式,利用二次函数的性质即可解答.
【详解】(1)解:设y关于x的函数解析式为,
根据题意得:,
解得:,
y关于x的函数解析式为;
(2)解:根据题意得:,即,
解得:,
答:销售单价应定为每千克60元或70元;
(3)解:设利润为,根据题意得:
,即,
,
,
当时,有最大值,最大值为,
答:当蟠桃售价每千克65元时,利润最大,最大利润是2500元.
13.(1)30元
(2);最大值160元
【分析】本题考查了分式方程的应用、二次函数的应用,正确列出分式方程,熟练掌握二次函数的性质是解此题的关键.
(1)设购进第一批“小金龙”每件进价为元,则购进第二批“小金龙”每件进价为元,根据“第二批所购数量是第一批购进数量的3倍”列出分式方程,解方程即可得出答案;
(2)由题意得得出与之间的函数关系式,利用二次函数的性质求解即可.
【详解】(1)解:设购进第一批“小金龙”每件进价为元,则购进第二批“小金龙”每件进价为元,
由题意得:,
解得:,
经检验,是原分式方程的根,且符合题意,
商场购进第一批“小金龙”每件的进价为30元.
(2)解:由题意得:,
当时,有最大值160元,
答:最大值为160元.
14.(1)秒时球离起点的高度是;
(2)秒或秒后球离起点的高度达到.
【分析】本题为二次函数实际应用问题,解答时注意将相应的函数值或自变量值代入函数关系式中求解即可.
(1)把代入即可求解;
(2)把代入求t即可.
【详解】(1)解:由题意,将分别代入函数关系式,
得,
当时,代入解得,
∴秒时球离起点的高度是;
(2)解:当时,,
解得.
故秒或秒后球离起点的高度达到.
15.(1)
(2)时,P的最大值为4418
【分析】此题主要考查了一次函数的应用以及二次函数的应用以及函数最值求法,得出关于的函数关系式是解题关键.
(1)直接利用待定系数法求一次函数解析式进而得出答案;
(2)根据计算公式为:车流量车流速度车流密度可得,再利用配方法求出最值即可.
【详解】(1)解:当时,.
当时,设,
由图象可知,,
解得:,
当时,;
(2)根据题意,得.
答:当车流密度为94辆千米时,车流量最大,为4418辆时.
16.(1)
(2)当销售单价定为元时,日获利w最大,最大利润为元
(3)
【分析】(1)设日销售量y与销售单价x之间的函数关系式,将,,代入得,,计算求解,进而可得结果;
(2)依题意得,,由,,可知当时,日获利w最大,最大利润为元;
(3)令,则,可求或,由,可得,由,可得.
【详解】(1)解:设日销售量y与销售单价x之间的函数关系式,
将,,代入得,,
解得,,
∴日销售量y与销售单价x之间的函数关系式;
(2)解:依题意得,,
∵,,
∴当时,日获利w最大,最大利润为元;
(3)解:令,则,
解得,或,
∵,
∴,
又∵,
∴.
【点睛】本题考查了一次函数的应用,二次函数的应用,二次函数的图象与性质,二次函数与一元二次方程的关系等知识.熟练掌握一次函数的应用,二次函数的应用,二次函数的图象与性质,二次函数与一元二次方程的关系是解题的关键.
17.(1);60
(2);第30天时,销售额W最大
(3)7
【分析】本题考查一次函数和二次函数的应用,解题的关键是读懂题意,列出函数关系式.
(1)用待定系数法可得,的值;
(2)由销售额,分两种情况可得函数关系式,再分别 根据函数值比较即可得答案;
(3)分两种情况,结合(2)可列出方程解得答案.
【详解】(1)解:把,代入得:
,
解得,
故答案为:,60;
(2)解:由(1)可得,
当时,;
当时,;
;
当,,
∵,
∴当时,W有最大值,最大值为800;
当时,,
∵,
∴W随x增大而增大,
∴时,W有最大值,最大值为,
∵,
∴第30天时,销售额W最大.
(3)解:在中,令得:,
整理得,
方程无实数解;
由得,
整数,
可取24,25,26,27,28,29,30,
销售额超过1000元的共有7天.
18.(1)钢笔的单价为元,笔记本的单价为元
(2)人
(3)一等奖人时,购买奖品的金额最少,最少金额为元
【分析】本题考查了二元一次方程组的应用、一元二次方程的应用以及二次函数的应用,
(1)设钢笔的单价为元,笔记本的单价为元,根据“购买支钢笔和本笔记本共元,购买支钢笔和本笔记本共元”,即可得出关于、的二元一次方程组,解之即可得出结论;
(2)设获得一等奖的人数为人,则获得二等奖的人数为人,钢笔的单价为元,根据购买奖品的金额为元,即可得出关于的一元二次方程,解之取其符合题意的值即可得出结论;
(3)设购买奖品的总金额为元,利用总价单价数量,即可得出关于的函数关系式,再利用二次函数的性质,即可解决最值问题;
解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)找准等量关系,正确列出一元二次方程;(3)根据各数量之间的关系,找出关于的函数关系式.
【详解】(1)解:设钢笔的单价为元,笔记本的单价为元,
依题意,得:,
解得:,
答:钢笔的单价为元,笔记本的单价为元;
(2)设获得一等奖人数为人,则获得二等奖人数为个,则钢笔的单价为元,
依题意,得:,
解得:,(舍去),
∴获得一等奖学生人数为人;
(3)设购买奖品的总金额为元,则,
即,
∵,
∴抛物线的开口向下,对称轴为,
∵,为整数,
∴当,随的增加而减小,
∴当,有最小值为元,
∴一等奖人时,购买奖品的金额最少,最少金额为元.
19.(1)
(2)销售利润为3000元时的销售量为300件
(3)当销售价格为18元时,这批产品获得的利润最大,最大利润是2880元
【分析】本题考查二次函数的应用、一元一次不等式的应用,解答的关键是读懂题意,列出函数关系式,运算二次函数性质解决问题.
(1)根据总利润等于单件利润乘以销售量列函数关系式即可;
(2)求出当时的x值即可;
(3)先配方,利用求二次函数的最值的方法求解即可.
【详解】(1)解:根据题意,,
即w与x的函数关系式为;
(2)解:当时,由得,
解得,
∴,
答:销售利润为3000元时的销售量为300件;
(3)解:,
∵销售量不能低于360件,
∴且,
∴,又,
∴当时,w最大,最大值为2880,
答:当销售价格为18元时,这批产品获得的利润最大,最大利润是2880元.
20.(1)
(2)当每间房价定为160元,宾馆的利润w最大为1960元
(3)这天每间房的定价是130元或190元
【分析】本题考查二次函数及一元二次方程的应用,解题的关键是读懂题意,列出函数关系式.
(1)根据当每个房间每天的定价每增加10元时,就会有一个房间空闲知:每间房间定价元时,每天有游客居住的房间数为;
(2)根据总利润每个房间利润房间数量可得,由二次函数性质可得答案;
(3)由该天利润为1870元,结合(2)可得,即可解得答案.
【详解】(1)解:根据题意知,每间房间定价元时,每天有游客居住的房间数为;
故答案为:;
(2)解:根据题意得:,
,
当时,取最大值,最大值为1960元;
答:当每间房价定为160元,宾馆的利润最大为1960元;
(3)解:该天利润为1870元,
,
解得或,
答:这天每间房的定价是130元或190元.
21.(1)销量为千克,利润为元;
(2)
(3)当时,有最大利润为元.
【分析】本题考查的是二次函数的实际应用,理解题意,确定正确的函数关系式是解本题的关键;
(1)根据“销售单价每涨1元,月销售量就减少100千克”,可知:月销售量(销售单价,再计算利润即可;
(2)根据总利润等于每千克的利润乘以销售量可得函数关系式;
(3)利用二次函数的性质可得二次函数的最值.
【详解】(1)解:∵按46元/销售,一个月可以售出4000,销售价每涨1元,月销量就会减少100.
∴销售单价定为55元时,每千克的利润为(元),
销售数量为:(千克),
∴销售利润为(元);
(2)由题意可得:月销售利润y与销售价之间的函数解析式为:
;
(3)∵
∵,
∴当时,有最大利润为元.
22.(1)每天生产A产品30件,B产品20件
(2)①或6;②
【分析】本题主要考查了二次函数的实际应用:
(1)设每天生产A产品x件,则每天生产B产品件,由题意列出方程可得答案;
(2)根据题意列出函数解析式,由二次函数的性质求最值.
【详解】(1)解:设每天生产A产品x件,则每天生产B产品件,
由题意得:,
解得:,
每天生产B产品为件;
答:每天生产A产品30件,B产品20件
(2)解:①由题意得:
令,则,
解得或6
②由题意得:
实际生产B产品的数量不少于A产品数量的1.2倍,
,
解得:
,且
当时,w随x的增大而减小,
取正整数,
当时,w有最大值,即.
23.(1)11700元
(2),城生产20件,城生产180件
(3)当时,从A城运往C地件,从B城运往C地130件,运往地50件,运费最小;时,从A城运往D地件,从B城运往C地150件,运往地30件,运费最小
【分析】本题考查二次函数的实际应用,一次函数的实际应用,找准等量关系,正确的列出函数关系式,是解题的关键.
(1)分别求出两城各自的总成本,相加即可;
(2)根据总成本等于两城各自的总成本之和,列出函数关系式,利用二次函数的性质,求出最值即可;
(3)设从A城运往C地件,总运费为元,列出一次函数,利用一次函数的性质进行求解即可.
【详解】(1)解:当A城生产产品的件数为30件时,则:B城生产产品的件数为件,
∵,
∴当时,,
∴A,B两城完成这种产品生产任务的总成本为元;
(2)由题意,得:,
∴,
∴当,即:城生产20件,城生产件时,总成本最低;
∴城生产20件,城生产180件;
(3)设从A城运往C地件,总运费为元,则从城运往地件,从B城运往C地件,运往地件,由题意,得:
,
∵且,
∴,
当,即时,随的增大而减下,
∴当时,最小为:;
此时从A城运往C地件,从B城运往C地130件,运往地50件,运费最小;
当,即时,随的增大而增大,
∴当时,最小为,
此时从A城运往D地件,从B城运往C地150件,运往地30件,运费最小.
24.(1)
(2)当销售单价定为90元/件时,每天的销售利润最大,最大利润是3600元
【分析】(1)根据销售单价为x元,则降价元,每件的盈利元,每天可售出件,根据题意,得,解得即可.
(2)根据,构造二次函数,根据抛物线的最值,解之即可得出x的值即可求得.
本题考查了一元二次方程的应用,二次函数的最值,最大利润问题,熟练掌握一元二次方程的应用,二次函数的最值是解题的关键.
【详解】(1)根据销售单价为x元,则降价元,
每件的盈利元,每天可售出件,
根据题意,得,
故.
(2)由(1)可得.
∵,,
∴当时,y取得最大值,最大值为3600.
答:当销售单价定为90元/件时,每天的销售利润最大,最大利润是3600元.
25.(1)(,且为整数)
(2)第天日销售利润最大,最大利润为元;第天日销售利润最小,最小利润为元
(3)利润不低于元的共有天
【分析】本题考查了二次函数的实际应用,熟练掌握二次函数的图象和性质是解题的关键.
(1)根据销售问题中的基本等量关系:销售利润=日销售量×(一件的销售价-一件的进价),建立函数关系式即可.
(2)将(1)中函数关系式配方,可得其顶点式,结合自变量的范围,根据二次函数的性质可得函数的最值情况.
(3)令,即,解得,因为,且x为整数,所以利润不低于元的共有天.
【详解】(1)解:根据题意,得
(,且为整数).
(2)∵,
∴当时,取最大值为元;
当时,取最小值为元.
故:第天日销售利润最大,最大利润为元;第天日销售利润最小,最小利润为元.
(3)令,即,
解得,
∵,且x为整数,
∴利润不低于元的共有天.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
人教版九年级上册数学第二十二章 二次函数应用题专题训练
1.某水果超市经销一种水果,售价每千克元.每千克盈利元,每天可售出千克,调查发现,进货价不变的情况下,每千克涨价元,日销售量将减少千克.规定每千克涨价不能超过元.
(1)该超市希望每天盈利元,那么每千克应涨价多少元?
(2)超市决定每卖出千克捐赠元()给贫困山区学生,若每天盈利随着售价的增加而增大,求的取值范围.
2.小莹妈妈的花卉超市以15元/盆的价格新购进了某种盆栽花卉,为了确定售价,小莹帮妈妈调查了附近五家花卉店近期该种盆栽花卉的售价与日销售量情况,并记录如下:
售价(元/盒) 18 20 22 26 30
日销售量(盒) 54 50 46 38 30
(1)分析表格中数据的变化规律,求日销售量与售价之间的关系式;
(2)根据以上信息,售价定为多少时,小莹妈妈在销售该种花卉中每天能够获得最大利润?
3.某超市以每件元的价格购进一种文具,经过市场调查发现,该文具的每天销售数量(件)与销售单价(元)之间满足一次函数关系,部分数据如表所示:
销售单价元
每天销售数量件
(1)求与之间的函数关系式;
(2)若该超市每天销售这种文具获利元,则销售单价为多少元?
(3)设销售这种文具每天获利(元),当销售单价为多少元时,每天获利最大?最大利润是多少元?
4.龙泉驿水蜜桃有果大质优、色泽艳丽、汁多味甜三大特点,素有“天下第一桃”的美誉.某商家在龙泉驿以元的价格收购了一批水蜜桃后出售,售价不低于元,不超过元.该商家对销售情况进行统计后发现,日销售量与售价(元)之间的函数关系如图所示.
(1)求与之间的函数关系式;
(2)设日销售利润为元,当销售价格定为多少时,日销售利润最大?最大是多少?
5.一位足球运动员在一次训练中,从球门正前方的A处射门,已知球门高为,球射向球门的路线可以看作是抛物线的一部分,当球飞行的水平距离为时,球达到最高点,此时球的竖直高度为.现以O为原点,平面直角坐标系如图所示.
(1)求二次函数的表达式;
(2)通过计算判断球能否射进球门;
(3)为了进球,运动员带球向点A的正后方移动了米射门,若运动员射门路线的形状、最大高度均保持不变,结果恰好在点O正上方处进球,求n的值.
6.“尔滨”火了,带动了黑龙江省的经济发展,农副产品也随之畅销全国.某村民在网上直播推销某种农副产品,在试销售的天中,第天且为整数)的售价为(元千克).当时,;当时,.销量(千克)与的函数关系式为,已知该产品第天的售价为元千克,第天的售价为元千克,设第天的销售额为(元).
(1) ,_____;
(2)写出第天的销售额与之间的函数关系式;
(3)求在试销售的天中,共有多少天销售额超过元?
7.学校要建一个矩形花圃,其中一边靠墙,另外三边用篱笆围成.已知墙长42m,篱笆长.设垂直于墙的边长为米,平行于墙的边为米,围成的矩形面积为.
(1)求与与的关系式.
(2)围成的矩形花圃面积能否为,若能,求出的值.
(3)围成的矩形花圃面积是否存在最大值?若存在,求出这个最大值,并求出此时的值.
8.麻花是我国的一种特色油炸面食小吃,其色、香、味俱全,品种多样,十分畅销.阳光超市购进了一批麻花礼盒进行销售,成本价为30元/件,根据市场预测,在一段时间内,销售单价为40元/件时,每天的销售量为300件,销售单价每提高10元/件,将少售出50件.
(1)求超市销售该麻花礼盒每天的销售量y(件)与销售单价x(元/件)之间的函数关系式,并求出自变量取值范围;
(2)当销售单价定为多少时,超市销售该麻花礼盒每天获得的利润最大?并求出最大利润.
9.为鼓励大学毕业生自主创业,某市政府出台了相关政策;由政府协调,本而企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.小柳按照政策投资销售本市生产的一种网红螺蛳粉.已知这种网红螺蛳粉的成本价为每箱80元,出厂价为每箱100元,每月销售量(箱)与销售单价(元)之间满足函数关系:.
(1)小柳在开始销售的第1月将螺蛳粉的销售单价定为120元,这个月他销售该螺蛳粉可获利________元.
(2)设小柳销售螺蛳粉获得的月利润为(元),当销售单价为多少元时,月利润最大,最大利润是多少元?
(3)物价部门规定,这种网红螺蛳粉的销售单价不得高于150元,那么政府每个月为他承担的总差价最少为多少元?
10.如图,有长为的篱笆,一面利用墙(墙的最大可用长度为),围成中间隔有一道篱笆(平行于)的矩形花圃.设花圃的一边为,面积为.
(1)若要围成面积为的花圃,则的长是多少?
(2)求为何值时,使花圃面积最大,并求出花圃的最大面积.
11.某旅游景区新进一批文创产品,每件进价是30元,并规定每件售价不得少于50元.根据以往销售经验发现,当每件售价定为50元时,日销售量为500件,每件售价每提高元,日销售量减少5件.设每件售价为x元,日销售量为y件.
(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,日销售利润W(元)最大?最大利润是多少?
(3)当日销售利润不低于6000元时,求每件文创产品售价x的取值范围.
12.小区一水果店购进一种新型蟠桃,蟠桃进价为每千克40元.水果店老板发现:销售量y(千克)与销售单价x(元/千克)之间的关系可近似地看作一次函数,且当时,;当时,,且.
(1)求y关于x的函数解析式:
(2)如果想要每月获得2400元的利润,那么销售单价应定为每千克多少元.
(3)当蟠桃售价每千克多少元时,利润最大,最大利润是多少元.
13.“直播带货”已经成为信息社会中商家的一种新型促销手段,2024年是中国农历甲辰龙年,某主播用3000元购进了一批“小金龙”布偶玩具在直播间销售,由于销售火爆,又用9900元购进了第二批这种玩具,所购数量是第一批购进数量的3倍,但每件的进价贵了3元.
(1)求商场购进第一批“小金龙”每件的进价;
(2)直播间在第二批“小金龙”布偶销售过程中发现,“小金龙”布偶每分钟的销量(件)与销售单价(元)满足一次函数关系,设每分钟的销售利润为元,求与之间的函数关系式,并求最大值.
14.对于向上抛的物体,如果空气阻力忽略不计,有下面的关系式:(h是物体离起点的高度,是初速度,g是重力系数,取,t是抛出后经过的时间).杂技演员抛球表演时,以的初速度把球向上抛出.
(1)1.2秒时球离起点的高度是多少?
(2)几秒后球离起点的高度达到?
15.为了解新建道路的通行能力,查阅资料获知:在某种情况下,车流速度V(单位:千米/时)是车流密度x(单位:辆/千米)的函数,其函数图象如图所示.
(1)当时,求V关于x的函数表达式.
(2)车流量是单位时间内通过观测点的车辆数,计算公式为:车流量车流速度车流密度.若车流速度V不超过80千米/时,求当车流密度x为多少时,车流量P(单位:辆/时)达到最大,并求出这一最大值.
16.网络直播销售已经成为一种热门的销售方式,某生产商在一销售平台上进行直播销售板栗.已知板栗的成本价为6元/ ,每日销售量y()与销售单价x(元/ )满足一次函数关系,下表记录的是有关数据,经销售发现,销售单价不低于成本价且不高于元/ .设公司销售板栗的日获利为w(元).
x(元/ ) 7 8 9
y()
(1)直接写出日销售量y与销售单价x之间的函数关系式为______;(不用写自变量的取值范围)
(2)当销售单价定为多少时,销售这种板栗日获利w最大?最大利润为多少元?
(3)当销售单价在什么范围内时,日获利w不低于元?
17.为了振兴乡村经济,增加村民收入,某村委会干部带领村民在网上直播推销农产品,在试销售的30天中,第x天(且x为整数)的售价p(元/千克)与x的函数关系式(且x为整数),销量q(千克)与x的函数关系式为,已知第5天售价为50元/千克,第10天售价为40元/千克,设第x天的销售额为W元.
(1)______,______;
(2)求销售额W元与x之间的函数关系式,并求第x天时,销售额W最大;
(3)在试销售的30天中,销售额超过1000元的共有______天.
18.学校购买一批钢笔和笔记本奖励给名获奖学生,获得一等奖的学生奖励支钢笔,获得二等奖的学生奖励本笔记本,设获得一等奖的人数为(人).已知购买支钢笔和本笔记本共元,购买支钢笔和本笔记本共元.
(1)钢笔和笔记本的单价分别为多少元?
(2)购买钢笔超过支时,每增加支,单价降低元,若购买奖品的金额为元,求获一等奖的学生人数;
(3)当获一等奖人数为多少时,购买奖品的金额最少?并求出最少金额.
19.某公司以10元/件的价格收购一批产品进行加工销售,销售量y(单位:件)与销售价格(单位:元/件)关系为.设这批产品销售的总利润为w元.
(1)直接写出w与x的函数关系式(不写自变量的取值范围);
(2)求销售利润为3000元时的销售量;
(3)由于市场需要,销售量不能低于360件,当销售价格为多少元时,这批产品获得的利润最大 最大利润是多少元
20.某宾馆有20个房间供游客居住,当每个房间每天的定价为100元时,房间恰好全部住满;当每个房间每天的定价每增加10元时,就会有一个房间空闲.如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用,设每间房间定价x元.
(1)每天有游客居住的房间数为 (用含有x的最简结果表示).
(2)当每间房价定为多少元,宾馆的利润w(元)最大?
(3)宾馆某天统计结果显示,该天利润为1870元,请求出这天每间房的定价x(元)的值.
21.“绿品出塞,北京有约”2023年京蒙消费推介会在北京举行,来自鄂尔多斯的百余种名优特农畜产品集中亮相,阿尔巴斯羊肉独具特色某肉联食品厂销售该产品的成本价格为30元/,若按46元/销售,一个月可以售出4000,销售价每涨1元,月销量就会减少100.
(1)当销售单价定为55元时,计算月销售量和销售利润;
(2)写出月销售利润y与销售价之间的函数解析式;
(3)在(2)的情况下当销售单价定为多少元时会获得最大利润?并求出最大利润.
22.某工厂生产A,B两种型号的环保产品,A产品每件利润200元,B产品每件利润500元,该工厂按计划每天生产两种产品共50件,其中A产品的总利润比B产品少4000元.
(1)求该厂每天生产A产品和B产品各多少件;
(2)据市场调查,B产品的需求量较大,该厂决定在日总产量不变的前提下增加B产品的生产,但B产品相比原计划每多生产一件,每件利润便降低10元.设该厂实际生产B产品的数量比原计划多x件,每天生产A,B产品获得的总利润为w.
①当x为何值时,每天生产A,B产品获得的总利润恰好为16240元?
②若实际生产B产品的数量不少于A产品数量的1.2倍,求总利润w的最大值.
23.某工厂在A,B两城分别生产同种产品共200件,其中A城生产x件,A城生产产品的总成本y(元)与产品数量x(件)之间满足函数关系式,B城生产产品的成本为每件60元.
(1)若A城生产产品的件数为30件,求A,B两城完成这种产品生产任务的总成本.
(2)设A,B两城生产这批产品总成本共w元,求w关于x的函数关系式,并求生产这批产品总成本最小的生产方案;
(3)在(2)的生产方案下,要把这批产品全部运往C,D两地,从A城运往C,D两地的费用分别为10元/件和20元/件;从B城运往C,D两地的费用分别为a元/件(a为常数,)和30元/件;C地需要150件,D地需要50件,请你帮工厂设计出运费最节省的运输方案.
24.某企业设计了一款旅游纪念工艺品,每件的成本是60元,为了合理定价,投放市场进行试销,据市场调查,当销售单价是100元/件时,每天的销售量是80件,若销售单价每降低1元,每天就可多售出4件,但要求销售单价不得低于成本.
(1)写出每天的销售利润y(元)与销售单价x(元/件)之间的函数关系式.
(2)求出当销售单价定为多少元/件时,每天的销售利润最大,最大利润是多少?
25.利民超市购进一种新上市的商品,进价为元/件,超市先进行了天的试销售.销售结束后,对试销情况进行了统计分析,得知日销售量(件)与销售时间(天)之间有如下关系:(,且x为整数);销售价格(元/件)与销售时间(天)之间有如下关系:(,且x为整数).设销售该商品的日利润为(元).
(1)求出(元)与(天)之间的函数关系式;
(2)在这天的试销售中,哪一天的日销售利润最大,哪一天的日销售利润最小?并分别求出这个最大利润和最小利润.
(3)在这天中,日利润不低于元的共有几天?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.(1)每千克应涨价元;
(2).
【分析】()根据题意设每千克应涨价元(),根据总盈余每千克盈余数量列方程,即可求解;
()由题意设每千克涨价元,扣除捐赠后每天销售该种水果获得的利润为元,进而根据结合函数开口向下,对称轴在的右侧即可得出的取值范围;
本题考查一元二次方程和二次函数的应用,根据题意找到题目中的等量关系并列出方程求解是解题的关键.
【详解】(1)解:设每千克应涨价元,
由题意得:,
解得:,,
∵,
∴,
答:每千克应涨价元;
(2)解:设每千克涨价元,扣除捐赠后每天销售该种水果获得的利润为元,则每千克盈利元,每天可售出千克,
依题意得:,
∵当时,随的增大而增大,且,
∴,
解得:,
∴的取值范围为:.
2.(1)
(2)售价定为30元时,每天能够获得最大利润450元
【分析】本题考查一次函数,二次函数的应用,解题的关键是读懂题意,列出函数关系式.
(1)先判断日销售量与售价之间成一次函数,然后用用待定系数法求解即可;
(2)设每天获得的利润为w元,列出二次函数解析式,再由二次函数性质可得答案.
【详解】(1)解:观察表格可知销售量是售价的一次函数;设,
把,代入得:,
解得:,
∴;
(2)解:设每天获得的利润为w元,
由题意得,
,
∴当时,w取最大值450,
∴售价定为30元时,每天能够获得最大利润.
3.(1);
(2)销售单价应为元或元;
(3)当销售单价为元时,每天获利最大,最大利润是元.
【分析】本题考查二次函数的应用,关键是根据利润单件利润销售量列出函数解析式.
(1)设与之间的函数关系式为,然后用待定系数法求函数解析式;
(2)依据利润单件利润销售量列出方程,解答即可;
(3)根据利润单件利润销售量列出函数解析式,然后由函数的性质以及自变量的取值范围求出函数最值.
【详解】(1)设与之间的函数关系式为,
由所给函数图象可知:,
解得:,
故与的函数关系式为;
(2)根据题意得:
,
解得:,,
答:销售单价应为元或元;
(3)由题意可知:
,
,
抛物线开口向下,
对称轴为直线,
当时,有最大值,.
答:当销售单价为元时,每天获利最大,最大利润是元.
4.(1);
(2)当销售价格定为元时,日销售利润最大,最大是元.
【分析】()根据图象,利用待定系数法即可求解;
()根据“日销售利润每千克的利润日销售量”列出与的函数关系式,根据二次函数的性质和的取值范围即可求解;
本题考查了一次函数的应用,二次函数的应用,根据题意列出函数关系式,利用二次函数的性质求解是解题的关键.
【详解】(1)设与之间的函数关系式为,
由所给函数图象可知,图象经过点,,
∴,
解得,
∴与之间的函数关系式为;
(2)∵,
∴
,
∵,
∴当时,的值随值的增大而增大,
∴当时,取得最大值,最大值为,
∴当销售价格定为元时,日销售利润最大,最大是元.
5.(1)
(2)不能,理由见解析
(3)
【分析】本题考查了二次函数的应用,解题的关键是读懂题意,把实际问题转化为数学问题解决.
(1)求出抛物线的顶点坐标,设出抛物线的顶点式,用待定系数法即可求出抛物线表示的二次函数解析式;
(2)当时,求出y的值,再与比较,即可知球能不能射进球门;
(3)移动后的抛物线为,把点代入上式求出n即可;
【详解】(1)解:,
抛物线的顶点坐标为,
设抛物线表示的二次函数的表达式为,
把点代入,得,
解得,
抛物线表示的二次函数的表达式为;
(2)解:当时,,
球不能射进球门;
(3)解:由题意,移动后的抛物线为,
把点代入,得,
解得(舍去),,
的值为.
6.(1),
(2)
(3)在试销售的天中,共有天销售额超过元
【分析】本题考查了一次函数与二次函数的综合应用;
(1)待定系数法求解析式,即可求解;
(2)根据销售额等于销量乘以售价,分段列出函数关系式,即可求解;
(3)根据题意,根据,列出方程,解方程,即可求解.
【详解】(1)解:依题意,将,代入,
∴
解得:
∴
故答案为:,.
(2)解:依题意,
当时,
当时,
∴
(3)解:依题意,当时,
当时,
解得:
为正整数,
∴第天至第天,销售额超过元
(天)
答:在试销售的天中,共有天销售额超过元
7.(1);
(2)能,
(3)的最大值为800,此时
【分析】本题主要考查一元二次方程的应用和二次函数的实际应用:
(1)根据可求出与之间的关系,根据墙的长度可确定的范围;根据面积公式可确立二次函数关系式;
(2)令,得一元二次方程,判断此方程有解,再解方程即可 ;
(3)根据自变量的取值范围和二次函数的性质确定函数的最大值即可.
【详解】(1)解:∵篱笆长,
∴,
∵
∴
∴
∵墙长42m,
∴,
解得,,
∴;
又矩形面积
;
(2)解:令,则,
整理得:,
此时,,
所以,一元二次方程有两个不相等的实数根,
∴围成的矩形花圃面积能为;
∴
∴
∵,
∴;
(3)解:
∵
∴有最大值,
又,
∴当时,取得最大值,此时,
即当时,的最大值为800
8.(1)
(2)当销售单价定为65元时,超市销售该麻花礼盒每天获得的利润最大,最大利润为6125元;
【分析】本题考查了一次函数的应用,二次函数的应用,准确理解题意,熟练掌握知识点是解题的关键.
(1)根据每天的销售量为300件,销售单价每提高10元/件,将少售出50件求解即可;
(2)设利润为w,求出关于w的二次函数,根据二次函数的性质求解即可;
【详解】(1)解:由题意可得:
;
(2)设利润为w元,由题意得
,
∴当时,w最大为6125,
∴当销售单价定为65元时,超市销售该麻花礼盒每天获得的利润最大,最大利润为6125元;
9.(1)6400
(2)140元;最大利润7200元
(3)最少2000元
【分析】本题主要考查了一次函数与二次函数的综合应用,解题的关键是理清“成本价”、“出厂价”、“销售价”、“利润”之间的关系.
(1)先算出销售量,然后再算出获利多少元.注意:利润=销售量(销售价-成本价)
(2)根据题意列出月利润的二次函数关系式,整理成顶点式,可求得最大值.
(3)从销售单价的限额范围入手,表示出销售量的范围,最后再表示出政府承担的总差价即可得到结论.
【详解】(1)解:销售单价时,销售量,
共获利:(元),
故答案为:.
(2)设销售单价为x元时,月利润最大,
根据题意得: ,
当时,w值最大,最大值为7200,
答:销售单价为140元时,月利润最大,最大利润是7200元.
(3)依据题意知,销售单价,则销售量,
∴政府每个月为他承担的总差价:
答:那么政府每个月为他承担的总差价最少为2000元.
10.(1)AB的长为
(2)AB为时,花圃面积最大,花圃的最大面积为
【分析】本题考查了二次函数和一元二次方程的应用,根据题目的条件,合理地建立函数关系式,会判别函数关系式的类别,从而利用这种函数的性质解题.
(1)根据题意列出一元二次方程求解即可;
(2)根据题意得到,根据函数的性质以及自变量的取值范围求函数最值.
【详解】(1)解:根据题意得,,
解得,,
当时,,符合题意;
当时,,不符合题意,舍去,
∴当的长为时,花圃的面积为;
(2)解:花圃的面积,
而由题意:,
即,
∵,
∴当时,y随x的增大而减小,
∴当时面积最大,最大面积为.
11.(1)
(2)每件产品售价定为65元时,日销售利润最大,最大利润是12250元.
(3)
【分析】本题考查了二次函数的实际应用,解题的关键是正确理解题意,根据题意列出函数表达式,熟练掌握二次函数的性质.
(1)根据“每件售价定为50元时,日销售量为500件,每件售价每提高元,日销售量减少5件”即可列出函数关系式;
(2)根据总利润=单件利润×数量,列出W关于x的函数关系式,再根据题意列出不等式组,求出x的取值范围,再结合二次函数的性质,即可解答;
(3)先求出时x的值,再结合二次函数的性质,以及(2)中得出x的取值范围,即可解答.
【详解】(1)解:由题意得:,
∴y与x之间的函数关系式为;
(2)解:由题意得
,
由题意得,
解得,
∵,
∴当时,W取得最大值,最大值为12250,
答:当每件产品售价定为65元时,日销售利润W(元)最大,最大利润是12250元;
(3)解:当元时,,
解得,
∵,
∴图象开口向下,
∴当时,,
又∵,
∴,
答:当日销售利润不低于6000元时,每件文创产品售价x的取值范围为.
12.(1)
(2)销售单价应定为每千克60元或70元
(3)当蟠桃售价每千克65元时,利润最大,最大利润是2500元
【分析】本题考查一次函数解析式,一元二次方程的实际应用,二次函数的实际应用.
(1)设y关于x的函数解析式为,根据当时,;当时,,利用待定系数法求解即可;
(2)根据利润销售量(售价进价)建立方程求解即可;
(3)设利润为,根据利润销售量(售价进价)建立函数关系式,利用二次函数的性质即可解答.
【详解】(1)解:设y关于x的函数解析式为,
根据题意得:,
解得:,
y关于x的函数解析式为;
(2)解:根据题意得:,即,
解得:,
答:销售单价应定为每千克60元或70元;
(3)解:设利润为,根据题意得:
,即,
,
,
当时,有最大值,最大值为,
答:当蟠桃售价每千克65元时,利润最大,最大利润是2500元.
13.(1)30元
(2);最大值160元
【分析】本题考查了分式方程的应用、二次函数的应用,正确列出分式方程,熟练掌握二次函数的性质是解此题的关键.
(1)设购进第一批“小金龙”每件进价为元,则购进第二批“小金龙”每件进价为元,根据“第二批所购数量是第一批购进数量的3倍”列出分式方程,解方程即可得出答案;
(2)由题意得得出与之间的函数关系式,利用二次函数的性质求解即可.
【详解】(1)解:设购进第一批“小金龙”每件进价为元,则购进第二批“小金龙”每件进价为元,
由题意得:,
解得:,
经检验,是原分式方程的根,且符合题意,
商场购进第一批“小金龙”每件的进价为30元.
(2)解:由题意得:,
当时,有最大值160元,
答:最大值为160元.
14.(1)秒时球离起点的高度是;
(2)秒或秒后球离起点的高度达到.
【分析】本题为二次函数实际应用问题,解答时注意将相应的函数值或自变量值代入函数关系式中求解即可.
(1)把代入即可求解;
(2)把代入求t即可.
【详解】(1)解:由题意,将分别代入函数关系式,
得,
当时,代入解得,
∴秒时球离起点的高度是;
(2)解:当时,,
解得.
故秒或秒后球离起点的高度达到.
15.(1)
(2)时,P的最大值为4418
【分析】此题主要考查了一次函数的应用以及二次函数的应用以及函数最值求法,得出关于的函数关系式是解题关键.
(1)直接利用待定系数法求一次函数解析式进而得出答案;
(2)根据计算公式为:车流量车流速度车流密度可得,再利用配方法求出最值即可.
【详解】(1)解:当时,.
当时,设,
由图象可知,,
解得:,
当时,;
(2)根据题意,得.
答:当车流密度为94辆千米时,车流量最大,为4418辆时.
16.(1)
(2)当销售单价定为元时,日获利w最大,最大利润为元
(3)
【分析】(1)设日销售量y与销售单价x之间的函数关系式,将,,代入得,,计算求解,进而可得结果;
(2)依题意得,,由,,可知当时,日获利w最大,最大利润为元;
(3)令,则,可求或,由,可得,由,可得.
【详解】(1)解:设日销售量y与销售单价x之间的函数关系式,
将,,代入得,,
解得,,
∴日销售量y与销售单价x之间的函数关系式;
(2)解:依题意得,,
∵,,
∴当时,日获利w最大,最大利润为元;
(3)解:令,则,
解得,或,
∵,
∴,
又∵,
∴.
【点睛】本题考查了一次函数的应用,二次函数的应用,二次函数的图象与性质,二次函数与一元二次方程的关系等知识.熟练掌握一次函数的应用,二次函数的应用,二次函数的图象与性质,二次函数与一元二次方程的关系是解题的关键.
17.(1);60
(2);第30天时,销售额W最大
(3)7
【分析】本题考查一次函数和二次函数的应用,解题的关键是读懂题意,列出函数关系式.
(1)用待定系数法可得,的值;
(2)由销售额,分两种情况可得函数关系式,再分别 根据函数值比较即可得答案;
(3)分两种情况,结合(2)可列出方程解得答案.
【详解】(1)解:把,代入得:
,
解得,
故答案为:,60;
(2)解:由(1)可得,
当时,;
当时,;
;
当,,
∵,
∴当时,W有最大值,最大值为800;
当时,,
∵,
∴W随x增大而增大,
∴时,W有最大值,最大值为,
∵,
∴第30天时,销售额W最大.
(3)解:在中,令得:,
整理得,
方程无实数解;
由得,
整数,
可取24,25,26,27,28,29,30,
销售额超过1000元的共有7天.
18.(1)钢笔的单价为元,笔记本的单价为元
(2)人
(3)一等奖人时,购买奖品的金额最少,最少金额为元
【分析】本题考查了二元一次方程组的应用、一元二次方程的应用以及二次函数的应用,
(1)设钢笔的单价为元,笔记本的单价为元,根据“购买支钢笔和本笔记本共元,购买支钢笔和本笔记本共元”,即可得出关于、的二元一次方程组,解之即可得出结论;
(2)设获得一等奖的人数为人,则获得二等奖的人数为人,钢笔的单价为元,根据购买奖品的金额为元,即可得出关于的一元二次方程,解之取其符合题意的值即可得出结论;
(3)设购买奖品的总金额为元,利用总价单价数量,即可得出关于的函数关系式,再利用二次函数的性质,即可解决最值问题;
解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)找准等量关系,正确列出一元二次方程;(3)根据各数量之间的关系,找出关于的函数关系式.
【详解】(1)解:设钢笔的单价为元,笔记本的单价为元,
依题意,得:,
解得:,
答:钢笔的单价为元,笔记本的单价为元;
(2)设获得一等奖人数为人,则获得二等奖人数为个,则钢笔的单价为元,
依题意,得:,
解得:,(舍去),
∴获得一等奖学生人数为人;
(3)设购买奖品的总金额为元,则,
即,
∵,
∴抛物线的开口向下,对称轴为,
∵,为整数,
∴当,随的增加而减小,
∴当,有最小值为元,
∴一等奖人时,购买奖品的金额最少,最少金额为元.
19.(1)
(2)销售利润为3000元时的销售量为300件
(3)当销售价格为18元时,这批产品获得的利润最大,最大利润是2880元
【分析】本题考查二次函数的应用、一元一次不等式的应用,解答的关键是读懂题意,列出函数关系式,运算二次函数性质解决问题.
(1)根据总利润等于单件利润乘以销售量列函数关系式即可;
(2)求出当时的x值即可;
(3)先配方,利用求二次函数的最值的方法求解即可.
【详解】(1)解:根据题意,,
即w与x的函数关系式为;
(2)解:当时,由得,
解得,
∴,
答:销售利润为3000元时的销售量为300件;
(3)解:,
∵销售量不能低于360件,
∴且,
∴,又,
∴当时,w最大,最大值为2880,
答:当销售价格为18元时,这批产品获得的利润最大,最大利润是2880元.
20.(1)
(2)当每间房价定为160元,宾馆的利润w最大为1960元
(3)这天每间房的定价是130元或190元
【分析】本题考查二次函数及一元二次方程的应用,解题的关键是读懂题意,列出函数关系式.
(1)根据当每个房间每天的定价每增加10元时,就会有一个房间空闲知:每间房间定价元时,每天有游客居住的房间数为;
(2)根据总利润每个房间利润房间数量可得,由二次函数性质可得答案;
(3)由该天利润为1870元,结合(2)可得,即可解得答案.
【详解】(1)解:根据题意知,每间房间定价元时,每天有游客居住的房间数为;
故答案为:;
(2)解:根据题意得:,
,
当时,取最大值,最大值为1960元;
答:当每间房价定为160元,宾馆的利润最大为1960元;
(3)解:该天利润为1870元,
,
解得或,
答:这天每间房的定价是130元或190元.
21.(1)销量为千克,利润为元;
(2)
(3)当时,有最大利润为元.
【分析】本题考查的是二次函数的实际应用,理解题意,确定正确的函数关系式是解本题的关键;
(1)根据“销售单价每涨1元,月销售量就减少100千克”,可知:月销售量(销售单价,再计算利润即可;
(2)根据总利润等于每千克的利润乘以销售量可得函数关系式;
(3)利用二次函数的性质可得二次函数的最值.
【详解】(1)解:∵按46元/销售,一个月可以售出4000,销售价每涨1元,月销量就会减少100.
∴销售单价定为55元时,每千克的利润为(元),
销售数量为:(千克),
∴销售利润为(元);
(2)由题意可得:月销售利润y与销售价之间的函数解析式为:
;
(3)∵
∵,
∴当时,有最大利润为元.
22.(1)每天生产A产品30件,B产品20件
(2)①或6;②
【分析】本题主要考查了二次函数的实际应用:
(1)设每天生产A产品x件,则每天生产B产品件,由题意列出方程可得答案;
(2)根据题意列出函数解析式,由二次函数的性质求最值.
【详解】(1)解:设每天生产A产品x件,则每天生产B产品件,
由题意得:,
解得:,
每天生产B产品为件;
答:每天生产A产品30件,B产品20件
(2)解:①由题意得:
令,则,
解得或6
②由题意得:
实际生产B产品的数量不少于A产品数量的1.2倍,
,
解得:
,且
当时,w随x的增大而减小,
取正整数,
当时,w有最大值,即.
23.(1)11700元
(2),城生产20件,城生产180件
(3)当时,从A城运往C地件,从B城运往C地130件,运往地50件,运费最小;时,从A城运往D地件,从B城运往C地150件,运往地30件,运费最小
【分析】本题考查二次函数的实际应用,一次函数的实际应用,找准等量关系,正确的列出函数关系式,是解题的关键.
(1)分别求出两城各自的总成本,相加即可;
(2)根据总成本等于两城各自的总成本之和,列出函数关系式,利用二次函数的性质,求出最值即可;
(3)设从A城运往C地件,总运费为元,列出一次函数,利用一次函数的性质进行求解即可.
【详解】(1)解:当A城生产产品的件数为30件时,则:B城生产产品的件数为件,
∵,
∴当时,,
∴A,B两城完成这种产品生产任务的总成本为元;
(2)由题意,得:,
∴,
∴当,即:城生产20件,城生产件时,总成本最低;
∴城生产20件,城生产180件;
(3)设从A城运往C地件,总运费为元,则从城运往地件,从B城运往C地件,运往地件,由题意,得:
,
∵且,
∴,
当,即时,随的增大而减下,
∴当时,最小为:;
此时从A城运往C地件,从B城运往C地130件,运往地50件,运费最小;
当,即时,随的增大而增大,
∴当时,最小为,
此时从A城运往D地件,从B城运往C地150件,运往地30件,运费最小.
24.(1)
(2)当销售单价定为90元/件时,每天的销售利润最大,最大利润是3600元
【分析】(1)根据销售单价为x元,则降价元,每件的盈利元,每天可售出件,根据题意,得,解得即可.
(2)根据,构造二次函数,根据抛物线的最值,解之即可得出x的值即可求得.
本题考查了一元二次方程的应用,二次函数的最值,最大利润问题,熟练掌握一元二次方程的应用,二次函数的最值是解题的关键.
【详解】(1)根据销售单价为x元,则降价元,
每件的盈利元,每天可售出件,
根据题意,得,
故.
(2)由(1)可得.
∵,,
∴当时,y取得最大值,最大值为3600.
答:当销售单价定为90元/件时,每天的销售利润最大,最大利润是3600元.
25.(1)(,且为整数)
(2)第天日销售利润最大,最大利润为元;第天日销售利润最小,最小利润为元
(3)利润不低于元的共有天
【分析】本题考查了二次函数的实际应用,熟练掌握二次函数的图象和性质是解题的关键.
(1)根据销售问题中的基本等量关系:销售利润=日销售量×(一件的销售价-一件的进价),建立函数关系式即可.
(2)将(1)中函数关系式配方,可得其顶点式,结合自变量的范围,根据二次函数的性质可得函数的最值情况.
(3)令,即,解得,因为,且x为整数,所以利润不低于元的共有天.
【详解】(1)解:根据题意,得
(,且为整数).
(2)∵,
∴当时,取最大值为元;
当时,取最小值为元.
故:第天日销售利润最大,最大利润为元;第天日销售利润最小,最小利润为元.
(3)令,即,
解得,
∵,且x为整数,
∴利润不低于元的共有天.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
同课章节目录
