人教版数学八年级上暑假预习课第十六讲 最短路径(含解析)
文档属性
| 名称 | 人教版数学八年级上暑假预习课第十六讲 最短路径(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-30 17:44:42 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版数学八年级上暑假预习课
第十六讲 最短路径
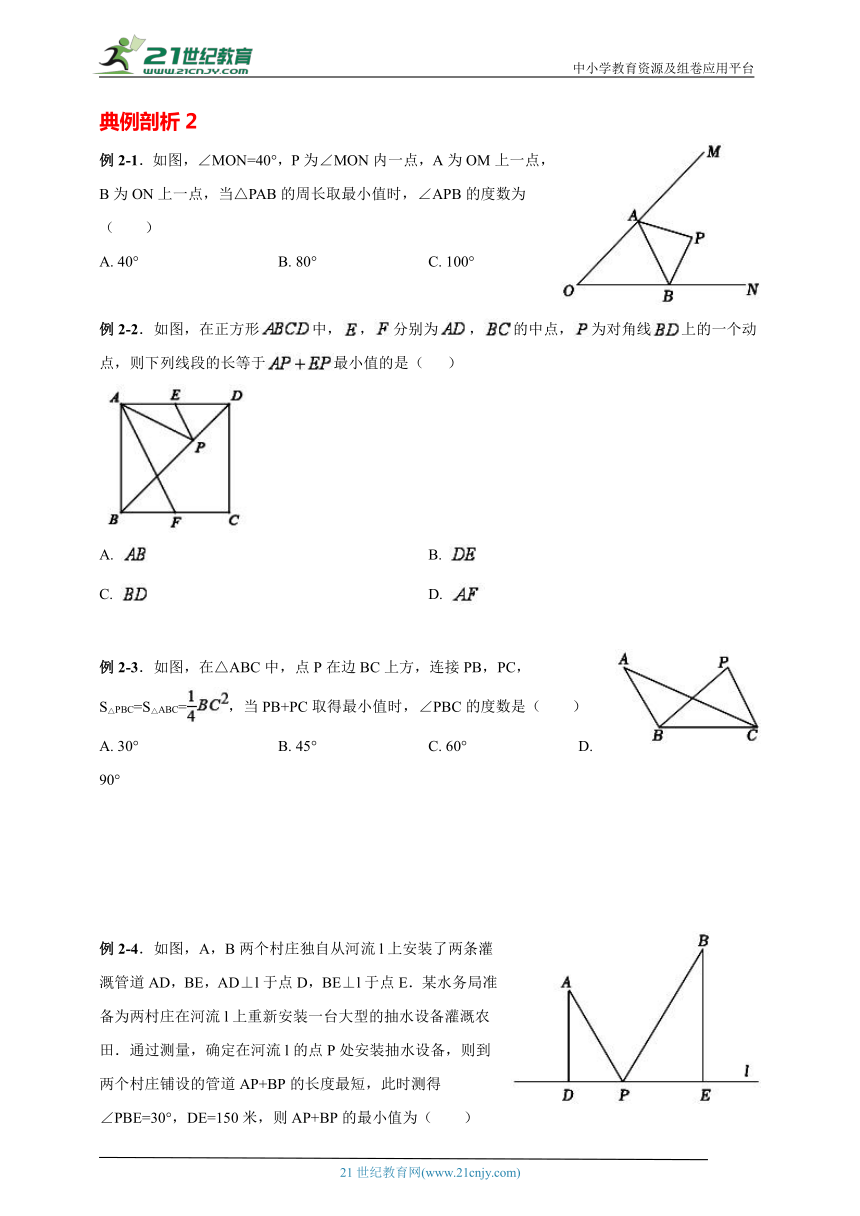
一、专题导航
二、知识点梳理
类型一、 垂直线段最短问题
方法技巧:一动点与一定点连成的线段中,若动点在定直线上,则垂线段最短。
典例剖析1
例1-1.如图,等腰三角形ABC底边BC的长为4 cm,面积为12 cm2,腰AB的垂直平分线EF交AB于点E,交AC于点F,若D为BC边上的中点,M为线段EF上一点,则△BDM的周长最小值为( )
A. 5 cm B. 6 cm C. 8 cm D. 10 cm
例1-2.如图,在△ABC中,AC=BC=8,∠ACB=120°,BD平分∠ABC交AC于点D,点E、F分别是线段BD,BC上的动点,则CE+EF的最小值是( )
A. 2 B. 4 C. 5 D. 6
例1-3.如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,∠ABC的平分线交AC于点D,点E,F分别是BD、AB上的动点,则AE+EF的最小值为( )
A. 2 B. 2.4 C. 2.5 D. 3
类型二、两点之间线段最短问题
定点关于定直线对称转化为两点之间线段最短求最值.
①两定一动
②一定两动
③两定两动
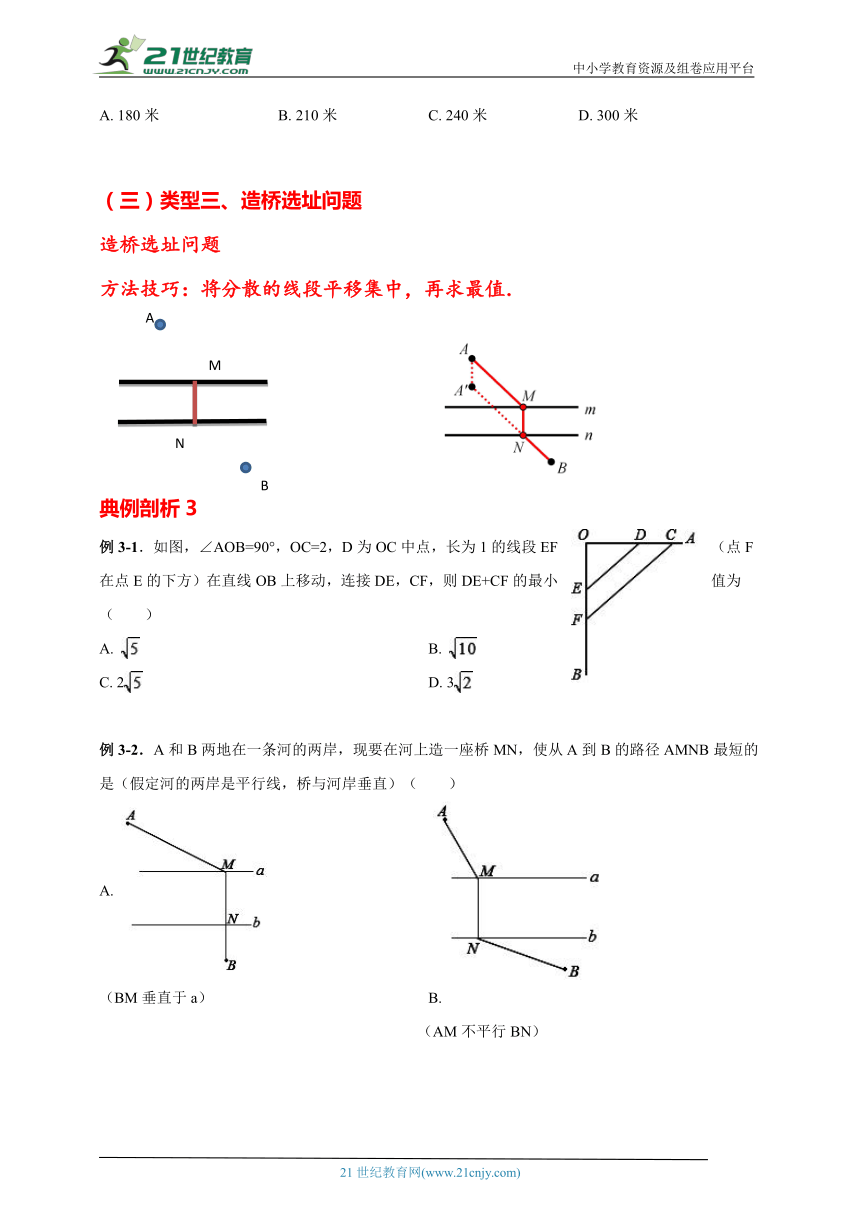
典例剖析2
例2-1.如图,∠MON=40°,P为∠MON内一点,A为OM上一点,B为ON上一点,当△PAB的周长取最小值时,∠APB的度数为( )
A. 40° B. 80° C. 100° D. 140°
例2-2.如图,在正方形中,,分别为,的中点,为对角线上的一个动点,则下列线段的长等于最小值的是( )
A. B.
C. D.
例2-3.如图,在△ABC中,点P在边BC上方,连接PB,PC,S△PBC=S△ABC=,当PB+PC取得最小值时,∠PBC的度数是( )
A. 30° B. 45° C. 60° D. 90°
例2-4.如图,A,B两个村庄独自从河流l上安装了两条灌溉管道AD,BE,AD⊥l于点D,BE⊥l于点E.某水务局准备为两村庄在河流l上重新安装一台大型的抽水设备灌溉农田.通过测量,确定在河流l的点P处安装抽水设备,则到两个村庄铺设的管道AP+BP的长度最短,此时测得∠PBE=30°,DE=150米,则AP+BP的最小值为( )
A. 180米 B. 210米 C. 240米 D. 300米
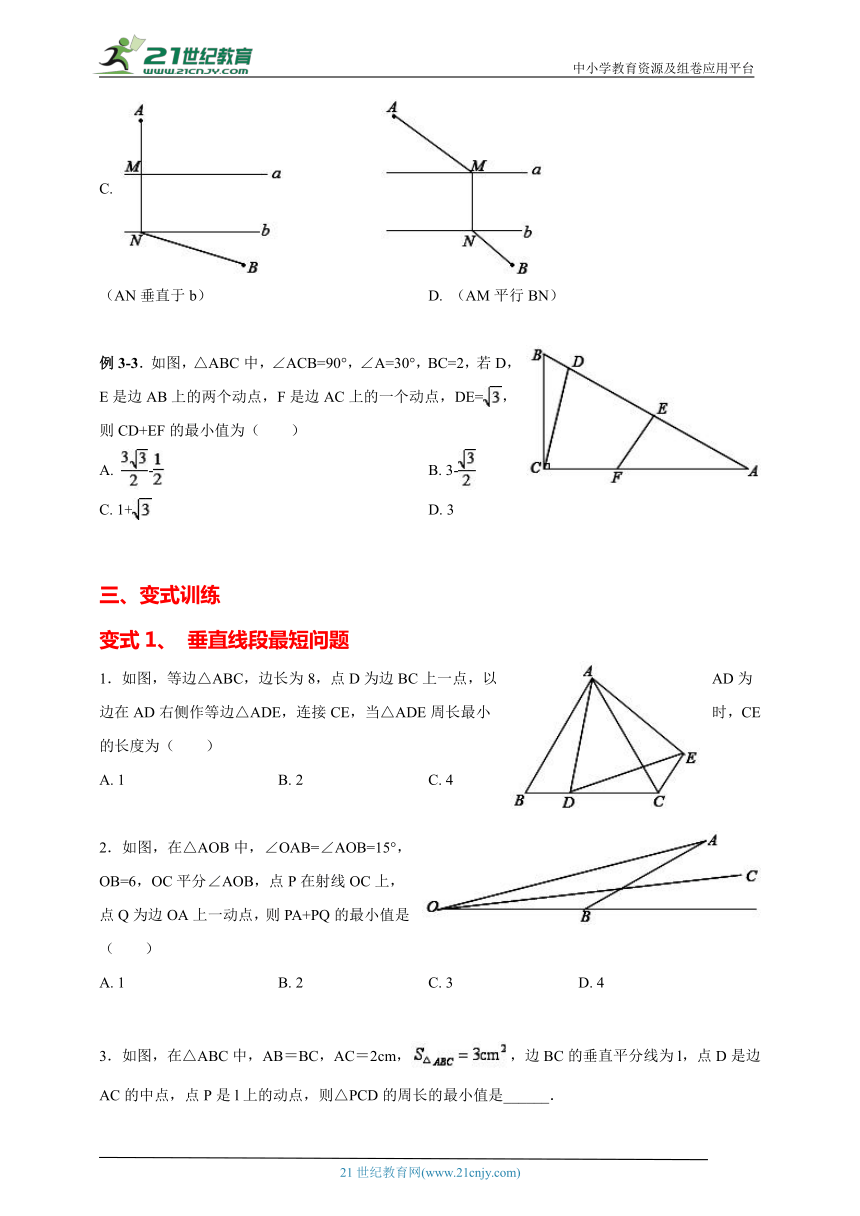
类型三、造桥选址问题
造桥选址问题
方法技巧:将分散的线段平移集中,再求最值.
典例剖析3
例3-1.如图,∠AOB=90°,OC=2,D为OC中点,长为1的线段EF(点F在点E的下方)在直线OB上移动,连接DE,CF,则DE+CF的最小值为( )
A. B.
C. 2 D. 3
例3-2.A和B两地在一条河的两岸,现要在河上造一座桥MN,使从A到B的路径AMNB最短的是(假定河的两岸是平行线,桥与河岸垂直)( )
A.
(BM垂直于a) B.
(AM不平行BN)
C.
(AN垂直于b) D. (AM平行BN)
例3-3.如图,△ABC中,∠ACB=90°,∠A=30°,BC=2,若D,E是边AB上的两个动点,F是边AC上的一个动点,DE=,则CD+EF的最小值为( )
A. - B. 3-
C. 1+ D. 3
变式训练
变式1、 垂直线段最短问题
1.如图,等边△ABC,边长为8,点D为边BC上一点,以AD为边在AD右侧作等边△ADE,连接CE,当△ADE周长最小时,CE的长度为( )
A. 1 B. 2 C. 4 D. 8
2.如图,在△AOB中,∠OAB=∠AOB=15°,OB=6,OC平分∠AOB,点P在射线OC上,点Q为边OA上一动点,则PA+PQ的最小值是( )
A. 1 B. 2 C. 3 D. 4
3.如图,在△ABC中,AB=BC,AC=2cm,,边BC的垂直平分线为l,点D是边AC的中点,点P是l上的动点,则△PCD的周长的最小值是______.
变式2、两点之间线段最短问题
1.现需要在某条街道l上修建一个核酸检测点P,向居住在A,B小区的居民提供核酸检测服务,要使P到A,B的距离之和最短,则核酸检测点P符合题意的是( )
A. B.
C. D.
2.如图,等边△ABC中,BD⊥AC于D,AD=3.5cm,点P、Q分别为AB、AD上的两个定点且BP=AQ=2cm,在BD上有一动点E使PE+QE最短,则PE+QE的最小值为( )
A. 3cm B. 4cm C. 5cm D. 6cm
3.如图,在锐角△ABC中,∠ACB=50°;边AB上有一定点P,M、N分别是AC和BC边上的动点,当△PMN的周长最小时,∠MPN的度数是( )
A. 50° B. 60° C. 70° D. 80°
4.如图,在平面直角坐标系xOy中,点A的坐标为(0,6),点B为x轴上一动点,以AB为边在直线AB的右侧作等边三角形ABC.若点P为OA的中点,连接PC,则PC的长的最小值为_____.
变式3、类型三、造桥选址问题
1.如图,矩形ABCD中,AB=4,BC=2,G是AD的中点,线段EF在边AB上左右滑动,若EF=1,则GE+CF的最小值为 _____.
2.如图所示,矩形ABCD中,AB=8,AD=4,点E是AD的中点,点F是AB上任意一点,沿着EF翻折,点A落在点G处,点H是CD上任意一点,连接HG和HB,则HG+HB的最小值为 _____.
3.如图,∠MON=15°,四边形ABCD的顶点A在∠MON的内部,B,C两点在OM上(C在B,O之间),且BC=1,点D在ON上,若当CD⊥OM时,四边形ABCD的周长最小,则此时AD的长度是_____.
能力提升
提升1、 垂直线段最短问题
1.如图,BD是△ABC的角平分线,E和F分别是AB和BD上的动点,已知△ABC的面积是12cm2,BC的长是8cm,则AF+EF的最小值是 _____cm.
2.如图,锐角△ABC中,BD是∠ABC的角平分线,M、N分别是BD、BC线段上运动的点,S△ABC=8,AB=4,则MN+MC的最小值是=_____.
3.如图,在Rt△ABC中,AB=6,∠BAC=30°,∠BAC的平分线交BC于点D,E,F分别是线段AD和AB上的动点,则BE+EF的最小值是_____.
提升2、两点之间线段最短问题
1.如图,等边△ABC中,BD⊥AC于D,QD=1.5,点P、Q分别为AB、AD上的两个定点且BP=AQ=2,在BD上有一动点E使PE+QE最短,则PE+QE的最小值为 _____.
2.如图,在△ABC中,AB=3,AC=4,BC=5,EF是BC的垂直平分线,P是直线EF上的任意一点,则PA+PB的最小值是 _____.
3.如图,A,B两个工厂位于一段直线形河的异侧,A厂距离河边AC=5km,B厂距离河边BD=1km,经测量CD=8km,现准备在河边某处(河宽不计)修一个污水处理厂E.
(1)设ED=x,请用x的代数式表示AE+BE的长;
(2)为了使两厂的排污管道最短,污水厂E的位置应怎样来确定此时需要管道多长?
(3)通过以上的解答,充分展开联想,运用数形结合思想,请你猜想的最小值为多少?
4.(1)小河的同旁有甲、乙两个村庄如图(1),现计划在河岸AB上建一个水泵站,向两村供水,用以解决村民生活用水问题.(保留作图痕迹)
①如果要求水泵站到甲、乙两村庄的距离相等,水泵站M应建在河岸AB上的何处?
②如果要求建造水泵站,供水管道使用建材最省,水泵站N又应建在河岸AB上的何处?
(2)如图(2),作出△ABC关于直线l的对称图形.
提升3、类型三、造桥选址问题
1.如图,A、B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A、B两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点.(保留作图痕迹)
2.如图,平行河岸两侧各有一城镇,,根据发展规划,要修建一条桥梁连接,两镇,已知相同长度造桥总价远大于陆上公路造价,为了尽量减少总造价,应该选择方案( )
A. B.
C. D.
3.在长方形ABCD中,AB=4,BC=8,点P、Q为BC边上的两个动点(点P位于点Q的左侧,P、Q均不与顶点重合),PQ=2
(1)如图①,若点E为CD边上的中点,当Q移动到BC边上的中点时,求证:AP=QE;
(2)如图②,若点E为CD边上的中点,在PQ的移动过程中,若四边形APQE的周长最小时,求BP的长;
(3)如图③,若M、N分别为AD边和CD边上的两个动点(M、N均不与顶点重合),当BP=3,且四边形PQNM的周长最小时,求此时四边形PQNM的面积.
人教版数学八年级上暑假预习课
第十六讲 最短路径(解析版)
一、专题导航
二、知识点梳理
类型一、 垂直线段最短问题
方法技巧:一动点与一定点连成的线段中,若动点在定直线上,则垂线段最短。
典例剖析1
例1-1.如图,等腰三角形ABC底边BC的长为4 cm,面积为12 cm2,腰AB的垂直平分线EF交AB于点E,交AC于点F,若D为BC边上的中点,M为线段EF上一点,则△BDM的周长最小值为( )
A. 5 cm B. 6 cm C. 8 cm D. 10 cm
【答案】C
【解析】连接AD,由于△ABC是等腰三角形,点D是BC边的中点,故AD⊥BC,再根据三角形的面积公式求出AD的长,再根据EF是线段AB的垂直平分线可知,点B关于直线EF的对称点为点A,故AD的长为BM+MD的最小值,由此即可得出结论.
如图,连接AD.
∵△ABC是等腰三角形,点D是BC边的中点,∴AD⊥BC,∴S△ABC=BC AD=×4×AD=12,解得:AD=6(cm).
∵EF是线段AB的垂直平分线,∴点B关于直线EF的对称点为点A,∴AD的长为BM+MD的最小值,∴△BDM的周长最短=(BM+MD)+BD=AD+BC=6+×4=6+2=8(cm).
故选C.
【点睛】本题考查的是轴对称﹣最短路线问题,熟知等腰三角形三线合一的性质是解答此题的关键.
例1-2.如图,在△ABC中,AC=BC=8,∠ACB=120°,BD平分∠ABC交AC于点D,点E、F分别是线段BD,BC上的动点,则CE+EF的最小值是( )
A. 2 B. 4 C. 5 D. 6
【答案】B
【解析】作C点关于BD的对称点C',过C'作C'F⊥BC交BD于点E,交BC于点F,CE+EF的最小值C'F的长.
解:作C点关于BD的对称点C',过C'作C'F⊥BC交BD于点E,交BC于点F,
∴CE+EF=C'E+EF≥C'F,
∴CE+EF的最小值C'F的长,
∴CC'⊥BD,
∵BD平分∠ABC,
∴∠C'BG=∠GBC,
在△C'BG和△CBG中,
,
∴△C'BG≌△CBG(ASA),
∴BC=BC',
∵AC=BC=8,∠ACB=120°,
∴∠ABC=30°,BC'=8,
在Rt△BFC'中,C'F=BC' sin30°=8×=4,
∴CE+EF的最小值为4,
故选:B.
例1-3.如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,∠ABC的平分线交AC于点D,点E,F分别是BD、AB上的动点,则AE+EF的最小值为( )
A. 2 B. 2.4 C. 2.5 D. 3
【答案】B
【解析】作点A关于BD的对称点M,过M作MF⊥AB于F,交BD于E,则AE+EF的最小值是MF的长.由MF∥CA可得,进而可得答案.
解:作点A关于BD的对称点M,
∵BD平分∠ABC,
∴M落在BC上.
∴BM=BA=4,
过M作MF⊥AB于F,交BD于E,
则AE+EF的最小值是MF的长.
∵∠MFB=∠CAB=90°,
∴MF∥CA,
∴,
即,MF=2.4,
∴AE+EF=MF=2.4.
故选:B.
类型二、两点之间线段最短问题
定点关于定直线对称转化为两点之间线段最短求最值.
①两定一动
②一定两动
③两定两动
典例剖析2
例2-1.如图,∠MON=40°,P为∠MON内一点,A为OM上一点,B为ON上一点,当△PAB的周长取最小值时,∠APB的度数为( )
A. 40° B. 80° C. 100° D. 140°
【答案】C
【解析】如图,作P点关于OM、ON的对称点P1,P2,PP1与OM交点为C,PP2与ON交点为D,连接P1P2交OM、ON于A、B两点,则∠P1PA=∠P1,∠P2PB=∠P2,由题意知,当P1,A,B,P2四点共线时,△PAB的周长最小,由PP1⊥OM,PP2⊥ON,可知∠PCO=∠PDO=90°,∠P1PP2=360°-∠PCO-∠PDO-∠MON=140°,则∠P1PA+∠P2PB=∠P1+∠P2=180°-∠P1PP2=40°,根据∠APB=∠P1PP2-(∠P1PA+∠P2PB),计算求解即可.
解:如图,作P点关于OM、ON的对称点P1,P2,PP1与OM交点为C,PP2与ON交点为D,连接P1P2交OM、ON于A、B两点,则∠P1PA=∠P1,∠P2PB=∠P2,
由题意知,当P1,A,B,P2四点共线时,△PAB的周长最小,
∵PP1⊥OM,PP2⊥ON,
∴∠PCO=∠PDO=90°,
∴∠P1PP2=360°-∠PCO-∠PDO-∠MON=140°,
∴∠P1PA+∠P2PB=∠P1+∠P2=180°-∠P1PP2=40°,
∴∠APB=∠P1PP2-(∠P1PA+∠P2PB)=100°,
故选:C.
例2-2.如图,在正方形中,,分别为,的中点,为对角线上的一个动点,则下列线段的长等于最小值的是( )
A. B.
C. D.
【答案】D
【解析】连接,当点,,在同一直线上时,的最小值为长,依据,即可得到最小值等于线段的长.
解:如图,连接,
由,,,
可得,
,
,
当点,,在同一直线上时,
的最小值为长,
此时,由,,,
可得,
,
最小值等于线段的长,
故选:D.
【点睛】本题考查的是轴对称,最短路线问题,解题的关键是根据题意作出关于的对称点.
例2-3.如图,在△ABC中,点P在边BC上方,连接PB,PC,S△PBC=S△ABC=,当PB+PC取得最小值时,∠PBC的度数是( )
A. 30° B. 45° C. 60° D. 90°
【答案】B
【解析】由三角形面积关系得出AP与BC平行,AP与BC的距离为BC,作点B关于直线AP的对称点B',连接B'C交AP于P′,则BB'⊥AP,P′B=P′B',此时点P′到B、C两点距离之和最小,证明△BB'C是等腰直角三角形,即可得出答案.
解:如图,连接AP,
∵S△PBC=S△ABC==BC BC,
∴AP∥BC平行,AP与BC的距离为BC,
作B点关于AP的对称点B',连接B'C,交AP于P′点,连接P'B,
由对称性可知,B'P′=BP′,
∴PB+PC=B'P′+P′C=B'C,此时PB+PC最小,
∵BB'=BC,
∴△BCB'是等腰直角三角形,
∴∠B'CB=∠B'=45°,
∴∠B'BP′=45°,
∴∠P′BC=45°,
∴当PB+PC取得最小值时,∠PBC的度数是45°.
故选:B.
例2-4.如图,A,B两个村庄独自从河流l上安装了两条灌溉管道AD,BE,AD⊥l于点D,BE⊥l于点E.某水务局准备为两村庄在河流l上重新安装一台大型的抽水设备灌溉农田.通过测量,确定在河流l的点P处安装抽水设备,则到两个村庄铺设的管道AP+BP的长度最短,此时测得∠PBE=30°,DE=150米,则AP+BP的最小值为( )
A. 180米 B. 210米 C. 240米 D. 300米
【答案】D
【解析】延长AD到点F,使FD=AD,连接FP,则点F与点A关于直线l对称,所以FP=AP,则AP+BP=FP+BP,则AP+BP最短,可知FP+BP最短,则F、P、B三点在同一直线上,所以∠A=∠F=∠PBE=30°,则AP=2PD,BP=2PE,AP+BP=2DE=300米,于是得到问题的答案.
解:延长AD到点F,使FD=AD,连接FP,
∵AD⊥l,
∴点F与点A关于直线l对称,
∴FP=AP,
∴AP+BP=FP+BP,
∵AP+BP最短,
∴FP+BP最短,
∴F、P、B三点在同一直线上,
∵BE⊥l,
∴AD∥BE,∠ADP=∠BEP=90°,
∴∠A=∠F=∠PBE=30°,
∴AP=2PD,BP=2PE,
∴AP+BP=2(PD+PE)=2DE=2×150=300(米),
∴AP+BP的最小值为300米,
故选:D.
类型三、造桥选址问题
造桥选址问题
方法技巧:将分散的线段平移集中,再求最值.
典例剖析3
例3-1.如图,∠AOB=90°,OC=2,D为OC中点,长为1的线段EF(点F在点E的下方)在直线OB上移动,连接DE,CF,则DE+CF的最小值为( )
A. B.
C. 2 D. 3
【答案】B
【解析】如图,作点D关于OB的对称点T,作TR∥OB,使得TR=EF,连接CR交OB于F,在FO的延长线上,取点E,使得EF=1,连接ET.DE,此时DE+CF的值最小.
解:如图,作点D关于OB的对称点T,作TR∥OB,使得TR=EF,连接CR交OB于F,在FO的延长线上,取点E,使得EF=1,连接ET.DE,此时DE+CF的值最小.
∵RT=EF=1,RT∥EF,
∴四边形TRFE是平行四边形,
∴ET=FR,
∵D,T关于OB对称,
∴ED=ET,
∴DE=RF,
∴DE+CF=RF+FC=RC,此时CR的值最小,最小值===,
故选:B.
例3-2.A和B两地在一条河的两岸,现要在河上造一座桥MN,使从A到B的路径AMNB最短的是(假定河的两岸是平行线,桥与河岸垂直)( )
A.
(BM垂直于a) B.
(AM不平行BN)
C.
(AN垂直于b) D. (AM平行BN)
【答案】D
【解析】过A作河的垂线AH,要使最短,MN⊥直线a,AI=MN,连接BI即可得出N,作出AM、MN、BN即可.
解:根据垂线段最短,得出MN是河的宽时,MN最短,即MN⊥直线a(或直线b),只要AM+BN最短即可,
即过A作河岸a的垂线AH,垂足为H,在直线AH上取点I,使AI等于河宽.
连接IB交河的b边岸于N,作MN垂直于河岸交a边的岸于M点,所得MN即为所求.
故选:D.
例3-3.如图,△ABC中,∠ACB=90°,∠A=30°,BC=2,若D,E是边AB上的两个动点,F是边AC上的一个动点,DE=,则CD+EF的最小值为( )
A. - B. 3-
C. 1+ D. 3
【答案】B
【解析】首先△ABC是含有30°角的直角三角形,因此可以得知各边的长分别为AB=4,AC=2.因为D,E是边AB上的两个动点,F是边AC上的一个动点,求CD+EF的最小值,就是需要转换成同一直线上求解,即求C关于AB的对称点C1,作C1C2∥AB.构建平行四边形C1DEC2,作C2F⊥AC于F,交AB于E.利用平行四边形和对称图形的性质,找出线段之间的关系.
解:如图,过C作AB的对称点C1,连接CC1,交AB于N;过C1作C1C2∥AB,且C1C2=,过C2作C2F⊥AC于F,交AB于E,C2F的长度即为所求最小值,
∵CC2∥DE,CC2=DE,
∴四边形C1DEC2是平行四边形,
∴C1D=C2E,
又∵C、C1关于AB对称,
∴CD=C1D,
∴CD+EF=C2F,
∵∠A=30°,∠ACB=90°,
∴AC=BC=2,
∴CN=,AN=3,
过C2作C2M⊥AB,则C2M=C1N=CN=,
∴C2M∥C1N,C1C2∥MN,
∴MN=C1C2=,
∵∠MEC2=∠AEF,∠AFE=∠C2ME=90°,
∴∠MC2E=∠A=30°,
在Rt△C2ME中,ME=1,C2M=,C2E=2,
∴AE=AN-MN-ME=3--1=2-,
∴EF=1-,
∴C2F=2+1-=3-.
故选:B.
变式训练
变式1、 垂直线段最短问题
1.如图,等边△ABC,边长为8,点D为边BC上一点,以AD为边在AD右侧作等边△ADE,连接CE,当△ADE周长最小时,CE的长度为( )
A. 1 B. 2 C. 4 D. 8
【答案】C
【解析】由等边三角形的性质得C△ADE=3AD,当△ADE周长最小时,AD⊥BC时,AD最小,利用全等三角形的判定边角边得△ABD和△ACE全等,即得CE的长度.
解:
∵△ADE是等边三角形,
∴AD=DE=AE,
∴C△ADE=3AD,
当△ADE周长最小时,
即AD最小,
当AD⊥BC时,AD最小,
此时,BD=AB sin30°=4,
∵△ABC是等边三角形,
∴∠1+∠2=60°,
又∵∠2+∠3=60°,
∴∠1=∠3,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE=4,
故选:C.
2.如图,在△AOB中,∠OAB=∠AOB=15°,OB=6,OC平分∠AOB,点P在射线OC上,点Q为边OA上一动点,则PA+PQ的最小值是( )
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】作AH⊥OB于H.交OC于P,作PQ⊥OA于Q,可得PA+PQ=PA+PH=AH,根据垂线段最短,PA+PQ最小值为AH,
解:作AH⊥OB于H,交OC于P,作PQ⊥OA于Q,
∵∠OAB=∠AOB=15°,
∴PH=PQ,
∴PA+PQ=PA+PH=AH,
∴PA+PQ的最小值为AH,
在Rt△ABH中,∵OB=AB=6,∠ABH=30°,
∴AH=AB=3,
∴PA+PQ的最小值为3,
故选:C.
3.如图,在△ABC中,AB=BC,AC=2cm,,边BC的垂直平分线为l,点D是边AC的中点,点P是l上的动点,则△PCD的周长的最小值是______.
【答案】4
【解析】连接BD,由于AB=BC,点D是AC边的中点,故BD⊥AC,再根据三角形的面积公式求出BD的长,再根据直线l是线段BC的垂直平分线可知,点C关于直线l的对称点为点B,故BD的长为CP+PD的最小值,由此即可得出结论.
解:连接BD,
∵AB=BC,点D是BC边的中点,
∴BD⊥AC,
∴S△ABC=AC BD=×2×BD=3,
解得BD=3,
∵直线l是线段BC的垂直平分线,
∴点C关于直线l的对称点为点B,
∴AB的长为CP+PD的最小值,
∴△CDP的周长最短=(CP+PD)+CD=BD+AC=3+1=4.
故答案为:4.
【点睛】本题考查的是轴对称-最短路线问题,熟知等腰三角形三线合一的性质是解答此题的关键.
变式2、两点之间线段最短问题
1.现需要在某条街道l上修建一个核酸检测点P,向居住在A,B小区的居民提供核酸检测服务,要使P到A,B的距离之和最短,则核酸检测点P符合题意的是( )
A. B.
C. D.
【答案】A
【解析】作A点关于直线l的对称点,连接对称点和点B交l于点P,进而根据轴对称性质解答即可.
解:作A点关于直线l的对称点,连接对称点和点B交l于点P,P即为所求.
故选:A.
2.如图,等边△ABC中,BD⊥AC于D,AD=3.5cm,点P、Q分别为AB、AD上的两个定点且BP=AQ=2cm,在BD上有一动点E使PE+QE最短,则PE+QE的最小值为( )
A. 3cm B. 4cm C. 5cm D. 6cm
【答案】C
【解析】作点Q关于BD的对称点Q′,连接PQ′交BD于E,连接QE,此时PE+EQ的值最小.最小值PE+EQ=PE+EQ′=PQ′.
解:如图,∵△ABC是等边三角形,
∴BA=BC,
∵BD⊥AC,
∴AD=DC=3.5cm,
作点Q关于BD的对称点Q′,连接PQ′交BD于E,连接QE,此时PE+EQ的值最小.最小值PE+EQ=PE+EQ′=PQ′,
∵AQ=2cm,AD=DC=3.5cm,
∴QD=DQ′=1.5(cm),
∴CQ′=BP=2(cm),
∴AP=AQ′=5(cm),
∵∠A=60°,
∴△APQ′是等边三角形,
∴PQ′=PA=5(cm),
∴PE+QE的最小值为5cm.
故选:C.
3.如图,在锐角△ABC中,∠ACB=50°;边AB上有一定点P,M、N分别是AC和BC边上的动点,当△PMN的周长最小时,∠MPN的度数是( )
A. 50° B. 60° C. 70° D. 80°
【答案】D
【解析】根据对称的性质,易求得∠C+∠EPF=180°,由∠ACB=50°,易求得∠D+∠G=50°,继而求得答案.
解:作点P关于AC,BC的对称点D,G,连接PD,PG分别交AC,BC于E,F,连接DG交AC于M,交BC于N,连接PM,PN.此时△PMN的周长最小.
∵PD⊥AC,PG⊥BC,
∴∠PEC=∠PFC=90°,
∴∠C+∠EPF=180°,
∵∠C=50°,
∴∠EPF=130°,
∵∠D+∠G+∠EPF=180°,
∴∠D+∠G=50°,
由对称可知:∠G=∠GPN,∠D=∠DPM,
∴∠GPN+∠DPM=50°,
∴∠MPN=130°-50°=80°,
故选:D.
4.如图,在平面直角坐标系xOy中,点A的坐标为(0,6),点B为x轴上一动点,以AB为边在直线AB的右侧作等边三角形ABC.若点P为OA的中点,连接PC,则PC的长的最小值为_____.
【答案】
【解析】以AP为边作等边三角形APE,连接BE,过点E作EF⊥AP于F,由“SAS”可证△ABE≌△ACP,可得BE=PC,则当BE有最小值时,PC有最小值,即可求解.
解:如图,以AP为边作等边三角形APE,连接BE,过点E作EF⊥AP于F,
∵点A的坐标为(0,6),
∴OA=6,
∵点P为OA的中点,
∴AP=3,
∵△AEP是等边三角形,EF⊥AP,
∴AF=PF=,AE=AP,∠EAP=∠BAC=60°,
∴∠BAE=∠CAP,
在△ABE和△ACP中,
∴△ABE≌△ACP(SAS),
∴BE=PC,
∴当BE有最小值时,PC有最小值,
即BE⊥x轴时,BE有最小值,
∴BE的最小值为OF=OP+PF=3+=,
∴PC的最小值为,
故答案为.
【点睛】本题考查了轴对称 最短路线问题,全等三角形的判定和性质,等边三角形的判定和性质,添加恰当辅助线构造全等三角形是本题的关键.
变式3、类型三、造桥选址问题
1.如图,矩形ABCD中,AB=4,BC=2,G是AD的中点,线段EF在边AB上左右滑动,若EF=1,则GE+CF的最小值为 _____.
【答案】3
【解析】解法一:利用已知可以得出GC,EF长度不变,求出GE+CF最小时即可得出四边形CGEF周长的最小值,利用轴对称得出E,F位置,即可求出.
解法二:设AE=x,则BF=3-x,根据勾股定理可得:EG+CF=+,由勾股定理构建另一矩形EFGH,根据线段的性质:两点之间线段最短可得结论.
解:解法一:如图,作G关于AB的对称点G',在CD上截取CH=1,然后连接HG'交AB于E,在EB上截取EF=1,此时GE+CF的值最小,
∵CH=EF=1,CH∥EF,
∴四边形EFCH是平行四边形,
∴EH=CF,
∴G'H=EG'+EH=EG+CF,
∵AB=4,BC=AD=2,G为边AD的中点,
∴DG'=AD+AG'=2+1=3,DH=4-1=3,
由勾股定理得:HG'==3,
即GE+CF的最小值为3.
解法二:∵AG=AD=1,
设AE=x,则BF=AB-EF-AE=4-x-1=3-x,
由勾股定理得:EG+CF=+,
如图,矩形EFGH中,EH=3,GH=2,GQ=1,
P为FG上一动点,设PG=x,则FP=3-x,
∴EP+PQ=+,
当E,P,Q三点共线时,EP+PQ最小,最小值是3,
即EG+CF的最小值是3.
故答案为:3.
2.如图所示,矩形ABCD中,AB=8,AD=4,点E是AD的中点,点F是AB上任意一点,沿着EF翻折,点A落在点G处,点H是CD上任意一点,连接HG和HB,则HG+HB的最小值为 _____.
【答案】8
【解析】作点B关于CD的对称点B',连接B'G,交CD于点H.则HB=HB',则HG+HB=HG+HB',其最小值为B'G的长,点G在以点E为圆心,2为半径的圆周上运动,所以EG+GB'的最小值为EB',因此B'G的最小值为:B'E-2.
解:作点B关于CD的对称点B',连接B'G,交CD于点H.
则HB=HB',
则HG+HB=HG+HB',其最小值为B'G的长.
∵AD=4,点E是AD的中点,
∴AE=DE=GE=2,
∴点G在以点E为圆心,2为半径的圆周上运动,
∵EG+GB'≥EB',
∴EG+GB'的最小值为EB',
∵EG=2,
∴B'G的最小值为:B'E-2.
在RtΔB'ME中,
EM=2+4=6,B'M=8,
B'E==10.
∴B'G的最小值为:B'E-2=10-2=8.
即HG+HB最小值为8.
故答案为:8.
3.如图,∠MON=15°,四边形ABCD的顶点A在∠MON的内部,B,C两点在OM上(C在B,O之间),且BC=1,点D在ON上,若当CD⊥OM时,四边形ABCD的周长最小,则此时AD的长度是_____.
【答案】2
【解析】根据最短问题解决的方法,分别作A关于OM,ON的对称点,提供连接对称点,列出四边形周长公式,根据已知条件,要使得四边形ABCD的周长最短,只需要四点共线,然后解直角三角形求出AD即可.
解:如图1中,分别作点A关于直线OM,ON的对称点A1,A2,连接BA1,DA2,过点A1作A1A3⊥CD于A3,
由图可知:AQ=A1Q=A3C,AB>AQ,当A,B,A1共线时,AB最短,此时A3C=AB,
∵四边形ABCD的周长=AB+BC+CD+AD=A3C+CD+DA2+BC=A3C+CD+DA2+1,
∴当A3,C,D,A2共线时,四边形ABCD的周长最短(如图2中),作AH⊥CD于H.
∵∠MON=15°,CD⊥OM,
∴∠ODC=90°-15°=75°,
∴∠FDA2=∠ODC=∠ADF=75°,
∴∠ADH=180°-75°-75°=30°,
在Rt△ADH中,AD===2.
故答案为2.
能力提升
提升1、 垂直线段最短问题
1.如图,BD是△ABC的角平分线,E和F分别是AB和BD上的动点,已知△ABC的面积是12cm2,BC的长是8cm,则AF+EF的最小值是 _____cm.
【答案】3
【解析】作E关于BD的对称点G,连接FG,过点A作AH⊥BC于H,将AF+EF转化AF+FG,由点到直线垂线段最短的AF+FG最小值为AH的长,由△ABC的面积是12cm2,BC的长是8cm,求出AH即可.
解:作E关于BD的对称点G,连接FG,过点A作AH⊥BC于H,
∵BD是△ABC的角平分线,
∴G必在BC上,
∵E、G关于BD对称,
∴EF=FG,
∴AF+EF=AF+FG,
∵点F在垂线段AH上最短,
∴AF+FG最小值为AH的长,
∵△ABC的面积是12cm2,BC的长是8cm,
∴×BC AH=12,
∴AH=3cm,
∴AF+EF的最小值是3cm,
故答案为:3.
2.如图,锐角△ABC中,BD是∠ABC的角平分线,M、N分别是BD、BC线段上运动的点,S△ABC=8,AB=4,则MN+MC的最小值是=_____.
【答案】4
【解析】作N点关于BD的对称点N',连接CN',过C作CE⊥AB交于点E,则N'必在AB上,NM+CM=MN'+CN=CN'≥CE,由S△ABC=8,AB=4,可求EC=4,即MN+MC的最小值是4.
解:作N点关于BD的对称点N',连接CN',过C作CE⊥AB交于点E,
∵BD是∠ABC的角平分线,
∴N'必在AB上,
∴NM+CM=MN'+CN=CN'≥CE,
∴当CN'=CE时,MN+MC的值最小,
∵S△ABC=8,AB=4,
∴EC=4,
∴MN+MC的最小值是4,
故答案为4.
3.如图,在Rt△ABC中,AB=6,∠BAC=30°,∠BAC的平分线交BC于点D,E,F分别是线段AD和AB上的动点,则BE+EF的最小值是_____.
【答案】3
【解析】作BH⊥AC交AD于点E,作EF⊥AB于F,根据角平分线的性质可得EH=EF,即可求得BE+EF=BH,根据H是与B点的距离最短的点,即为BH最短即可解题.
解:作BH⊥AC交AD于点E,作EF⊥AB于F,
∵AD平分∠BAC,EH⊥AC,EF⊥AB,
∴EF=EH,
∴BE+EF=BE+EH=BH,
∵H是与B点的距离最短的点,即为BH最短,
∴BE+EF最短为BH,
∵AB=6,∠BAC=30°,
∴BH=AB=3,
故答案为 3.
提升2、两点之间线段最短问题
1.如图,等边△ABC中,BD⊥AC于D,QD=1.5,点P、Q分别为AB、AD上的两个定点且BP=AQ=2,在BD上有一动点E使PE+QE最短,则PE+QE的最小值为 _____.
【答案】5
【解析】作点Q关于BD的对称点Q′,连接PQ′交BD于E,连接QE,此时PE+EQ的值最小.最小值PE+PQ=PE+EQ′=PQ′.
解:如图,∵△ABC是等边三角形,
∴BA=BC,
∵BD⊥AC,AQ=2,QD=1.5,
∴AD=DC=AQ+QD=3.5,
作点Q关于BD的对称点Q′,连接PQ′交BD于E,连接QE,此时PE+EQ的值最小.最小值PE+QE=PE+EQ′=PQ′,
∵AQ=2,AD=DC=3.5,
∴QD=DQ′=1.5,
∴CQ′=BP=2,
∴AP=AQ′=5,
∵∠A=60°,
∴△APQ′是等边三角形,
∴PQ′=PA=5,
∴PE+QE的最小值为5.
故答案为:5.
2.如图,在△ABC中,AB=3,AC=4,BC=5,EF是BC的垂直平分线,P是直线EF上的任意一点,则PA+PB的最小值是 _____.
【答案】4
【解析】根据线段的垂直平分线的性质可得BE=EC,根据两点之间线段最短即可求解.
解:如图,连接BP,
∵EF是BC的垂直平分线,
∴BP=CP,
根据两点之间线段最短,
∴PA+PB=PA+PC=AC,
∴PA+PB的最小值即为AC的长为4.
∴PA+PB的最小值为4.
故答案为:4.
3.如图,A,B两个工厂位于一段直线形河的异侧,A厂距离河边AC=5km,B厂距离河边BD=1km,经测量CD=8km,现准备在河边某处(河宽不计)修一个污水处理厂E.
(1)设ED=x,请用x的代数式表示AE+BE的长;
(2)为了使两厂的排污管道最短,污水厂E的位置应怎样来确定此时需要管道多长?
(3)通过以上的解答,充分展开联想,运用数形结合思想,请你猜想的最小值为多少?
【解析】(1)依据ED=x,AC⊥CD、BD⊥CD,故根据勾股定理可用x表示出AE+BE的长;
(2)根据两点之间线段最短可知连接AB与CD的交点就是污水处理厂E的位置.过点B作BF⊥AC于F,构造出直角三角形,利用勾股定理求出AB的长;
(3)根据AE+BE=可作出图形,当A、E、B共线时,利用勾股定理求出AB的值即可.
解:(1)在Rt△ACE和Rt△BDE中,根据勾股定理可得AE=,BE=,
∴AE+BE=+,
(2)根据两点之间线段最短可知,连接AB与CD的交点就是污水处理厂E的位置.
过点B作BF⊥AC于F,则有BF=CD=8,BD=CF=1.
∴AF=AC+CF=6.
在Rt△ABF中,BA=,
∴此时最少需要管道10km.
(3)根据以上推理,可作出下图,设ED=x,BD=3,CD=15,AC=5,当A、E、B共线时,求出AB的值即为原式的最小值.
在Rt△ABF中,AF=8,BF=CD=15,
由勾股定理可得:AB=,
∴的最小值为17.
4.(1)小河的同旁有甲、乙两个村庄如图(1),现计划在河岸AB上建一个水泵站,向两村供水,用以解决村民生活用水问题.(保留作图痕迹)
①如果要求水泵站到甲、乙两村庄的距离相等,水泵站M应建在河岸AB上的何处?
②如果要求建造水泵站,供水管道使用建材最省,水泵站N又应建在河岸AB上的何处?
(2)如图(2),作出△ABC关于直线l的对称图形.
【解析】(1)①利用线段的垂直平分线的性质解决问题即可.
②利用轴对称解决最短问题即可.
(2)分别作出A,B,C关于直线l的对称点A′,B′,C′即可.
解:(1)①如图(1)中,点E即为所求.
②如图(1)-1中,点E即为所求.
(2)如图(2)中,△A′B′C′即为所求.
提升3、类型三、造桥选址问题
1.如图,A、B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A、B两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点.(保留作图痕迹)
【解析】根据两点间线段最短可知作点A关于直线a对称的点C,连接BC交a于点P,则点P就是抽水站的位置.
解:作点A关于直线a对称的点C,连接BC交a于点P,则点P就是抽水站的位置.
2.如图,平行河岸两侧各有一城镇,,根据发展规划,要修建一条桥梁连接,两镇,已知相同长度造桥总价远大于陆上公路造价,为了尽量减少总造价,应该选择方案( )
A. B.
C. D.
【答案】C
【分析】作PP'垂直于河岸L,使PP′等于河宽,连接QP′,与河岸L相交于N,作NM⊥L,根据平行线的判定与性质,易证得此时PM+NQ最短.
【详解】解:如图,作PP'垂直于河岸L,使PP′等于河宽,连接QP′,与河岸L相交于N,作NM⊥L,则MN∥PP′且MN=PP′,于是四边形PMNP′为平行四边形,故PM=NP′.根据“两点之间线段最短”,QP′最短,即PM+NQ最短.观察选项,选项C符合题意.
故选C.
【点睛】本题主要考查最短路径问题,解此题的关键在于熟练掌握其知识点.
3.在长方形ABCD中,AB=4,BC=8,点P、Q为BC边上的两个动点(点P位于点Q的左侧,P、Q均不与顶点重合),PQ=2
(1)如图①,若点E为CD边上的中点,当Q移动到BC边上的中点时,求证:AP=QE;
(2)如图②,若点E为CD边上的中点,在PQ的移动过程中,若四边形APQE的周长最小时,求BP的长;
(3)如图③,若M、N分别为AD边和CD边上的两个动点(M、N均不与顶点重合),当BP=3,且四边形PQNM的周长最小时,求此时四边形PQNM的面积.
【答案】(1)见解析; (2) 4; (3) 4
【分析】(1)由“SAS”可证△ABP≌△QCE,可得AP=QE;
(2)要使四边形APQE的周长最小,由于AE与PQ都是定值,只需AP+EQ的值最小即可.为此,先在BC边上确定点P、Q的位置,可在AD上截取线段AF=DE=2,作F点关于BC的对称点G,连接EG与BC交于一点即为Q点,过A点作FQ的平行线交BC于一点,即为P点,则此时AP+EQ=EG最小,然后过G点作BC的平行线交DC的延长线于H点,那么先证明∠GEH=45°,再由CQ=EC即可求出BP的长度;
(3)要使四边形PQNM的周长最小,由于PQ是定值,只需PM+MN+QN的值最小即可,作点P关于AD的对称点F,作点Q关于CD的对称点H,连接FH,交AD于M,交CD于N,连接PM,QN,此时四边形PQNM的周长最小,由面积和差关系可求解.
(1)解:证明:∵四边形ABCD是矩形,
∴CD=AB=4,BC=AD=8,
∵点E是CD的中点,点Q是BC的中点,
∴BQ=CQ=4,CE=2,
∴AB=CQ,
∵PQ=2,
∴BP=2,
∴BP=CE,
又∵∠B=∠C=90°,
∴△ABP≌△QCE(SAS),
∴AP=QE;
(2)如图②,在AD上截取线段AF=PQ=2,作F点关于BC的对称点G,连接EG与BC交于一点即为Q点,过A点作FQ的平行线交BC于一点,即为P点,过G点作BC的平行线交DC的延长线于H点.
∵GH=DF=6,EH=2+4=6,∠H=90°,
∴∠GEH=45°,
∴∠CEQ=45°,
设BP=x,则CQ=BC-BP-PQ=8-x-2=6-x,
在△CQE中,
∵∠QCE=90°,∠CEQ=45°,
∴CQ=EC,
∴6-x=2,
解得x=4,
∴BP=4;
(3)如图③,作点P关于AD的对称点F,作点Q关于CD的对称点H,连接FH,交AD于M,交CD于N,连接PM,QN,此时四边形PQNM的周长最小,连接FP交AD于T,
∴PT=FT=4,QC=BC-BP-PQ=8-3-2=3=CH,
∴PF=8,PH=8,
∴PF=PH,
又∵∠FPH=90°,
∴∠F=∠H=45°,
∵PF⊥AD,CD⊥QH,
∴∠F=∠TMF=45°,∠H=∠CNH=45°,
∴FT=TM=4,CN=CH=3,
∴四边形PQNM的面积=×PF×PH-×PF×TM-×QH×CN=×8×8-×8×4-×6×3=7.
【点拨】本题是四边形综合题,考查了矩形的性质,全等三角形的判定和性质,轴对称求最短距离,直角三角形的性质;通过构造平行四边形和轴对称找到点P和点Q位置是解题的关键。
A
M
N
B
A
M
N
B
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学八年级上暑假预习课
第十六讲 最短路径
一、专题导航
二、知识点梳理
类型一、 垂直线段最短问题
方法技巧:一动点与一定点连成的线段中,若动点在定直线上,则垂线段最短。
典例剖析1
例1-1.如图,等腰三角形ABC底边BC的长为4 cm,面积为12 cm2,腰AB的垂直平分线EF交AB于点E,交AC于点F,若D为BC边上的中点,M为线段EF上一点,则△BDM的周长最小值为( )
A. 5 cm B. 6 cm C. 8 cm D. 10 cm
例1-2.如图,在△ABC中,AC=BC=8,∠ACB=120°,BD平分∠ABC交AC于点D,点E、F分别是线段BD,BC上的动点,则CE+EF的最小值是( )
A. 2 B. 4 C. 5 D. 6
例1-3.如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,∠ABC的平分线交AC于点D,点E,F分别是BD、AB上的动点,则AE+EF的最小值为( )
A. 2 B. 2.4 C. 2.5 D. 3
类型二、两点之间线段最短问题
定点关于定直线对称转化为两点之间线段最短求最值.
①两定一动
②一定两动
③两定两动
典例剖析2
例2-1.如图,∠MON=40°,P为∠MON内一点,A为OM上一点,B为ON上一点,当△PAB的周长取最小值时,∠APB的度数为( )
A. 40° B. 80° C. 100° D. 140°
例2-2.如图,在正方形中,,分别为,的中点,为对角线上的一个动点,则下列线段的长等于最小值的是( )
A. B.
C. D.
例2-3.如图,在△ABC中,点P在边BC上方,连接PB,PC,S△PBC=S△ABC=,当PB+PC取得最小值时,∠PBC的度数是( )
A. 30° B. 45° C. 60° D. 90°
例2-4.如图,A,B两个村庄独自从河流l上安装了两条灌溉管道AD,BE,AD⊥l于点D,BE⊥l于点E.某水务局准备为两村庄在河流l上重新安装一台大型的抽水设备灌溉农田.通过测量,确定在河流l的点P处安装抽水设备,则到两个村庄铺设的管道AP+BP的长度最短,此时测得∠PBE=30°,DE=150米,则AP+BP的最小值为( )
A. 180米 B. 210米 C. 240米 D. 300米
类型三、造桥选址问题
造桥选址问题
方法技巧:将分散的线段平移集中,再求最值.
典例剖析3
例3-1.如图,∠AOB=90°,OC=2,D为OC中点,长为1的线段EF(点F在点E的下方)在直线OB上移动,连接DE,CF,则DE+CF的最小值为( )
A. B.
C. 2 D. 3
例3-2.A和B两地在一条河的两岸,现要在河上造一座桥MN,使从A到B的路径AMNB最短的是(假定河的两岸是平行线,桥与河岸垂直)( )
A.
(BM垂直于a) B.
(AM不平行BN)
C.
(AN垂直于b) D. (AM平行BN)
例3-3.如图,△ABC中,∠ACB=90°,∠A=30°,BC=2,若D,E是边AB上的两个动点,F是边AC上的一个动点,DE=,则CD+EF的最小值为( )
A. - B. 3-
C. 1+ D. 3
变式训练
变式1、 垂直线段最短问题
1.如图,等边△ABC,边长为8,点D为边BC上一点,以AD为边在AD右侧作等边△ADE,连接CE,当△ADE周长最小时,CE的长度为( )
A. 1 B. 2 C. 4 D. 8
2.如图,在△AOB中,∠OAB=∠AOB=15°,OB=6,OC平分∠AOB,点P在射线OC上,点Q为边OA上一动点,则PA+PQ的最小值是( )
A. 1 B. 2 C. 3 D. 4
3.如图,在△ABC中,AB=BC,AC=2cm,,边BC的垂直平分线为l,点D是边AC的中点,点P是l上的动点,则△PCD的周长的最小值是______.
变式2、两点之间线段最短问题
1.现需要在某条街道l上修建一个核酸检测点P,向居住在A,B小区的居民提供核酸检测服务,要使P到A,B的距离之和最短,则核酸检测点P符合题意的是( )
A. B.
C. D.
2.如图,等边△ABC中,BD⊥AC于D,AD=3.5cm,点P、Q分别为AB、AD上的两个定点且BP=AQ=2cm,在BD上有一动点E使PE+QE最短,则PE+QE的最小值为( )
A. 3cm B. 4cm C. 5cm D. 6cm
3.如图,在锐角△ABC中,∠ACB=50°;边AB上有一定点P,M、N分别是AC和BC边上的动点,当△PMN的周长最小时,∠MPN的度数是( )
A. 50° B. 60° C. 70° D. 80°
4.如图,在平面直角坐标系xOy中,点A的坐标为(0,6),点B为x轴上一动点,以AB为边在直线AB的右侧作等边三角形ABC.若点P为OA的中点,连接PC,则PC的长的最小值为_____.
变式3、类型三、造桥选址问题
1.如图,矩形ABCD中,AB=4,BC=2,G是AD的中点,线段EF在边AB上左右滑动,若EF=1,则GE+CF的最小值为 _____.
2.如图所示,矩形ABCD中,AB=8,AD=4,点E是AD的中点,点F是AB上任意一点,沿着EF翻折,点A落在点G处,点H是CD上任意一点,连接HG和HB,则HG+HB的最小值为 _____.
3.如图,∠MON=15°,四边形ABCD的顶点A在∠MON的内部,B,C两点在OM上(C在B,O之间),且BC=1,点D在ON上,若当CD⊥OM时,四边形ABCD的周长最小,则此时AD的长度是_____.
能力提升
提升1、 垂直线段最短问题
1.如图,BD是△ABC的角平分线,E和F分别是AB和BD上的动点,已知△ABC的面积是12cm2,BC的长是8cm,则AF+EF的最小值是 _____cm.
2.如图,锐角△ABC中,BD是∠ABC的角平分线,M、N分别是BD、BC线段上运动的点,S△ABC=8,AB=4,则MN+MC的最小值是=_____.
3.如图,在Rt△ABC中,AB=6,∠BAC=30°,∠BAC的平分线交BC于点D,E,F分别是线段AD和AB上的动点,则BE+EF的最小值是_____.
提升2、两点之间线段最短问题
1.如图,等边△ABC中,BD⊥AC于D,QD=1.5,点P、Q分别为AB、AD上的两个定点且BP=AQ=2,在BD上有一动点E使PE+QE最短,则PE+QE的最小值为 _____.
2.如图,在△ABC中,AB=3,AC=4,BC=5,EF是BC的垂直平分线,P是直线EF上的任意一点,则PA+PB的最小值是 _____.
3.如图,A,B两个工厂位于一段直线形河的异侧,A厂距离河边AC=5km,B厂距离河边BD=1km,经测量CD=8km,现准备在河边某处(河宽不计)修一个污水处理厂E.
(1)设ED=x,请用x的代数式表示AE+BE的长;
(2)为了使两厂的排污管道最短,污水厂E的位置应怎样来确定此时需要管道多长?
(3)通过以上的解答,充分展开联想,运用数形结合思想,请你猜想的最小值为多少?
4.(1)小河的同旁有甲、乙两个村庄如图(1),现计划在河岸AB上建一个水泵站,向两村供水,用以解决村民生活用水问题.(保留作图痕迹)
①如果要求水泵站到甲、乙两村庄的距离相等,水泵站M应建在河岸AB上的何处?
②如果要求建造水泵站,供水管道使用建材最省,水泵站N又应建在河岸AB上的何处?
(2)如图(2),作出△ABC关于直线l的对称图形.
提升3、类型三、造桥选址问题
1.如图,A、B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A、B两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点.(保留作图痕迹)
2.如图,平行河岸两侧各有一城镇,,根据发展规划,要修建一条桥梁连接,两镇,已知相同长度造桥总价远大于陆上公路造价,为了尽量减少总造价,应该选择方案( )
A. B.
C. D.
3.在长方形ABCD中,AB=4,BC=8,点P、Q为BC边上的两个动点(点P位于点Q的左侧,P、Q均不与顶点重合),PQ=2
(1)如图①,若点E为CD边上的中点,当Q移动到BC边上的中点时,求证:AP=QE;
(2)如图②,若点E为CD边上的中点,在PQ的移动过程中,若四边形APQE的周长最小时,求BP的长;
(3)如图③,若M、N分别为AD边和CD边上的两个动点(M、N均不与顶点重合),当BP=3,且四边形PQNM的周长最小时,求此时四边形PQNM的面积.
人教版数学八年级上暑假预习课
第十六讲 最短路径(解析版)
一、专题导航
二、知识点梳理
类型一、 垂直线段最短问题
方法技巧:一动点与一定点连成的线段中,若动点在定直线上,则垂线段最短。
典例剖析1
例1-1.如图,等腰三角形ABC底边BC的长为4 cm,面积为12 cm2,腰AB的垂直平分线EF交AB于点E,交AC于点F,若D为BC边上的中点,M为线段EF上一点,则△BDM的周长最小值为( )
A. 5 cm B. 6 cm C. 8 cm D. 10 cm
【答案】C
【解析】连接AD,由于△ABC是等腰三角形,点D是BC边的中点,故AD⊥BC,再根据三角形的面积公式求出AD的长,再根据EF是线段AB的垂直平分线可知,点B关于直线EF的对称点为点A,故AD的长为BM+MD的最小值,由此即可得出结论.
如图,连接AD.
∵△ABC是等腰三角形,点D是BC边的中点,∴AD⊥BC,∴S△ABC=BC AD=×4×AD=12,解得:AD=6(cm).
∵EF是线段AB的垂直平分线,∴点B关于直线EF的对称点为点A,∴AD的长为BM+MD的最小值,∴△BDM的周长最短=(BM+MD)+BD=AD+BC=6+×4=6+2=8(cm).
故选C.
【点睛】本题考查的是轴对称﹣最短路线问题,熟知等腰三角形三线合一的性质是解答此题的关键.
例1-2.如图,在△ABC中,AC=BC=8,∠ACB=120°,BD平分∠ABC交AC于点D,点E、F分别是线段BD,BC上的动点,则CE+EF的最小值是( )
A. 2 B. 4 C. 5 D. 6
【答案】B
【解析】作C点关于BD的对称点C',过C'作C'F⊥BC交BD于点E,交BC于点F,CE+EF的最小值C'F的长.
解:作C点关于BD的对称点C',过C'作C'F⊥BC交BD于点E,交BC于点F,
∴CE+EF=C'E+EF≥C'F,
∴CE+EF的最小值C'F的长,
∴CC'⊥BD,
∵BD平分∠ABC,
∴∠C'BG=∠GBC,
在△C'BG和△CBG中,
,
∴△C'BG≌△CBG(ASA),
∴BC=BC',
∵AC=BC=8,∠ACB=120°,
∴∠ABC=30°,BC'=8,
在Rt△BFC'中,C'F=BC' sin30°=8×=4,
∴CE+EF的最小值为4,
故选:B.
例1-3.如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,∠ABC的平分线交AC于点D,点E,F分别是BD、AB上的动点,则AE+EF的最小值为( )
A. 2 B. 2.4 C. 2.5 D. 3
【答案】B
【解析】作点A关于BD的对称点M,过M作MF⊥AB于F,交BD于E,则AE+EF的最小值是MF的长.由MF∥CA可得,进而可得答案.
解:作点A关于BD的对称点M,
∵BD平分∠ABC,
∴M落在BC上.
∴BM=BA=4,
过M作MF⊥AB于F,交BD于E,
则AE+EF的最小值是MF的长.
∵∠MFB=∠CAB=90°,
∴MF∥CA,
∴,
即,MF=2.4,
∴AE+EF=MF=2.4.
故选:B.
类型二、两点之间线段最短问题
定点关于定直线对称转化为两点之间线段最短求最值.
①两定一动
②一定两动
③两定两动
典例剖析2
例2-1.如图,∠MON=40°,P为∠MON内一点,A为OM上一点,B为ON上一点,当△PAB的周长取最小值时,∠APB的度数为( )
A. 40° B. 80° C. 100° D. 140°
【答案】C
【解析】如图,作P点关于OM、ON的对称点P1,P2,PP1与OM交点为C,PP2与ON交点为D,连接P1P2交OM、ON于A、B两点,则∠P1PA=∠P1,∠P2PB=∠P2,由题意知,当P1,A,B,P2四点共线时,△PAB的周长最小,由PP1⊥OM,PP2⊥ON,可知∠PCO=∠PDO=90°,∠P1PP2=360°-∠PCO-∠PDO-∠MON=140°,则∠P1PA+∠P2PB=∠P1+∠P2=180°-∠P1PP2=40°,根据∠APB=∠P1PP2-(∠P1PA+∠P2PB),计算求解即可.
解:如图,作P点关于OM、ON的对称点P1,P2,PP1与OM交点为C,PP2与ON交点为D,连接P1P2交OM、ON于A、B两点,则∠P1PA=∠P1,∠P2PB=∠P2,
由题意知,当P1,A,B,P2四点共线时,△PAB的周长最小,
∵PP1⊥OM,PP2⊥ON,
∴∠PCO=∠PDO=90°,
∴∠P1PP2=360°-∠PCO-∠PDO-∠MON=140°,
∴∠P1PA+∠P2PB=∠P1+∠P2=180°-∠P1PP2=40°,
∴∠APB=∠P1PP2-(∠P1PA+∠P2PB)=100°,
故选:C.
例2-2.如图,在正方形中,,分别为,的中点,为对角线上的一个动点,则下列线段的长等于最小值的是( )
A. B.
C. D.
【答案】D
【解析】连接,当点,,在同一直线上时,的最小值为长,依据,即可得到最小值等于线段的长.
解:如图,连接,
由,,,
可得,
,
,
当点,,在同一直线上时,
的最小值为长,
此时,由,,,
可得,
,
最小值等于线段的长,
故选:D.
【点睛】本题考查的是轴对称,最短路线问题,解题的关键是根据题意作出关于的对称点.
例2-3.如图,在△ABC中,点P在边BC上方,连接PB,PC,S△PBC=S△ABC=,当PB+PC取得最小值时,∠PBC的度数是( )
A. 30° B. 45° C. 60° D. 90°
【答案】B
【解析】由三角形面积关系得出AP与BC平行,AP与BC的距离为BC,作点B关于直线AP的对称点B',连接B'C交AP于P′,则BB'⊥AP,P′B=P′B',此时点P′到B、C两点距离之和最小,证明△BB'C是等腰直角三角形,即可得出答案.
解:如图,连接AP,
∵S△PBC=S△ABC==BC BC,
∴AP∥BC平行,AP与BC的距离为BC,
作B点关于AP的对称点B',连接B'C,交AP于P′点,连接P'B,
由对称性可知,B'P′=BP′,
∴PB+PC=B'P′+P′C=B'C,此时PB+PC最小,
∵BB'=BC,
∴△BCB'是等腰直角三角形,
∴∠B'CB=∠B'=45°,
∴∠B'BP′=45°,
∴∠P′BC=45°,
∴当PB+PC取得最小值时,∠PBC的度数是45°.
故选:B.
例2-4.如图,A,B两个村庄独自从河流l上安装了两条灌溉管道AD,BE,AD⊥l于点D,BE⊥l于点E.某水务局准备为两村庄在河流l上重新安装一台大型的抽水设备灌溉农田.通过测量,确定在河流l的点P处安装抽水设备,则到两个村庄铺设的管道AP+BP的长度最短,此时测得∠PBE=30°,DE=150米,则AP+BP的最小值为( )
A. 180米 B. 210米 C. 240米 D. 300米
【答案】D
【解析】延长AD到点F,使FD=AD,连接FP,则点F与点A关于直线l对称,所以FP=AP,则AP+BP=FP+BP,则AP+BP最短,可知FP+BP最短,则F、P、B三点在同一直线上,所以∠A=∠F=∠PBE=30°,则AP=2PD,BP=2PE,AP+BP=2DE=300米,于是得到问题的答案.
解:延长AD到点F,使FD=AD,连接FP,
∵AD⊥l,
∴点F与点A关于直线l对称,
∴FP=AP,
∴AP+BP=FP+BP,
∵AP+BP最短,
∴FP+BP最短,
∴F、P、B三点在同一直线上,
∵BE⊥l,
∴AD∥BE,∠ADP=∠BEP=90°,
∴∠A=∠F=∠PBE=30°,
∴AP=2PD,BP=2PE,
∴AP+BP=2(PD+PE)=2DE=2×150=300(米),
∴AP+BP的最小值为300米,
故选:D.
类型三、造桥选址问题
造桥选址问题
方法技巧:将分散的线段平移集中,再求最值.
典例剖析3
例3-1.如图,∠AOB=90°,OC=2,D为OC中点,长为1的线段EF(点F在点E的下方)在直线OB上移动,连接DE,CF,则DE+CF的最小值为( )
A. B.
C. 2 D. 3
【答案】B
【解析】如图,作点D关于OB的对称点T,作TR∥OB,使得TR=EF,连接CR交OB于F,在FO的延长线上,取点E,使得EF=1,连接ET.DE,此时DE+CF的值最小.
解:如图,作点D关于OB的对称点T,作TR∥OB,使得TR=EF,连接CR交OB于F,在FO的延长线上,取点E,使得EF=1,连接ET.DE,此时DE+CF的值最小.
∵RT=EF=1,RT∥EF,
∴四边形TRFE是平行四边形,
∴ET=FR,
∵D,T关于OB对称,
∴ED=ET,
∴DE=RF,
∴DE+CF=RF+FC=RC,此时CR的值最小,最小值===,
故选:B.
例3-2.A和B两地在一条河的两岸,现要在河上造一座桥MN,使从A到B的路径AMNB最短的是(假定河的两岸是平行线,桥与河岸垂直)( )
A.
(BM垂直于a) B.
(AM不平行BN)
C.
(AN垂直于b) D. (AM平行BN)
【答案】D
【解析】过A作河的垂线AH,要使最短,MN⊥直线a,AI=MN,连接BI即可得出N,作出AM、MN、BN即可.
解:根据垂线段最短,得出MN是河的宽时,MN最短,即MN⊥直线a(或直线b),只要AM+BN最短即可,
即过A作河岸a的垂线AH,垂足为H,在直线AH上取点I,使AI等于河宽.
连接IB交河的b边岸于N,作MN垂直于河岸交a边的岸于M点,所得MN即为所求.
故选:D.
例3-3.如图,△ABC中,∠ACB=90°,∠A=30°,BC=2,若D,E是边AB上的两个动点,F是边AC上的一个动点,DE=,则CD+EF的最小值为( )
A. - B. 3-
C. 1+ D. 3
【答案】B
【解析】首先△ABC是含有30°角的直角三角形,因此可以得知各边的长分别为AB=4,AC=2.因为D,E是边AB上的两个动点,F是边AC上的一个动点,求CD+EF的最小值,就是需要转换成同一直线上求解,即求C关于AB的对称点C1,作C1C2∥AB.构建平行四边形C1DEC2,作C2F⊥AC于F,交AB于E.利用平行四边形和对称图形的性质,找出线段之间的关系.
解:如图,过C作AB的对称点C1,连接CC1,交AB于N;过C1作C1C2∥AB,且C1C2=,过C2作C2F⊥AC于F,交AB于E,C2F的长度即为所求最小值,
∵CC2∥DE,CC2=DE,
∴四边形C1DEC2是平行四边形,
∴C1D=C2E,
又∵C、C1关于AB对称,
∴CD=C1D,
∴CD+EF=C2F,
∵∠A=30°,∠ACB=90°,
∴AC=BC=2,
∴CN=,AN=3,
过C2作C2M⊥AB,则C2M=C1N=CN=,
∴C2M∥C1N,C1C2∥MN,
∴MN=C1C2=,
∵∠MEC2=∠AEF,∠AFE=∠C2ME=90°,
∴∠MC2E=∠A=30°,
在Rt△C2ME中,ME=1,C2M=,C2E=2,
∴AE=AN-MN-ME=3--1=2-,
∴EF=1-,
∴C2F=2+1-=3-.
故选:B.
变式训练
变式1、 垂直线段最短问题
1.如图,等边△ABC,边长为8,点D为边BC上一点,以AD为边在AD右侧作等边△ADE,连接CE,当△ADE周长最小时,CE的长度为( )
A. 1 B. 2 C. 4 D. 8
【答案】C
【解析】由等边三角形的性质得C△ADE=3AD,当△ADE周长最小时,AD⊥BC时,AD最小,利用全等三角形的判定边角边得△ABD和△ACE全等,即得CE的长度.
解:
∵△ADE是等边三角形,
∴AD=DE=AE,
∴C△ADE=3AD,
当△ADE周长最小时,
即AD最小,
当AD⊥BC时,AD最小,
此时,BD=AB sin30°=4,
∵△ABC是等边三角形,
∴∠1+∠2=60°,
又∵∠2+∠3=60°,
∴∠1=∠3,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE=4,
故选:C.
2.如图,在△AOB中,∠OAB=∠AOB=15°,OB=6,OC平分∠AOB,点P在射线OC上,点Q为边OA上一动点,则PA+PQ的最小值是( )
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】作AH⊥OB于H.交OC于P,作PQ⊥OA于Q,可得PA+PQ=PA+PH=AH,根据垂线段最短,PA+PQ最小值为AH,
解:作AH⊥OB于H,交OC于P,作PQ⊥OA于Q,
∵∠OAB=∠AOB=15°,
∴PH=PQ,
∴PA+PQ=PA+PH=AH,
∴PA+PQ的最小值为AH,
在Rt△ABH中,∵OB=AB=6,∠ABH=30°,
∴AH=AB=3,
∴PA+PQ的最小值为3,
故选:C.
3.如图,在△ABC中,AB=BC,AC=2cm,,边BC的垂直平分线为l,点D是边AC的中点,点P是l上的动点,则△PCD的周长的最小值是______.
【答案】4
【解析】连接BD,由于AB=BC,点D是AC边的中点,故BD⊥AC,再根据三角形的面积公式求出BD的长,再根据直线l是线段BC的垂直平分线可知,点C关于直线l的对称点为点B,故BD的长为CP+PD的最小值,由此即可得出结论.
解:连接BD,
∵AB=BC,点D是BC边的中点,
∴BD⊥AC,
∴S△ABC=AC BD=×2×BD=3,
解得BD=3,
∵直线l是线段BC的垂直平分线,
∴点C关于直线l的对称点为点B,
∴AB的长为CP+PD的最小值,
∴△CDP的周长最短=(CP+PD)+CD=BD+AC=3+1=4.
故答案为:4.
【点睛】本题考查的是轴对称-最短路线问题,熟知等腰三角形三线合一的性质是解答此题的关键.
变式2、两点之间线段最短问题
1.现需要在某条街道l上修建一个核酸检测点P,向居住在A,B小区的居民提供核酸检测服务,要使P到A,B的距离之和最短,则核酸检测点P符合题意的是( )
A. B.
C. D.
【答案】A
【解析】作A点关于直线l的对称点,连接对称点和点B交l于点P,进而根据轴对称性质解答即可.
解:作A点关于直线l的对称点,连接对称点和点B交l于点P,P即为所求.
故选:A.
2.如图,等边△ABC中,BD⊥AC于D,AD=3.5cm,点P、Q分别为AB、AD上的两个定点且BP=AQ=2cm,在BD上有一动点E使PE+QE最短,则PE+QE的最小值为( )
A. 3cm B. 4cm C. 5cm D. 6cm
【答案】C
【解析】作点Q关于BD的对称点Q′,连接PQ′交BD于E,连接QE,此时PE+EQ的值最小.最小值PE+EQ=PE+EQ′=PQ′.
解:如图,∵△ABC是等边三角形,
∴BA=BC,
∵BD⊥AC,
∴AD=DC=3.5cm,
作点Q关于BD的对称点Q′,连接PQ′交BD于E,连接QE,此时PE+EQ的值最小.最小值PE+EQ=PE+EQ′=PQ′,
∵AQ=2cm,AD=DC=3.5cm,
∴QD=DQ′=1.5(cm),
∴CQ′=BP=2(cm),
∴AP=AQ′=5(cm),
∵∠A=60°,
∴△APQ′是等边三角形,
∴PQ′=PA=5(cm),
∴PE+QE的最小值为5cm.
故选:C.
3.如图,在锐角△ABC中,∠ACB=50°;边AB上有一定点P,M、N分别是AC和BC边上的动点,当△PMN的周长最小时,∠MPN的度数是( )
A. 50° B. 60° C. 70° D. 80°
【答案】D
【解析】根据对称的性质,易求得∠C+∠EPF=180°,由∠ACB=50°,易求得∠D+∠G=50°,继而求得答案.
解:作点P关于AC,BC的对称点D,G,连接PD,PG分别交AC,BC于E,F,连接DG交AC于M,交BC于N,连接PM,PN.此时△PMN的周长最小.
∵PD⊥AC,PG⊥BC,
∴∠PEC=∠PFC=90°,
∴∠C+∠EPF=180°,
∵∠C=50°,
∴∠EPF=130°,
∵∠D+∠G+∠EPF=180°,
∴∠D+∠G=50°,
由对称可知:∠G=∠GPN,∠D=∠DPM,
∴∠GPN+∠DPM=50°,
∴∠MPN=130°-50°=80°,
故选:D.
4.如图,在平面直角坐标系xOy中,点A的坐标为(0,6),点B为x轴上一动点,以AB为边在直线AB的右侧作等边三角形ABC.若点P为OA的中点,连接PC,则PC的长的最小值为_____.
【答案】
【解析】以AP为边作等边三角形APE,连接BE,过点E作EF⊥AP于F,由“SAS”可证△ABE≌△ACP,可得BE=PC,则当BE有最小值时,PC有最小值,即可求解.
解:如图,以AP为边作等边三角形APE,连接BE,过点E作EF⊥AP于F,
∵点A的坐标为(0,6),
∴OA=6,
∵点P为OA的中点,
∴AP=3,
∵△AEP是等边三角形,EF⊥AP,
∴AF=PF=,AE=AP,∠EAP=∠BAC=60°,
∴∠BAE=∠CAP,
在△ABE和△ACP中,
∴△ABE≌△ACP(SAS),
∴BE=PC,
∴当BE有最小值时,PC有最小值,
即BE⊥x轴时,BE有最小值,
∴BE的最小值为OF=OP+PF=3+=,
∴PC的最小值为,
故答案为.
【点睛】本题考查了轴对称 最短路线问题,全等三角形的判定和性质,等边三角形的判定和性质,添加恰当辅助线构造全等三角形是本题的关键.
变式3、类型三、造桥选址问题
1.如图,矩形ABCD中,AB=4,BC=2,G是AD的中点,线段EF在边AB上左右滑动,若EF=1,则GE+CF的最小值为 _____.
【答案】3
【解析】解法一:利用已知可以得出GC,EF长度不变,求出GE+CF最小时即可得出四边形CGEF周长的最小值,利用轴对称得出E,F位置,即可求出.
解法二:设AE=x,则BF=3-x,根据勾股定理可得:EG+CF=+,由勾股定理构建另一矩形EFGH,根据线段的性质:两点之间线段最短可得结论.
解:解法一:如图,作G关于AB的对称点G',在CD上截取CH=1,然后连接HG'交AB于E,在EB上截取EF=1,此时GE+CF的值最小,
∵CH=EF=1,CH∥EF,
∴四边形EFCH是平行四边形,
∴EH=CF,
∴G'H=EG'+EH=EG+CF,
∵AB=4,BC=AD=2,G为边AD的中点,
∴DG'=AD+AG'=2+1=3,DH=4-1=3,
由勾股定理得:HG'==3,
即GE+CF的最小值为3.
解法二:∵AG=AD=1,
设AE=x,则BF=AB-EF-AE=4-x-1=3-x,
由勾股定理得:EG+CF=+,
如图,矩形EFGH中,EH=3,GH=2,GQ=1,
P为FG上一动点,设PG=x,则FP=3-x,
∴EP+PQ=+,
当E,P,Q三点共线时,EP+PQ最小,最小值是3,
即EG+CF的最小值是3.
故答案为:3.
2.如图所示,矩形ABCD中,AB=8,AD=4,点E是AD的中点,点F是AB上任意一点,沿着EF翻折,点A落在点G处,点H是CD上任意一点,连接HG和HB,则HG+HB的最小值为 _____.
【答案】8
【解析】作点B关于CD的对称点B',连接B'G,交CD于点H.则HB=HB',则HG+HB=HG+HB',其最小值为B'G的长,点G在以点E为圆心,2为半径的圆周上运动,所以EG+GB'的最小值为EB',因此B'G的最小值为:B'E-2.
解:作点B关于CD的对称点B',连接B'G,交CD于点H.
则HB=HB',
则HG+HB=HG+HB',其最小值为B'G的长.
∵AD=4,点E是AD的中点,
∴AE=DE=GE=2,
∴点G在以点E为圆心,2为半径的圆周上运动,
∵EG+GB'≥EB',
∴EG+GB'的最小值为EB',
∵EG=2,
∴B'G的最小值为:B'E-2.
在RtΔB'ME中,
EM=2+4=6,B'M=8,
B'E==10.
∴B'G的最小值为:B'E-2=10-2=8.
即HG+HB最小值为8.
故答案为:8.
3.如图,∠MON=15°,四边形ABCD的顶点A在∠MON的内部,B,C两点在OM上(C在B,O之间),且BC=1,点D在ON上,若当CD⊥OM时,四边形ABCD的周长最小,则此时AD的长度是_____.
【答案】2
【解析】根据最短问题解决的方法,分别作A关于OM,ON的对称点,提供连接对称点,列出四边形周长公式,根据已知条件,要使得四边形ABCD的周长最短,只需要四点共线,然后解直角三角形求出AD即可.
解:如图1中,分别作点A关于直线OM,ON的对称点A1,A2,连接BA1,DA2,过点A1作A1A3⊥CD于A3,
由图可知:AQ=A1Q=A3C,AB>AQ,当A,B,A1共线时,AB最短,此时A3C=AB,
∵四边形ABCD的周长=AB+BC+CD+AD=A3C+CD+DA2+BC=A3C+CD+DA2+1,
∴当A3,C,D,A2共线时,四边形ABCD的周长最短(如图2中),作AH⊥CD于H.
∵∠MON=15°,CD⊥OM,
∴∠ODC=90°-15°=75°,
∴∠FDA2=∠ODC=∠ADF=75°,
∴∠ADH=180°-75°-75°=30°,
在Rt△ADH中,AD===2.
故答案为2.
能力提升
提升1、 垂直线段最短问题
1.如图,BD是△ABC的角平分线,E和F分别是AB和BD上的动点,已知△ABC的面积是12cm2,BC的长是8cm,则AF+EF的最小值是 _____cm.
【答案】3
【解析】作E关于BD的对称点G,连接FG,过点A作AH⊥BC于H,将AF+EF转化AF+FG,由点到直线垂线段最短的AF+FG最小值为AH的长,由△ABC的面积是12cm2,BC的长是8cm,求出AH即可.
解:作E关于BD的对称点G,连接FG,过点A作AH⊥BC于H,
∵BD是△ABC的角平分线,
∴G必在BC上,
∵E、G关于BD对称,
∴EF=FG,
∴AF+EF=AF+FG,
∵点F在垂线段AH上最短,
∴AF+FG最小值为AH的长,
∵△ABC的面积是12cm2,BC的长是8cm,
∴×BC AH=12,
∴AH=3cm,
∴AF+EF的最小值是3cm,
故答案为:3.
2.如图,锐角△ABC中,BD是∠ABC的角平分线,M、N分别是BD、BC线段上运动的点,S△ABC=8,AB=4,则MN+MC的最小值是=_____.
【答案】4
【解析】作N点关于BD的对称点N',连接CN',过C作CE⊥AB交于点E,则N'必在AB上,NM+CM=MN'+CN=CN'≥CE,由S△ABC=8,AB=4,可求EC=4,即MN+MC的最小值是4.
解:作N点关于BD的对称点N',连接CN',过C作CE⊥AB交于点E,
∵BD是∠ABC的角平分线,
∴N'必在AB上,
∴NM+CM=MN'+CN=CN'≥CE,
∴当CN'=CE时,MN+MC的值最小,
∵S△ABC=8,AB=4,
∴EC=4,
∴MN+MC的最小值是4,
故答案为4.
3.如图,在Rt△ABC中,AB=6,∠BAC=30°,∠BAC的平分线交BC于点D,E,F分别是线段AD和AB上的动点,则BE+EF的最小值是_____.
【答案】3
【解析】作BH⊥AC交AD于点E,作EF⊥AB于F,根据角平分线的性质可得EH=EF,即可求得BE+EF=BH,根据H是与B点的距离最短的点,即为BH最短即可解题.
解:作BH⊥AC交AD于点E,作EF⊥AB于F,
∵AD平分∠BAC,EH⊥AC,EF⊥AB,
∴EF=EH,
∴BE+EF=BE+EH=BH,
∵H是与B点的距离最短的点,即为BH最短,
∴BE+EF最短为BH,
∵AB=6,∠BAC=30°,
∴BH=AB=3,
故答案为 3.
提升2、两点之间线段最短问题
1.如图,等边△ABC中,BD⊥AC于D,QD=1.5,点P、Q分别为AB、AD上的两个定点且BP=AQ=2,在BD上有一动点E使PE+QE最短,则PE+QE的最小值为 _____.
【答案】5
【解析】作点Q关于BD的对称点Q′,连接PQ′交BD于E,连接QE,此时PE+EQ的值最小.最小值PE+PQ=PE+EQ′=PQ′.
解:如图,∵△ABC是等边三角形,
∴BA=BC,
∵BD⊥AC,AQ=2,QD=1.5,
∴AD=DC=AQ+QD=3.5,
作点Q关于BD的对称点Q′,连接PQ′交BD于E,连接QE,此时PE+EQ的值最小.最小值PE+QE=PE+EQ′=PQ′,
∵AQ=2,AD=DC=3.5,
∴QD=DQ′=1.5,
∴CQ′=BP=2,
∴AP=AQ′=5,
∵∠A=60°,
∴△APQ′是等边三角形,
∴PQ′=PA=5,
∴PE+QE的最小值为5.
故答案为:5.
2.如图,在△ABC中,AB=3,AC=4,BC=5,EF是BC的垂直平分线,P是直线EF上的任意一点,则PA+PB的最小值是 _____.
【答案】4
【解析】根据线段的垂直平分线的性质可得BE=EC,根据两点之间线段最短即可求解.
解:如图,连接BP,
∵EF是BC的垂直平分线,
∴BP=CP,
根据两点之间线段最短,
∴PA+PB=PA+PC=AC,
∴PA+PB的最小值即为AC的长为4.
∴PA+PB的最小值为4.
故答案为:4.
3.如图,A,B两个工厂位于一段直线形河的异侧,A厂距离河边AC=5km,B厂距离河边BD=1km,经测量CD=8km,现准备在河边某处(河宽不计)修一个污水处理厂E.
(1)设ED=x,请用x的代数式表示AE+BE的长;
(2)为了使两厂的排污管道最短,污水厂E的位置应怎样来确定此时需要管道多长?
(3)通过以上的解答,充分展开联想,运用数形结合思想,请你猜想的最小值为多少?
【解析】(1)依据ED=x,AC⊥CD、BD⊥CD,故根据勾股定理可用x表示出AE+BE的长;
(2)根据两点之间线段最短可知连接AB与CD的交点就是污水处理厂E的位置.过点B作BF⊥AC于F,构造出直角三角形,利用勾股定理求出AB的长;
(3)根据AE+BE=可作出图形,当A、E、B共线时,利用勾股定理求出AB的值即可.
解:(1)在Rt△ACE和Rt△BDE中,根据勾股定理可得AE=,BE=,
∴AE+BE=+,
(2)根据两点之间线段最短可知,连接AB与CD的交点就是污水处理厂E的位置.
过点B作BF⊥AC于F,则有BF=CD=8,BD=CF=1.
∴AF=AC+CF=6.
在Rt△ABF中,BA=,
∴此时最少需要管道10km.
(3)根据以上推理,可作出下图,设ED=x,BD=3,CD=15,AC=5,当A、E、B共线时,求出AB的值即为原式的最小值.
在Rt△ABF中,AF=8,BF=CD=15,
由勾股定理可得:AB=,
∴的最小值为17.
4.(1)小河的同旁有甲、乙两个村庄如图(1),现计划在河岸AB上建一个水泵站,向两村供水,用以解决村民生活用水问题.(保留作图痕迹)
①如果要求水泵站到甲、乙两村庄的距离相等,水泵站M应建在河岸AB上的何处?
②如果要求建造水泵站,供水管道使用建材最省,水泵站N又应建在河岸AB上的何处?
(2)如图(2),作出△ABC关于直线l的对称图形.
【解析】(1)①利用线段的垂直平分线的性质解决问题即可.
②利用轴对称解决最短问题即可.
(2)分别作出A,B,C关于直线l的对称点A′,B′,C′即可.
解:(1)①如图(1)中,点E即为所求.
②如图(1)-1中,点E即为所求.
(2)如图(2)中,△A′B′C′即为所求.
提升3、类型三、造桥选址问题
1.如图,A、B是两个蓄水池,都在河流a的同侧,为了方便灌溉作物,要在河边建一个抽水站,将河水送到A、B两地,问该站建在河边什么地方,可使所修的渠道最短,试在图中确定该点.(保留作图痕迹)
【解析】根据两点间线段最短可知作点A关于直线a对称的点C,连接BC交a于点P,则点P就是抽水站的位置.
解:作点A关于直线a对称的点C,连接BC交a于点P,则点P就是抽水站的位置.
2.如图,平行河岸两侧各有一城镇,,根据发展规划,要修建一条桥梁连接,两镇,已知相同长度造桥总价远大于陆上公路造价,为了尽量减少总造价,应该选择方案( )
A. B.
C. D.
【答案】C
【分析】作PP'垂直于河岸L,使PP′等于河宽,连接QP′,与河岸L相交于N,作NM⊥L,根据平行线的判定与性质,易证得此时PM+NQ最短.
【详解】解:如图,作PP'垂直于河岸L,使PP′等于河宽,连接QP′,与河岸L相交于N,作NM⊥L,则MN∥PP′且MN=PP′,于是四边形PMNP′为平行四边形,故PM=NP′.根据“两点之间线段最短”,QP′最短,即PM+NQ最短.观察选项,选项C符合题意.
故选C.
【点睛】本题主要考查最短路径问题,解此题的关键在于熟练掌握其知识点.
3.在长方形ABCD中,AB=4,BC=8,点P、Q为BC边上的两个动点(点P位于点Q的左侧,P、Q均不与顶点重合),PQ=2
(1)如图①,若点E为CD边上的中点,当Q移动到BC边上的中点时,求证:AP=QE;
(2)如图②,若点E为CD边上的中点,在PQ的移动过程中,若四边形APQE的周长最小时,求BP的长;
(3)如图③,若M、N分别为AD边和CD边上的两个动点(M、N均不与顶点重合),当BP=3,且四边形PQNM的周长最小时,求此时四边形PQNM的面积.
【答案】(1)见解析; (2) 4; (3) 4
【分析】(1)由“SAS”可证△ABP≌△QCE,可得AP=QE;
(2)要使四边形APQE的周长最小,由于AE与PQ都是定值,只需AP+EQ的值最小即可.为此,先在BC边上确定点P、Q的位置,可在AD上截取线段AF=DE=2,作F点关于BC的对称点G,连接EG与BC交于一点即为Q点,过A点作FQ的平行线交BC于一点,即为P点,则此时AP+EQ=EG最小,然后过G点作BC的平行线交DC的延长线于H点,那么先证明∠GEH=45°,再由CQ=EC即可求出BP的长度;
(3)要使四边形PQNM的周长最小,由于PQ是定值,只需PM+MN+QN的值最小即可,作点P关于AD的对称点F,作点Q关于CD的对称点H,连接FH,交AD于M,交CD于N,连接PM,QN,此时四边形PQNM的周长最小,由面积和差关系可求解.
(1)解:证明:∵四边形ABCD是矩形,
∴CD=AB=4,BC=AD=8,
∵点E是CD的中点,点Q是BC的中点,
∴BQ=CQ=4,CE=2,
∴AB=CQ,
∵PQ=2,
∴BP=2,
∴BP=CE,
又∵∠B=∠C=90°,
∴△ABP≌△QCE(SAS),
∴AP=QE;
(2)如图②,在AD上截取线段AF=PQ=2,作F点关于BC的对称点G,连接EG与BC交于一点即为Q点,过A点作FQ的平行线交BC于一点,即为P点,过G点作BC的平行线交DC的延长线于H点.
∵GH=DF=6,EH=2+4=6,∠H=90°,
∴∠GEH=45°,
∴∠CEQ=45°,
设BP=x,则CQ=BC-BP-PQ=8-x-2=6-x,
在△CQE中,
∵∠QCE=90°,∠CEQ=45°,
∴CQ=EC,
∴6-x=2,
解得x=4,
∴BP=4;
(3)如图③,作点P关于AD的对称点F,作点Q关于CD的对称点H,连接FH,交AD于M,交CD于N,连接PM,QN,此时四边形PQNM的周长最小,连接FP交AD于T,
∴PT=FT=4,QC=BC-BP-PQ=8-3-2=3=CH,
∴PF=8,PH=8,
∴PF=PH,
又∵∠FPH=90°,
∴∠F=∠H=45°,
∵PF⊥AD,CD⊥QH,
∴∠F=∠TMF=45°,∠H=∠CNH=45°,
∴FT=TM=4,CN=CH=3,
∴四边形PQNM的面积=×PF×PH-×PF×TM-×QH×CN=×8×8-×8×4-×6×3=7.
【点拨】本题是四边形综合题,考查了矩形的性质,全等三角形的判定和性质,轴对称求最短距离,直角三角形的性质;通过构造平行四边形和轴对称找到点P和点Q位置是解题的关键。
A
M
N
B
A
M
N
B
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
