华师版七年级数学上《5.1相交线》同步测试(含答案)
文档属性
| 名称 | 华师版七年级数学上《5.1相交线》同步测试(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 126.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-03 22:58:42 | ||
图片预览

文档简介
5.1相交线同步测试
一、选择题(每题3分,满分24分)
1.如图,在所标识的角中,互为对顶角的两个角是( )
A.∠2和∠3 B.∠1和∠3 C.∠1和∠4 D.∠1和∠2
2.已知:如图,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是( )
A.相等 B.互余 C.互补 D.互为对顶角
3.如图,直线AB、CD相交于O点,∠AOD+∠BOC=236°,则∠AOC=( )
A.72° B.62° C.124° D.144°
4.如图,有三条公路,其中AC与AB垂直,小明和小亮分别沿AC,BC同时出发骑车到C城,若他们同时到达,则下列判断中正确的是( )
A.小亮骑车的速度快 B.小明骑车的速度快
C.两人一样快 D.因为不知道公路的长度,所以无法判断他们速度的快慢
5.如图,下列说法不正确的是( )
A.∠1和∠3是对顶角 B.∠1和∠4是内错角
C.∠3和∠4是同位角 D.∠1和∠2是同旁内角
6.如图,直线AB,CD相交于点O,OM⊥AB,若∠COB=135°,则∠MOD等于( )
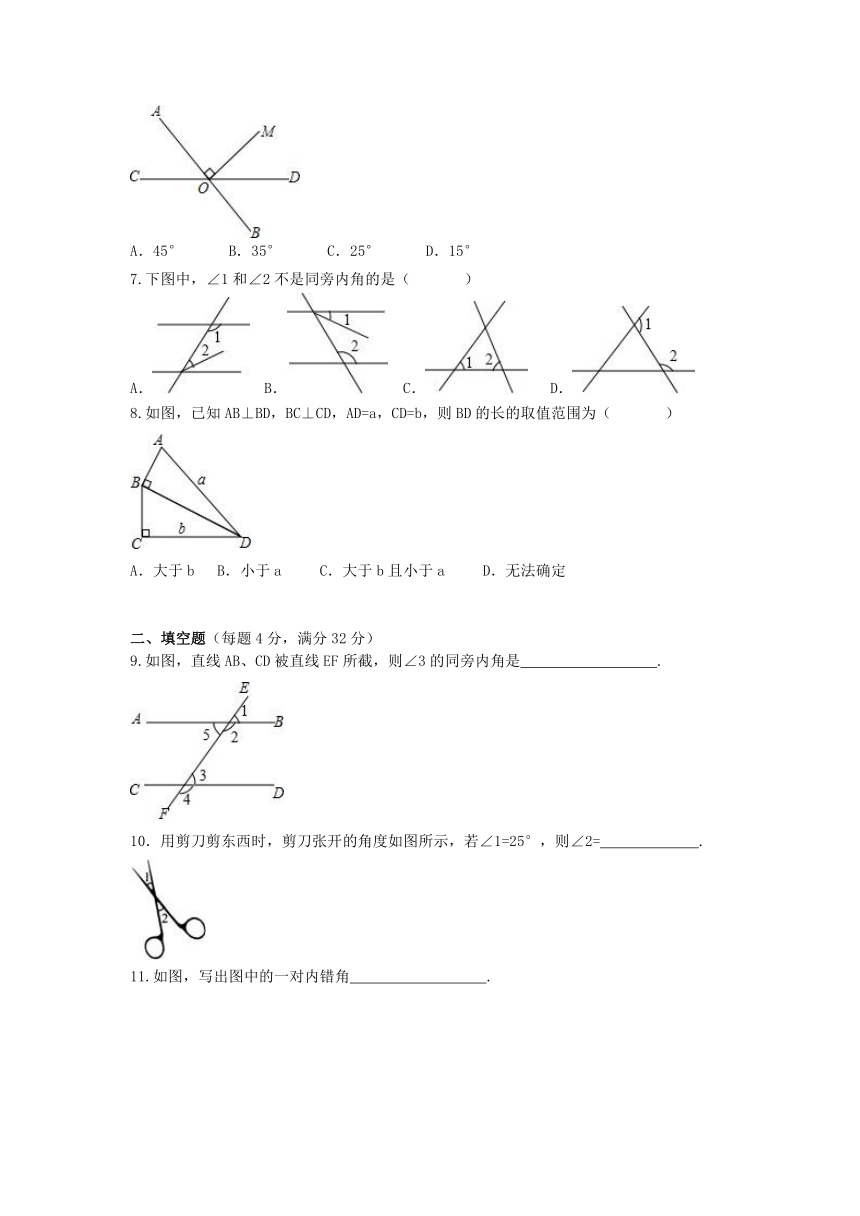
A.45° B.35° C.25° D.15°
7.下图中,∠1和∠2不是同旁内角的是( )
A. B. C. D.
8.如图,已知AB⊥BD,BC⊥CD,AD=a,CD=b,则BD的长的取值范围为( )
A.大于b B.小于a C.大于b且小于a D.无法确定
二、填空题(每题4分,满分32分)
9.如图,直线AB、CD被直线EF所截,则∠3的同旁内角是 .
10.用剪刀剪东西时,剪刀张开的角度如图所示,若∠1=25°,则∠2= .
11.如图,写出图中的一对内错角 .
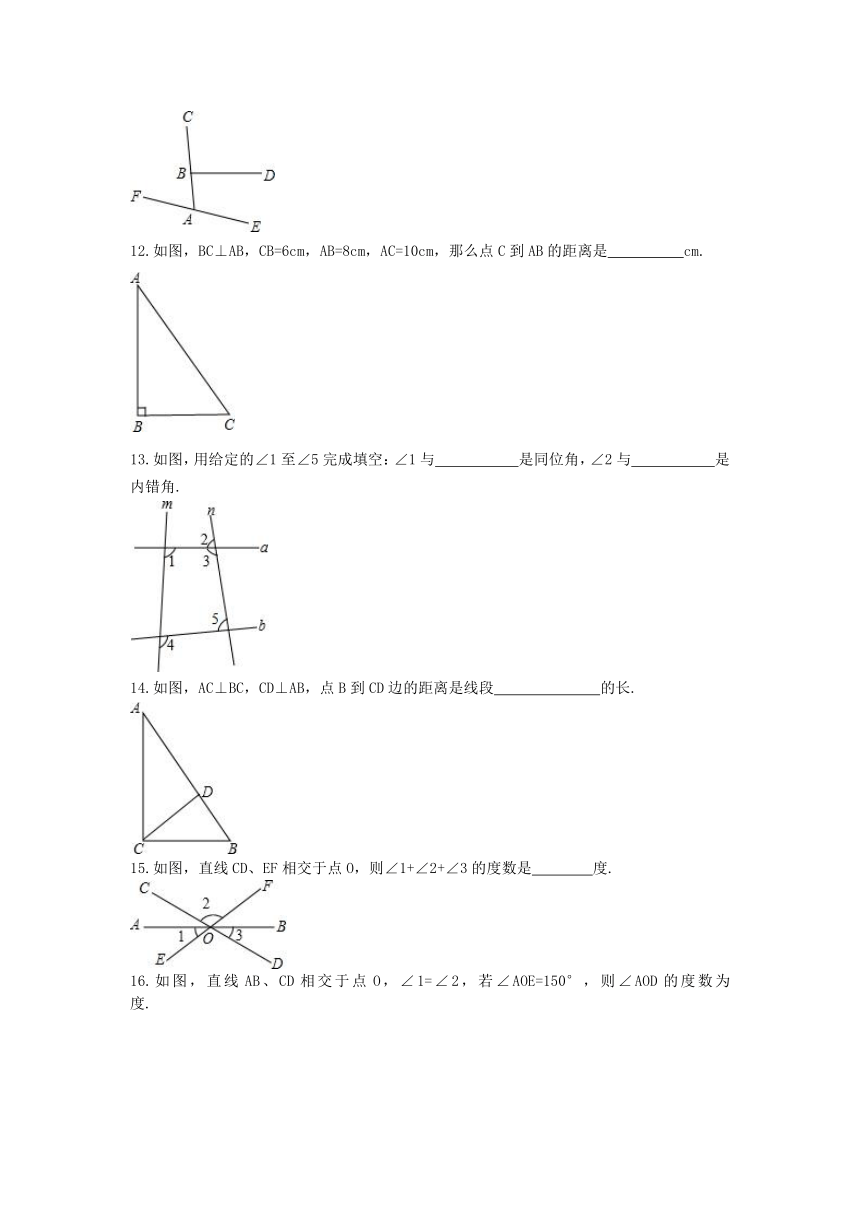
12.如图,BC⊥AB,CB=6cm,AB=8cm,AC=10cm,那么点C到AB的距离是 cm.
13.如图,用给定的∠1至∠5完成填空:∠1与 是同位角,∠2与 是内错角.
14.如图,AC⊥BC,CD⊥AB,点B到CD边的距离是线段 的长.
15.如图,直线CD、EF相交于点O,则∠1+∠2+∠3的度数是 度.
16.如图,直线AB、CD相交于点O,∠1=∠2,若∠AOE=150°,则∠AOD的度数为 度.
三、解答题(5个小题,满分44分)
17.(8分)如图,点P是∠AOB的边OB上的一点.
(1)过点P画OA的垂线,垂足为H;
(2)过点P画OB的垂线,交OA于点C;
(3)线段PH的长度是点P到 直线OA
的距离, 线段CP的长度
是点C到直线OB的距离.因为直线外一点到直线上各点连接的所有线段中,垂线段最短,所以线段PC、PH、OC这三条线段大小关系是 PH<PC<OC
.(用“<”号连接)
18.(8分)(1)如果把图看成是直线AB,EF被直线CD所截,那么∠1与∠2是一对什么角?∠2与∠3呢?
(2)如果把图看成是直线AB,CD被直线EF所截,那么∠4与∠5是一对什么角?∠5与∠6呢?
19.(9分)如图所示,直线AB、CD相交于O,OE平分∠AOD,OF⊥CD于点O,∠1=40°.
求∠2和∠3的度数.
20.(9分)如图,BE是AB的延长线,指出下面各组中的两个角是由哪两条直线被哪一条直线所截形成的?它们是什么角?
(1)∠A和∠D;
(2)∠A和∠CBA;
(3)∠C和∠CBE.
21.(10分)如图,直线AB、CD相交于点O,OM⊥AB.
(1)若∠1=∠2,求∠NOD.
(2)若∠1=∠BOC,求∠AOC与∠MOD.
参考答案
一、1.A 2.B 3.B 4.A 5.D 6.A 7.B 8.C
二、9. ∠2 10. 25° 11. ∠FAC与∠DBA 12.6 13. ∠4,∠1 14.BD 15.180 16.60
三、17. 解:(1)(2)所画图形如下所示;
(3)线段PH的长度是点P到直线OA的距离,线段CP的长度是点C到直线OB的距离,
根据垂线段最短可得:PH<PC<OC.
故答案为:直线OA,线段CP的长度,PH<PC<OC.
18. 解:(1)∠1与∠2是内错角,∠2与∠3是同旁内角;
(2)∠4与∠5是同位角,∠5与∠6是对顶角.
19. 解:因为OF⊥CD
所以∠FOC=90°.
因为∠1=40°,AB为直线,
所以∠3+∠FOC+∠1=180°,
所以∠3=180°-90°-40°=50°.
因为∠3与∠AOD互补,
所以∠AOD=180°-∠3=130°,
因为OE平分∠AOD,
所以∠2=∠AOD=65°.
20. 解:(1)∠A和∠D是由直线AE、CD被直线AD所截形成的,它们是同旁内角;
(2)∠A和∠CBA是由直线AD、BC被直线AE所截形成的,它们是同旁内角;
(3)∠C和∠CBE是由直线CD、AE被直线BC所截形成的,它们是内错角.
21. 解:(1)因为OM⊥AB,
所以∠AOM=∠1+∠AOC=90°,
因为∠1=∠2,
所以∠NOC=∠2+∠AOC=90°,
所以∠NOD=180°-∠NOC=180°-90°=90°;
(2)因为OM⊥AB,
所以∠AOM=∠BOM=90°,
因为∠1=∠BOC,
所以∠BOC=∠1+90°=3∠1,
解得∠1=45°,
所以∠AOC=90°-∠1=90°-45°=45°,
所以∠MOD=180°-∠1=180°-45°=135°.
一、选择题(每题3分,满分24分)
1.如图,在所标识的角中,互为对顶角的两个角是( )
A.∠2和∠3 B.∠1和∠3 C.∠1和∠4 D.∠1和∠2
2.已知:如图,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是( )
A.相等 B.互余 C.互补 D.互为对顶角
3.如图,直线AB、CD相交于O点,∠AOD+∠BOC=236°,则∠AOC=( )
A.72° B.62° C.124° D.144°
4.如图,有三条公路,其中AC与AB垂直,小明和小亮分别沿AC,BC同时出发骑车到C城,若他们同时到达,则下列判断中正确的是( )
A.小亮骑车的速度快 B.小明骑车的速度快
C.两人一样快 D.因为不知道公路的长度,所以无法判断他们速度的快慢
5.如图,下列说法不正确的是( )
A.∠1和∠3是对顶角 B.∠1和∠4是内错角
C.∠3和∠4是同位角 D.∠1和∠2是同旁内角
6.如图,直线AB,CD相交于点O,OM⊥AB,若∠COB=135°,则∠MOD等于( )
A.45° B.35° C.25° D.15°
7.下图中,∠1和∠2不是同旁内角的是( )
A. B. C. D.
8.如图,已知AB⊥BD,BC⊥CD,AD=a,CD=b,则BD的长的取值范围为( )
A.大于b B.小于a C.大于b且小于a D.无法确定
二、填空题(每题4分,满分32分)
9.如图,直线AB、CD被直线EF所截,则∠3的同旁内角是 .
10.用剪刀剪东西时,剪刀张开的角度如图所示,若∠1=25°,则∠2= .
11.如图,写出图中的一对内错角 .
12.如图,BC⊥AB,CB=6cm,AB=8cm,AC=10cm,那么点C到AB的距离是 cm.
13.如图,用给定的∠1至∠5完成填空:∠1与 是同位角,∠2与 是内错角.
14.如图,AC⊥BC,CD⊥AB,点B到CD边的距离是线段 的长.
15.如图,直线CD、EF相交于点O,则∠1+∠2+∠3的度数是 度.
16.如图,直线AB、CD相交于点O,∠1=∠2,若∠AOE=150°,则∠AOD的度数为 度.
三、解答题(5个小题,满分44分)
17.(8分)如图,点P是∠AOB的边OB上的一点.
(1)过点P画OA的垂线,垂足为H;
(2)过点P画OB的垂线,交OA于点C;
(3)线段PH的长度是点P到 直线OA
的距离, 线段CP的长度
是点C到直线OB的距离.因为直线外一点到直线上各点连接的所有线段中,垂线段最短,所以线段PC、PH、OC这三条线段大小关系是 PH<PC<OC
.(用“<”号连接)
18.(8分)(1)如果把图看成是直线AB,EF被直线CD所截,那么∠1与∠2是一对什么角?∠2与∠3呢?
(2)如果把图看成是直线AB,CD被直线EF所截,那么∠4与∠5是一对什么角?∠5与∠6呢?
19.(9分)如图所示,直线AB、CD相交于O,OE平分∠AOD,OF⊥CD于点O,∠1=40°.
求∠2和∠3的度数.
20.(9分)如图,BE是AB的延长线,指出下面各组中的两个角是由哪两条直线被哪一条直线所截形成的?它们是什么角?
(1)∠A和∠D;
(2)∠A和∠CBA;
(3)∠C和∠CBE.
21.(10分)如图,直线AB、CD相交于点O,OM⊥AB.
(1)若∠1=∠2,求∠NOD.
(2)若∠1=∠BOC,求∠AOC与∠MOD.
参考答案
一、1.A 2.B 3.B 4.A 5.D 6.A 7.B 8.C
二、9. ∠2 10. 25° 11. ∠FAC与∠DBA 12.6 13. ∠4,∠1 14.BD 15.180 16.60
三、17. 解:(1)(2)所画图形如下所示;
(3)线段PH的长度是点P到直线OA的距离,线段CP的长度是点C到直线OB的距离,
根据垂线段最短可得:PH<PC<OC.
故答案为:直线OA,线段CP的长度,PH<PC<OC.
18. 解:(1)∠1与∠2是内错角,∠2与∠3是同旁内角;
(2)∠4与∠5是同位角,∠5与∠6是对顶角.
19. 解:因为OF⊥CD
所以∠FOC=90°.
因为∠1=40°,AB为直线,
所以∠3+∠FOC+∠1=180°,
所以∠3=180°-90°-40°=50°.
因为∠3与∠AOD互补,
所以∠AOD=180°-∠3=130°,
因为OE平分∠AOD,
所以∠2=∠AOD=65°.
20. 解:(1)∠A和∠D是由直线AE、CD被直线AD所截形成的,它们是同旁内角;
(2)∠A和∠CBA是由直线AD、BC被直线AE所截形成的,它们是同旁内角;
(3)∠C和∠CBE是由直线CD、AE被直线BC所截形成的,它们是内错角.
21. 解:(1)因为OM⊥AB,
所以∠AOM=∠1+∠AOC=90°,
因为∠1=∠2,
所以∠NOC=∠2+∠AOC=90°,
所以∠NOD=180°-∠NOC=180°-90°=90°;
(2)因为OM⊥AB,
所以∠AOM=∠BOM=90°,
因为∠1=∠BOC,
所以∠BOC=∠1+90°=3∠1,
解得∠1=45°,
所以∠AOC=90°-∠1=90°-45°=45°,
所以∠MOD=180°-∠1=180°-45°=135°.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
