第二章 直角三角形的边角关系 5 三角函数的应用 第2课时方向角问题(含答案)
文档属性
| 名称 | 第二章 直角三角形的边角关系 5 三角函数的应用 第2课时方向角问题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 9.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-28 22:46:32 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二章 直角三角形的边角关系
5 三角函数的应用
第2课时 方向角问题
1.如图,一艘海轮位于灯塔 P 的南偏东 方向,距离灯塔 35 海里的A处,它沿正北方向航行一段时间后,到达位于灯塔的正东方向上的 B 处,这时,B处与灯塔 P 的距离PB 的长可以表示为( )
A.35海里 海里 海里 海里
第1题图 第2题图
2.“淄博烧烤”火了,许多游客纷纷从外地来到淄博吃烧烤.如图,济南的小李乘坐高铁由济南来淄博吃烧烤时,在距离铁轨200米的B处,观察他所乘坐的由济南经过淄博开往青岛的“和谐号”动车.他观察到,当“和谐号”动车车头在 A 处时,恰好位于 B处的北偏东60°方向上;10秒钟后,动车车头到达C处,恰好位于 B 处的西北方向上.小李根据所学知识求得,这时段动车的平均速度是 ( )
米/秒 米/秒 C.200米/秒 D.300米/秒
3.如图,在一笔直的海岸线上有 A,B两个观测站,A 观测站在B观测站的正东方向,有一艘小船在点 P 处,从 A 处测得小船在北偏西 60°方向上,从 B处测得小船在北偏东45°方向上,点 P 到点B 的距离是 千米.则A,B两观测站之间的距离为(结果有根号的保留根号)( )
千米 千米 C.6千米 千米
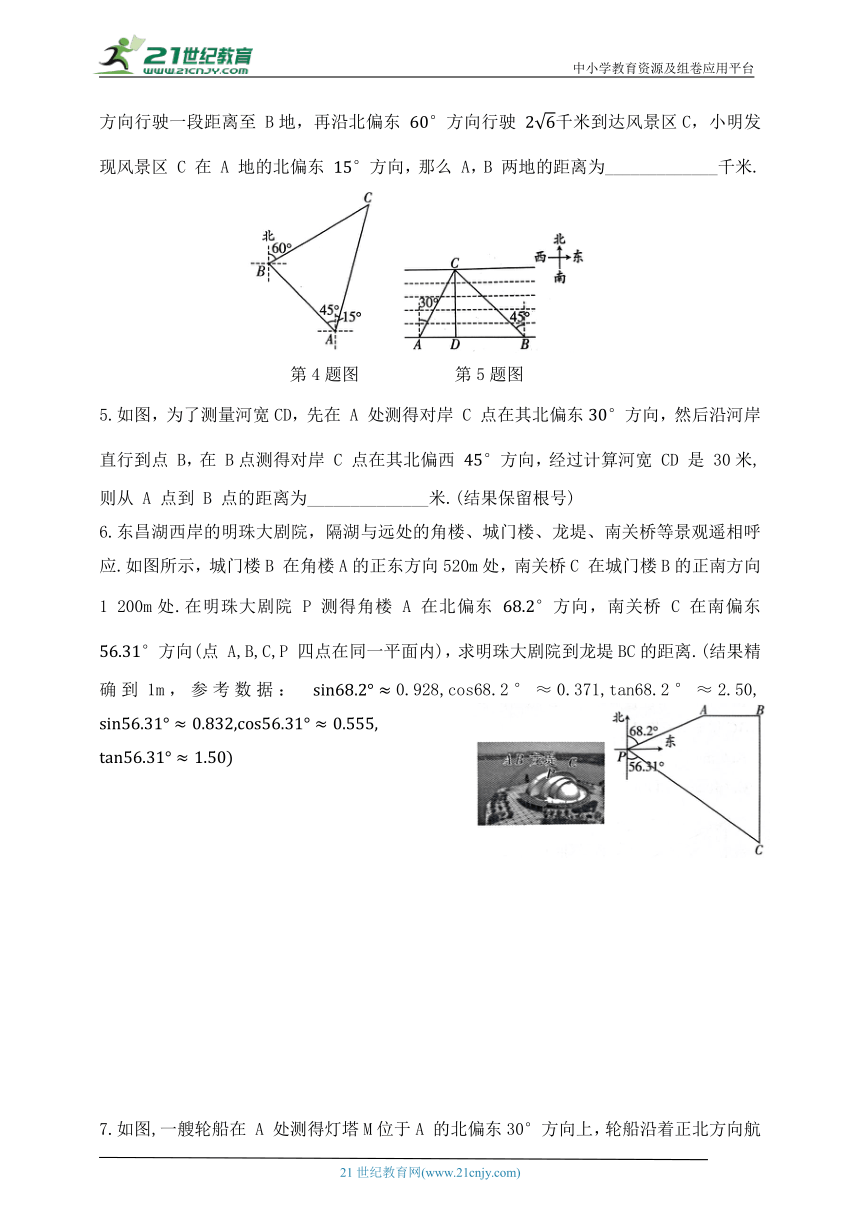
4.如图,小明一家自驾到风景区C游玩,到达 A 地后,导航显示车辆应沿北偏西 方向行驶一段距离至 B地,再沿北偏东 方向行驶 千米到达风景区C,小明发现风景区 C 在 A 地的北偏东 方向,那么 A,B 两地的距离为_____________千米.
第4题图 第5题图
5.如图,为了测量河宽CD,先在 A 处测得对岸 C 点在其北偏东方向,然后沿河岸直行到点 B,在 B点测得对岸 C 点在其北偏西 方向,经过计算河宽 CD 是 30米,则从 A 点到 B 点的距离为______________米.(结果保留根号)
6.东昌湖西岸的明珠大剧院,隔湖与远处的角楼、城门楼、龙堤、南关桥等景观遥相呼应.如图所示,城门楼B 在角楼A的正东方向520m处,南关桥C 在城门楼B的正南方向1 200m处.在明珠大剧院 P 测得角楼 A 在北偏东 方向,南关桥 C 在南偏东 方向(点 A,B,C,P 四点在同一平面内),求明珠大剧院到龙堤BC的距离.(结果精确到1m,参考数据: 0.928,cos68.2°≈0.371,tan68.2°≈2.50,
7.如图,一艘轮船在 A 处测得灯塔M位于A 的北偏东30°方向上,轮船沿着正北方向航行20海里到达 B 处,测得灯塔 M位于B 的北偏东 60°方向上,测得港口C位于 B 的北偏东 45°方向上.已知港口 C在灯塔M 的正北方向上.
(1)填空:∠AMB=_____________度,∠BCM=___________度;
(2)求灯塔 M 到轮船航线AB 的距离;(结果保留根号)
(3)求港口 C 与灯塔 M 的距离.(结果保留根号)
8.为了美化环境,提高民众的生活质量,市政府在三角形花园 ABC 边上修建一个四边形人工湖泊ABDE,并沿湖泊修建了人行步道.如图,点 C 在点 A 的正东方向 170 米处,点 E 在点 A 的正北方向,点B,D 都在点 C 的正北方向,BD 长为 100 米,点 B 在点 A 的北偏东 方向,点 D 在点 E 的北偏东! 方向.
(1)求步道 DE 的长度;
(2)点 D 处有一个小商店,某人从点 A 出发沿人行步道去商店购物,可以经点 B 到达点D,也可以经点 E 到达点 D,请通过计算说明他走哪条路较近.(结果精确到个位;参
考数据:
参考答案
1. D 2. A 3. B
4. 4
6.解:如图,过点 P 作 于点 E,过点 A 作 于点D,
则四边形 ADEB 是矩形,
设 在 中,
在 中, 解得.
答:明珠大剧院到龙堤 BC的距离约为1 320 m.
7.解:分别过点 C,M,作 CD⊥AB,ME⊥AB,垂足分别为点 D,E.
(1)∵∠DBM=∠A +∠AMB=60°,∠A=30°,∴∠AMB=30°.
∵AB,CM都是正北方向,∴AB∥CM.
∵∠DBC=45°,∴∠BCM=45°.
故答案为:30,45;
(2)由(1),得∠A=∠AMB,∴AB=BM=20海里.
在 Rt△EBM中,
(海里).
所以,灯塔 M到轮船航线AB 的距离为 海里;
(3)∵CD⊥AB,ME⊥AB,AB,CM都是正北方向,
∴四边形 DEMC 是矩形, 海里,DE=CM.
在 Rt△CDB中,∵∠DBC=45°,∴∠DBC=∠DCB. 海里.
在 Rt△EMB 中,
∴(海里), 1)海里.
所以,港口 C与灯塔 M 的距离为 海里.
8.解:(1)如图,过点 D 作. 垂足为点 F,
由题意,得四边形 ACDF 是矩形,米,
在 中, (米),
所以,步道 DE 的长度约为 200米;
(2)某人从 A 出发,经过点 B 到达点 D 路程较近,
理由:在 中, 170米,
(米),
在 中, 米,
(米),
(米),
米, 米,
∵四边形 ACDF 是矩形, 米,
288米,
∴某人从点 A出发,经过点 B到达点 D 路程=(米),
某人从点 A 出发,经过点 E 到达点 D 路程=(米),
∵440米<488 米,
∴某人从点 A 出发,经过点 B 到达点 D 路程较近.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二章 直角三角形的边角关系
5 三角函数的应用
第2课时 方向角问题
1.如图,一艘海轮位于灯塔 P 的南偏东 方向,距离灯塔 35 海里的A处,它沿正北方向航行一段时间后,到达位于灯塔的正东方向上的 B 处,这时,B处与灯塔 P 的距离PB 的长可以表示为( )
A.35海里 海里 海里 海里
第1题图 第2题图
2.“淄博烧烤”火了,许多游客纷纷从外地来到淄博吃烧烤.如图,济南的小李乘坐高铁由济南来淄博吃烧烤时,在距离铁轨200米的B处,观察他所乘坐的由济南经过淄博开往青岛的“和谐号”动车.他观察到,当“和谐号”动车车头在 A 处时,恰好位于 B处的北偏东60°方向上;10秒钟后,动车车头到达C处,恰好位于 B 处的西北方向上.小李根据所学知识求得,这时段动车的平均速度是 ( )
米/秒 米/秒 C.200米/秒 D.300米/秒
3.如图,在一笔直的海岸线上有 A,B两个观测站,A 观测站在B观测站的正东方向,有一艘小船在点 P 处,从 A 处测得小船在北偏西 60°方向上,从 B处测得小船在北偏东45°方向上,点 P 到点B 的距离是 千米.则A,B两观测站之间的距离为(结果有根号的保留根号)( )
千米 千米 C.6千米 千米
4.如图,小明一家自驾到风景区C游玩,到达 A 地后,导航显示车辆应沿北偏西 方向行驶一段距离至 B地,再沿北偏东 方向行驶 千米到达风景区C,小明发现风景区 C 在 A 地的北偏东 方向,那么 A,B 两地的距离为_____________千米.
第4题图 第5题图
5.如图,为了测量河宽CD,先在 A 处测得对岸 C 点在其北偏东方向,然后沿河岸直行到点 B,在 B点测得对岸 C 点在其北偏西 方向,经过计算河宽 CD 是 30米,则从 A 点到 B 点的距离为______________米.(结果保留根号)
6.东昌湖西岸的明珠大剧院,隔湖与远处的角楼、城门楼、龙堤、南关桥等景观遥相呼应.如图所示,城门楼B 在角楼A的正东方向520m处,南关桥C 在城门楼B的正南方向1 200m处.在明珠大剧院 P 测得角楼 A 在北偏东 方向,南关桥 C 在南偏东 方向(点 A,B,C,P 四点在同一平面内),求明珠大剧院到龙堤BC的距离.(结果精确到1m,参考数据: 0.928,cos68.2°≈0.371,tan68.2°≈2.50,
7.如图,一艘轮船在 A 处测得灯塔M位于A 的北偏东30°方向上,轮船沿着正北方向航行20海里到达 B 处,测得灯塔 M位于B 的北偏东 60°方向上,测得港口C位于 B 的北偏东 45°方向上.已知港口 C在灯塔M 的正北方向上.
(1)填空:∠AMB=_____________度,∠BCM=___________度;
(2)求灯塔 M 到轮船航线AB 的距离;(结果保留根号)
(3)求港口 C 与灯塔 M 的距离.(结果保留根号)
8.为了美化环境,提高民众的生活质量,市政府在三角形花园 ABC 边上修建一个四边形人工湖泊ABDE,并沿湖泊修建了人行步道.如图,点 C 在点 A 的正东方向 170 米处,点 E 在点 A 的正北方向,点B,D 都在点 C 的正北方向,BD 长为 100 米,点 B 在点 A 的北偏东 方向,点 D 在点 E 的北偏东! 方向.
(1)求步道 DE 的长度;
(2)点 D 处有一个小商店,某人从点 A 出发沿人行步道去商店购物,可以经点 B 到达点D,也可以经点 E 到达点 D,请通过计算说明他走哪条路较近.(结果精确到个位;参
考数据:
参考答案
1. D 2. A 3. B
4. 4
6.解:如图,过点 P 作 于点 E,过点 A 作 于点D,
则四边形 ADEB 是矩形,
设 在 中,
在 中, 解得.
答:明珠大剧院到龙堤 BC的距离约为1 320 m.
7.解:分别过点 C,M,作 CD⊥AB,ME⊥AB,垂足分别为点 D,E.
(1)∵∠DBM=∠A +∠AMB=60°,∠A=30°,∴∠AMB=30°.
∵AB,CM都是正北方向,∴AB∥CM.
∵∠DBC=45°,∴∠BCM=45°.
故答案为:30,45;
(2)由(1),得∠A=∠AMB,∴AB=BM=20海里.
在 Rt△EBM中,
(海里).
所以,灯塔 M到轮船航线AB 的距离为 海里;
(3)∵CD⊥AB,ME⊥AB,AB,CM都是正北方向,
∴四边形 DEMC 是矩形, 海里,DE=CM.
在 Rt△CDB中,∵∠DBC=45°,∴∠DBC=∠DCB. 海里.
在 Rt△EMB 中,
∴(海里), 1)海里.
所以,港口 C与灯塔 M 的距离为 海里.
8.解:(1)如图,过点 D 作. 垂足为点 F,
由题意,得四边形 ACDF 是矩形,米,
在 中, (米),
所以,步道 DE 的长度约为 200米;
(2)某人从 A 出发,经过点 B 到达点 D 路程较近,
理由:在 中, 170米,
(米),
在 中, 米,
(米),
(米),
米, 米,
∵四边形 ACDF 是矩形, 米,
288米,
∴某人从点 A出发,经过点 B到达点 D 路程=(米),
某人从点 A 出发,经过点 E 到达点 D 路程=(米),
∵440米<488 米,
∴某人从点 A 出发,经过点 B 到达点 D 路程较近.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
