人教版数学八年级上暑假预习课第十七讲 轴对称自学检测卷(含解析)
文档属性
| 名称 | 人教版数学八年级上暑假预习课第十七讲 轴对称自学检测卷(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-30 09:58:50 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版数学八年级上暑假预习课
第十七讲 轴对称自学检测卷
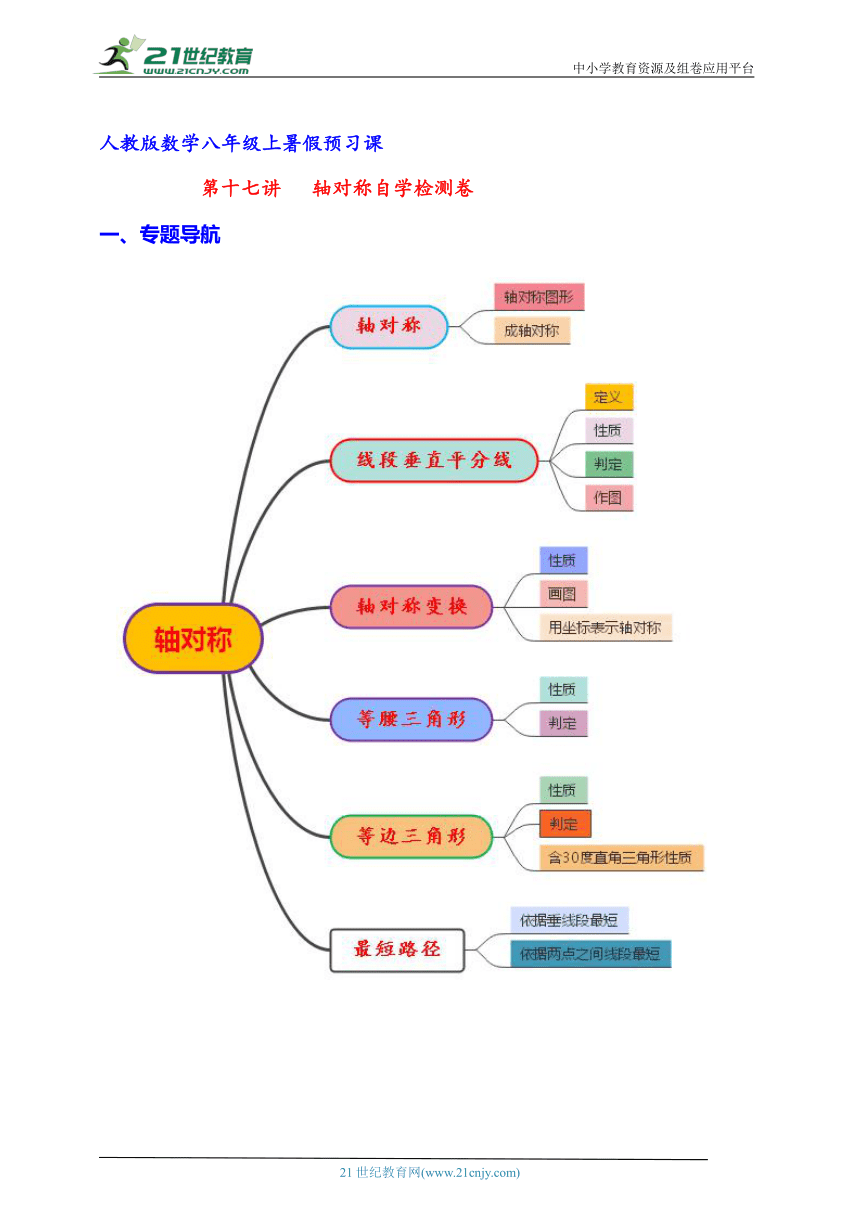
一、专题导航
轴对称自学检测卷
考试范围:13章轴对称;考试时间:120分钟;满分120分
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 总分
得分
分卷I
评卷人 得分
. .
一、选择题(共10题;共30.0分)
1.(3分)剪纸又称刻纸,是中国最古老的民间艺术之一,它是以纸为加工对象,以剪刀(或刻刀)为工具进行创作的艺术.民间剪纸往往通过谐音、象征、寓意等手法提炼、概括自然形态,构成美丽的图案.下列剪纸中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
2.(3分)如图,在△ABC中,AB=4,BC=7,DE是AC的中垂线,则△ABD的周长为( )
A. 10 B. 11 C. 12 D. 13
3.(3分)如图,△ABC与△DEF关于直线MN成轴对称,则以下结论中不一定成立的是( )
A. AB=DE B. ∠B=∠E
C. AB∥DF D. 线段AD被MN垂直平分
4.(3分)如图,两把相同的直尺的一边分别与射线OB、OA重合,另一边相交于点P,则OP平分∠BOA的依据是( )
A. 在角的内部,到角的两边距离相等的点在这个角的平分线上
B. 角平分线上的点到这个角的两边距离相等
C. 角平分线的性质
D. 角平分线是轴对称图形
5.(3分)室内墙壁上挂一平面镜,小明在平面镜内看到他背后墙上时钟的示数如图所示,则这时的实际时间应是( )
A. 3:20 B. 3:40 C. 4:40 D. 8:20
6.(3分)如图,中,是角平分线,垂足为,垂足为,与交于,下列说法不一定正确的是( )
A. 也是中线 B. 平分
C. D.
7.(3分)如图,在△ABC中,分别以点A和点C为圆心,大于的长为半径作弧(弧所在圆的半径都相等),两弧相交于M,N两点,直线MN分别与边BC,AC相交于点D,E,连接AD.若BD=DC,AE=4,AD=5,则AB的长为( )
A. 9 B. 8 C. 7 D. 6
8.(3分)如图,等腰三角形ABC底边BC的长为4 cm,面积为12 cm2,腰AB的垂直平分线EF交AB于点E,交AC于点F,若D为BC边上的中点,M为线段EF上一点,则△BDM的周长最小值为( )
A. 5 cm B. 6 cm C. 8 cm D. 10 cm
9.(3分)如图,在△ABC中,∠C=90°,BC=8、AC=6,若点P为直线BC上一点,且△ABP为等腰三角形,则符合条件的点P有( )
A. 1个 B. 2个 C. 3个 D. 4个
10.(3分)如图,在△ABC中,∠BAC和∠ABC的平分线AE,BF相交于点O,AE交BC于E,BF交AC于F,过点O作OD⊥BC于D,下列三个结论:①∠AOB=90°+∠C;②当∠C=60°时,AF+BE=AB;③若OD=a,AB+BC+CA=2b,则S△ABC=ab.其中正确的是( )
A. ①② B. ②③ C. ①②③ D. ①③
分卷II
评卷人 得分
. .
二、填空题(共5题;共15.0分)
11.(3分)如图,△AOB与△COB关于边OB所在的直线成轴对称,AO的延长线交BC于点D.若∠BOD=45°,∠C=20°,则∠ADC=_____.
12.(3分)如图,课间休息时,小新将镜子放在桌面上,无意间看到镜子中有一串数字,原来是桌旁墙面上张贴的同学手机号码中的几个数字,请问镜子中的数字对应的实际数字是_____.
13.(3分)如图,在中,,是的平分线,.若P,Q分别是和上的动点,则的最小值是_____.
14.(3分)如图,在等边三角形ABC中,AB=2,BD是AC边上的高,延长BC至点E,使CE=CD,则BE的长为_______.
15.(3分)如图,∠AOB=120°,点P为∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:①PM=PN;②OM+ON=OP;③四边形PMON的面积保持不变;④△PMN的周长保持不变.其中说法正确的是_______.(填序号)
评卷人 得分
. .
三、解答题(共8题;共75.0分)
16.(8分)如图,在△ABC中,∠ABC=70°,AB=AC=8,D为BC中点,点N在线段AD上,NM∥AC交AB于点M,BN=3.
(1)求∠CAD度数;
(2)求△BMN的周长.
17.(8分)如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(-3,1),B(2,3),C(1,0).
(1)在图中作△A'B'C',使得△A'B'C'与△ABC关于直线l轴对称.
(2)点A'的坐标为 _____,点B'的坐标为 _____.
18.(6分)已知:如图,在等腰△ABC中,AB=AC.求作:在BC边上找一点D,使得AD=CD.
小李同学在学习了尺规作图的相关知识后,设计作图步骤如下:
①分别以点A,C为圆心,大于AC长为半径作弧,两弧相交于M,N两点;
②连接MN,交BC于点D,连接AD;
③点D即为所求.
(1)请根据上述的设计方案,补全作图痕迹,并分析小李同学的作图依据是 _____;
(2)补充下面的证明过程:
证明:设MN交AC于点E,
∵MN垂直平分AC,
∴∠AED=∠CED=90°,_____,DE=DE,
∴△AED≌△CED,
∴AD=_____.( _____)(填推理依据).
19.(9分)如图,在中,垂直平分,分别交,于点、,垂直平分,分别交、于点、,连接,.
(1)若,求的周长等于__________.
(2)若,求的度数
20.(9分)阅读下面材料,并解决相应的问题:
在数学课上,老师给出如下问题,已知线段AB,求作线段AB的垂直平分线.小明的作法如下:
(1)分别以A,B为圆心,大于AB长为半径作弧,两弧交于点C;
(2)再分别以A,B为圆心,大于AB长为半径作弧,两弧交于点D;
(3)作直线CD,直线CD即为所求的垂直平分线.
同学们对小明的作法提出质疑,小明给出了这个作法的证明如下:
连接AC,BC,AD,BD.
由作图可知:AC=BC,AD=BD.
∴点C,点D在线段的垂直平分线上(依据1:_____).
∴直线就是线段的垂直平分线(依据2:_____).
(1)请你将小明证明的依据写在横线上;
(2)将小明所作图形放在如图的正方形网格中,点A,B,C,D恰好均在格点上,依次连接A,C,B,D,A各点,得到如图所示的“箭头状”的基本图形,请在网格中添加若干个此基本图形,使其各顶点也均在格点上,且与原图形组成的新图形是中心对称图形.
21.(10分)如图,.
(1)写出与的数量关系
(2)延长到,使,延长到,使,连接.求证:.
(3)在(2)的条件下,作的平分线,交于点,求证:.
22.(12分)如图所示,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.
(1)当∠BDA=115°时,∠BAD= ;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”).
(2)当DC的长为多少时,△ABD与△DCE全等?请说明理由.
(3)在点D的运动过程中,△ADE的形状也在改变,请判断当∠BDA等于多少度时,△ADE是等腰三角形.(直接写出结论,不说明理由.)
23.(13分)如图,在等边△ABC中,AB=AC=BC=10厘米,DC=4厘米,如果点M以3厘米/秒的速度运动.
(1)如果点M在线段CB上由点C向点B运动,点N在线段BA上由B点向A点运动.它们同时出发,若点N的运动速度与点M的运动速度相等.经过2秒后,△BMN和△CDM是否全等?请说明理由;
(2)在(1)的条件下,当两点的运动时间为多少时,△BMN是一个直角三角形?
(3)若点N的运动速度与点M的运动速度不相等,点N从点B出发,点M以原来的运动速度从点C同时出发,都顺时针沿△ABC三边运动,经过25秒点M与点N第一次相遇,则点N的运动速度是多少厘米/秒.
人教版数学八年级上暑假预习课
第十七讲 轴对称自学检测卷(解析版)
一、专题导航
轴对称自学检测卷
考试范围:13章轴对称;考试时间:120分钟;满分120分
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 总分
得分
分卷I
评卷人 得分
. .
一、选择题(共10题;共30.0分)
1.(3分)剪纸又称刻纸,是中国最古老的民间艺术之一,它是以纸为加工对象,以剪刀(或刻刀)为工具进行创作的艺术.民间剪纸往往通过谐音、象征、寓意等手法提炼、概括自然形态,构成美丽的图案.下列剪纸中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
【答案】C
【解析】根据轴对称图形和中心对称图形的定义进行逐一判断即可.
解:A.原图是中心对称图形,不是轴对称图形,不符合题意;
B.原图是轴对称图形,不是中心对称图形,不符合题意;
C.原图既是中心对称图形,又是轴对称图形,符合题意;
D.原图是轴对称图形,不是中心对称图形,不符合题意;
故选:C.
2.(3分)如图,在△ABC中,AB=4,BC=7,DE是AC的中垂线,则△ABD的周长为( )
A. 10 B. 11 C. 12 D. 13
【答案】B
【解析】根据线段垂直平分线的性质得到DA=DC,再根据三角形的周长公式计算,得到答案.
解:∵DE是AC的中垂线,
∴DA=DC,
∴△ABD的周长=AB+BD+DA=AB+BD+DC=AB+BC,
∵AB=4,BC=7,
∴△ABD的周长=4+7=11,
故选:B.
3.(3分)如图,△ABC与△DEF关于直线MN成轴对称,则以下结论中不一定成立的是( )
A. AB=DE B. ∠B=∠E
C. AB∥DF D. 线段AD被MN垂直平分
【答案】C
【解析】根据轴对称的性质作答.
解:A、AB=DE,成立,不符合题意;
B、∠B=∠E,成立,不符合题意;
C、AB与DF不一定平行,不成立,符合题意;
D、线段AD被MN垂直平分,成立,不符合题意.
故选:C.
4.(3分)如图,两把相同的直尺的一边分别与射线OB、OA重合,另一边相交于点P,则OP平分∠BOA的依据是( )
A. 在角的内部,到角的两边距离相等的点在这个角的平分线上
B. 角平分线上的点到这个角的两边距离相等
C. 角平分线的性质
D. 角平分线是轴对称图形
【答案】A
【解析】过两把直尺的交点P作PE⊥AO,PF⊥BO,根据题意可得PE=PF,再根据角的内部到角的两边的距离相等的点在这个角的平分线上,可得OP平分∠AOB.
解:如图所示:PE⊥AO,过两把直尺的交点P作PF⊥BO,
∵两把完全相同的长方形直尺,
∴PE=PF,
∴OP平分∠AOB(角的内部到角的两边的距离相等的点在这个角的平分线上),
故选:A.
5.(3分)室内墙壁上挂一平面镜,小明在平面镜内看到他背后墙上时钟的示数如图所示,则这时的实际时间应是( )
A. 3:20 B. 3:40 C. 4:40 D. 8:20
【答案】B
【解析】根据镜面对称的性质,在平面镜中的像与现实中的事物恰好左右颠倒,且关于镜面对称,分析并作答.
解:根据镜面对称的性质,分析可得题中所显示的时刻与3:40成轴对称,所以此时实际时刻为3:40.
故选:B.
6.(3分)如图,中,是角平分线,垂足为,垂足为,与交于,下列说法不一定正确的是( )
A. 也是中线 B. 平分
C. D.
【答案】A
【解析】A.根据等腰三角形的三线合一可以判定A符合题意;
B.根据角平分线的性质得出,证明,得出,即可判断B不符合题意;
CD.根据全等三角形的性质得出,根据,证明垂直平分,即可判断CD不符合题意.
解:A.等腰三角形底边上的中线,顶角平分线,底边上的高线才三线合一,而不是等腰三角形,因此不一定是中线,故A符合题意;
B.∵是角平分线,,,
∴,
∵,
∴,
∴,
∴平分,故B不符合题意;
CD.∵,
∴,
∵,
∴垂直平分,
∴,,故CD不符合题意.
故选:A.
【点睛】本题主要考查了角平分线的性质,垂直平分线的判定,等腰三角形的性质,三角形全等的判定和性质,解题的关键是熟练掌握角平分线上的点到角的两边距离相等.
7.(3分)如图,在△ABC中,分别以点A和点C为圆心,大于的长为半径作弧(弧所在圆的半径都相等),两弧相交于M,N两点,直线MN分别与边BC,AC相交于点D,E,连接AD.若BD=DC,AE=4,AD=5,则AB的长为( )
A. 9 B. 8 C. 7 D. 6
【答案】D
【解析】根据线段垂直平分线的性质可得AC=2AE=8,DA=DC,从而可得∠DAC=∠C,再结合已知易得BD=AD,从而可得∠B=∠BAD,然后利用三角形内角和定理可得∠BAC=90°,从而在Rt△ABC中,利用勾股定理进行计算,即可解答.
解:由题意得:MN是AC的垂直平分线,
∴AC=2AE=8,DA=DC,
∴∠DAC=∠C,
∵BD=CD,
∴BD=AD,
∴∠B=∠BAD,
∵∠B+∠BAD+∠C+∠DAC=180°,
∴2∠BAD+2∠DAC=180°,
∴∠BAD+∠DAC=90°,
∴∠BAC=90°,
在Rt△ABC中,BC=BD+CD=2AD=10,
∴AB===6,
故选:D.
8.(3分)如图,等腰三角形ABC底边BC的长为4 cm,面积为12 cm2,腰AB的垂直平分线EF交AB于点E,交AC于点F,若D为BC边上的中点,M为线段EF上一点,则△BDM的周长最小值为( )
A. 5 cm B. 6 cm C. 8 cm D. 10 cm
【答案】C
【解析】连接AD,由于△ABC是等腰三角形,点D是BC边的中点,故AD⊥BC,再根据三角形的面积公式求出AD的长,再根据EF是线段AB的垂直平分线可知,点B关于直线EF的对称点为点A,故AD的长为BM+MD的最小值,由此即可得出结论.
如图,连接AD.
∵△ABC是等腰三角形,点D是BC边的中点,∴AD⊥BC,∴S△ABC=BC AD=×4×AD=12,解得:AD=6(cm).
∵EF是线段AB的垂直平分线,∴点B关于直线EF的对称点为点A,∴AD的长为BM+MD的最小值,∴△BDM的周长最短=(BM+MD)+BD=AD+BC=6+×4=6+2=8(cm).
故选C.
【点睛】本题考查的是轴对称﹣最短路线问题,熟知等腰三角形三线合一的性质是解答此题的关键.
9.(3分)如图,在△ABC中,∠C=90°,BC=8、AC=6,若点P为直线BC上一点,且△ABP为等腰三角形,则符合条件的点P有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】依据点P为直线BC上一点,且△ABP为等腰三角形,需要分三种情况进行讨论,即①AB=AP,②BA=BP,③AP=BP,据此通过画图即可得出点P的位置.
解:如图所示,分别以A,B为圆心,AB的长为半径画弧,与直线l的交点P1,P2,P3即为所求;作AB的垂直平分线,与直线l的交点P4即为所求.
∴符合条件的点P有4个.
故选:D.
10.(3分)如图,在△ABC中,∠BAC和∠ABC的平分线AE,BF相交于点O,AE交BC于E,BF交AC于F,过点O作OD⊥BC于D,下列三个结论:①∠AOB=90°+∠C;②当∠C=60°时,AF+BE=AB;③若OD=a,AB+BC+CA=2b,则S△ABC=ab.其中正确的是( )
A. ①② B. ②③ C. ①②③ D. ①③
【答案】C
【解析】由角平分线的定义结合三角形的内角和的可求解∠AOB与∠C的关系,进而判定①;在AB上取一点H,使BH=BE,证得△HBO≌△EBO,得到∠BOH=∠BOE=60°,再证得△HAO≌△FAO,得到AF=AH,进而判定②正确;作OH⊥AC于H,OM⊥AB于M,根据三角形的面积可证得③正确.
解:∵∠BAC和∠ABC的平分线相交于点O,
∴∠OBA=∠CBA,∠OAB=∠CAB,
∴∠AOB=180°-∠OBA-∠OAB=180°-∠CBA-∠CAB=180°-(180°-∠C)=90°+∠C,①正确;
∵∠C=60°,
∴∠BAC+∠ABC=120°,
∵AE,BF分别是∠BAC与ABC的平分线,
∴∠OAB+∠OBA=(∠BAC+∠ABC)=60°,
∴∠AOB=120°,
∴∠AOF=60°,
∴∠BOE=60°,
如图,在AB上取一点H,使BH=BE,
∵BF是∠ABC的角平分线,
∴∠HBO=∠EBO,
在△HBO和△EBO中,,
∴△HBO≌△EBO(SAS),
∴∠BOH=∠BOE=60°,
∴∠AOH=180°-60°-60°=60°,
∴∠AOH=∠AOF,
在△HAO和△FAO中,,
∴△HAO≌△FAO(ASA),
∴AF=AH,
∴AB=BH+AH=BE+AF,故②正确;
作OH⊥AC于H,OM⊥AB于M,
∵∠BAC和∠ABC的平分线相交于点O,
∴点O在∠C的平分线上,
∴OH=OM=OD=a,
∵AB+AC+BC=2b
∴S△ABC=×AB×OM+×AC×OH+×BC×OD=(AB+AC+BC) a=ab,③正确.
故选:C.
分卷II
评卷人 得分
. .
二、填空题(共5题;共15.0分)
11.(3分)如图,△AOB与△COB关于边OB所在的直线成轴对称,AO的延长线交BC于点D.若∠BOD=45°,∠C=20°,则∠ADC=_____.
【答案】70°
【解析】根据对称性得出∠BOC=∠AOB=180°-∠BOD=135°,∠COD=∠BOC-∠BOD=135°-45°=90°,根据三角形内角和得出结论即可.
解:∵△AOB与△COB关于边OB所在的直线成轴对称,
∴∠BOC=∠AOB=180°-∠BOD=135°,∠COD=∠BOC-∠BOD=135°-45°=90°,
∴∠ADC=180°-∠C-∠COD=180°-20°-90°=70°,
故答案为:70°.
12.(3分)如图,课间休息时,小新将镜子放在桌面上,无意间看到镜子中有一串数字,原来是桌旁墙面上张贴的同学手机号码中的几个数字,请问镜子中的数字对应的实际数字是_____.
【答案】630085
【解析】易得所求的数字与看到的数字关于竖直的一条直线成轴对称,作出相应图形即可求解.
解:做轴对称图形得:|630085,
故答案是:630085.
13.(3分)如图,在中,,是的平分线,.若P,Q分别是和上的动点,则的最小值是_____.
【答案】
【解析】根据等腰三角形三线合一的性质得出,过点B作于点Q,交于点P,则此时取最小值,最小值为的长,然后利用三角形等面积法求解即可.
解:∵,是的平分线,
∴垂直平分,
∴.
过点B作于点Q,交于点P,则此时取最小值,最小值为的长,如图所示.
∵,
∴=,
即的最小值是.
故答案为:.
【点睛】题目主要考查等腰三角形的性质及三角形等面积法,最短距离问题,理解题意,熟练掌握等腰三角形的性质是解题关键.
14.(3分)如图,在等边三角形ABC中,AB=2,BD是AC边上的高,延长BC至点E,使CE=CD,则BE的长为_______.
【答案】3
【解析】由等边三角形的性质可得AC=BC=AB=2,根据BD是AC边上的高,可得AD=CD=1,再由题中条件CE=CD,即可求得BE.
解:∵△ABC是等边三角形,
∴AC=BC=AB=2,
∵BD是AC边上的高,
∴D为AC的中点,
∴AD=CD=AC=1,
∴CE=CD=1,
∴BE=BC+CE=2+1=3.
故答案为:3.
【点睛】本题考查了等边三角形的性质,等腰三角形的性质,考查了学生综合运用数学知识的能力,得到AD=CD=AC是正确解答本题的关键.
15.(3分)如图,∠AOB=120°,点P为∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:①PM=PN;②OM+ON=OP;③四边形PMON的面积保持不变;④△PMN的周长保持不变.其中说法正确的是_______.(填序号)
【答案】①②③
【解析】作PE⊥OA于E,PF⊥OB于F,根据题意得:∠EPM=∠FPN,再根据角平分线的性质定理可得PE=PF,从而得到Rt△POE≌Rt△POF,进而得到OE=OF,可得到△PEM≌△PFN,从而得到∠PEM=∠PFN,EM=NF,PM=PN,可得S△PEM=S△PFN,OM+ON= 2OE,从而得到①②③正确,再由M,N的位置变化,可得MN的长度是变化的,再证得△PMN是等边三角形,可得故④错误,即可求解.
解:如图,作PE⊥OA于E,PF⊥OB于F,
∵∠PEO=∠PFO=90°,
∴∠EPF+∠AOB=180°,
∵∠MPN+∠AOB=180°,
∴∠EPF=∠MPN,
∴∠EPM=∠FPN,
∵OP平分∠AOB,PE⊥OA,PF⊥OB,
∴PE=PF,
在Rt△POE和Rt△POF中,
∵OP=OP,PE=PF,
∴Rt△POE≌Rt△POF(HL),
∴OE=OF,
在△PEM和△PFN中,
∵∠MPE=∠NPF, PE=PF,∠PEM=∠PFN,
∴△PEM≌△PFN(ASA),
∴∠PEM=∠PFN,EM=NF,PM=PN,故①正确;
∴S△PEM=S△PFN,
∴S四边形PMON=S四边形PEOF=定值,故③正确;
∵OM+ON=OE+ME+OF-NF=2OE=定值,故②正确;
∵M,N的位置变化,
∴MN的长度是变化的,
∵PM=PN,∠MPN=60°,
∴△PMN是等边三角形,
∴△PMN的周长是变化的,故④错误,
∴说法正确的有①②③.
故答案为:①②③
【点睛】本题主要考查了全等三角形的判定和性质,角平分线的性质定理,等边三角形判定和性质等知识,熟练掌握全等三角形的判定和性质,角平分线的性质定理,等边三角形判定和性质等知识是解题的关键.
评卷人 得分
. .
三、解答题(共8题;共75.0分)
16.(8分)如图,在△ABC中,∠ABC=70°,AB=AC=8,D为BC中点,点N在线段AD上,NM∥AC交AB于点M,BN=3.
(1)求∠CAD度数;
(2)求△BMN的周长.
【解析】(1)由等腰三角形性质和三角形内角和定理可求出∠CAD度数;
(2)由平行线的性质及等腰三角形性质可得到AM=NM,则求△BMN的周长可转化成求线段AB和线段BN的和,由题中给出的条件即可求出结果.
解:(1)∵AB=AC,
∴△ABC是等腰三角形,
又∵∠ABC=70°,
∴∠BAC=180°-70°×2=40°,
又∵D为BC的中点,
∴AD平分∠BAC,
∴∠CAD=∠BAD=∠BAC=×40°=20°,
故∠CAD度数为20°.
(2)∵NM∥AC,
∴∠ANM=∠CAD,
又∵∠CAD=∠BAD,
∴∠ANM=∠BAD,
∴AM=NM,
∴△BMN的周长=MB+BN+NM=AB+BN,
∵AB=8,BN=3,
∴△BMN的周长=8+3=11.
故△BMN的周长为11.
17.(8分)如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(-3,1),B(2,3),C(1,0).
(1)在图中作△A'B'C',使得△A'B'C'与△ABC关于直线l轴对称.
(2)点A'的坐标为 _____,点B'的坐标为 _____.
【答案】(1)(-3,-3);(2)(2,-5);
【解析】(1)根据轴对称的性质作图即可.
(2)由图可得答案.
解:(1)如图,△A'B'C'即为所求.
(2)由图可得,A'(-3,-3),B'(2,-5).
故答案为:(-3,-3);(2,-5).
18.(6分)已知:如图,在等腰△ABC中,AB=AC.求作:在BC边上找一点D,使得AD=CD.
小李同学在学习了尺规作图的相关知识后,设计作图步骤如下:
①分别以点A,C为圆心,大于AC长为半径作弧,两弧相交于M,N两点;
②连接MN,交BC于点D,连接AD;
③点D即为所求.
(1)请根据上述的设计方案,补全作图痕迹,并分析小李同学的作图依据是 _____;
(2)补充下面的证明过程:
证明:设MN交AC于点E,
∵MN垂直平分AC,
∴∠AED=∠CED=90°,_____,DE=DE,
∴△AED≌△CED,
∴AD=_____.( _____)(填推理依据).
【答案】(1)线段垂直平分线上的点到线段两端点的距离相等;(2)垂直的定义;(3)CD;(4)线段垂直平分线上的点到线段两端点的距离相等;
【解析】(1)根据线段垂直平分线的性质作出图形即可;
(2)根据线段垂直平分线的性质即可得到结论.
解:(1)如图所示,
作图依据是线段垂直平分线上的点到线段两端点的距离相等;
故答案为:线段垂直平分线上的点到线段两端点的距离相等;
(2)证明:设MN交AC于点E,
∵MN垂直平分AC,
∴∠AED=∠CED=90°,(垂直的定义)DE=DE,
∴△AED≌△CED,
∴AD=CD.( 线段垂直平分线上的点到线段两端点的距离相等)(填推理依据).
故答案为:垂直的定义,CD,线段垂直平分线上的点到线段两端点的距离相等.
19.(9分)如图,在中,垂直平分,分别交,于点、,垂直平分,分别交、于点、,连接,.
(1)若,求的周长等于__________.
(2)若,求的度数
【答案】(1)9 (2)见解析
【解析】(1)根据垂直平分线的性质得出,,根据三角形周长公式即可求解;
(2)根据三角形内角和定理求得,根据垂直平分线的性质以及等边对等角可得, ,进而根据三角形内角和定理即可求解.
【小问1详解】
解:∵是的垂直平分线,
∴,
∵是的垂直平分线,
∴,
∴的周长为.
【小问2详解】
解:∵,
∴,
∵是的垂直平分线,
∴,
∴,
同理可得:,
∴,
∴.
【点睛】本题考查了垂直平分线的性质,等边对等角,三角形内角和定理,掌握以上知识是解题的关键.
20.(9分)阅读下面材料,并解决相应的问题:
在数学课上,老师给出如下问题,已知线段AB,求作线段AB的垂直平分线.小明的作法如下:
(1)分别以A,B为圆心,大于AB长为半径作弧,两弧交于点C;
(2)再分别以A,B为圆心,大于AB长为半径作弧,两弧交于点D;
(3)作直线CD,直线CD即为所求的垂直平分线.
同学们对小明的作法提出质疑,小明给出了这个作法的证明如下:
连接AC,BC,AD,BD.
由作图可知:AC=BC,AD=BD.
∴点C,点D在线段的垂直平分线上(依据1:_____).
∴直线就是线段的垂直平分线(依据2:_____).
(1)请你将小明证明的依据写在横线上;
(2)将小明所作图形放在如图的正方形网格中,点A,B,C,D恰好均在格点上,依次连接A,C,B,D,A各点,得到如图所示的“箭头状”的基本图形,请在网格中添加若干个此基本图形,使其各顶点也均在格点上,且与原图形组成的新图形是中心对称图形.
【答案】(1)到线段两个端点距离相等的点在这条线段的垂直平分线上;(2)两点确定一条直线;
【解析】(1)根据线段的垂直平分线的判定和性质判断即可.
(2)作点C,D关于AB的对称点C′,D′,连接AC′,BC′,AD′,BD′即可.
解:(1)连接AC,CB,AD,DB.
由作图可知:AC=BC,AD=BD.
∴点C,点D在线段的垂直平分线上(到线段两个端点距离相等的点在这条线段的垂直平分线上).
∴直线就是线段的垂直平分线(两点确定一条直线).
故答案为:线段的垂直平分线的性质,两点确定一条直线.
(2)如图所示:
21.(10分)如图,.
(1)写出与的数量关系
(2)延长到,使,延长到,使,连接.求证:.
(3)在(2)的条件下,作的平分线,交于点,求证:.
【答案】(1),
(2)见解析 (3)见解析
【解析】(1)勾股定理求得,结合已知条件即可求解;
(2)根据题意画出图形,证明,得出,则,即可得证;
(3)延长交于点,延长交于点,根据角平分线以及平行线的性质证明,进而证明,即可得证.
【小问1详解】
解:∵
∴,
∵
∴
即;
【小问2详解】
证明:如图所示,
∴
∴,
∵,
∴
∵,,
∴
∴
∴
∴
【小问3详解】
证明:如图所示,延长交于点,延长交于点,
∵,,
∴,
∴
∵是的角平分线,
∴,
∴
∴
∵,
∴,,
∴,
又∵,
∴,
即,
∴,
又,则,
在中,
,
∴,
∴
【点睛】本题考查了全等三角形的性质与判定,等腰三角形的性质与判定,勾股定理,平行线的性质与判定,熟练掌握全等三角形的性质与判定是解题的关键.
22.(12分)如图所示,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.
(1)当∠BDA=115°时,∠BAD= ;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”).
(2)当DC的长为多少时,△ABD与△DCE全等?请说明理由.
(3)在点D的运动过程中,△ADE的形状也在改变,请判断当∠BDA等于多少度时,△ADE是等腰三角形.(直接写出结论,不说明理由.)
【答案】(1)25°;小;
(2)DC=2,理由见解答过程;
(3)110°或80°.
【解析】(1)根据三角形内角和定理计算求出∠BAD,根据点D从点B向点C运动可以得出∠BDA逐渐变小;
(2)当DC=2时,AB=DC,根据∠DEC+∠EDC=140°,∠ADB+∠EDC=140°,得到∠ADB=∠DEC,利用AAS定理证明△ABD≌△DCE即可;
(3)分DA=DE、AE=AD、EA=ED三种情况,根据等腰三角形的性质、三角形内角和定理计算.
【小问1详解】
解:∵∠B=40°,∠BDA=115°,
∴∠BAD=180°-∠B-∠BDA=180°-115°-40°=25°,
由图形可知,∠BDA逐渐变小,
故答案为:25°;小;
【小问2详解】
当DC=2时,△ABD≌△DCE,
理由如下:∵AB=2,
∴AB=DC,
∵AB=AC,
∴∠C=∠B=40°,
∴∠DEC+∠EDC=140°,
∵∠ADE=40°,
∴∠ADB+∠EDC=140°,
∴∠ADB=∠DEC,
在△ABD和△DCE中,
∴△ABD≌△DCE(AAS);
【小问3详解】
当∠BDA的度数为110°或80°时,△ADE是等腰三角形,理由如下:
当DA=DE时,∠DAE=∠DEA=70°,
∴∠BDA=∠DAE+∠C=70°+40°=110°;
当AD=AE时,∠AED=∠ADE=40°,
∴∠DAE=100°,
此时,点D与点B重合,不合题意;
当EA=ED时,∠EAD=∠ADE=40°,
∴∠BDA=∠DAE+∠C=40°+40°=80°,
综上所述,当∠BDA的度数为110°或80°时,△ADE是等腰三角形.
【点睛】本题考查的是等腰三角形的判定与性质、全等三角形的判定与性质、三角形外角的性质,掌握全等三角形的判定定理和性质定理、灵活运用分情况讨论思想是解题的关键.
23.(13分)如图,在等边△ABC中,AB=AC=BC=10厘米,DC=4厘米,如果点M以3厘米/秒的速度运动.
(1)如果点M在线段CB上由点C向点B运动,点N在线段BA上由B点向A点运动.它们同时出发,若点N的运动速度与点M的运动速度相等.经过2秒后,△BMN和△CDM是否全等?请说明理由;
(2)在(1)的条件下,当两点的运动时间为多少时,△BMN是一个直角三角形?
(3)若点N的运动速度与点M的运动速度不相等,点N从点B出发,点M以原来的运动速度从点C同时出发,都顺时针沿△ABC三边运动,经过25秒点M与点N第一次相遇,则点N的运动速度是多少厘米/秒.
【解析】(1)由题意得到BM,BN,CM的长度,利用边角边公理即可判定结论;
(2分两种情形讨论解答:①当∠BNM=90°时;②当∠BMN=90°时,设两点的运动时为t秒,分别表示出BM,BN的长度,所对的直角边等于斜边的一半列出方程即可求出对应的时间;
(3)分两种情况解答:①当点N的速度小于点M的速度时;②当点N的速度大于点M的速度时,设点N速度为s厘米/秒,利用点M与点N第一次相遇时的路程的差列出方程即可求解.
解:(1)△BMN和△CDM全等.理由:
∵点N的运动速度与点M的运动速度相等,点M以3厘米/秒的速度运动,
∴点N的速度是3厘米/秒.
∴经过2秒后,CM=6厘米,BN=6厘米,
∴CM=BN,
∴BM=BC-CM=10-6=4(厘米).
∵DC=4厘米,
∴BM=CD.
∵AB=AC=BC,
∴∠B=∠C=60°.
在△BMN和△CDM中,
,
∴△BMN△CDM(SAS).
(2)设两点的运动时为t秒,则CM=BN=3t厘米,
∴BM=BC-CM=(10-3t)厘米.
①当∠BNM=90°时,
∵∠B=60°,
∴∠BMN=30°.
∴BN=BM.
∴3t=(10-3t).
解得:t=.
②当∠BMN=90°时,
∵∠B=60°,
∴∠BMN=30°.
∴BM=BN,
∴10-3t=×3t.
解得:t=.
综上,当两点的运动时间为秒或秒时,△BMN是一个直角三角形.
(3)设点N速度为s厘米/秒,则点N25秒运动的距离为25s厘米,
①当点N的速度小于点M的速度时,由题意得:
25×3-25s=10,
解得:s=.
②当点N的速度大于点M的速度时,由题意得:
25s-25×3=20.
解得:s=.
综上,经过25秒点M与点N第一次相遇,则点N的运动速度是厘米/秒或米/秒.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版数学八年级上暑假预习课
第十七讲 轴对称自学检测卷
一、专题导航
轴对称自学检测卷
考试范围:13章轴对称;考试时间:120分钟;满分120分
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 总分
得分
分卷I
评卷人 得分
. .
一、选择题(共10题;共30.0分)
1.(3分)剪纸又称刻纸,是中国最古老的民间艺术之一,它是以纸为加工对象,以剪刀(或刻刀)为工具进行创作的艺术.民间剪纸往往通过谐音、象征、寓意等手法提炼、概括自然形态,构成美丽的图案.下列剪纸中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
2.(3分)如图,在△ABC中,AB=4,BC=7,DE是AC的中垂线,则△ABD的周长为( )
A. 10 B. 11 C. 12 D. 13
3.(3分)如图,△ABC与△DEF关于直线MN成轴对称,则以下结论中不一定成立的是( )
A. AB=DE B. ∠B=∠E
C. AB∥DF D. 线段AD被MN垂直平分
4.(3分)如图,两把相同的直尺的一边分别与射线OB、OA重合,另一边相交于点P,则OP平分∠BOA的依据是( )
A. 在角的内部,到角的两边距离相等的点在这个角的平分线上
B. 角平分线上的点到这个角的两边距离相等
C. 角平分线的性质
D. 角平分线是轴对称图形
5.(3分)室内墙壁上挂一平面镜,小明在平面镜内看到他背后墙上时钟的示数如图所示,则这时的实际时间应是( )
A. 3:20 B. 3:40 C. 4:40 D. 8:20
6.(3分)如图,中,是角平分线,垂足为,垂足为,与交于,下列说法不一定正确的是( )
A. 也是中线 B. 平分
C. D.
7.(3分)如图,在△ABC中,分别以点A和点C为圆心,大于的长为半径作弧(弧所在圆的半径都相等),两弧相交于M,N两点,直线MN分别与边BC,AC相交于点D,E,连接AD.若BD=DC,AE=4,AD=5,则AB的长为( )
A. 9 B. 8 C. 7 D. 6
8.(3分)如图,等腰三角形ABC底边BC的长为4 cm,面积为12 cm2,腰AB的垂直平分线EF交AB于点E,交AC于点F,若D为BC边上的中点,M为线段EF上一点,则△BDM的周长最小值为( )
A. 5 cm B. 6 cm C. 8 cm D. 10 cm
9.(3分)如图,在△ABC中,∠C=90°,BC=8、AC=6,若点P为直线BC上一点,且△ABP为等腰三角形,则符合条件的点P有( )
A. 1个 B. 2个 C. 3个 D. 4个
10.(3分)如图,在△ABC中,∠BAC和∠ABC的平分线AE,BF相交于点O,AE交BC于E,BF交AC于F,过点O作OD⊥BC于D,下列三个结论:①∠AOB=90°+∠C;②当∠C=60°时,AF+BE=AB;③若OD=a,AB+BC+CA=2b,则S△ABC=ab.其中正确的是( )
A. ①② B. ②③ C. ①②③ D. ①③
分卷II
评卷人 得分
. .
二、填空题(共5题;共15.0分)
11.(3分)如图,△AOB与△COB关于边OB所在的直线成轴对称,AO的延长线交BC于点D.若∠BOD=45°,∠C=20°,则∠ADC=_____.
12.(3分)如图,课间休息时,小新将镜子放在桌面上,无意间看到镜子中有一串数字,原来是桌旁墙面上张贴的同学手机号码中的几个数字,请问镜子中的数字对应的实际数字是_____.
13.(3分)如图,在中,,是的平分线,.若P,Q分别是和上的动点,则的最小值是_____.
14.(3分)如图,在等边三角形ABC中,AB=2,BD是AC边上的高,延长BC至点E,使CE=CD,则BE的长为_______.
15.(3分)如图,∠AOB=120°,点P为∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:①PM=PN;②OM+ON=OP;③四边形PMON的面积保持不变;④△PMN的周长保持不变.其中说法正确的是_______.(填序号)
评卷人 得分
. .
三、解答题(共8题;共75.0分)
16.(8分)如图,在△ABC中,∠ABC=70°,AB=AC=8,D为BC中点,点N在线段AD上,NM∥AC交AB于点M,BN=3.
(1)求∠CAD度数;
(2)求△BMN的周长.
17.(8分)如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(-3,1),B(2,3),C(1,0).
(1)在图中作△A'B'C',使得△A'B'C'与△ABC关于直线l轴对称.
(2)点A'的坐标为 _____,点B'的坐标为 _____.
18.(6分)已知:如图,在等腰△ABC中,AB=AC.求作:在BC边上找一点D,使得AD=CD.
小李同学在学习了尺规作图的相关知识后,设计作图步骤如下:
①分别以点A,C为圆心,大于AC长为半径作弧,两弧相交于M,N两点;
②连接MN,交BC于点D,连接AD;
③点D即为所求.
(1)请根据上述的设计方案,补全作图痕迹,并分析小李同学的作图依据是 _____;
(2)补充下面的证明过程:
证明:设MN交AC于点E,
∵MN垂直平分AC,
∴∠AED=∠CED=90°,_____,DE=DE,
∴△AED≌△CED,
∴AD=_____.( _____)(填推理依据).
19.(9分)如图,在中,垂直平分,分别交,于点、,垂直平分,分别交、于点、,连接,.
(1)若,求的周长等于__________.
(2)若,求的度数
20.(9分)阅读下面材料,并解决相应的问题:
在数学课上,老师给出如下问题,已知线段AB,求作线段AB的垂直平分线.小明的作法如下:
(1)分别以A,B为圆心,大于AB长为半径作弧,两弧交于点C;
(2)再分别以A,B为圆心,大于AB长为半径作弧,两弧交于点D;
(3)作直线CD,直线CD即为所求的垂直平分线.
同学们对小明的作法提出质疑,小明给出了这个作法的证明如下:
连接AC,BC,AD,BD.
由作图可知:AC=BC,AD=BD.
∴点C,点D在线段的垂直平分线上(依据1:_____).
∴直线就是线段的垂直平分线(依据2:_____).
(1)请你将小明证明的依据写在横线上;
(2)将小明所作图形放在如图的正方形网格中,点A,B,C,D恰好均在格点上,依次连接A,C,B,D,A各点,得到如图所示的“箭头状”的基本图形,请在网格中添加若干个此基本图形,使其各顶点也均在格点上,且与原图形组成的新图形是中心对称图形.
21.(10分)如图,.
(1)写出与的数量关系
(2)延长到,使,延长到,使,连接.求证:.
(3)在(2)的条件下,作的平分线,交于点,求证:.
22.(12分)如图所示,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.
(1)当∠BDA=115°时,∠BAD= ;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”).
(2)当DC的长为多少时,△ABD与△DCE全等?请说明理由.
(3)在点D的运动过程中,△ADE的形状也在改变,请判断当∠BDA等于多少度时,△ADE是等腰三角形.(直接写出结论,不说明理由.)
23.(13分)如图,在等边△ABC中,AB=AC=BC=10厘米,DC=4厘米,如果点M以3厘米/秒的速度运动.
(1)如果点M在线段CB上由点C向点B运动,点N在线段BA上由B点向A点运动.它们同时出发,若点N的运动速度与点M的运动速度相等.经过2秒后,△BMN和△CDM是否全等?请说明理由;
(2)在(1)的条件下,当两点的运动时间为多少时,△BMN是一个直角三角形?
(3)若点N的运动速度与点M的运动速度不相等,点N从点B出发,点M以原来的运动速度从点C同时出发,都顺时针沿△ABC三边运动,经过25秒点M与点N第一次相遇,则点N的运动速度是多少厘米/秒.
人教版数学八年级上暑假预习课
第十七讲 轴对称自学检测卷(解析版)
一、专题导航
轴对称自学检测卷
考试范围:13章轴对称;考试时间:120分钟;满分120分
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 总分
得分
分卷I
评卷人 得分
. .
一、选择题(共10题;共30.0分)
1.(3分)剪纸又称刻纸,是中国最古老的民间艺术之一,它是以纸为加工对象,以剪刀(或刻刀)为工具进行创作的艺术.民间剪纸往往通过谐音、象征、寓意等手法提炼、概括自然形态,构成美丽的图案.下列剪纸中,既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
【答案】C
【解析】根据轴对称图形和中心对称图形的定义进行逐一判断即可.
解:A.原图是中心对称图形,不是轴对称图形,不符合题意;
B.原图是轴对称图形,不是中心对称图形,不符合题意;
C.原图既是中心对称图形,又是轴对称图形,符合题意;
D.原图是轴对称图形,不是中心对称图形,不符合题意;
故选:C.
2.(3分)如图,在△ABC中,AB=4,BC=7,DE是AC的中垂线,则△ABD的周长为( )
A. 10 B. 11 C. 12 D. 13
【答案】B
【解析】根据线段垂直平分线的性质得到DA=DC,再根据三角形的周长公式计算,得到答案.
解:∵DE是AC的中垂线,
∴DA=DC,
∴△ABD的周长=AB+BD+DA=AB+BD+DC=AB+BC,
∵AB=4,BC=7,
∴△ABD的周长=4+7=11,
故选:B.
3.(3分)如图,△ABC与△DEF关于直线MN成轴对称,则以下结论中不一定成立的是( )
A. AB=DE B. ∠B=∠E
C. AB∥DF D. 线段AD被MN垂直平分
【答案】C
【解析】根据轴对称的性质作答.
解:A、AB=DE,成立,不符合题意;
B、∠B=∠E,成立,不符合题意;
C、AB与DF不一定平行,不成立,符合题意;
D、线段AD被MN垂直平分,成立,不符合题意.
故选:C.
4.(3分)如图,两把相同的直尺的一边分别与射线OB、OA重合,另一边相交于点P,则OP平分∠BOA的依据是( )
A. 在角的内部,到角的两边距离相等的点在这个角的平分线上
B. 角平分线上的点到这个角的两边距离相等
C. 角平分线的性质
D. 角平分线是轴对称图形
【答案】A
【解析】过两把直尺的交点P作PE⊥AO,PF⊥BO,根据题意可得PE=PF,再根据角的内部到角的两边的距离相等的点在这个角的平分线上,可得OP平分∠AOB.
解:如图所示:PE⊥AO,过两把直尺的交点P作PF⊥BO,
∵两把完全相同的长方形直尺,
∴PE=PF,
∴OP平分∠AOB(角的内部到角的两边的距离相等的点在这个角的平分线上),
故选:A.
5.(3分)室内墙壁上挂一平面镜,小明在平面镜内看到他背后墙上时钟的示数如图所示,则这时的实际时间应是( )
A. 3:20 B. 3:40 C. 4:40 D. 8:20
【答案】B
【解析】根据镜面对称的性质,在平面镜中的像与现实中的事物恰好左右颠倒,且关于镜面对称,分析并作答.
解:根据镜面对称的性质,分析可得题中所显示的时刻与3:40成轴对称,所以此时实际时刻为3:40.
故选:B.
6.(3分)如图,中,是角平分线,垂足为,垂足为,与交于,下列说法不一定正确的是( )
A. 也是中线 B. 平分
C. D.
【答案】A
【解析】A.根据等腰三角形的三线合一可以判定A符合题意;
B.根据角平分线的性质得出,证明,得出,即可判断B不符合题意;
CD.根据全等三角形的性质得出,根据,证明垂直平分,即可判断CD不符合题意.
解:A.等腰三角形底边上的中线,顶角平分线,底边上的高线才三线合一,而不是等腰三角形,因此不一定是中线,故A符合题意;
B.∵是角平分线,,,
∴,
∵,
∴,
∴,
∴平分,故B不符合题意;
CD.∵,
∴,
∵,
∴垂直平分,
∴,,故CD不符合题意.
故选:A.
【点睛】本题主要考查了角平分线的性质,垂直平分线的判定,等腰三角形的性质,三角形全等的判定和性质,解题的关键是熟练掌握角平分线上的点到角的两边距离相等.
7.(3分)如图,在△ABC中,分别以点A和点C为圆心,大于的长为半径作弧(弧所在圆的半径都相等),两弧相交于M,N两点,直线MN分别与边BC,AC相交于点D,E,连接AD.若BD=DC,AE=4,AD=5,则AB的长为( )
A. 9 B. 8 C. 7 D. 6
【答案】D
【解析】根据线段垂直平分线的性质可得AC=2AE=8,DA=DC,从而可得∠DAC=∠C,再结合已知易得BD=AD,从而可得∠B=∠BAD,然后利用三角形内角和定理可得∠BAC=90°,从而在Rt△ABC中,利用勾股定理进行计算,即可解答.
解:由题意得:MN是AC的垂直平分线,
∴AC=2AE=8,DA=DC,
∴∠DAC=∠C,
∵BD=CD,
∴BD=AD,
∴∠B=∠BAD,
∵∠B+∠BAD+∠C+∠DAC=180°,
∴2∠BAD+2∠DAC=180°,
∴∠BAD+∠DAC=90°,
∴∠BAC=90°,
在Rt△ABC中,BC=BD+CD=2AD=10,
∴AB===6,
故选:D.
8.(3分)如图,等腰三角形ABC底边BC的长为4 cm,面积为12 cm2,腰AB的垂直平分线EF交AB于点E,交AC于点F,若D为BC边上的中点,M为线段EF上一点,则△BDM的周长最小值为( )
A. 5 cm B. 6 cm C. 8 cm D. 10 cm
【答案】C
【解析】连接AD,由于△ABC是等腰三角形,点D是BC边的中点,故AD⊥BC,再根据三角形的面积公式求出AD的长,再根据EF是线段AB的垂直平分线可知,点B关于直线EF的对称点为点A,故AD的长为BM+MD的最小值,由此即可得出结论.
如图,连接AD.
∵△ABC是等腰三角形,点D是BC边的中点,∴AD⊥BC,∴S△ABC=BC AD=×4×AD=12,解得:AD=6(cm).
∵EF是线段AB的垂直平分线,∴点B关于直线EF的对称点为点A,∴AD的长为BM+MD的最小值,∴△BDM的周长最短=(BM+MD)+BD=AD+BC=6+×4=6+2=8(cm).
故选C.
【点睛】本题考查的是轴对称﹣最短路线问题,熟知等腰三角形三线合一的性质是解答此题的关键.
9.(3分)如图,在△ABC中,∠C=90°,BC=8、AC=6,若点P为直线BC上一点,且△ABP为等腰三角形,则符合条件的点P有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】依据点P为直线BC上一点,且△ABP为等腰三角形,需要分三种情况进行讨论,即①AB=AP,②BA=BP,③AP=BP,据此通过画图即可得出点P的位置.
解:如图所示,分别以A,B为圆心,AB的长为半径画弧,与直线l的交点P1,P2,P3即为所求;作AB的垂直平分线,与直线l的交点P4即为所求.
∴符合条件的点P有4个.
故选:D.
10.(3分)如图,在△ABC中,∠BAC和∠ABC的平分线AE,BF相交于点O,AE交BC于E,BF交AC于F,过点O作OD⊥BC于D,下列三个结论:①∠AOB=90°+∠C;②当∠C=60°时,AF+BE=AB;③若OD=a,AB+BC+CA=2b,则S△ABC=ab.其中正确的是( )
A. ①② B. ②③ C. ①②③ D. ①③
【答案】C
【解析】由角平分线的定义结合三角形的内角和的可求解∠AOB与∠C的关系,进而判定①;在AB上取一点H,使BH=BE,证得△HBO≌△EBO,得到∠BOH=∠BOE=60°,再证得△HAO≌△FAO,得到AF=AH,进而判定②正确;作OH⊥AC于H,OM⊥AB于M,根据三角形的面积可证得③正确.
解:∵∠BAC和∠ABC的平分线相交于点O,
∴∠OBA=∠CBA,∠OAB=∠CAB,
∴∠AOB=180°-∠OBA-∠OAB=180°-∠CBA-∠CAB=180°-(180°-∠C)=90°+∠C,①正确;
∵∠C=60°,
∴∠BAC+∠ABC=120°,
∵AE,BF分别是∠BAC与ABC的平分线,
∴∠OAB+∠OBA=(∠BAC+∠ABC)=60°,
∴∠AOB=120°,
∴∠AOF=60°,
∴∠BOE=60°,
如图,在AB上取一点H,使BH=BE,
∵BF是∠ABC的角平分线,
∴∠HBO=∠EBO,
在△HBO和△EBO中,,
∴△HBO≌△EBO(SAS),
∴∠BOH=∠BOE=60°,
∴∠AOH=180°-60°-60°=60°,
∴∠AOH=∠AOF,
在△HAO和△FAO中,,
∴△HAO≌△FAO(ASA),
∴AF=AH,
∴AB=BH+AH=BE+AF,故②正确;
作OH⊥AC于H,OM⊥AB于M,
∵∠BAC和∠ABC的平分线相交于点O,
∴点O在∠C的平分线上,
∴OH=OM=OD=a,
∵AB+AC+BC=2b
∴S△ABC=×AB×OM+×AC×OH+×BC×OD=(AB+AC+BC) a=ab,③正确.
故选:C.
分卷II
评卷人 得分
. .
二、填空题(共5题;共15.0分)
11.(3分)如图,△AOB与△COB关于边OB所在的直线成轴对称,AO的延长线交BC于点D.若∠BOD=45°,∠C=20°,则∠ADC=_____.
【答案】70°
【解析】根据对称性得出∠BOC=∠AOB=180°-∠BOD=135°,∠COD=∠BOC-∠BOD=135°-45°=90°,根据三角形内角和得出结论即可.
解:∵△AOB与△COB关于边OB所在的直线成轴对称,
∴∠BOC=∠AOB=180°-∠BOD=135°,∠COD=∠BOC-∠BOD=135°-45°=90°,
∴∠ADC=180°-∠C-∠COD=180°-20°-90°=70°,
故答案为:70°.
12.(3分)如图,课间休息时,小新将镜子放在桌面上,无意间看到镜子中有一串数字,原来是桌旁墙面上张贴的同学手机号码中的几个数字,请问镜子中的数字对应的实际数字是_____.
【答案】630085
【解析】易得所求的数字与看到的数字关于竖直的一条直线成轴对称,作出相应图形即可求解.
解:做轴对称图形得:|630085,
故答案是:630085.
13.(3分)如图,在中,,是的平分线,.若P,Q分别是和上的动点,则的最小值是_____.
【答案】
【解析】根据等腰三角形三线合一的性质得出,过点B作于点Q,交于点P,则此时取最小值,最小值为的长,然后利用三角形等面积法求解即可.
解:∵,是的平分线,
∴垂直平分,
∴.
过点B作于点Q,交于点P,则此时取最小值,最小值为的长,如图所示.
∵,
∴=,
即的最小值是.
故答案为:.
【点睛】题目主要考查等腰三角形的性质及三角形等面积法,最短距离问题,理解题意,熟练掌握等腰三角形的性质是解题关键.
14.(3分)如图,在等边三角形ABC中,AB=2,BD是AC边上的高,延长BC至点E,使CE=CD,则BE的长为_______.
【答案】3
【解析】由等边三角形的性质可得AC=BC=AB=2,根据BD是AC边上的高,可得AD=CD=1,再由题中条件CE=CD,即可求得BE.
解:∵△ABC是等边三角形,
∴AC=BC=AB=2,
∵BD是AC边上的高,
∴D为AC的中点,
∴AD=CD=AC=1,
∴CE=CD=1,
∴BE=BC+CE=2+1=3.
故答案为:3.
【点睛】本题考查了等边三角形的性质,等腰三角形的性质,考查了学生综合运用数学知识的能力,得到AD=CD=AC是正确解答本题的关键.
15.(3分)如图,∠AOB=120°,点P为∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:①PM=PN;②OM+ON=OP;③四边形PMON的面积保持不变;④△PMN的周长保持不变.其中说法正确的是_______.(填序号)
【答案】①②③
【解析】作PE⊥OA于E,PF⊥OB于F,根据题意得:∠EPM=∠FPN,再根据角平分线的性质定理可得PE=PF,从而得到Rt△POE≌Rt△POF,进而得到OE=OF,可得到△PEM≌△PFN,从而得到∠PEM=∠PFN,EM=NF,PM=PN,可得S△PEM=S△PFN,OM+ON= 2OE,从而得到①②③正确,再由M,N的位置变化,可得MN的长度是变化的,再证得△PMN是等边三角形,可得故④错误,即可求解.
解:如图,作PE⊥OA于E,PF⊥OB于F,
∵∠PEO=∠PFO=90°,
∴∠EPF+∠AOB=180°,
∵∠MPN+∠AOB=180°,
∴∠EPF=∠MPN,
∴∠EPM=∠FPN,
∵OP平分∠AOB,PE⊥OA,PF⊥OB,
∴PE=PF,
在Rt△POE和Rt△POF中,
∵OP=OP,PE=PF,
∴Rt△POE≌Rt△POF(HL),
∴OE=OF,
在△PEM和△PFN中,
∵∠MPE=∠NPF, PE=PF,∠PEM=∠PFN,
∴△PEM≌△PFN(ASA),
∴∠PEM=∠PFN,EM=NF,PM=PN,故①正确;
∴S△PEM=S△PFN,
∴S四边形PMON=S四边形PEOF=定值,故③正确;
∵OM+ON=OE+ME+OF-NF=2OE=定值,故②正确;
∵M,N的位置变化,
∴MN的长度是变化的,
∵PM=PN,∠MPN=60°,
∴△PMN是等边三角形,
∴△PMN的周长是变化的,故④错误,
∴说法正确的有①②③.
故答案为:①②③
【点睛】本题主要考查了全等三角形的判定和性质,角平分线的性质定理,等边三角形判定和性质等知识,熟练掌握全等三角形的判定和性质,角平分线的性质定理,等边三角形判定和性质等知识是解题的关键.
评卷人 得分
. .
三、解答题(共8题;共75.0分)
16.(8分)如图,在△ABC中,∠ABC=70°,AB=AC=8,D为BC中点,点N在线段AD上,NM∥AC交AB于点M,BN=3.
(1)求∠CAD度数;
(2)求△BMN的周长.
【解析】(1)由等腰三角形性质和三角形内角和定理可求出∠CAD度数;
(2)由平行线的性质及等腰三角形性质可得到AM=NM,则求△BMN的周长可转化成求线段AB和线段BN的和,由题中给出的条件即可求出结果.
解:(1)∵AB=AC,
∴△ABC是等腰三角形,
又∵∠ABC=70°,
∴∠BAC=180°-70°×2=40°,
又∵D为BC的中点,
∴AD平分∠BAC,
∴∠CAD=∠BAD=∠BAC=×40°=20°,
故∠CAD度数为20°.
(2)∵NM∥AC,
∴∠ANM=∠CAD,
又∵∠CAD=∠BAD,
∴∠ANM=∠BAD,
∴AM=NM,
∴△BMN的周长=MB+BN+NM=AB+BN,
∵AB=8,BN=3,
∴△BMN的周长=8+3=11.
故△BMN的周长为11.
17.(8分)如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(-3,1),B(2,3),C(1,0).
(1)在图中作△A'B'C',使得△A'B'C'与△ABC关于直线l轴对称.
(2)点A'的坐标为 _____,点B'的坐标为 _____.
【答案】(1)(-3,-3);(2)(2,-5);
【解析】(1)根据轴对称的性质作图即可.
(2)由图可得答案.
解:(1)如图,△A'B'C'即为所求.
(2)由图可得,A'(-3,-3),B'(2,-5).
故答案为:(-3,-3);(2,-5).
18.(6分)已知:如图,在等腰△ABC中,AB=AC.求作:在BC边上找一点D,使得AD=CD.
小李同学在学习了尺规作图的相关知识后,设计作图步骤如下:
①分别以点A,C为圆心,大于AC长为半径作弧,两弧相交于M,N两点;
②连接MN,交BC于点D,连接AD;
③点D即为所求.
(1)请根据上述的设计方案,补全作图痕迹,并分析小李同学的作图依据是 _____;
(2)补充下面的证明过程:
证明:设MN交AC于点E,
∵MN垂直平分AC,
∴∠AED=∠CED=90°,_____,DE=DE,
∴△AED≌△CED,
∴AD=_____.( _____)(填推理依据).
【答案】(1)线段垂直平分线上的点到线段两端点的距离相等;(2)垂直的定义;(3)CD;(4)线段垂直平分线上的点到线段两端点的距离相等;
【解析】(1)根据线段垂直平分线的性质作出图形即可;
(2)根据线段垂直平分线的性质即可得到结论.
解:(1)如图所示,
作图依据是线段垂直平分线上的点到线段两端点的距离相等;
故答案为:线段垂直平分线上的点到线段两端点的距离相等;
(2)证明:设MN交AC于点E,
∵MN垂直平分AC,
∴∠AED=∠CED=90°,(垂直的定义)DE=DE,
∴△AED≌△CED,
∴AD=CD.( 线段垂直平分线上的点到线段两端点的距离相等)(填推理依据).
故答案为:垂直的定义,CD,线段垂直平分线上的点到线段两端点的距离相等.
19.(9分)如图,在中,垂直平分,分别交,于点、,垂直平分,分别交、于点、,连接,.
(1)若,求的周长等于__________.
(2)若,求的度数
【答案】(1)9 (2)见解析
【解析】(1)根据垂直平分线的性质得出,,根据三角形周长公式即可求解;
(2)根据三角形内角和定理求得,根据垂直平分线的性质以及等边对等角可得, ,进而根据三角形内角和定理即可求解.
【小问1详解】
解:∵是的垂直平分线,
∴,
∵是的垂直平分线,
∴,
∴的周长为.
【小问2详解】
解:∵,
∴,
∵是的垂直平分线,
∴,
∴,
同理可得:,
∴,
∴.
【点睛】本题考查了垂直平分线的性质,等边对等角,三角形内角和定理,掌握以上知识是解题的关键.
20.(9分)阅读下面材料,并解决相应的问题:
在数学课上,老师给出如下问题,已知线段AB,求作线段AB的垂直平分线.小明的作法如下:
(1)分别以A,B为圆心,大于AB长为半径作弧,两弧交于点C;
(2)再分别以A,B为圆心,大于AB长为半径作弧,两弧交于点D;
(3)作直线CD,直线CD即为所求的垂直平分线.
同学们对小明的作法提出质疑,小明给出了这个作法的证明如下:
连接AC,BC,AD,BD.
由作图可知:AC=BC,AD=BD.
∴点C,点D在线段的垂直平分线上(依据1:_____).
∴直线就是线段的垂直平分线(依据2:_____).
(1)请你将小明证明的依据写在横线上;
(2)将小明所作图形放在如图的正方形网格中,点A,B,C,D恰好均在格点上,依次连接A,C,B,D,A各点,得到如图所示的“箭头状”的基本图形,请在网格中添加若干个此基本图形,使其各顶点也均在格点上,且与原图形组成的新图形是中心对称图形.
【答案】(1)到线段两个端点距离相等的点在这条线段的垂直平分线上;(2)两点确定一条直线;
【解析】(1)根据线段的垂直平分线的判定和性质判断即可.
(2)作点C,D关于AB的对称点C′,D′,连接AC′,BC′,AD′,BD′即可.
解:(1)连接AC,CB,AD,DB.
由作图可知:AC=BC,AD=BD.
∴点C,点D在线段的垂直平分线上(到线段两个端点距离相等的点在这条线段的垂直平分线上).
∴直线就是线段的垂直平分线(两点确定一条直线).
故答案为:线段的垂直平分线的性质,两点确定一条直线.
(2)如图所示:
21.(10分)如图,.
(1)写出与的数量关系
(2)延长到,使,延长到,使,连接.求证:.
(3)在(2)的条件下,作的平分线,交于点,求证:.
【答案】(1),
(2)见解析 (3)见解析
【解析】(1)勾股定理求得,结合已知条件即可求解;
(2)根据题意画出图形,证明,得出,则,即可得证;
(3)延长交于点,延长交于点,根据角平分线以及平行线的性质证明,进而证明,即可得证.
【小问1详解】
解:∵
∴,
∵
∴
即;
【小问2详解】
证明:如图所示,
∴
∴,
∵,
∴
∵,,
∴
∴
∴
∴
【小问3详解】
证明:如图所示,延长交于点,延长交于点,
∵,,
∴,
∴
∵是的角平分线,
∴,
∴
∴
∵,
∴,,
∴,
又∵,
∴,
即,
∴,
又,则,
在中,
,
∴,
∴
【点睛】本题考查了全等三角形的性质与判定,等腰三角形的性质与判定,勾股定理,平行线的性质与判定,熟练掌握全等三角形的性质与判定是解题的关键.
22.(12分)如图所示,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.
(1)当∠BDA=115°时,∠BAD= ;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”).
(2)当DC的长为多少时,△ABD与△DCE全等?请说明理由.
(3)在点D的运动过程中,△ADE的形状也在改变,请判断当∠BDA等于多少度时,△ADE是等腰三角形.(直接写出结论,不说明理由.)
【答案】(1)25°;小;
(2)DC=2,理由见解答过程;
(3)110°或80°.
【解析】(1)根据三角形内角和定理计算求出∠BAD,根据点D从点B向点C运动可以得出∠BDA逐渐变小;
(2)当DC=2时,AB=DC,根据∠DEC+∠EDC=140°,∠ADB+∠EDC=140°,得到∠ADB=∠DEC,利用AAS定理证明△ABD≌△DCE即可;
(3)分DA=DE、AE=AD、EA=ED三种情况,根据等腰三角形的性质、三角形内角和定理计算.
【小问1详解】
解:∵∠B=40°,∠BDA=115°,
∴∠BAD=180°-∠B-∠BDA=180°-115°-40°=25°,
由图形可知,∠BDA逐渐变小,
故答案为:25°;小;
【小问2详解】
当DC=2时,△ABD≌△DCE,
理由如下:∵AB=2,
∴AB=DC,
∵AB=AC,
∴∠C=∠B=40°,
∴∠DEC+∠EDC=140°,
∵∠ADE=40°,
∴∠ADB+∠EDC=140°,
∴∠ADB=∠DEC,
在△ABD和△DCE中,
∴△ABD≌△DCE(AAS);
【小问3详解】
当∠BDA的度数为110°或80°时,△ADE是等腰三角形,理由如下:
当DA=DE时,∠DAE=∠DEA=70°,
∴∠BDA=∠DAE+∠C=70°+40°=110°;
当AD=AE时,∠AED=∠ADE=40°,
∴∠DAE=100°,
此时,点D与点B重合,不合题意;
当EA=ED时,∠EAD=∠ADE=40°,
∴∠BDA=∠DAE+∠C=40°+40°=80°,
综上所述,当∠BDA的度数为110°或80°时,△ADE是等腰三角形.
【点睛】本题考查的是等腰三角形的判定与性质、全等三角形的判定与性质、三角形外角的性质,掌握全等三角形的判定定理和性质定理、灵活运用分情况讨论思想是解题的关键.
23.(13分)如图,在等边△ABC中,AB=AC=BC=10厘米,DC=4厘米,如果点M以3厘米/秒的速度运动.
(1)如果点M在线段CB上由点C向点B运动,点N在线段BA上由B点向A点运动.它们同时出发,若点N的运动速度与点M的运动速度相等.经过2秒后,△BMN和△CDM是否全等?请说明理由;
(2)在(1)的条件下,当两点的运动时间为多少时,△BMN是一个直角三角形?
(3)若点N的运动速度与点M的运动速度不相等,点N从点B出发,点M以原来的运动速度从点C同时出发,都顺时针沿△ABC三边运动,经过25秒点M与点N第一次相遇,则点N的运动速度是多少厘米/秒.
【解析】(1)由题意得到BM,BN,CM的长度,利用边角边公理即可判定结论;
(2分两种情形讨论解答:①当∠BNM=90°时;②当∠BMN=90°时,设两点的运动时为t秒,分别表示出BM,BN的长度,所对的直角边等于斜边的一半列出方程即可求出对应的时间;
(3)分两种情况解答:①当点N的速度小于点M的速度时;②当点N的速度大于点M的速度时,设点N速度为s厘米/秒,利用点M与点N第一次相遇时的路程的差列出方程即可求解.
解:(1)△BMN和△CDM全等.理由:
∵点N的运动速度与点M的运动速度相等,点M以3厘米/秒的速度运动,
∴点N的速度是3厘米/秒.
∴经过2秒后,CM=6厘米,BN=6厘米,
∴CM=BN,
∴BM=BC-CM=10-6=4(厘米).
∵DC=4厘米,
∴BM=CD.
∵AB=AC=BC,
∴∠B=∠C=60°.
在△BMN和△CDM中,
,
∴△BMN△CDM(SAS).
(2)设两点的运动时为t秒,则CM=BN=3t厘米,
∴BM=BC-CM=(10-3t)厘米.
①当∠BNM=90°时,
∵∠B=60°,
∴∠BMN=30°.
∴BN=BM.
∴3t=(10-3t).
解得:t=.
②当∠BMN=90°时,
∵∠B=60°,
∴∠BMN=30°.
∴BM=BN,
∴10-3t=×3t.
解得:t=.
综上,当两点的运动时间为秒或秒时,△BMN是一个直角三角形.
(3)设点N速度为s厘米/秒,则点N25秒运动的距离为25s厘米,
①当点N的速度小于点M的速度时,由题意得:
25×3-25s=10,
解得:s=.
②当点N的速度大于点M的速度时,由题意得:
25s-25×3=20.
解得:s=.
综上,经过25秒点M与点N第一次相遇,则点N的运动速度是厘米/秒或米/秒.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
