人教版高中数学(2019)选择性必修一第二章2.1.1倾斜角与斜率 课件(共17张PPT)
文档属性
| 名称 | 人教版高中数学(2019)选择性必修一第二章2.1.1倾斜角与斜率 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-29 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
2.1.1 倾斜角与斜率
y
o
x
P
l
.
Q
1、直线的倾斜角
1.直线倾斜角的定义
*注意:(1)x轴的正方向。
(2)直线 向上方向(x轴上方);
当直线 l 与x轴相交时,我们以x轴为基准,x轴正方向与直线l 向上的方向之间所成的角α叫做直线l 的倾斜角.
练习:下列图中标出的直线的倾斜角对不对?如果不对,违背了定义中的哪一条?
x
y
o
x
y
o
x
y
o
x
y
o
(1)
(2)
(3)
(4)
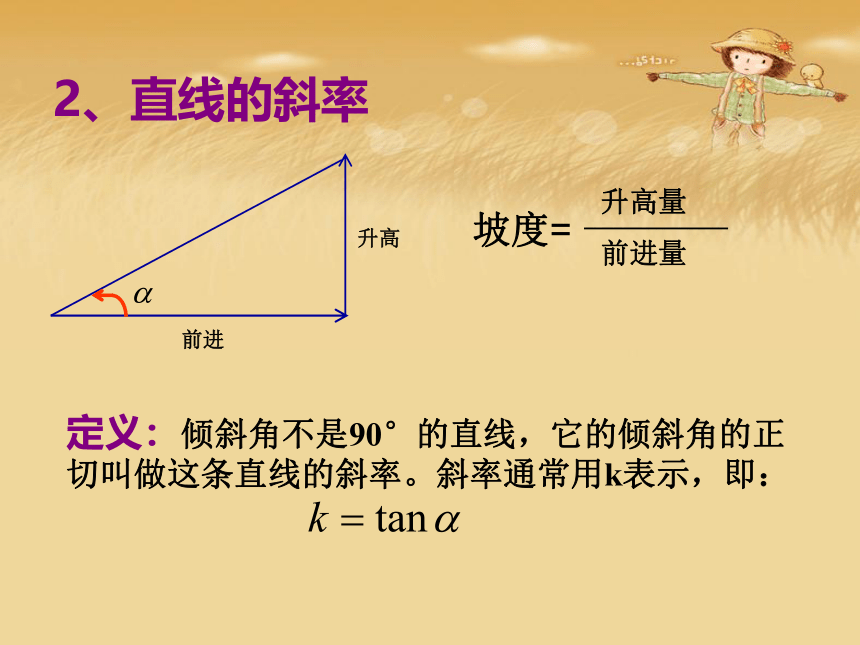
2、直线的斜率
升高
前进
定义:倾斜角不是90°的直线,它的倾斜角的正切叫做这条直线的斜率。斜率通常用k表示,即:
坡度=
升高量
前进量
定义:倾斜角不是90°的直线,它的倾斜角的正切叫做这条直线的斜率。斜率通常用k表示,即:
2、直线的斜率
倾斜角是90 °的直线没有斜率。
描述直线倾斜程度的量——直线的斜率
应用:
O
x
y
例1:如图,直线 的倾斜角 =300,直线l2⊥l1,求l1,l2 的斜率。
解:
例4 直线 l1、 l2、 l3的斜率分别是k1、 k2、 k3,试比较斜率的大小
l1
l2
l3
p
o
y
x
y
p
o
x
p
o
y
x
p
o
y
x
0°< < 90°
= 90°
90°< <180°
= 0°
k=0
k >0
k不存在
k<0
x
y
O
P1(x1,y1)
P2(x2,y2)
α
α
已知直线上两点:P1(x1,y1),P2(x2,y2),
如何求斜率k?
3、斜率公式
x
y
O
Q (x2,y1)
P2(x2,y2)
P1(x1,y1)
Q (x2,y1)
P2(x2,y2)
P1(x1,y1)
P2(x2,y2)
P1(x1,y1)
如何用两点的坐标表示直线的斜率
直线的斜率计算公式:
例2:求过A(-2,0),B(-5,3)两点的
直线的斜率和倾斜角
变式1: A(-5,0),B(-5,3)
变式2: A(-2,1),B(-5,3)
例3 判断正误:
②直线的斜率为 ,则它的倾斜角为 ( )
③因为所有直线都有倾斜角,所以所有直线都有
斜率。 ( )
①直线的倾斜角为α,则直线的斜率为 ( )
④因为平行于y轴的直线的斜率不存在,所以平
行于y轴的直线的倾斜角不存在 ( )
⑤直线的倾斜角越大,则直线的斜率越大 ( )
小结:
直线的倾斜角 斜率 斜率公式
定义
范围
三要素
学以致用:
学以致用:
2.1.1 倾斜角与斜率
y
o
x
P
l
.
Q
1、直线的倾斜角
1.直线倾斜角的定义
*注意:(1)x轴的正方向。
(2)直线 向上方向(x轴上方);
当直线 l 与x轴相交时,我们以x轴为基准,x轴正方向与直线l 向上的方向之间所成的角α叫做直线l 的倾斜角.
练习:下列图中标出的直线的倾斜角对不对?如果不对,违背了定义中的哪一条?
x
y
o
x
y
o
x
y
o
x
y
o
(1)
(2)
(3)
(4)
2、直线的斜率
升高
前进
定义:倾斜角不是90°的直线,它的倾斜角的正切叫做这条直线的斜率。斜率通常用k表示,即:
坡度=
升高量
前进量
定义:倾斜角不是90°的直线,它的倾斜角的正切叫做这条直线的斜率。斜率通常用k表示,即:
2、直线的斜率
倾斜角是90 °的直线没有斜率。
描述直线倾斜程度的量——直线的斜率
应用:
O
x
y
例1:如图,直线 的倾斜角 =300,直线l2⊥l1,求l1,l2 的斜率。
解:
例4 直线 l1、 l2、 l3的斜率分别是k1、 k2、 k3,试比较斜率的大小
l1
l2
l3
p
o
y
x
y
p
o
x
p
o
y
x
p
o
y
x
0°< < 90°
= 90°
90°< <180°
= 0°
k=0
k >0
k不存在
k<0
x
y
O
P1(x1,y1)
P2(x2,y2)
α
α
已知直线上两点:P1(x1,y1),P2(x2,y2),
如何求斜率k?
3、斜率公式
x
y
O
Q (x2,y1)
P2(x2,y2)
P1(x1,y1)
Q (x2,y1)
P2(x2,y2)
P1(x1,y1)
P2(x2,y2)
P1(x1,y1)
如何用两点的坐标表示直线的斜率
直线的斜率计算公式:
例2:求过A(-2,0),B(-5,3)两点的
直线的斜率和倾斜角
变式1: A(-5,0),B(-5,3)
变式2: A(-2,1),B(-5,3)
例3 判断正误:
②直线的斜率为 ,则它的倾斜角为 ( )
③因为所有直线都有倾斜角,所以所有直线都有
斜率。 ( )
①直线的倾斜角为α,则直线的斜率为 ( )
④因为平行于y轴的直线的斜率不存在,所以平
行于y轴的直线的倾斜角不存在 ( )
⑤直线的倾斜角越大,则直线的斜率越大 ( )
小结:
直线的倾斜角 斜率 斜率公式
定义
范围
三要素
学以致用:
学以致用:
