北师大版数学六年级下册 一 圆柱与圆锥复习课件(共21张PPT)
文档属性
| 名称 | 北师大版数学六年级下册 一 圆柱与圆锥复习课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-29 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
第一单元知识点巩固
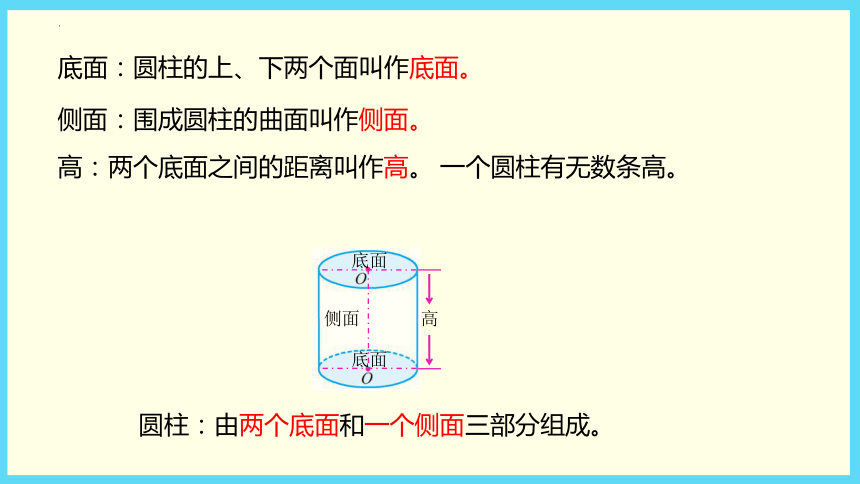
底面:圆柱的上、下两个面叫作底面。
侧面:围成圆柱的曲面叫作侧面。
高:两个底面之间的距离叫作高。 一个圆柱有无数条高。
底面
底面
侧面
高
圆柱:由两个底面和一个侧面三部分组成。
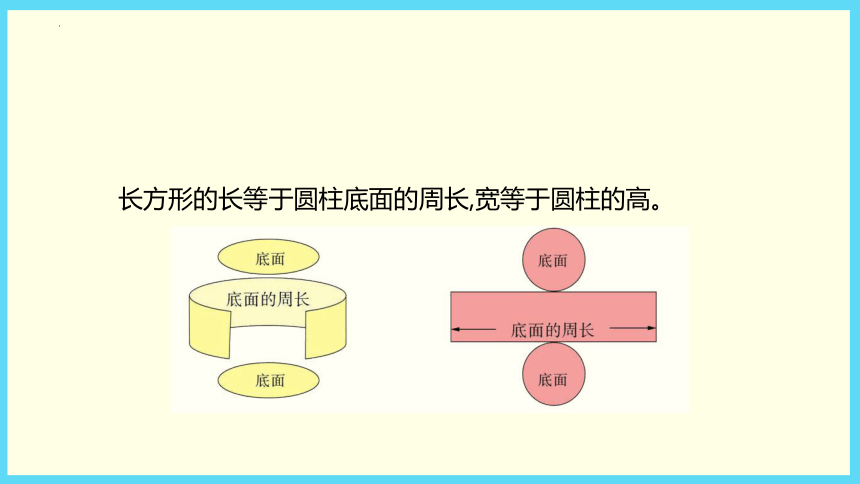
长方形的长等于圆柱底面的周长,宽等于圆柱的高。
顶点
侧面
高
顶点:圆锥有一个顶点。
底面:圆锥的底面是一个圆。
侧面:圆锥的侧面是曲面。
o
底面
高:从圆锥的顶点到底面圆心的距离是圆锥的高。圆锥只有一条高。
圆锥:由一个底面和一个侧面两部分组成。
圆锥的底面是一个圆,侧面是曲面。
圆锥的侧面展开图是一个扇形。(如下图所示)
填一填
(1)圆柱上下面是两个( )的圆形,圆锥的底面是一个( )形。
(2)圆柱有( )个面是弯曲的,圆柱的侧面沿着一条高展开后是一个( )。
(3)圆柱两个底面之间的距离叫圆柱的( ),一个圆柱有( )条高。
(4)从圆锥的( )到( )的距离是圆锥的高,一个圆锥只有( )条高。
相等
圆
一
长方形或正方形
高
无数
顶点
底面圆心
一
所以,圆柱的侧面积 = 底面周长 × 高
长方形的长
圆柱的底面周长
长方形的宽
圆柱的高
因为,长方形的面积 = 长 × 宽
如果用S侧表示圆柱的侧面积,C 表示底面周长,h 表示高,那么圆柱侧面积的字母公式是S侧=Ch。
1、已知圆柱底面直径、圆柱的高,求圆柱的侧面积
2、已知圆柱底面半径、圆柱的侧面积,求圆柱的高
3、已知圆柱的侧面积、圆柱的高,求圆柱底面直径
d=4cm h=6cm
r=4cm C=9.42
h=4cm C=9.42
怎样计算这个圆柱的表面积?先想一想,再计算。
圆柱的表面积
=
圆柱的侧面积
+
圆柱的两个底面积
S表
S侧
2S底
=
+
S表
Ch
2πr2
=
+
慧眼识真
1.给一个圆柱形的柱子刷油漆,求刷油漆的面积,就是求这个圆柱的( )。
A.侧面积 B.底面积 C.表面积
A
2.做一个圆柱形的木桶至少需要木板多少平方分米,就是求这个圆柱的( )。
A.表面积 B.底面积 C.侧面积+一个底面积
C
3.求广场上一根花柱的占地面积,就是求它的( )。
A.侧面积 B.底面积 C.表面积
B
1、已知圆柱底面直径、圆柱的高,求圆柱的表面积
2、已知圆柱底面半径、圆柱的侧面积,求圆柱的表面积
3、已知圆柱的侧面积、圆柱的高,求圆柱的表面积。
把圆柱的底面平均分成16份,切开后照下图的样子拼一拼。
拼成了一个近似的长方体。
分成的份数越多,就越接近长方体。
长方体的体积
底面积
底面积
高
高
=
×
=
×
=πr h
如果用V 表示圆柱的体积,S 表示圆柱的底面积, h 表示圆柱的高,圆柱的体积公式可以写成: V = Sh
圆柱的体积
想一想、填一填:
把圆柱体切割拼成近似( ),它们的( )相等。长方体的高就是圆柱体的( ),长方体的底面积就是圆柱体的( ),因为长方体的体积=( ),所以圆柱体的体积=( )。用字母“V”表示( ),“S”表示( ),“h”表示( ),那么,圆柱体体积用字母表示为( )
长方体
体积
高
底面积
底面积×高
底面积×高
体积
底面积
高
V=Sh
1、已知圆柱底面直径、圆柱的高,求圆柱的体积
2、已知圆柱底面半径、圆柱的侧面积,求圆柱的体积
3、已知圆柱的侧面积、圆柱的高,求圆柱的体积。
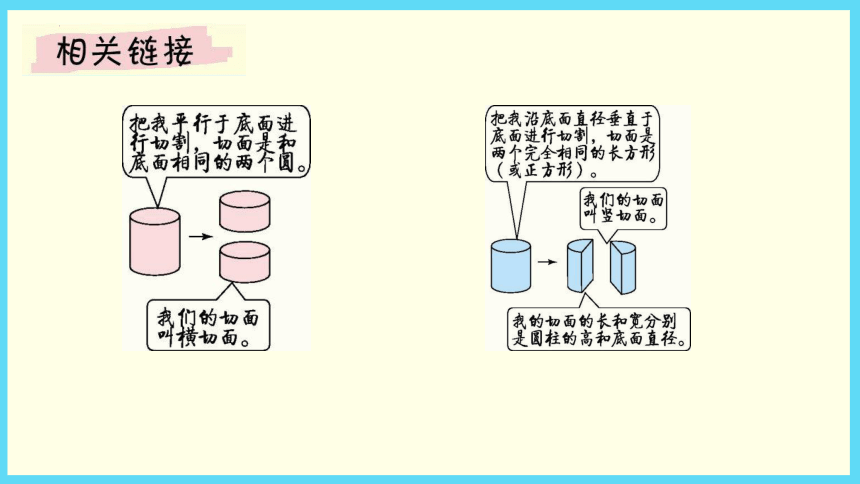
1、圆柱的两种切法增加面积的相关问题
2、圆柱的高增加和减少,表面积变化相关问题
r=2cm
h=4cm
r=2cm
h=4cm
一个高为10厘米的圆柱,如果它的高减少3厘米,表面积就减少37.68平方米,求原来圆柱的体积
圆柱体积=底面积 X 高
等底等高的圆锥体积是圆柱体积的
1
3
圆锥的体积=底面积×高 ×
1
3
1.一个圆锥与一个圆柱等底等高,
已知圆锥的体积是 8 立方米,
圆柱的体积是( )。
2.一个圆锥与一个圆柱等底等体积,
已知圆柱的高是 2 厘米, 圆锥的
高是( )。
3.一个圆锥与一个圆柱等高等体积,
已知圆柱的底面积是 6平方米,
圆锥的底面积是( )。
24立方米
6 厘米
18平方米
144÷(3+1)
36×3=108
36
108
4.一个圆柱与和它等底等高的圆锥的体积和是144立方厘米。圆柱的体积是( )立方厘米,圆锥的体积是( )立方厘米。
5.一个圆柱体比它等底等高的圆锥体积大48立方厘米,圆柱体积是( )立方厘米,圆锥体积是( )立方厘米。
48÷(3-1)
24
24×3=72
72
再
见
第一单元知识点巩固
底面:圆柱的上、下两个面叫作底面。
侧面:围成圆柱的曲面叫作侧面。
高:两个底面之间的距离叫作高。 一个圆柱有无数条高。
底面
底面
侧面
高
圆柱:由两个底面和一个侧面三部分组成。
长方形的长等于圆柱底面的周长,宽等于圆柱的高。
顶点
侧面
高
顶点:圆锥有一个顶点。
底面:圆锥的底面是一个圆。
侧面:圆锥的侧面是曲面。
o
底面
高:从圆锥的顶点到底面圆心的距离是圆锥的高。圆锥只有一条高。
圆锥:由一个底面和一个侧面两部分组成。
圆锥的底面是一个圆,侧面是曲面。
圆锥的侧面展开图是一个扇形。(如下图所示)
填一填
(1)圆柱上下面是两个( )的圆形,圆锥的底面是一个( )形。
(2)圆柱有( )个面是弯曲的,圆柱的侧面沿着一条高展开后是一个( )。
(3)圆柱两个底面之间的距离叫圆柱的( ),一个圆柱有( )条高。
(4)从圆锥的( )到( )的距离是圆锥的高,一个圆锥只有( )条高。
相等
圆
一
长方形或正方形
高
无数
顶点
底面圆心
一
所以,圆柱的侧面积 = 底面周长 × 高
长方形的长
圆柱的底面周长
长方形的宽
圆柱的高
因为,长方形的面积 = 长 × 宽
如果用S侧表示圆柱的侧面积,C 表示底面周长,h 表示高,那么圆柱侧面积的字母公式是S侧=Ch。
1、已知圆柱底面直径、圆柱的高,求圆柱的侧面积
2、已知圆柱底面半径、圆柱的侧面积,求圆柱的高
3、已知圆柱的侧面积、圆柱的高,求圆柱底面直径
d=4cm h=6cm
r=4cm C=9.42
h=4cm C=9.42
怎样计算这个圆柱的表面积?先想一想,再计算。
圆柱的表面积
=
圆柱的侧面积
+
圆柱的两个底面积
S表
S侧
2S底
=
+
S表
Ch
2πr2
=
+
慧眼识真
1.给一个圆柱形的柱子刷油漆,求刷油漆的面积,就是求这个圆柱的( )。
A.侧面积 B.底面积 C.表面积
A
2.做一个圆柱形的木桶至少需要木板多少平方分米,就是求这个圆柱的( )。
A.表面积 B.底面积 C.侧面积+一个底面积
C
3.求广场上一根花柱的占地面积,就是求它的( )。
A.侧面积 B.底面积 C.表面积
B
1、已知圆柱底面直径、圆柱的高,求圆柱的表面积
2、已知圆柱底面半径、圆柱的侧面积,求圆柱的表面积
3、已知圆柱的侧面积、圆柱的高,求圆柱的表面积。
把圆柱的底面平均分成16份,切开后照下图的样子拼一拼。
拼成了一个近似的长方体。
分成的份数越多,就越接近长方体。
长方体的体积
底面积
底面积
高
高
=
×
=
×
=πr h
如果用V 表示圆柱的体积,S 表示圆柱的底面积, h 表示圆柱的高,圆柱的体积公式可以写成: V = Sh
圆柱的体积
想一想、填一填:
把圆柱体切割拼成近似( ),它们的( )相等。长方体的高就是圆柱体的( ),长方体的底面积就是圆柱体的( ),因为长方体的体积=( ),所以圆柱体的体积=( )。用字母“V”表示( ),“S”表示( ),“h”表示( ),那么,圆柱体体积用字母表示为( )
长方体
体积
高
底面积
底面积×高
底面积×高
体积
底面积
高
V=Sh
1、已知圆柱底面直径、圆柱的高,求圆柱的体积
2、已知圆柱底面半径、圆柱的侧面积,求圆柱的体积
3、已知圆柱的侧面积、圆柱的高,求圆柱的体积。
1、圆柱的两种切法增加面积的相关问题
2、圆柱的高增加和减少,表面积变化相关问题
r=2cm
h=4cm
r=2cm
h=4cm
一个高为10厘米的圆柱,如果它的高减少3厘米,表面积就减少37.68平方米,求原来圆柱的体积
圆柱体积=底面积 X 高
等底等高的圆锥体积是圆柱体积的
1
3
圆锥的体积=底面积×高 ×
1
3
1.一个圆锥与一个圆柱等底等高,
已知圆锥的体积是 8 立方米,
圆柱的体积是( )。
2.一个圆锥与一个圆柱等底等体积,
已知圆柱的高是 2 厘米, 圆锥的
高是( )。
3.一个圆锥与一个圆柱等高等体积,
已知圆柱的底面积是 6平方米,
圆锥的底面积是( )。
24立方米
6 厘米
18平方米
144÷(3+1)
36×3=108
36
108
4.一个圆柱与和它等底等高的圆锥的体积和是144立方厘米。圆柱的体积是( )立方厘米,圆锥的体积是( )立方厘米。
5.一个圆柱体比它等底等高的圆锥体积大48立方厘米,圆柱体积是( )立方厘米,圆锥体积是( )立方厘米。
48÷(3-1)
24
24×3=72
72
再
见
