直线与圆的位置关系（3）

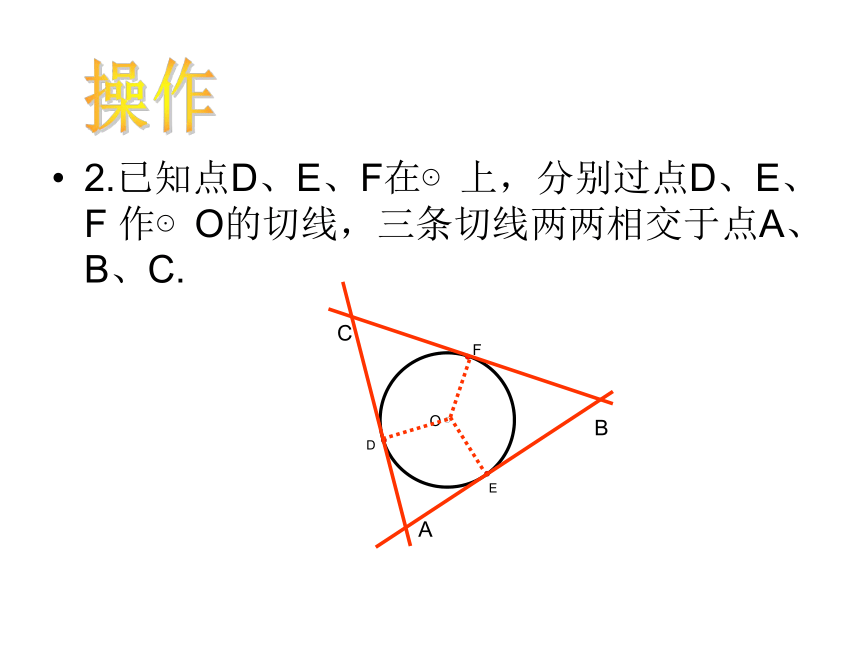
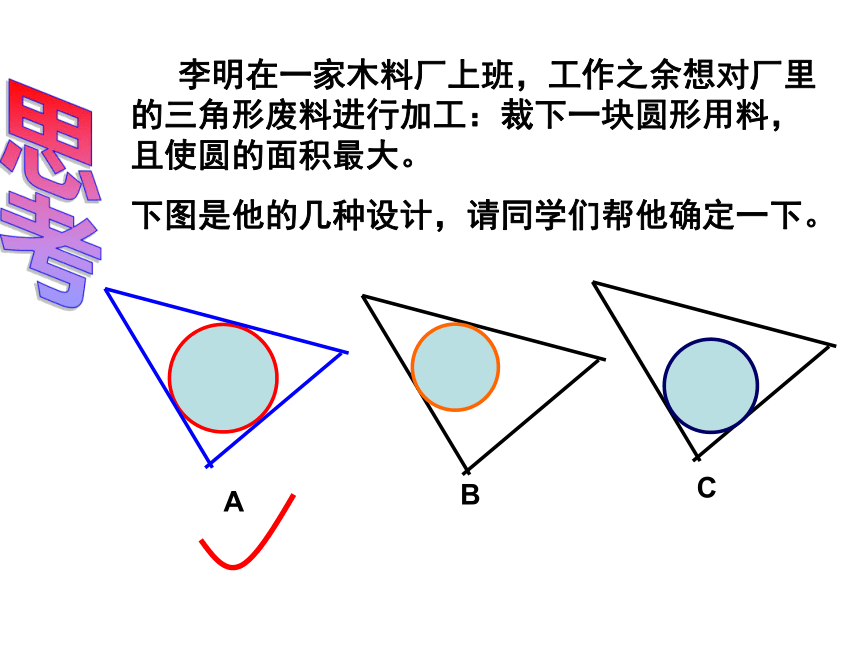
课件19张PPT。直线与圆的位置关系 (3)三角形的内切圆1.点P在⊙上，过点P作⊙O的切线。操作2.已知点D、E、F在⊙上，分别过点D、E、F 作⊙O的切线，三条切线两两相交于点A、B、C.操作ABC 李明在一家木料厂上班，工作之余想对厂里的三角形废料进行加工：裁下一块圆形用料，且使圆的面积最大。
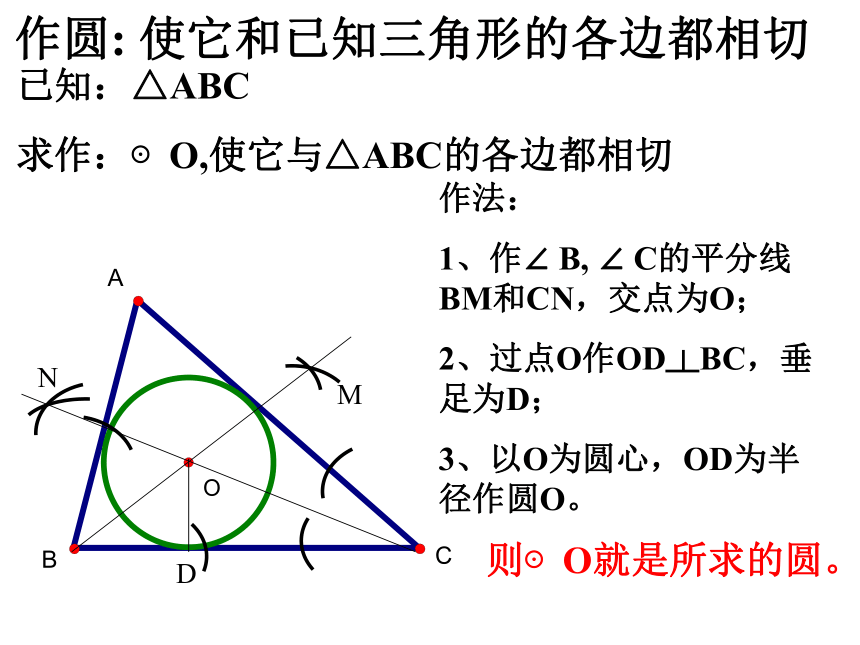
下图是他的几种设计，请同学们帮他确定一下。思考ABC作圆: 使它和已知三角形的各边都相切已知：△ABC
求作：⊙O,使它与△ABC的各边都相切则⊙O就是所求的圆。类似地，和多边形的各边都相切的圆叫做多边形的内切圆，这个多边形叫做圆的外切多边形。 概念：
与三角形各边都相切的圆叫做三角形的内切圆，内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形。想一想：根据作法,与三角形各边都相切的圆能作出几个？ 为什么？1、什么是三角形的外接圆与内切圆？
2、如何画出一个三角形的外接圆与内切圆？画圆的关键：
1、确定圆心 2、确定半径 三角形的外接圆的圆心是各边垂直平分线的交点；其半径是交点到顶点的距离。 三角形的内切圆的圆心是各内角平分线的交点；其半径是交点到一边的距离。三角形的外接圆与内切圆的比较 ①经过三角形各顶点的圆叫三角形的外接圆。
　②与三角形各边都相切的圆叫三角形的内切圆。 1、 如图1，△ABC是⊙O的 三角形。⊙ O是△ABC的 圆，点O叫△ABC的 ，它是三角形
_____ ____的交点。外接内接外心三边中垂线13、如图2，△DEF是⊙I的 三角形， ⊙I是△DEF的 圆，点I是 △DEF的_____ 心，它是________的交点。2、定义：和三角形各边都相切的圆叫做 ，内切圆的圆心叫做三角形的 ，这个三角形叫做____________ 三角形的内切圆内心圆的外切三角形外切内切内角平分线填一填 判断题：
1、三角形的内心到三角形各个顶点的距离相等( )
2、三角形的外心到三角形各边的距离相等 （ ）
3、等边三角形的内心和外心重合； （ ）
4、三角形的内心一定在三角形的内部（ ）错错对 对例1.在△ABC中，内切圆O与边BC、CA、AB分别相切于点D、E、F，∠B=60度， ∠C=70度，求∠EDF的度数OAFEDCB如果∠ A＝90 ° ，∠ BOC= °如果∠ A=120° ， ∠ BOC =　　　°如图，在△ABC中， ∠A=60 ° ，点O是内心，求∠ BOC的度数。试一试13515090 ° ＋ n °
例2:已知：点I是△ABC的内心，AI交BC于D，交外接圆于E。求证：EB=EI=EC
ABCIDE证明： 连结BI
∵I是△ABC的内心
∴∠3=∠4, ∠ 1= ∠ 2，
∵ ∠ 1= ∠ 2
∴
∴ ∠ 1= ∠ 5 , EB=EC
∴ ∠ 1+ ∠ 3= ∠ 4+ ∠ 5
∴ ∠ BIE= ∠ IBE
∴ EB=EI
又 ∵EB=EC
∴EB=EI=EC
12345例3、求等边三角形的内切圆半径r与
外接圆半径R的比。解：由等腰三角形底边上的中垂线与顶角平分线重合的性质知，等边三角形的内切圆与外接圆是两个同心圆。设内切圆切BC于D，连结OB，OD于是就有练习：3、三角形ABC中， ∠A= 50°,I是三角形的内心，
O是三角形的外心，则∠ BIC=______
∠ BOC=________40°55或125115°100°
设△ＡＢＣ的面积为Ｓ，周长为Ｌ， △ＡＢＣ内切圆
的半径为ｒ，你能
得到Ｓ＝　　Ｌｒ吗？想想：
我们学过哪些求三角形面积的公式？4. 想想，做做www.czsx.com.cn5.如图，有三条两两相交的公路a、b、c,今要在公路旁修一加油站P，使P到三条路的距离相等，你认为应修于何处？有几个选点方法？2、内心性质:
1、定义：和三角形各边都相切的圆叫做三角
形的内切圆，内切圆的圆心叫做三角形的内心，
这个三角形叫做圆的外切三角形。内心到三角形三边的距离相等；
内心与顶点连线平分内角。画三角形的内切圆:
画角平分线→定内心→定半径→画圆→结论小结与回顾?
外心（三角形外接圆的圆心）
?
三角形三边中垂线的交点（1）OA=OB=OC；
（2）外心不一定在三角形的内部．三角形三条角平分线的交点（1）到三边的距离相等；
（2）OA、OB、OC分别平分∠BAC、∠ABC、∠ACB；
（3）内心在三角形内部．作业纸书山有路勤为径