函数的单调性

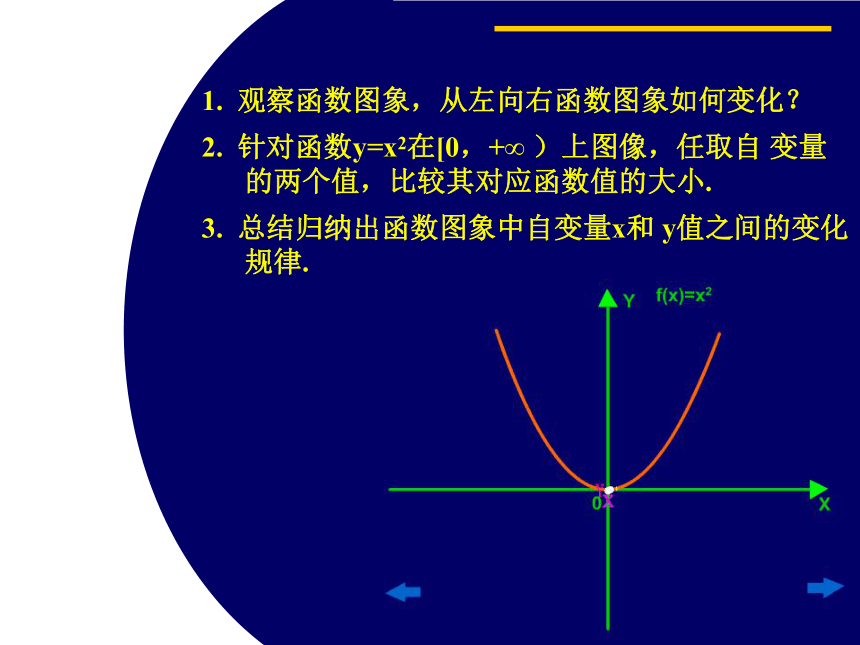
课件20张PPT。函数的单调性1. 观察函数图象，从左向右函数图象如何变化？
2. 针对函数y=x2在[0，+∞ ）上图像，任取自 变量的两个值，比较其对应函数值的大小.
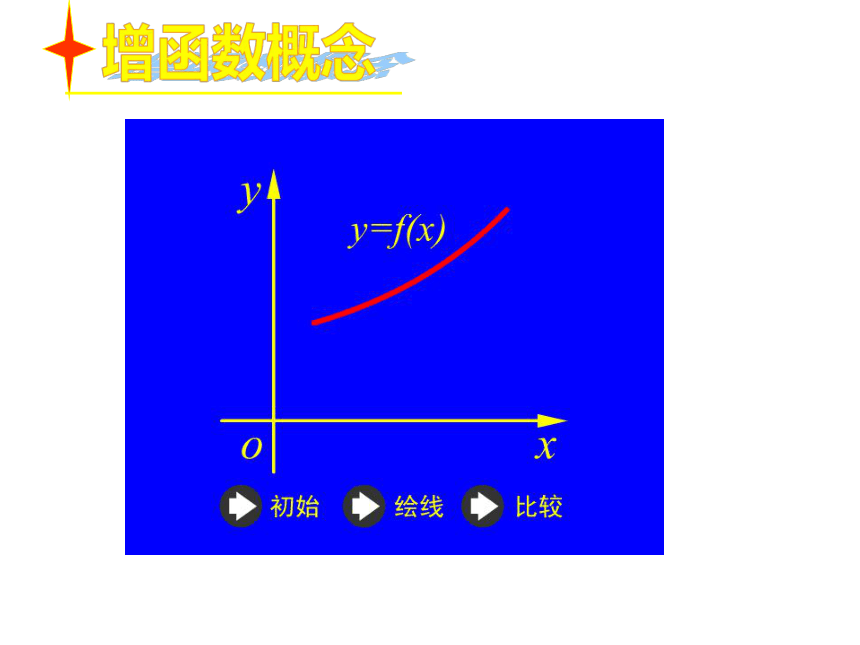
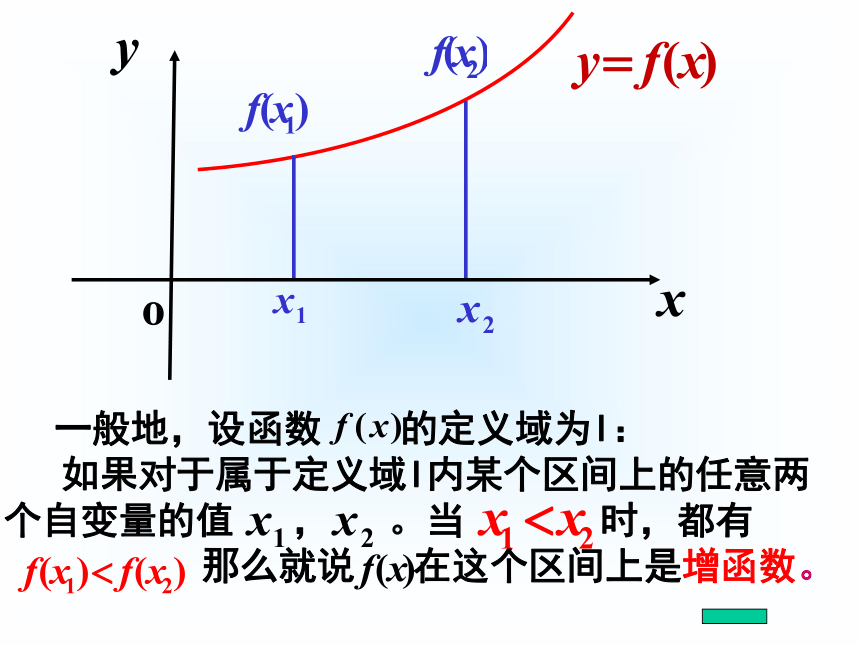
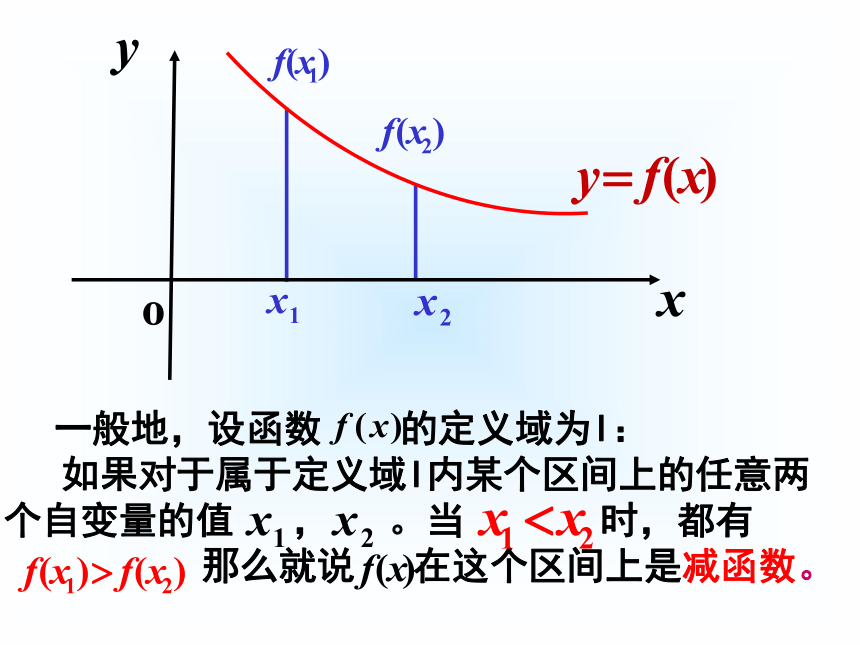
3. 总结归纳出函数图象中自变量x和 y值之间的变化规律.增函数概念减函数概念如果函数 在某个区间上是增
函数或减函数，那么就说函数
在这一区间具有（严格的）单调性，这一区间叫做 的单调区间。1.函数的单调性也叫函
数的增减性2.函数的单调性是对某个区间而言
的,它是一个局部概念.
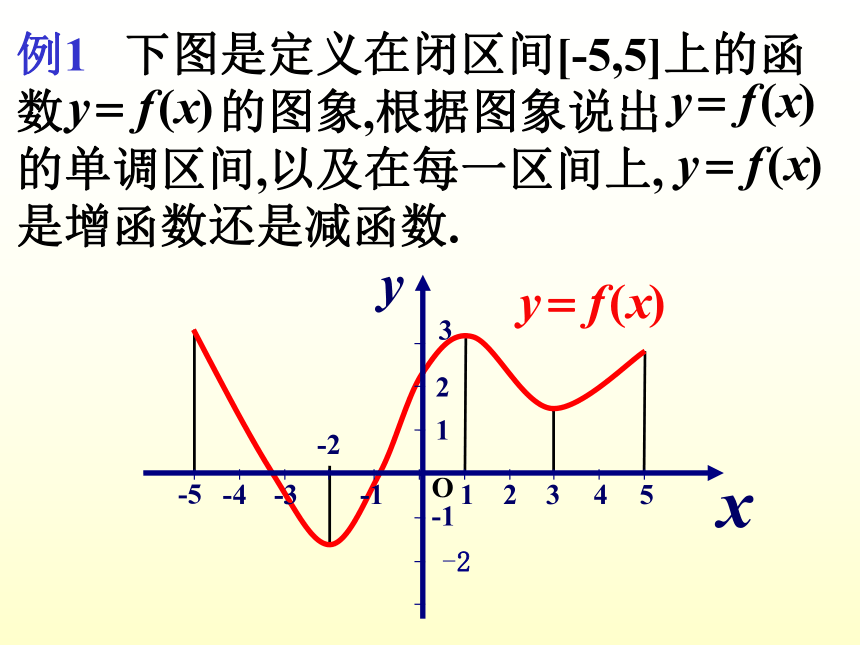
注：例1 下图是定义在闭区间[-5,5]上的函
数 的图象,根据图象说出
的单调区间,以及在每一区间上,
是增函数还是减函数.在区间[-5,-2), [1,3)上是减函数
在区间[-2,1), [3,5)上是增函数.O如图,已知 的图象(包括端点),
根据图象说出函数的单调区间,以及
在每一区间上,函数是增函数还是减
函数.如图,已知 的图象(包括端点),
根据图象说出函数的单调区间,以及
在每一区间上,函数是增函数还是减
函数.-11o练习:给出下列函数的图象,指出函数的单调区间,
并指明其单调性. 图（1） 图（2） 证明：设x1，x2是R上的任意两个实数， 且x1 f(x1)－f(x2)=(3x1+2)－(3x2+2) =3(x1－x2).
由x1 所以, f(x)=3x+2在R上是增函数.例2 证明函数 在R上是
增函数.判定函数在某个区间上的单调性的
方法步骤:1.设 给定的区间,且 ; 2.计算 至最简 ;3.判断上述差的符号 ;4.下结论(若差<0,则为增函数;
若差>0,则为减函数).例3 证明函数 在(0,+∞)上
是减函数. 例3 证明函数 在(-∞,0)上
是减函数. 例3 证明函数 在(-∞,0)上
是减函数. 由 ，得（- ∞ ，0）（- ∞ ，0 ）思考:结合图象说出函数
的单调区间,以及在各个区间上是
增函数还是减函数;你能给出相应
的证明吗?小
结 1、函数单调性是对定义域的某个区间而言的，反映的是在这一区间上函数值随自变量变化的性质.
2、判断函数单调性的方法：
（1）利用图象：
在单调区间上，增函数图象从左向右是上升的，减函数图象是下降的.
（2）利用定义：
用定义证明函数单调性的一般步骤：
任意取值→作差变形→判断符号→ 得出结论.课堂小结，知识再现