12.2三角形全等的判定第3课时 “角边角”“角角边” 分层练习(含答案) 2024—2025学年人教版数学八年级上册
文档属性
| 名称 | 12.2三角形全等的判定第3课时 “角边角”“角角边” 分层练习(含答案) 2024—2025学年人教版数学八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 298.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-29 22:47:32 | ||
图片预览



文档简介
12.2 三角形全等的判定
第 3 课时 “角边角”“角角边”
A层
知识点一 三角形全等的判定(“角边角”)
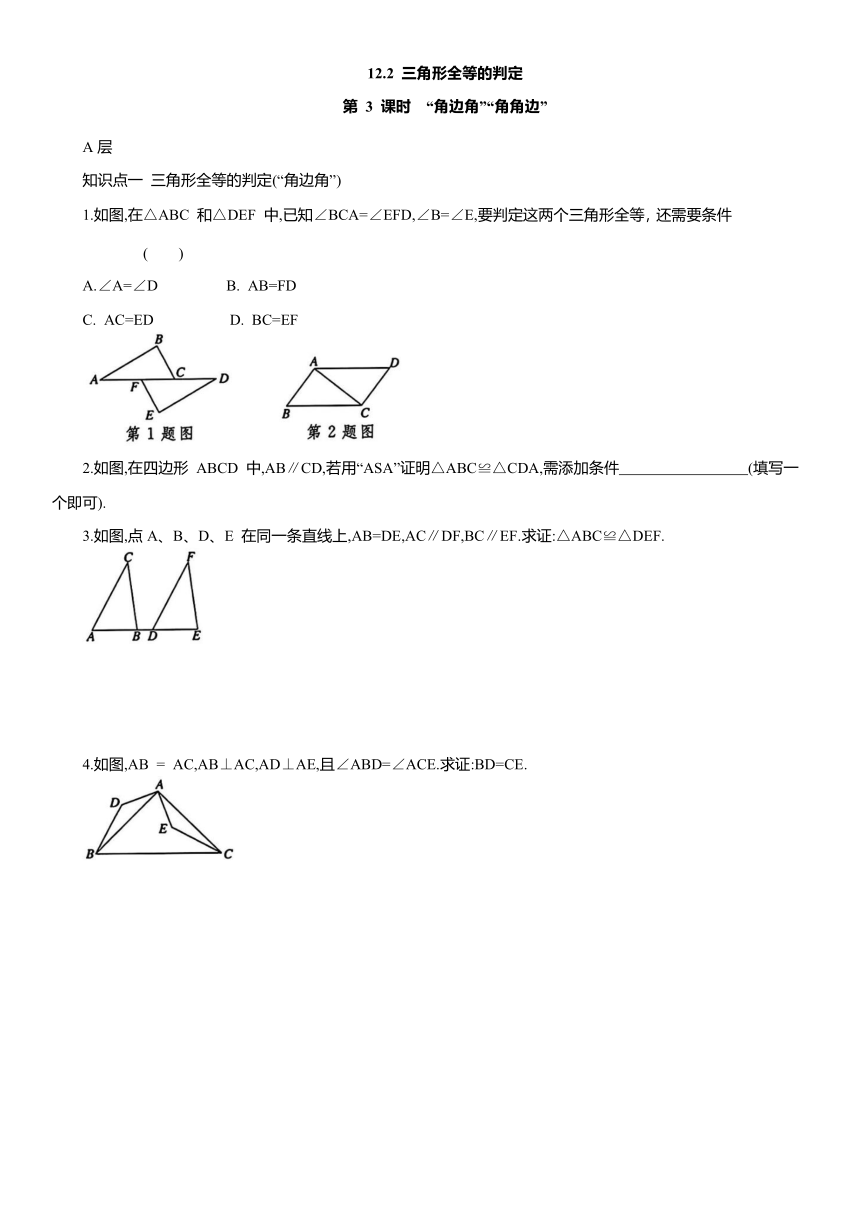
1.如图,在△ABC 和△DEF 中,已知∠BCA=∠EFD,∠B=∠E,要判定这两个三角形全等,还需要条件 ( )
A.∠A=∠D B. AB=FD
C. AC=ED D. BC=EF
2.如图,在四边形 ABCD 中,AB∥CD,若用“ASA”证明△ABC≌△CDA,需添加条件 (填写一个即可).
3.如图,点A、B、D、E 在同一条直线上,AB=DE,AC∥DF,BC∥EF.求证:△ABC≌△DEF.
4.如图,AB = AC,AB⊥AC,AD⊥AE,且∠ABD=∠ACE.求证:BD=CE.
知识点二 三角形全等的判定(“角角边”)
5.如图,已知点 B,E,C,F 在一条直线上,AC=DF,∠ACB=∠DFE,要使△ABC≌△DEF,不可以添加的条件是 ( )
A. BE=CF B.∠A=∠D
C.∠B=∠DEF D. AB=DE
6.如图,∠1=∠2,∠B =∠C,则△ABD 与△ACD (填“全等”或“不一定全等”).
7.如图,AC 是∠BAE 的平分线,点 D 是线段AC 上的一点,∠C=∠E,AB=AD.求证:BC=DE.
8.如图,D 是△ABC 的边 AB上一点,CF∥AB,DF交AC于点E,DE=EF.
(1)求证:△ADE≌△CFE;
(2)若AB=5,CF=4,求 BD 的长.
B层
9.如图,点 B 在 AE 上,若∠CBE=∠DBE,∠C=∠D,AC=5,BD=3,则四边形ADBC的周长为 ( )
A.6 B.8 C.10 D.16
10.如图,在△ABC 中,已知∠1=∠2,BE =CD,AB=5,AE=2,则CE= .
11.如图,点 D 在BC 上,AB=AD,∠C=∠E,∠BAD = ∠CAE.若∠1+ ∠2 = 108°, 则∠ABC 的度数是 .
12.如图,BD 为△ABC 的角平分线,且 BD=BC,E 在 BD 的延长线上,连接 AE,CE,∠ACE=∠ABE.求证:
(1)△ABD≌△EBC;
(2)∠BCE+∠BDC=180°.
13.如图,点 E 是 BC 的中点,点 A 在 DE 上,且∠BAE=∠CDE.作CG⊥DE 于G,BF⊥DE,交 DE 的延长线于 F.求证:
(1)EG=EF;
(2)AB=CD.
C层
14.【材料阅读】如图①,在△ABC 中,D,E 分别是 AB,AC 的中点,连接 DE,则 DE 是△ABC 的中位线,且
【结论应用】如图②,在△ABC 中,CF 平分∠ACB,且 AF⊥CF 于 点 F, BE 平 分△ABC的一个外角,且 AE⊥BE于点E.
(1)求证:EF∥BC;
(2)若 BC=5,AC=4,EF=4,求AB 的长.
第3 课时 “角边角”“角角边”
D 2.∠ACB=∠CAD(答案不唯一)
3.证明:∵AC∥DF,∴∠CAB=∠FDE.又∵BC∥EF,∴∠CBA=∠FED.在△ABC和 △DEF 中, ∴△ABC≌△DEF(ASA).
4.证明:∵AB⊥AC,AD⊥AE,∴∠BAE+
∠CAE = 90°, ∠BAE + ∠BAD = 90°.
∴∠CAE=∠BAD.∴△ABD≌△ACE
(ASA).∴BD=CE.
5. D 6.全等
7. 证 明: ∵ AC 是 ∠BAE 的 平 分 线,∴∠BAC=∠DAE.∴△BAC≌△DAE(AAS).∴BC=DE.
8.(1)略(2)解:∵△ADE≌△CFE,∴AD=CF=4.∴BD=AB-AD=5-4=1.
9. D 10.3 11.72°
12.证明:(1)∵∠ACE=∠ABE,∠ADE =∠ABE + ∠BAD = ∠ACE + ∠BEC,∴∠BAD=∠BEC.∵BD 为△ABC 的角平分线,∴∠ABD=∠EBC.在△ABD 和△EBC 中 △EBC(AAS)
(2)由(1)得△ABD≌△EBC,∴∠ADB=∠BCE. 又∵∠ADB+ ∠BDC = 180°,∴∠BCE+∠BDC=180°.
13.证明:(1)∵E 为 BC 的中点,∴BE=CE.∵ CG ⊥ DE, BF⊥ DE, ∴ ∠CGE =∠BFE = 90°. 在 △CGE 和 △BFE 中,
(AAS).∴EG=EF.
(2)∵△CGE≌△BFE,∴BF=CG.在△ABF和 △DCG 中, ∴△ABF≌△DCG(AAS).∴AB=CD.
14.(1)证明:如图②,延长 AF 交 BC于M,延长 AE 交CB 的延长线与N.∵AF⊥CF,∴∠AFC=∠MFC=90°.∵CF 平分∠ACB,∴∠ACF=∠MCF.在△ACF 和△MCF 中, ∴△ACF≌△MCF(ASA).∴AF=MF.同理AE=NE,∴EF 是△AMN 的中位线.∴EF∥MN.∴EF∥BC.
(2)解:∵AF=MF,AE =NE,∴MN=2EF=2×4=8.∵AC=4,∴CM=AC=4.∴CN=MN+CM=12.∵BC=5,∴AB=BN=CN-BC=7.
第 3 课时 “角边角”“角角边”
A层
知识点一 三角形全等的判定(“角边角”)
1.如图,在△ABC 和△DEF 中,已知∠BCA=∠EFD,∠B=∠E,要判定这两个三角形全等,还需要条件 ( )
A.∠A=∠D B. AB=FD
C. AC=ED D. BC=EF
2.如图,在四边形 ABCD 中,AB∥CD,若用“ASA”证明△ABC≌△CDA,需添加条件 (填写一个即可).
3.如图,点A、B、D、E 在同一条直线上,AB=DE,AC∥DF,BC∥EF.求证:△ABC≌△DEF.
4.如图,AB = AC,AB⊥AC,AD⊥AE,且∠ABD=∠ACE.求证:BD=CE.
知识点二 三角形全等的判定(“角角边”)
5.如图,已知点 B,E,C,F 在一条直线上,AC=DF,∠ACB=∠DFE,要使△ABC≌△DEF,不可以添加的条件是 ( )
A. BE=CF B.∠A=∠D
C.∠B=∠DEF D. AB=DE
6.如图,∠1=∠2,∠B =∠C,则△ABD 与△ACD (填“全等”或“不一定全等”).
7.如图,AC 是∠BAE 的平分线,点 D 是线段AC 上的一点,∠C=∠E,AB=AD.求证:BC=DE.
8.如图,D 是△ABC 的边 AB上一点,CF∥AB,DF交AC于点E,DE=EF.
(1)求证:△ADE≌△CFE;
(2)若AB=5,CF=4,求 BD 的长.
B层
9.如图,点 B 在 AE 上,若∠CBE=∠DBE,∠C=∠D,AC=5,BD=3,则四边形ADBC的周长为 ( )
A.6 B.8 C.10 D.16
10.如图,在△ABC 中,已知∠1=∠2,BE =CD,AB=5,AE=2,则CE= .
11.如图,点 D 在BC 上,AB=AD,∠C=∠E,∠BAD = ∠CAE.若∠1+ ∠2 = 108°, 则∠ABC 的度数是 .
12.如图,BD 为△ABC 的角平分线,且 BD=BC,E 在 BD 的延长线上,连接 AE,CE,∠ACE=∠ABE.求证:
(1)△ABD≌△EBC;
(2)∠BCE+∠BDC=180°.
13.如图,点 E 是 BC 的中点,点 A 在 DE 上,且∠BAE=∠CDE.作CG⊥DE 于G,BF⊥DE,交 DE 的延长线于 F.求证:
(1)EG=EF;
(2)AB=CD.
C层
14.【材料阅读】如图①,在△ABC 中,D,E 分别是 AB,AC 的中点,连接 DE,则 DE 是△ABC 的中位线,且
【结论应用】如图②,在△ABC 中,CF 平分∠ACB,且 AF⊥CF 于 点 F, BE 平 分△ABC的一个外角,且 AE⊥BE于点E.
(1)求证:EF∥BC;
(2)若 BC=5,AC=4,EF=4,求AB 的长.
第3 课时 “角边角”“角角边”
D 2.∠ACB=∠CAD(答案不唯一)
3.证明:∵AC∥DF,∴∠CAB=∠FDE.又∵BC∥EF,∴∠CBA=∠FED.在△ABC和 △DEF 中, ∴△ABC≌△DEF(ASA).
4.证明:∵AB⊥AC,AD⊥AE,∴∠BAE+
∠CAE = 90°, ∠BAE + ∠BAD = 90°.
∴∠CAE=∠BAD.∴△ABD≌△ACE
(ASA).∴BD=CE.
5. D 6.全等
7. 证 明: ∵ AC 是 ∠BAE 的 平 分 线,∴∠BAC=∠DAE.∴△BAC≌△DAE(AAS).∴BC=DE.
8.(1)略(2)解:∵△ADE≌△CFE,∴AD=CF=4.∴BD=AB-AD=5-4=1.
9. D 10.3 11.72°
12.证明:(1)∵∠ACE=∠ABE,∠ADE =∠ABE + ∠BAD = ∠ACE + ∠BEC,∴∠BAD=∠BEC.∵BD 为△ABC 的角平分线,∴∠ABD=∠EBC.在△ABD 和△EBC 中 △EBC(AAS)
(2)由(1)得△ABD≌△EBC,∴∠ADB=∠BCE. 又∵∠ADB+ ∠BDC = 180°,∴∠BCE+∠BDC=180°.
13.证明:(1)∵E 为 BC 的中点,∴BE=CE.∵ CG ⊥ DE, BF⊥ DE, ∴ ∠CGE =∠BFE = 90°. 在 △CGE 和 △BFE 中,
(AAS).∴EG=EF.
(2)∵△CGE≌△BFE,∴BF=CG.在△ABF和 △DCG 中, ∴△ABF≌△DCG(AAS).∴AB=CD.
14.(1)证明:如图②,延长 AF 交 BC于M,延长 AE 交CB 的延长线与N.∵AF⊥CF,∴∠AFC=∠MFC=90°.∵CF 平分∠ACB,∴∠ACF=∠MCF.在△ACF 和△MCF 中, ∴△ACF≌△MCF(ASA).∴AF=MF.同理AE=NE,∴EF 是△AMN 的中位线.∴EF∥MN.∴EF∥BC.
(2)解:∵AF=MF,AE =NE,∴MN=2EF=2×4=8.∵AC=4,∴CM=AC=4.∴CN=MN+CM=12.∵BC=5,∴AB=BN=CN-BC=7.
