北师大版数学六年级下册 (1)《第四单元复习》(课件)(共24张PPT)
文档属性
| 名称 | 北师大版数学六年级下册 (1)《第四单元复习》(课件)(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-29 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
正反比例习题课
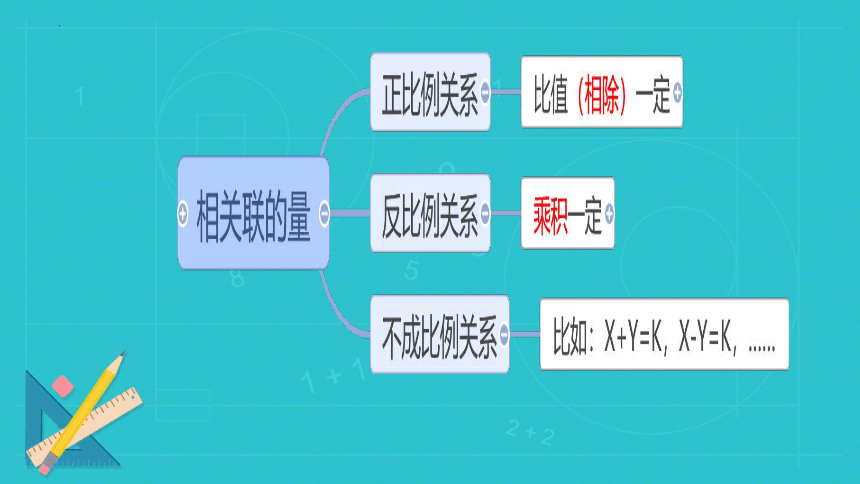
两种相关联的量,一种量的变化,另一种量也随着变化,这两种量中相对的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系,用字母表示为:
x y=k
(一定)
(1)如果A=8B(A 、B都不为0),那么A和B成( )比例。如果AB=8, 那么A和B成( )比例。
(2)如果和一定,那么两个加数( )比例。
(3)明明买一种练习册,每本1.5元,可买12本。如果用这些钱买另一种笔记本能买9本,那么这种笔记本每本( )元。题中的( )和( )是两种相关联的量,( )是一定的量,这两种相关联的量成( )比例。
1.填空
正
反
不成
2
单价
数量
总价
反
3.判断下面各题中的两种量成什么比例,并说明理由
(1)乒乓球总个数一定,每盒装的个数和需要的盒数
(2)长方形的面积一定,长方形的长和宽
(3)长方形的周长一定,长方形的长和宽
(4)划船行驶的速度一定,行驶的路程和时间
(5)每小时织布的米数 一定,织布的总米数和时间
(6)全班人数一定,男生人数和女生人数
3.(易错题)我是聪明的小法官。对的画√ 错的画×
(1)速度一定,汽车行驶的路程和时间成反比例。( )
(2)单价一定,总价和数量成正比例。 ( )
(3)小云要做16道数学题,做完的题数和没做的题数成反比 例。 ( )
(4)完成一项工程,工作效率和工作时间成反比例。 ( )
(5)将绳子剪成同样长的小段,剪成的段数和每段的长度成 正比例。( )
巩固练习
×
×
×
√
√
(1)如果a一定,那么b,c成( )比例关系。
(2)如果b一定,那么a,c成( )比例关系。
(3)如果c一定,那么a,b成( )比例关系。
巩固练习
反
正
正
6.(重点题)填表。
(1)已知A和B成正比例。
(2)已知A和B成反比例。
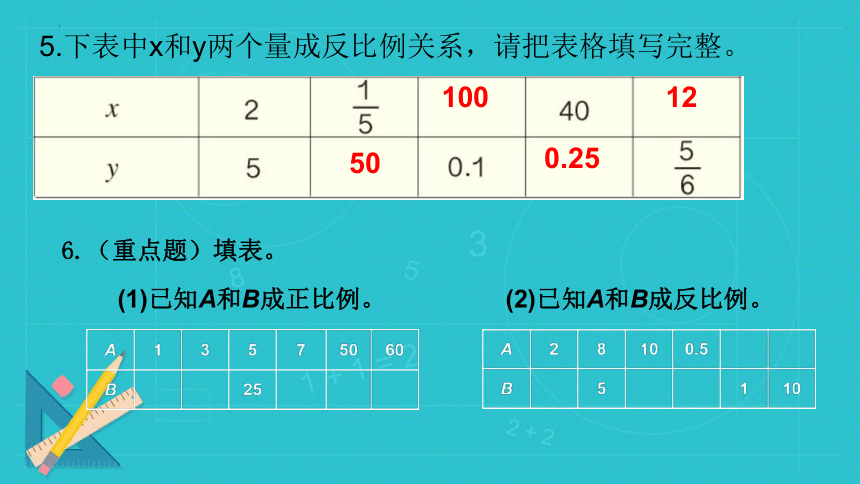
5.下表中x和y两个量成反比例关系,请把表格填写完整。
50
100
0.25
12
7. 如下图,当a=( )时,x和y成正比例;
当a=( )时,x和y成反比例。
8. xy=5,x与y成( )比例;
,x与y成( )比例。
反
正
(1)每块地砖的面积和所需地砖的数量有什么关系?
9.给一间教室铺地砖,每块地砖的面积与所需地砖的数量如下。
(3)铺这一地面用了500块地砖,所用的地砖每块面积是多大?
(2)如果每块地砖的面积是0.5m ,铺这一地面需要多少块地砖?
答:每块地砖的面积和所需块数成反比例关系.
600×0.2÷0.5=240(块)
600×0.2÷500=0.24(m2)
答:如果用每块地砖的面积是0.5m ,
铺这一地面需要240块地砖.
答:铺这一地面用了500块地砖,所用的地砖每块面积是0.24m2
例1:一个办公楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
方法一: 100×5÷25
=500÷25
=20(天)
可以先求总用电量,再求现在的用电天数。
一个办公楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
思考:
(1)题中有哪两种相关联的量?
(2)这两种相关联的量成什么比例关系?你是怎么判断的?
(3) 你能根据这样的比例关系列出一个含有未知数的比例式吗?
解:设原来5天的用电量现在可以用x天。
答:原来5天的用电量现在可以用20天。
回顾与反思
解这个问题的关键是找到哪两个量的乘积一定。
只要两个量的乘积一定,就可以用反比例关系解答。
现在30天的用电量原来只够用多少天?
解:设现在30天的用电量原来只够用x天。
答:现在30天的用电量原来只够用7.5天。
考考你
举一反三:
笑笑带了一些钱去文具店买文具,买单价是2元的签字笔正好可以买14支,如果用这些钱买单价是3.5元的签字笔可以买多少支?
方法一:
14×2÷3.5=8(支)
方法二:
解:设可以买X支
3.5X=14×2
3.5X=28
X=8
课堂小结
用反比例知识解决问题的解题步骤:
①根据不变量,判断题中哪两种相关联的量成反比例。
②找出两组相对应的数,并设出未知数,列出方程。
③解比例。
④检验并写出答语。
用正比例知识解决问题的解题步骤:
①根据不变量,判断题中哪两种相关联的量成正比例。
②找出两组相对应的数,并设出未知数,列出比例。
③解比例。
④检验并写出答语。
习题巩固
1.小明买4支圆珠笔用了6元,小刚想买3支同样的圆珠笔,要用多少钱?
解:设买3支同样的圆珠笔,要用x元。
答:买3支同样的圆珠笔,要用4.5元。
2.学校小商店有两种圆珠笔,小明带的钱刚好可以买4支单价是1.5元的。如果他只买单价是2元的,可以买多少支?
解:设可以买x支。
答:可以买3支。
用正、反比例知识解决问题的异同点。
同
这两类题都是用比例知识解答,解题思路相同。
异
用正比例知识解决问题是根据比值一定列出比例,用反比例知识解决问题是根据积一定列出比例。
3、一个办公楼5天照明用电500千瓦时。照这样计算,750千瓦时的电,可以用多少天?(用比例解答)
解:设750千瓦时的电可以用x天。
答:可以用7.5天
4.工程队修一条水渠,每天工作6小时,12天可以完成。如果每小时的工作量不变,每天工作8小时,多少天可以完成任务?
解:设x天可以完成任务。
答:9天可以完成任务。
5.小林读一本文学名著,如果每天读30页,8天可以读完。小林想6天读完,那么平均每天要读多少页?
解:设平均每天要读x页。
答:平均每天要读40页。
总结与思考
正反比例习题课
两种相关联的量,一种量的变化,另一种量也随着变化,这两种量中相对的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系,用字母表示为:
x y=k
(一定)
(1)如果A=8B(A 、B都不为0),那么A和B成( )比例。如果AB=8, 那么A和B成( )比例。
(2)如果和一定,那么两个加数( )比例。
(3)明明买一种练习册,每本1.5元,可买12本。如果用这些钱买另一种笔记本能买9本,那么这种笔记本每本( )元。题中的( )和( )是两种相关联的量,( )是一定的量,这两种相关联的量成( )比例。
1.填空
正
反
不成
2
单价
数量
总价
反
3.判断下面各题中的两种量成什么比例,并说明理由
(1)乒乓球总个数一定,每盒装的个数和需要的盒数
(2)长方形的面积一定,长方形的长和宽
(3)长方形的周长一定,长方形的长和宽
(4)划船行驶的速度一定,行驶的路程和时间
(5)每小时织布的米数 一定,织布的总米数和时间
(6)全班人数一定,男生人数和女生人数
3.(易错题)我是聪明的小法官。对的画√ 错的画×
(1)速度一定,汽车行驶的路程和时间成反比例。( )
(2)单价一定,总价和数量成正比例。 ( )
(3)小云要做16道数学题,做完的题数和没做的题数成反比 例。 ( )
(4)完成一项工程,工作效率和工作时间成反比例。 ( )
(5)将绳子剪成同样长的小段,剪成的段数和每段的长度成 正比例。( )
巩固练习
×
×
×
√
√
(1)如果a一定,那么b,c成( )比例关系。
(2)如果b一定,那么a,c成( )比例关系。
(3)如果c一定,那么a,b成( )比例关系。
巩固练习
反
正
正
6.(重点题)填表。
(1)已知A和B成正比例。
(2)已知A和B成反比例。
5.下表中x和y两个量成反比例关系,请把表格填写完整。
50
100
0.25
12
7. 如下图,当a=( )时,x和y成正比例;
当a=( )时,x和y成反比例。
8. xy=5,x与y成( )比例;
,x与y成( )比例。
反
正
(1)每块地砖的面积和所需地砖的数量有什么关系?
9.给一间教室铺地砖,每块地砖的面积与所需地砖的数量如下。
(3)铺这一地面用了500块地砖,所用的地砖每块面积是多大?
(2)如果每块地砖的面积是0.5m ,铺这一地面需要多少块地砖?
答:每块地砖的面积和所需块数成反比例关系.
600×0.2÷0.5=240(块)
600×0.2÷500=0.24(m2)
答:如果用每块地砖的面积是0.5m ,
铺这一地面需要240块地砖.
答:铺这一地面用了500块地砖,所用的地砖每块面积是0.24m2
例1:一个办公楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
方法一: 100×5÷25
=500÷25
=20(天)
可以先求总用电量,再求现在的用电天数。
一个办公楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
思考:
(1)题中有哪两种相关联的量?
(2)这两种相关联的量成什么比例关系?你是怎么判断的?
(3) 你能根据这样的比例关系列出一个含有未知数的比例式吗?
解:设原来5天的用电量现在可以用x天。
答:原来5天的用电量现在可以用20天。
回顾与反思
解这个问题的关键是找到哪两个量的乘积一定。
只要两个量的乘积一定,就可以用反比例关系解答。
现在30天的用电量原来只够用多少天?
解:设现在30天的用电量原来只够用x天。
答:现在30天的用电量原来只够用7.5天。
考考你
举一反三:
笑笑带了一些钱去文具店买文具,买单价是2元的签字笔正好可以买14支,如果用这些钱买单价是3.5元的签字笔可以买多少支?
方法一:
14×2÷3.5=8(支)
方法二:
解:设可以买X支
3.5X=14×2
3.5X=28
X=8
课堂小结
用反比例知识解决问题的解题步骤:
①根据不变量,判断题中哪两种相关联的量成反比例。
②找出两组相对应的数,并设出未知数,列出方程。
③解比例。
④检验并写出答语。
用正比例知识解决问题的解题步骤:
①根据不变量,判断题中哪两种相关联的量成正比例。
②找出两组相对应的数,并设出未知数,列出比例。
③解比例。
④检验并写出答语。
习题巩固
1.小明买4支圆珠笔用了6元,小刚想买3支同样的圆珠笔,要用多少钱?
解:设买3支同样的圆珠笔,要用x元。
答:买3支同样的圆珠笔,要用4.5元。
2.学校小商店有两种圆珠笔,小明带的钱刚好可以买4支单价是1.5元的。如果他只买单价是2元的,可以买多少支?
解:设可以买x支。
答:可以买3支。
用正、反比例知识解决问题的异同点。
同
这两类题都是用比例知识解答,解题思路相同。
异
用正比例知识解决问题是根据比值一定列出比例,用反比例知识解决问题是根据积一定列出比例。
3、一个办公楼5天照明用电500千瓦时。照这样计算,750千瓦时的电,可以用多少天?(用比例解答)
解:设750千瓦时的电可以用x天。
答:可以用7.5天
4.工程队修一条水渠,每天工作6小时,12天可以完成。如果每小时的工作量不变,每天工作8小时,多少天可以完成任务?
解:设x天可以完成任务。
答:9天可以完成任务。
5.小林读一本文学名著,如果每天读30页,8天可以读完。小林想6天读完,那么平均每天要读多少页?
解:设平均每天要读x页。
答:平均每天要读40页。
总结与思考
