第17章 函数及其图像 单元检测 (无答案) 华师大版八年级下册数学
文档属性
| 名称 | 第17章 函数及其图像 单元检测 (无答案) 华师大版八年级下册数学 |  | |
| 格式 | docx | ||
| 文件大小 | 47.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-29 23:09:01 | ||
图片预览


文档简介
(
1
) (
3
) (
2
)
(
第
1
7
章
质量评估
(时间:120分钟 满分:120分
)
班级_______________ 姓名________________ 考号________________
题号
一
二
三
总分
得分
选择题(每小题
3
分,共
30
分)
1
、
若点
A (-3, a ), B (1, b
)都在直线
y =5x-2
上,则
a
与
b
的大小关系是
(
)
A . a > b
B . a = b
C . a < b
D
.无法确定
2
、
将直线
y =2x-2
向上平移
4
个单位长度后,所得的直线的解析式为
(
)
A . y =2x
B . y =2x-4
C . y =2x+2
D . y =2x-6
3
、
如图,直线
y
1
= kx + b
与直线
y
2
=- x +5
交于点(
1, m )
,则不等式
y
1
2
的解集为
(
)
A.x<1
B.x>1
C.x
≤
1
D.x
≥
1
4
、王
大爷要围成一个矩形菜园,菜园的一边
是
墙,用篱笆围成的另外三边总长应恰好为
24
米.要围成的菜园是如图所示的矩形
ABCD
.设
BC
边的长为
x
米,
AB
边的长为
y
米,则
y
与
x
之间的函数关系式是(
)
A . y =-2x+24(0< x <12)
B
.
y =
x +12(0< x <24)
C . y =2x-24(0< x <12)
D . y =
x -12(0< x <24)
5
、
购物狂欢节期间,
官方
旗舰店在平台推出优惠活动,对于标价超过
500
元的服饰先按标价减免
50
元再打六折,小
赵
在该平台购买了标价
x
元的服饰(
x >500)
,则应付款
y
(元)与商品标价
x
(元)的关系式为
(
)
A . y =0.6( x -50)
B . y =0.4( x -50)
C . y =0.6x-50
D . y =0.4x-50
)
(
O
) (
第
4
题
) (
A
) (
C
) (
D
) (
B
) (
菜园
) (
墙
) (
第
3
题
) (
y2
) (
y
1
) (
y
) (
X
)
(
C
) (
B
) (
A
) (
x/h
) (
y/km
) (
240
) (
6
) (
4
) (
第
10
题
) (
O
) (
第
9
题
) (
6
、
若点
4(-4, a ), B (1, b ),
C (3, c
)都在反比例函数
y =
上,则
a , b , c
的大小关系正确的是
( )
A . a < b <
c
B . a < c < b
C . b < c < a
D . c < b < a
7
、
平面直角坐标系内,点
M
(
5
,
3
)在
第
(
)
A
.
一
B
.
x
轴上
C
.
三
D
.
y
轴上
8
、若点
P
(
3m-1,3
)在第二象限,则
m
取值范围为(
)
A
.
m
>
B.m
<
C.m
≥
D.m
≤
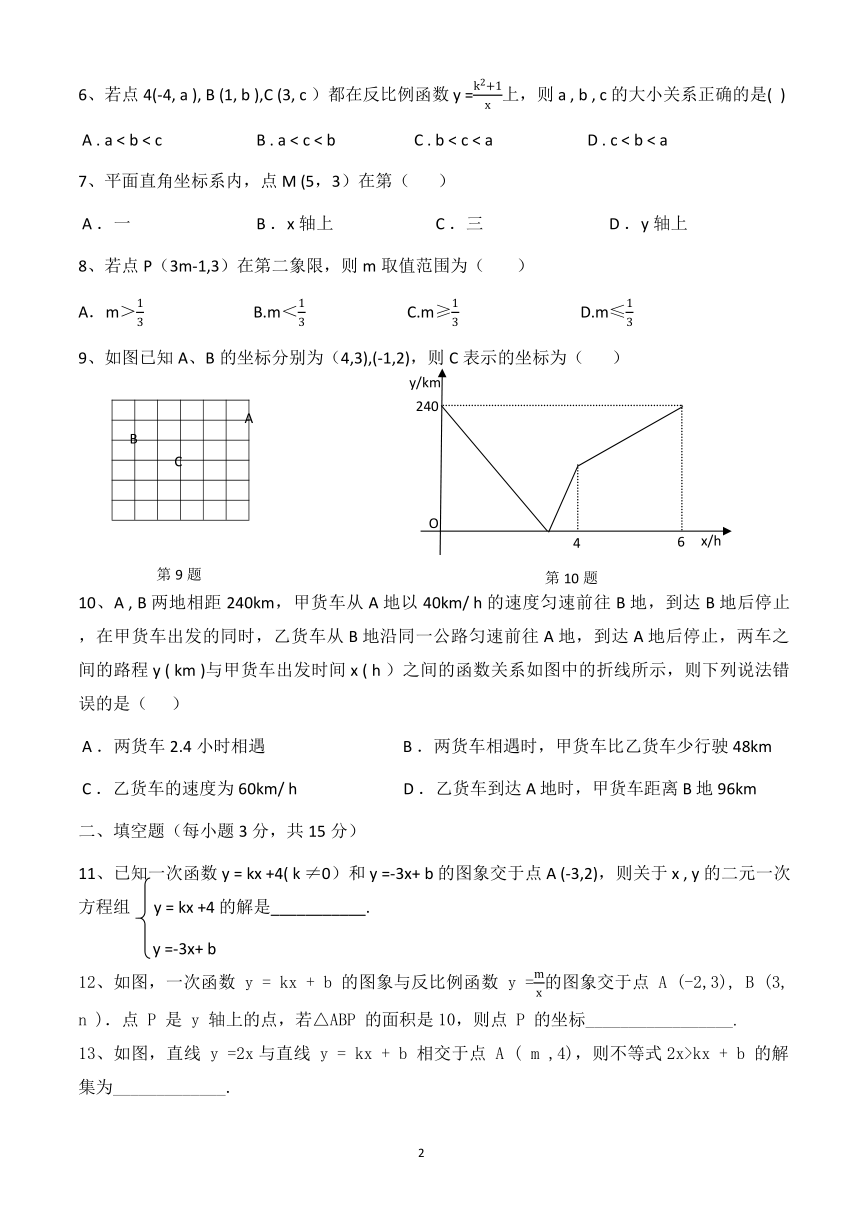
9
、如图
已知
A
、
B
的
坐标分别为(
4,3),(
-1,2
)
,则
C
表示的坐标为
(
)
10
、
A , B
两地相距
240km
,甲货车从
A
地以
40km/ h
的速度匀速前往
B
地,到达
B
地后停止,在甲货车出发的同时,乙货车从
B
地沿同一公路匀速前往
A
地,到达
A
地后停止,两车之间的路程
y ( km )
与甲货车出发时间
x ( h
)之间的函数关系如图中的折线所示,则下列说法错误的是
(
)
A
.两货车
2.4
小时相遇
B
.两货车相遇时,甲货车比乙货车少行驶
48km
C
.乙货车的速度为
60km/ h
D
.乙货车到达
A
地时,甲货车距离
B
地
96km
二、填空题
(每小题
3
分,共
15
分)
11
、
已知一次函数
y = kx +4( k
≠
0
)和
y =-3x+ b
的图象交于点
A (-3,2)
,则关于
x , y
的二元一次方程组
y = kx +4
的解是
___________.
y =-3x+ b
12、
如图,一次函数 y = kx + b 的图象与反比例函数 y =
的图象交于点 A (-2,3), B (3, n ).点 P 是 y 轴上的点,若△ABP 的面积是10,则点 P
的坐标_________________
.
13、如图,直线 y =2x与直线 y = kx + b 相交于点 A ( m ,4),则不等式2x>kx + b 的解集为_____________.
)
(
y
) (
14
、如图所示,点
A , B , C
在反比例函数
y=
( k >0, x >0
)的图象上,连接
OA
,
OB , OC
,分别过点
A , B , C
三点作
x
轴的垂线,垂足分别为
M , N , P
.若
OM = MN = NP
,且图中三块阴影部分的面积之和为
62
,则
k
的值是
______________.
15、正方形 A
1
B
1
C
1
O 、A
2
B
2
C
2
C
1
、A
3
B
3
C
3
C
2
,…按如图所示放置,点A
1
,A
2
,A
3
,……和 C
1
,C
2
, C
3
,……分别在直线 y =- x +1和 x 轴上,则点 B
2025
的纵坐标是_________,点 B
n
的纵坐标是__________.
三、解答题(共75分)
16、(8分)
如图,在△ ABC 中, BC 边上的高是定值.当三角形的顶点 C 沿底边所在直线由点 B 向右运动时,三角形的面积随之发生变化.设底边长 BC = xcm ,三角形面积为ycm2,变化情况如下表所示:
)
(
y
)
(
A ( m ,4)
)
(
A
)
(
O
) (
X
)
(
B
)
(
O
)
(
x
)
(
第
13
题
) (
第
12
题
)
(
y
)
(
y
)
(
A
)
(
B3
) (
A3
) (
B
)
(
B
2
) (
A
2
) (
C
)
(
A
1
) (
B
1
)
(
C
2
) (
x
)
(
C3
) (
C
1
) (
O
) (
X
) (
M
) (
N
) (
P
) (
O
)
(
第
15
题
) (
第
14
题
)
(
底边长
x
(
cm
)
1
2
三角形面积
3
6
) (
C
) (
C
) (
C
) (
C
) (
A
) (
B
)
(
品种
成本(万元/亩)
售价(万元/亩)
A
1.1
2.2
B
1.3
2.7
) (
(1)在这个变化过程中,自变量是
____________.因变量是___________.
(2)由上表可知, BC 边上的高为
_____________
cm
.
(3) y 与 x 的关系式可以表示为
______________.
(4)当底边长由3cm变化到12cm时,三角形的面积从
______
cm
2
变化到
______
cm
2
.
17、(8分)
已知点 P (-3a-4,2+ a ),解答下列各题:
(1)若点 p 在 x 轴上,则点 p
的坐标为_____________.
(2)若 Q (5,8),且 PQ
∥
y 轴,则点 p
的坐标为____________.
(3)若点 p 在第二象限,且它到 x 轴、 y 轴的距离相等,求
a
2023+2024
的值.
18、(10分)
政府大力实施"百千万工程",推动乡村振兴特色产业.湘桥区某水果生产基地在政府的支持下种植了 A 、 B 两个品种的"潮州柑"共50亩,两种品种的"潮州柑"成本和售价如下表所示,设种植 A 品种"潮州柑" x 亩,若50亩地全部种植两种"潮州柑"共获得利润 y 万元.
(
1
)
求
y
与
x
之间的函数关系式;
(
2
)
若
A
品种
"
潮州柑
"
的种植亩数不少于
B
品种
"
潮州柑
"
种植亩数的
1.5
倍,则种植
A
品种
"
潮州柑
"
多少亩时,该水果生产基地
利润最大?并求出最大利润
.
19
、(
10
分)
点
O
为平面直角坐标系的原点,点
P ( x , y
)在第一象限,且
x + y =6
,点
A
的坐标为(
4,0)
.设
△
OPA
的面积为
S .
(1
)当点
p
的横坐标是
4
时,求△
OPA
的面积;
(2
)用含
x
的式子表示
S
,并写出
x
的取值范围;
(3
)求△
OPA
周长的最小值.
)
(
10
) (
5
) (
75
) (
120
) (
y/
元
) (
x/
千克
) (
O
) (
5
) (
-1
) (
B
) (
M
) (
A
) (
D
) (
y
) (
X
) (
O
) (
20、(10分)
如图直线:
y
1
= kx + b 经过点4(-6,0), B (-1
,
5).
(1)求直线 AB 的表达式;
(2)若直线y
2
=-2x-3与直线 AB 相交于点 M ,
求点 M 的坐标;
(3)根据图象,直接写出关于 x 的不等式
kx + b >-2x-3≥
0的解集.
21、(10分)
因活动需要购买某种水果,数学活动小组的同学通过市场调查得知:在甲商店购买该水果的费用
y
1
(元)与该水果的质量 x (千克)之间的关系如图所示;在乙商店购买该水果的费用y
2
(元)与
该水果的质量 x (千克)之间的函数解析式为y
2
=10x( x ≥0).
(1)求 y 与 x 之间的函数解析式;
(2)现计划用660元购买该水果,选甲、乙
哪家商店能购买该水果更多一些
?
)
(
50
) (
30
) (
20
) (
15
) (
1400
) (
1800
) (
2600
) (
B
) (
A
) (
距离(米)
) (
时间(分钟)
) (
O
) (
C
) (
A
) (
B
) (
-4
) (
-3
) (
-2
) (
-1
) (
5
) (
4
) (
3
) (
2
) (
1
) (
-5
) (
-4
) (
-3
) (
-2
) (
-1
) (
4
) (
3
) (
2
) (
1
) (
0
) (
22
、
(
7
分)
如图,已知
A (-2,3)
、
B (4,3)
、
C (-1,-3)
(1
)求点
C
到
x
轴的距离;
(2
)求△
ABC
的面积;
(3
)点
P
在
y
轴上,当△
ABP
的面积
为
6
时,请直接写出点
P
的坐标
.
23
、
(
12
分)
小萌
放学步行从学校回家,当她走了一段路后,想起要去买彩笔做画报,于是原路返回到刚经过的文具用品店,买到彩笔后继续往家走,如图是她离家的距离与所用时间的关系示意图,请根据图中提供的信息回答下列问题:
(1
)小颖家与学校的距离是多少米?
(2
)点
A
表示的实际意义是什么?
(3
)小颖本次从学校回家的整个过程中,走过的路程是多少米?
(4
)买到彩笔后,小颖从文具用品店回到家步行的速度是多少米
/
分?
)
1
6
1
) (
3
) (
2
)
(
第
1
7
章
质量评估
(时间:120分钟 满分:120分
)
班级_______________ 姓名________________ 考号________________
题号
一
二
三
总分
得分
选择题(每小题
3
分,共
30
分)
1
、
若点
A (-3, a ), B (1, b
)都在直线
y =5x-2
上,则
a
与
b
的大小关系是
(
)
A . a > b
B . a = b
C . a < b
D
.无法确定
2
、
将直线
y =2x-2
向上平移
4
个单位长度后,所得的直线的解析式为
(
)
A . y =2x
B . y =2x-4
C . y =2x+2
D . y =2x-6
3
、
如图,直线
y
1
= kx + b
与直线
y
2
=- x +5
交于点(
1, m )
,则不等式
y
1
的解集为
(
)
A.x<1
B.x>1
C.x
≤
1
D.x
≥
1
4
、王
大爷要围成一个矩形菜园,菜园的一边
是
墙,用篱笆围成的另外三边总长应恰好为
24
米.要围成的菜园是如图所示的矩形
ABCD
.设
BC
边的长为
x
米,
AB
边的长为
y
米,则
y
与
x
之间的函数关系式是(
)
A . y =-2x+24(0< x <12)
B
.
y =
x +12(0< x <24)
C . y =2x-24(0< x <12)
D . y =
x -12(0< x <24)
5
、
购物狂欢节期间,
官方
旗舰店在平台推出优惠活动,对于标价超过
500
元的服饰先按标价减免
50
元再打六折,小
赵
在该平台购买了标价
x
元的服饰(
x >500)
,则应付款
y
(元)与商品标价
x
(元)的关系式为
(
)
A . y =0.6( x -50)
B . y =0.4( x -50)
C . y =0.6x-50
D . y =0.4x-50
)
(
O
) (
第
4
题
) (
A
) (
C
) (
D
) (
B
) (
菜园
) (
墙
) (
第
3
题
) (
y2
) (
y
1
) (
y
) (
X
)
(
C
) (
B
) (
A
) (
x/h
) (
y/km
) (
240
) (
6
) (
4
) (
第
10
题
) (
O
) (
第
9
题
) (
6
、
若点
4(-4, a ), B (1, b ),
C (3, c
)都在反比例函数
y =
上,则
a , b , c
的大小关系正确的是
( )
A . a < b <
c
B . a < c < b
C . b < c < a
D . c < b < a
7
、
平面直角坐标系内,点
M
(
5
,
3
)在
第
(
)
A
.
一
B
.
x
轴上
C
.
三
D
.
y
轴上
8
、若点
P
(
3m-1,3
)在第二象限,则
m
取值范围为(
)
A
.
m
>
B.m
<
C.m
≥
D.m
≤
9
、如图
已知
A
、
B
的
坐标分别为(
4,3),(
-1,2
)
,则
C
表示的坐标为
(
)
10
、
A , B
两地相距
240km
,甲货车从
A
地以
40km/ h
的速度匀速前往
B
地,到达
B
地后停止,在甲货车出发的同时,乙货车从
B
地沿同一公路匀速前往
A
地,到达
A
地后停止,两车之间的路程
y ( km )
与甲货车出发时间
x ( h
)之间的函数关系如图中的折线所示,则下列说法错误的是
(
)
A
.两货车
2.4
小时相遇
B
.两货车相遇时,甲货车比乙货车少行驶
48km
C
.乙货车的速度为
60km/ h
D
.乙货车到达
A
地时,甲货车距离
B
地
96km
二、填空题
(每小题
3
分,共
15
分)
11
、
已知一次函数
y = kx +4( k
≠
0
)和
y =-3x+ b
的图象交于点
A (-3,2)
,则关于
x , y
的二元一次方程组
y = kx +4
的解是
___________.
y =-3x+ b
12、
如图,一次函数 y = kx + b 的图象与反比例函数 y =
的图象交于点 A (-2,3), B (3, n ).点 P 是 y 轴上的点,若△ABP 的面积是10,则点 P
的坐标_________________
.
13、如图,直线 y =2x与直线 y = kx + b 相交于点 A ( m ,4),则不等式2x>kx + b 的解集为_____________.
)
(
y
) (
14
、如图所示,点
A , B , C
在反比例函数
y=
( k >0, x >0
)的图象上,连接
OA
,
OB , OC
,分别过点
A , B , C
三点作
x
轴的垂线,垂足分别为
M , N , P
.若
OM = MN = NP
,且图中三块阴影部分的面积之和为
62
,则
k
的值是
______________.
15、正方形 A
1
B
1
C
1
O 、A
2
B
2
C
2
C
1
、A
3
B
3
C
3
C
2
,…按如图所示放置,点A
1
,A
2
,A
3
,……和 C
1
,C
2
, C
3
,……分别在直线 y =- x +1和 x 轴上,则点 B
2025
的纵坐标是_________,点 B
n
的纵坐标是__________.
三、解答题(共75分)
16、(8分)
如图,在△ ABC 中, BC 边上的高是定值.当三角形的顶点 C 沿底边所在直线由点 B 向右运动时,三角形的面积随之发生变化.设底边长 BC = xcm ,三角形面积为ycm2,变化情况如下表所示:
)
(
y
)
(
A ( m ,4)
)
(
A
)
(
O
) (
X
)
(
B
)
(
O
)
(
x
)
(
第
13
题
) (
第
12
题
)
(
y
)
(
y
)
(
A
)
(
B3
) (
A3
) (
B
)
(
B
2
) (
A
2
) (
C
)
(
A
1
) (
B
1
)
(
C
2
) (
x
)
(
C3
) (
C
1
) (
O
) (
X
) (
M
) (
N
) (
P
) (
O
)
(
第
15
题
) (
第
14
题
)
(
底边长
x
(
cm
)
1
2
三角形面积
3
6
) (
C
) (
C
) (
C
) (
C
) (
A
) (
B
)
(
品种
成本(万元/亩)
售价(万元/亩)
A
1.1
2.2
B
1.3
2.7
) (
(1)在这个变化过程中,自变量是
____________.因变量是___________.
(2)由上表可知, BC 边上的高为
_____________
cm
.
(3) y 与 x 的关系式可以表示为
______________.
(4)当底边长由3cm变化到12cm时,三角形的面积从
______
cm
2
变化到
______
cm
2
.
17、(8分)
已知点 P (-3a-4,2+ a ),解答下列各题:
(1)若点 p 在 x 轴上,则点 p
的坐标为_____________.
(2)若 Q (5,8),且 PQ
∥
y 轴,则点 p
的坐标为____________.
(3)若点 p 在第二象限,且它到 x 轴、 y 轴的距离相等,求
a
2023+2024
的值.
18、(10分)
政府大力实施"百千万工程",推动乡村振兴特色产业.湘桥区某水果生产基地在政府的支持下种植了 A 、 B 两个品种的"潮州柑"共50亩,两种品种的"潮州柑"成本和售价如下表所示,设种植 A 品种"潮州柑" x 亩,若50亩地全部种植两种"潮州柑"共获得利润 y 万元.
(
1
)
求
y
与
x
之间的函数关系式;
(
2
)
若
A
品种
"
潮州柑
"
的种植亩数不少于
B
品种
"
潮州柑
"
种植亩数的
1.5
倍,则种植
A
品种
"
潮州柑
"
多少亩时,该水果生产基地
利润最大?并求出最大利润
.
19
、(
10
分)
点
O
为平面直角坐标系的原点,点
P ( x , y
)在第一象限,且
x + y =6
,点
A
的坐标为(
4,0)
.设
△
OPA
的面积为
S .
(1
)当点
p
的横坐标是
4
时,求△
OPA
的面积;
(2
)用含
x
的式子表示
S
,并写出
x
的取值范围;
(3
)求△
OPA
周长的最小值.
)
(
10
) (
5
) (
75
) (
120
) (
y/
元
) (
x/
千克
) (
O
) (
5
) (
-1
) (
B
) (
M
) (
A
) (
D
) (
y
) (
X
) (
O
) (
20、(10分)
如图直线:
y
1
= kx + b 经过点4(-6,0), B (-1
,
5).
(1)求直线 AB 的表达式;
(2)若直线y
2
=-2x-3与直线 AB 相交于点 M ,
求点 M 的坐标;
(3)根据图象,直接写出关于 x 的不等式
kx + b >-2x-3≥
0的解集.
21、(10分)
因活动需要购买某种水果,数学活动小组的同学通过市场调查得知:在甲商店购买该水果的费用
y
1
(元)与该水果的质量 x (千克)之间的关系如图所示;在乙商店购买该水果的费用y
2
(元)与
该水果的质量 x (千克)之间的函数解析式为y
2
=10x( x ≥0).
(1)求 y 与 x 之间的函数解析式;
(2)现计划用660元购买该水果,选甲、乙
哪家商店能购买该水果更多一些
?
)
(
50
) (
30
) (
20
) (
15
) (
1400
) (
1800
) (
2600
) (
B
) (
A
) (
距离(米)
) (
时间(分钟)
) (
O
) (
C
) (
A
) (
B
) (
-4
) (
-3
) (
-2
) (
-1
) (
5
) (
4
) (
3
) (
2
) (
1
) (
-5
) (
-4
) (
-3
) (
-2
) (
-1
) (
4
) (
3
) (
2
) (
1
) (
0
) (
22
、
(
7
分)
如图,已知
A (-2,3)
、
B (4,3)
、
C (-1,-3)
(1
)求点
C
到
x
轴的距离;
(2
)求△
ABC
的面积;
(3
)点
P
在
y
轴上,当△
ABP
的面积
为
6
时,请直接写出点
P
的坐标
.
23
、
(
12
分)
小萌
放学步行从学校回家,当她走了一段路后,想起要去买彩笔做画报,于是原路返回到刚经过的文具用品店,买到彩笔后继续往家走,如图是她离家的距离与所用时间的关系示意图,请根据图中提供的信息回答下列问题:
(1
)小颖家与学校的距离是多少米?
(2
)点
A
表示的实际意义是什么?
(3
)小颖本次从学校回家的整个过程中,走过的路程是多少米?
(4
)买到彩笔后,小颖从文具用品店回到家步行的速度是多少米
/
分?
)
1
6
