2023-2024学年河南省信阳市罗山县七年级(下)期末数学试卷(含答案)
文档属性
| 名称 | 2023-2024学年河南省信阳市罗山县七年级(下)期末数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 142.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-29 00:00:00 | ||
图片预览



文档简介
2023-2024学年河南省信阳市罗山县七年级(下)期末数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.的平方根是( )
A. B. C. D.
2.空气的成分除去水汽、杂质等是:氮气约占,氧气约占,其他微量气体约占要反映上述信息,宜采用的统计图是( )
A. 条形统计图 B. 折线统计图 C. 扇形统计图 D. 频数分布直方图
3.故宫旧称紫禁城,是世界现存最大、最完整的古建筑群,被誉为世界五大宫之首故宫太和门庭院的长宽比满足黄金分割比,所以看起来赏心悦目,请你估算的值在( )
A. 到之间 B. 到之间 C. 到之间 D. 到之间
4.一瓶牛奶的营养成分中,碳水化合物含量是蛋白质的倍,碳水化合物、蛋白质与脂肪的含量共设蛋白质、脂肪的含量分别为,,可列出方程为( )
A. B. C. D.
5.如图,将一把直尺与一块三角板按图中所示位置放置,若,则的度数为( )
A.
B.
C.
D.
6.如图是测量一颗玻璃球体积的过程:
将的水倒进一个容量为的杯子中;
将四颗相同的玻璃球放入水中,结果水没有满;
再将一颗同样的玻璃球放入水中,结果水满溢出.
根据以上过程,推测一颗玻璃球的体积( )
A. 大于,小于 B. 大于,小于
C. 大于,小于 D. 大于,小于
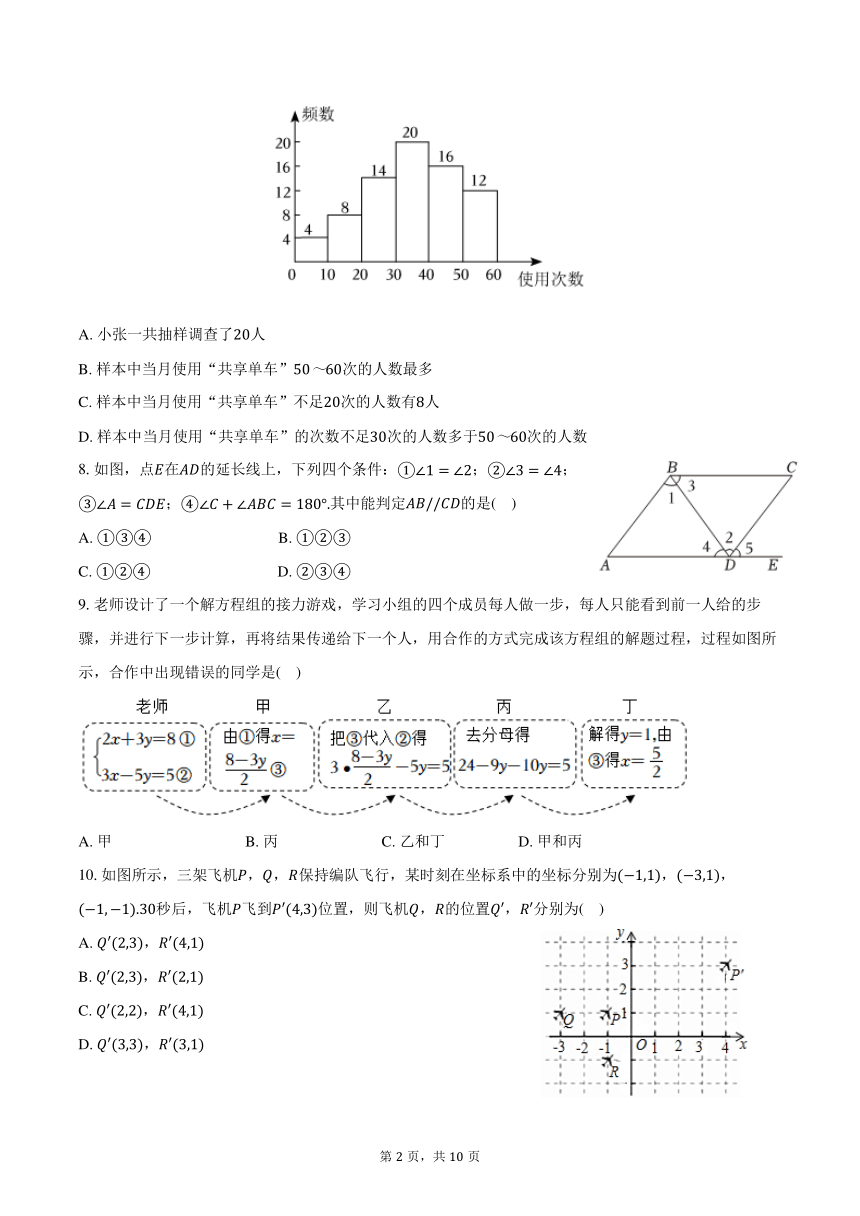
7.“共享单车”为人们提供了一种经济便捷、绿色低碳的共享服务,成为城市交通出行的新方式,小张对他所在小区居民当月使用“共享单车”的次数进行了抽样调查,并绘制成了如图所示的频数分布直方图每一组含前一个边界值,不含后一个边界值,则下列说法正确的是( )
A. 小张一共抽样调查了人
B. 样本中当月使用“共享单车”次的人数最多
C. 样本中当月使用“共享单车”不足次的人数有人
D. 样本中当月使用“共享单车”的次数不足次的人数多于次的人数
8.如图,点在的延长线上,下列四个条件:;;
;其中能判定的是( )
A. B.
C. D.
9.老师设计了一个解方程组的接力游戏,学习小组的四个成员每人做一步,每人只能看到前一人给的步骤,并进行下一步计算,再将结果传递给下一个人,用合作的方式完成该方程组的解题过程,过程如图所示,合作中出现错误的同学是( )
A. 甲 B. 丙 C. 乙和丁 D. 甲和丙
10.如图所示,三架飞机,,保持编队飞行,某时刻在坐标系中的坐标分别为,,秒后,飞机飞到位置,则飞机,的位置,分别为( )
A. ,
B. ,
C. ,
D. ,
二、填空题:本题共5小题,每小题3分,共15分。
11.若,则 ______.
12.小亮对名同学进行节水方法选择的问卷调查每人选择一项,人数统计如图,如果绘制成扇形统计图,那么表示“一水多用”的扇形圆心角的度数是______.
13.不等式的最小整数解是______.
14.为响应国家新能源建设,乐清市公交站亭装上了太阳能电池板当地某一季节的太阳光平行光线与水平线最大夹角为,如图,电池板与最大夹角时刻的太阳光线相垂直,此时电池板与水平线夹角为,要使,需将电池板逆时针旋转度,则为______.
15.如图,在平面直角坐标系中,点在轴上,点,线段向右平移个单位至
线段,线段与轴交于点,若图中阴影部分面积是,则点的坐标为_____.
三、解答题:本题共8小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
计算:
;
.
17.本小题分
解不等式组分并将解集表示在数轴上.
18.本小题分
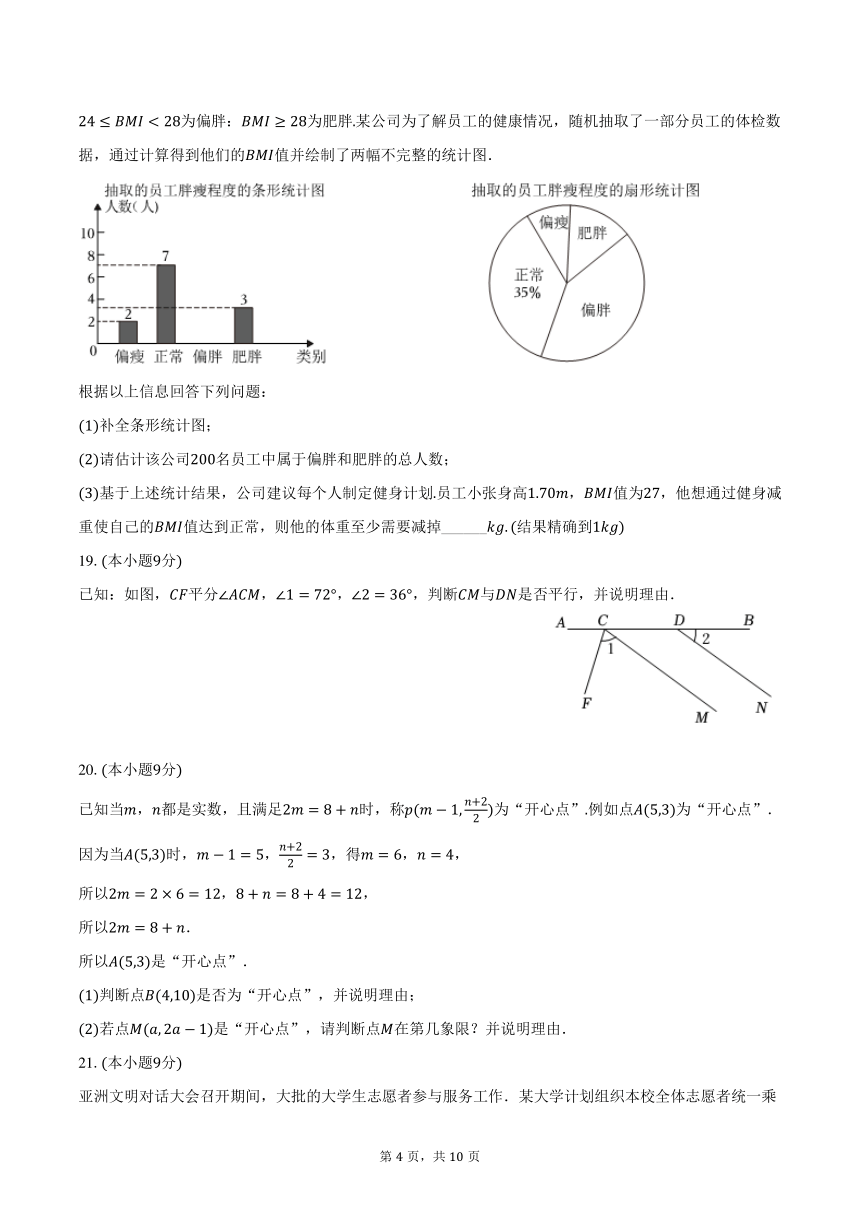
近年来,肥胖已经成为影响人们身体健康的重要因素,国际上常身体质量指数,缩写来衡量人体程度以及是否康其计算公式是,例如:某人身高,体重,则他的,中国成人的数值标准为:为偏瘦;为正常;为偏胖:为肥胖某公司为了解员工的健康情况,随机抽取了一部分员工的体检数据,通过计算得到他们的值并绘制了两幅不完整的统计图.
根据以上信息回答下列问题:
补全条形统计图;
请估计该公司名员工中属于偏胖和肥胖的总人数;
基于上述统计结果,公司建议每个人制定健身计划员工小张身高,值为,他想通过健身减重使自己的值达到正常,则他的体重至少需要减掉______结果精确到
19.本小题分
已知:如图,平分,,,判断与是否平行,并说明理由.
20.本小题分
已知当,都是实数,且满足时,称为“开心点”例如点为“开心点”.
因为当时,,,得,,
所以,,
所以.
所以是“开心点”.
判断点是否为“开心点”,并说明理由;
若点是“开心点”,请判断点在第几象限?并说明理由.
21.本小题分
亚洲文明对话大会召开期间,大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场,若单独调配座新能源客车若干辆,则有人没有座位;若只调配座新能源客车,则用车数量将增加辆,并空出个座位.
计划调配座新能源客车多少辆?该大学共有多少名志愿者?
若同时调配座和座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?
22.本小题分
为了促进消费,端午节期间,甲,乙两家商场以同样的价格出售同样的商品,并且又各自推出不同的促销方案.
甲商场的优惠方案:购物价格累计超过元后,超出元的部分按付费;
乙商场的优惠方案:购物价格累计超过元后,超出元的部分按付费;
七年级数学试题第页共页
若某顾客准备购买标价为元的商品.
在甲商场购买的优惠价为______元,在乙商场购买的优惠价为______元均用含的式子表示;
该顾客到哪家商场购物花费少?写出解答过程;
23.本小题分
如图,直线,点在两平行线之间,点在上,点在上,连接,.
若,,则的度数为______
如图,若点,在直线与之间,,,,则的度数为______
如图,在图基础上,作平分,平分,若设,,则 ______
如图,若平分,平分,可得,平分,平分,可得,,依次平分下去,则 ______用含,的式子表示
在一次综合实践活动课上,张开同学制作了一个如图所示的“回旋镖”,经测量发现,,他很想知道与的数量关系,你能告诉他吗?请你写出求解过程.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.解:
;
.
17.解:,
解不等式,得,
解不等式,得,
不等式组的解集为,
将不等式组的解集表示在数轴上如图.
.
18.解:人,
偏胖人数:人,
条形图如下:
;
人,
答:公司名员工中属于偏胖和肥胖的总人数人;
.
19.解:,理由为:
平分,
,
,
,
,
,
,
.
20.解:不是“开心点”,理由如下,
当时,,,
解得,,
则,,
所以,
所以点不是“开心点”.
点在第三象限,理由如下:
因为点是“开心点”,
所以,,
所以,,
代入,有,
所以,
所以,
所以,
故点在第三象限.
21.解:设计划调配座新能源客车辆,该大学共有名志愿者,则需调配座新能源客车辆,
依题意,得:,
解得:.
答:计划调配座新能源客车辆,该大学共有名志愿者.
设需调配座客车辆,座客车辆,
依题意,得:,
.
又,均为正整数,
.
答:需调配座客车辆,座客车辆.
22.:;.
当顾客在甲商场购物花费少时:,解得:;
当顾客在乙商场购物花费少时:,解得:;
当顾客在甲、乙商场购物花费相等时:,解得:;
当时,顾客在甲商场购物花费少;
当时,顾客在甲、乙商场购物花费相同;
当时,顾客在乙商场购物花费少.
23..
.
;.
过点作交于点,如图所示,
,,
,,
,
,,
,
第1页,共1页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.的平方根是( )
A. B. C. D.
2.空气的成分除去水汽、杂质等是:氮气约占,氧气约占,其他微量气体约占要反映上述信息,宜采用的统计图是( )
A. 条形统计图 B. 折线统计图 C. 扇形统计图 D. 频数分布直方图
3.故宫旧称紫禁城,是世界现存最大、最完整的古建筑群,被誉为世界五大宫之首故宫太和门庭院的长宽比满足黄金分割比,所以看起来赏心悦目,请你估算的值在( )
A. 到之间 B. 到之间 C. 到之间 D. 到之间
4.一瓶牛奶的营养成分中,碳水化合物含量是蛋白质的倍,碳水化合物、蛋白质与脂肪的含量共设蛋白质、脂肪的含量分别为,,可列出方程为( )
A. B. C. D.
5.如图,将一把直尺与一块三角板按图中所示位置放置,若,则的度数为( )
A.
B.
C.
D.
6.如图是测量一颗玻璃球体积的过程:
将的水倒进一个容量为的杯子中;
将四颗相同的玻璃球放入水中,结果水没有满;
再将一颗同样的玻璃球放入水中,结果水满溢出.
根据以上过程,推测一颗玻璃球的体积( )
A. 大于,小于 B. 大于,小于
C. 大于,小于 D. 大于,小于
7.“共享单车”为人们提供了一种经济便捷、绿色低碳的共享服务,成为城市交通出行的新方式,小张对他所在小区居民当月使用“共享单车”的次数进行了抽样调查,并绘制成了如图所示的频数分布直方图每一组含前一个边界值,不含后一个边界值,则下列说法正确的是( )
A. 小张一共抽样调查了人
B. 样本中当月使用“共享单车”次的人数最多
C. 样本中当月使用“共享单车”不足次的人数有人
D. 样本中当月使用“共享单车”的次数不足次的人数多于次的人数
8.如图,点在的延长线上,下列四个条件:;;
;其中能判定的是( )
A. B.
C. D.
9.老师设计了一个解方程组的接力游戏,学习小组的四个成员每人做一步,每人只能看到前一人给的步骤,并进行下一步计算,再将结果传递给下一个人,用合作的方式完成该方程组的解题过程,过程如图所示,合作中出现错误的同学是( )
A. 甲 B. 丙 C. 乙和丁 D. 甲和丙
10.如图所示,三架飞机,,保持编队飞行,某时刻在坐标系中的坐标分别为,,秒后,飞机飞到位置,则飞机,的位置,分别为( )
A. ,
B. ,
C. ,
D. ,
二、填空题:本题共5小题,每小题3分,共15分。
11.若,则 ______.
12.小亮对名同学进行节水方法选择的问卷调查每人选择一项,人数统计如图,如果绘制成扇形统计图,那么表示“一水多用”的扇形圆心角的度数是______.
13.不等式的最小整数解是______.
14.为响应国家新能源建设,乐清市公交站亭装上了太阳能电池板当地某一季节的太阳光平行光线与水平线最大夹角为,如图,电池板与最大夹角时刻的太阳光线相垂直,此时电池板与水平线夹角为,要使,需将电池板逆时针旋转度,则为______.
15.如图,在平面直角坐标系中,点在轴上,点,线段向右平移个单位至
线段,线段与轴交于点,若图中阴影部分面积是,则点的坐标为_____.
三、解答题:本题共8小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
计算:
;
.
17.本小题分
解不等式组分并将解集表示在数轴上.
18.本小题分
近年来,肥胖已经成为影响人们身体健康的重要因素,国际上常身体质量指数,缩写来衡量人体程度以及是否康其计算公式是,例如:某人身高,体重,则他的,中国成人的数值标准为:为偏瘦;为正常;为偏胖:为肥胖某公司为了解员工的健康情况,随机抽取了一部分员工的体检数据,通过计算得到他们的值并绘制了两幅不完整的统计图.
根据以上信息回答下列问题:
补全条形统计图;
请估计该公司名员工中属于偏胖和肥胖的总人数;
基于上述统计结果,公司建议每个人制定健身计划员工小张身高,值为,他想通过健身减重使自己的值达到正常,则他的体重至少需要减掉______结果精确到
19.本小题分
已知:如图,平分,,,判断与是否平行,并说明理由.
20.本小题分
已知当,都是实数,且满足时,称为“开心点”例如点为“开心点”.
因为当时,,,得,,
所以,,
所以.
所以是“开心点”.
判断点是否为“开心点”,并说明理由;
若点是“开心点”,请判断点在第几象限?并说明理由.
21.本小题分
亚洲文明对话大会召开期间,大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场,若单独调配座新能源客车若干辆,则有人没有座位;若只调配座新能源客车,则用车数量将增加辆,并空出个座位.
计划调配座新能源客车多少辆?该大学共有多少名志愿者?
若同时调配座和座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?
22.本小题分
为了促进消费,端午节期间,甲,乙两家商场以同样的价格出售同样的商品,并且又各自推出不同的促销方案.
甲商场的优惠方案:购物价格累计超过元后,超出元的部分按付费;
乙商场的优惠方案:购物价格累计超过元后,超出元的部分按付费;
七年级数学试题第页共页
若某顾客准备购买标价为元的商品.
在甲商场购买的优惠价为______元,在乙商场购买的优惠价为______元均用含的式子表示;
该顾客到哪家商场购物花费少?写出解答过程;
23.本小题分
如图,直线,点在两平行线之间,点在上,点在上,连接,.
若,,则的度数为______
如图,若点,在直线与之间,,,,则的度数为______
如图,在图基础上,作平分,平分,若设,,则 ______
如图,若平分,平分,可得,平分,平分,可得,,依次平分下去,则 ______用含,的式子表示
在一次综合实践活动课上,张开同学制作了一个如图所示的“回旋镖”,经测量发现,,他很想知道与的数量关系,你能告诉他吗?请你写出求解过程.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.解:
;
.
17.解:,
解不等式,得,
解不等式,得,
不等式组的解集为,
将不等式组的解集表示在数轴上如图.
.
18.解:人,
偏胖人数:人,
条形图如下:
;
人,
答:公司名员工中属于偏胖和肥胖的总人数人;
.
19.解:,理由为:
平分,
,
,
,
,
,
,
.
20.解:不是“开心点”,理由如下,
当时,,,
解得,,
则,,
所以,
所以点不是“开心点”.
点在第三象限,理由如下:
因为点是“开心点”,
所以,,
所以,,
代入,有,
所以,
所以,
所以,
故点在第三象限.
21.解:设计划调配座新能源客车辆,该大学共有名志愿者,则需调配座新能源客车辆,
依题意,得:,
解得:.
答:计划调配座新能源客车辆,该大学共有名志愿者.
设需调配座客车辆,座客车辆,
依题意,得:,
.
又,均为正整数,
.
答:需调配座客车辆,座客车辆.
22.:;.
当顾客在甲商场购物花费少时:,解得:;
当顾客在乙商场购物花费少时:,解得:;
当顾客在甲、乙商场购物花费相等时:,解得:;
当时,顾客在甲商场购物花费少;
当时,顾客在甲、乙商场购物花费相同;
当时,顾客在乙商场购物花费少.
23..
.
;.
过点作交于点,如图所示,
,,
,,
,
,,
,
第1页,共1页
同课章节目录
