2023-2024学年山东省德州市临邑县七年级(下)期末数学试卷(含答案)
文档属性
| 名称 | 2023-2024学年山东省德州市临邑县七年级(下)期末数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 102.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-29 00:00:00 | ||
图片预览




文档简介
2023-2024学年山东省德州市临邑县七年级(下)期末数学试卷
一、选择题:本题共12小题,每小题4分,共48分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列实数是无理数的是( )
A. B. C. D.
2.判断下列命题是假命题的是( )
A. 对顶角相等 B. 邻补角是互补的角
C. 同旁内角互补 D. 正方形的四个角都是直角
3.为了解某校七年级名学生对“创建全国文明校园”知识的了解情况,学校组织了相关知识测试,并从中随机抽取了名学生的成绩进行统计分析,下列说法正确的是( )
A. 名学生是总体 B. 本校七年级每名学生的测试成绩是个体
C. 样本容量是 D. 被抽取的名学生是样本
4.若,则下列不等式中错误的是( )
A. B. C. D.
5.在解二元一次方程组时,下列方法中无法消元的是( )
A.
B. 由变形得,将代入
C.
D. 由变形得,将代入
6.如图,,,,则等于( )
A.
B.
C.
D.
7.如果方程组的解与方程组的解相同,则的值为( )
A. B. C. D.
8.如果点是第二象限的点,则的取值范围在数轴上表示正确的是( )
A. B.
C. D.
9.我国古代数学名著算法统宗中记载:“今有绫七尺,罗九尺,共价适等;只云罗每尺价比绫每尺少钱三十六文,问各钱价若干?”意思是:现在有一匹尺长的绫布和一匹尺长的罗布恰好一样贵,只知道每尺罗布比绫布便宜文,问两种布每尺各多少钱?设绫布每尺文,罗布每尺文,那么可列方程组为( )
A. B. C. D.
10.如图,在平面直角坐标系中,长方形的边与轴平行且,,点坐标为,沿某一方向平移后,点的对应点的坐标为,则点的坐标为( )
A.
B.
C.
D.
11.关于的不等式组有四个整数解,则的取值范围是( )
A. B. C. D.
12.如图,,的平分线相交于,过点作,交于,交于,那么下列结论中:;;;的周长,其中正确的有几个( )
A. 个 B. 个 C. 个 D. 个
二、填空题:本题共6小题,每小题4分,共24分。
13. ______, ______.
14.如图,一个含有角的直角三角尺的两个顶点放在直尺的对边上.
如果,那么的度数是______.
15.已知点,点关于轴对称,则的值是______.
16.随机抽取一批毛衫的合格情况,得到如下的频数表.
抽取件数件
合格频数
合格频率
估计出厂的件毛衫中,次品大约有______件
17.如图,一处长方形展览大厅内,修建了宽为米的通道,其余部分
摆放展品,则可供摆放展品的面积为______平方米.
18.定义一种法则“”如下:,如:,
若,则的取值范围是______.
三、解答题:本题共7小题,共78分。解答应写出文字说明,证明过程或演算步骤。
19.本小题分
如图,已知点,在直线上,点在线段上,与交于点,,.
求证:.
若,,求的度数.
20.本小题分
计算
已知一个整数的两个平方根分别为和,是的整数部分,求的立方根.
解不等式组:,并将解集在数轴上表示出来.
21.本小题分
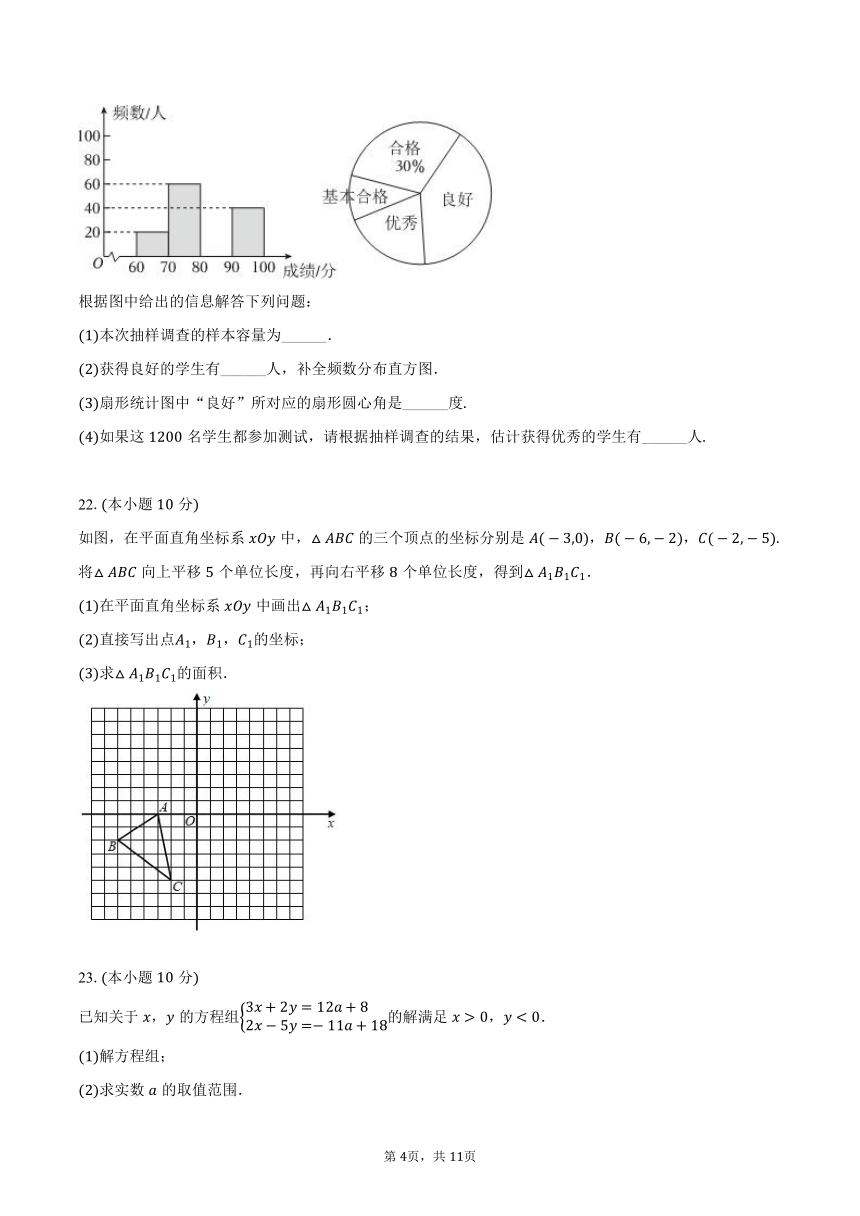
为了解校园安全知识在学校的普及情况,实验中学从名学生中随机抽取部分学生进行校园安全知识测试测试满分分,得分均为不小于的整数,并将测试成绩分为四个等级:基本合格,合格,良好,优秀,整理后将结果绘制成不完整的统计图如下.
根据图中给出的信息解答下列问题:
本次抽样调查的样本容量为______.
获得良好的学生有______人,补全频数分布直方图.
扇形统计图中“良好”所对应的扇形圆心角是______度
如果这名学生都参加测试,请根据抽样调查的结果,估计获得优秀的学生有______人
22.本小题分
如图,在平面直角坐标系中,的三个顶点的坐标分别是,,将向上平移个单位长度,再向右平移个单位长度,得到.
在平面直角坐标系中画出;
直接写出点,,的坐标;
求的面积.
23.本小题分
已知关于,的方程组的解满足,.
解方程组;
求实数的取值范围.
24.本小题分
某商场销售,两种品牌的多媒体教学设备,这两种多媒体教学设备的进价和售价如表所示
进价万元套
售价万元套
若该商场计划购进两种多媒体教学设备若干套,共需万元,全部销售后可获毛利润万元.则该商场计划购进,两种品牌的多媒体教学设备各多少套?
通过市场调研,该商场决定在中所购总数量不变的基础上,减少种设备的购进数量,增加种设备的购进数量.若用于购进这两种多媒体教学设备的总资金不超过万元,且全部销售后可获毛利润不少于万元.问有几种购买方案?并写出购买方案.
25.本小题分
【阅读理解】
我们经常过某个点作已知直线的平行线,以便利用平行线的性质来解决问题.
例如:如图,,点、分别在直线、上,点在直线、之间,设,,求证:.
证明:如图,过点作,
,
,,
,
,
.
即.
可以运用以上结论解答下列问题:
【类比应用】
如图,已知,已知,,求的度数;
如图,已知,点在直线上,点在直线上方,连接、设、,则、、之间有何数量关系?请说明理由;
【拓展应用】
如图,已知,点在直线上,点在直线上方,连接、,的角平分线与的角平分线所在直线交于点,求的度数.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.证明:,
,
,
,
;
解:,,
,
,
,
由知,
.
答:的度数为.
20.解:一个整数的两个平方根分别为和,
,
,
又是的整数部分,且,
,
,
的立方根是;
解不等式:
,
,
,
,
;
解不等式:
,
,
,
,
,
;
不等式组的解集为,
将解集在数轴上如下:
21.
【解析】解:;
获得良好的学生有:人,
补全频数分布直方图如下:
;
.
22.解:如图,即为所求;
,,;
的面积.
23.解:,
得:;
把代入得:,
方程组的解为;
,,
,
解得:.
24.解:设该商场计划购进种设备套,种设备套,
依题意,得:,
解得:.
答:该商场计划购进种设备套,种设备套.
设该商场购进种设备套,则购进种设备套,
依题意,得:,
解得:.
为正整数,
,或.
有三种购买方案,方案一:购进种设备套、种设备套;方案二:购进种设备套、种设备套;方案三:购进种设备套、种设备套.
25.解:如图,过点作,
,
,,
,
,
,
即.
,理由如下:
如图,过点作,
,
,
,
,,
,
,
,
即.
设,,
平分,平分,
,,
,
由可知,,
由材料的结论可知,,
.
第1页,共1页
一、选择题:本题共12小题,每小题4分,共48分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列实数是无理数的是( )
A. B. C. D.
2.判断下列命题是假命题的是( )
A. 对顶角相等 B. 邻补角是互补的角
C. 同旁内角互补 D. 正方形的四个角都是直角
3.为了解某校七年级名学生对“创建全国文明校园”知识的了解情况,学校组织了相关知识测试,并从中随机抽取了名学生的成绩进行统计分析,下列说法正确的是( )
A. 名学生是总体 B. 本校七年级每名学生的测试成绩是个体
C. 样本容量是 D. 被抽取的名学生是样本
4.若,则下列不等式中错误的是( )
A. B. C. D.
5.在解二元一次方程组时,下列方法中无法消元的是( )
A.
B. 由变形得,将代入
C.
D. 由变形得,将代入
6.如图,,,,则等于( )
A.
B.
C.
D.
7.如果方程组的解与方程组的解相同,则的值为( )
A. B. C. D.
8.如果点是第二象限的点,则的取值范围在数轴上表示正确的是( )
A. B.
C. D.
9.我国古代数学名著算法统宗中记载:“今有绫七尺,罗九尺,共价适等;只云罗每尺价比绫每尺少钱三十六文,问各钱价若干?”意思是:现在有一匹尺长的绫布和一匹尺长的罗布恰好一样贵,只知道每尺罗布比绫布便宜文,问两种布每尺各多少钱?设绫布每尺文,罗布每尺文,那么可列方程组为( )
A. B. C. D.
10.如图,在平面直角坐标系中,长方形的边与轴平行且,,点坐标为,沿某一方向平移后,点的对应点的坐标为,则点的坐标为( )
A.
B.
C.
D.
11.关于的不等式组有四个整数解,则的取值范围是( )
A. B. C. D.
12.如图,,的平分线相交于,过点作,交于,交于,那么下列结论中:;;;的周长,其中正确的有几个( )
A. 个 B. 个 C. 个 D. 个
二、填空题:本题共6小题,每小题4分,共24分。
13. ______, ______.
14.如图,一个含有角的直角三角尺的两个顶点放在直尺的对边上.
如果,那么的度数是______.
15.已知点,点关于轴对称,则的值是______.
16.随机抽取一批毛衫的合格情况,得到如下的频数表.
抽取件数件
合格频数
合格频率
估计出厂的件毛衫中,次品大约有______件
17.如图,一处长方形展览大厅内,修建了宽为米的通道,其余部分
摆放展品,则可供摆放展品的面积为______平方米.
18.定义一种法则“”如下:,如:,
若,则的取值范围是______.
三、解答题:本题共7小题,共78分。解答应写出文字说明,证明过程或演算步骤。
19.本小题分
如图,已知点,在直线上,点在线段上,与交于点,,.
求证:.
若,,求的度数.
20.本小题分
计算
已知一个整数的两个平方根分别为和,是的整数部分,求的立方根.
解不等式组:,并将解集在数轴上表示出来.
21.本小题分
为了解校园安全知识在学校的普及情况,实验中学从名学生中随机抽取部分学生进行校园安全知识测试测试满分分,得分均为不小于的整数,并将测试成绩分为四个等级:基本合格,合格,良好,优秀,整理后将结果绘制成不完整的统计图如下.
根据图中给出的信息解答下列问题:
本次抽样调查的样本容量为______.
获得良好的学生有______人,补全频数分布直方图.
扇形统计图中“良好”所对应的扇形圆心角是______度
如果这名学生都参加测试,请根据抽样调查的结果,估计获得优秀的学生有______人
22.本小题分
如图,在平面直角坐标系中,的三个顶点的坐标分别是,,将向上平移个单位长度,再向右平移个单位长度,得到.
在平面直角坐标系中画出;
直接写出点,,的坐标;
求的面积.
23.本小题分
已知关于,的方程组的解满足,.
解方程组;
求实数的取值范围.
24.本小题分
某商场销售,两种品牌的多媒体教学设备,这两种多媒体教学设备的进价和售价如表所示
进价万元套
售价万元套
若该商场计划购进两种多媒体教学设备若干套,共需万元,全部销售后可获毛利润万元.则该商场计划购进,两种品牌的多媒体教学设备各多少套?
通过市场调研,该商场决定在中所购总数量不变的基础上,减少种设备的购进数量,增加种设备的购进数量.若用于购进这两种多媒体教学设备的总资金不超过万元,且全部销售后可获毛利润不少于万元.问有几种购买方案?并写出购买方案.
25.本小题分
【阅读理解】
我们经常过某个点作已知直线的平行线,以便利用平行线的性质来解决问题.
例如:如图,,点、分别在直线、上,点在直线、之间,设,,求证:.
证明:如图,过点作,
,
,,
,
,
.
即.
可以运用以上结论解答下列问题:
【类比应用】
如图,已知,已知,,求的度数;
如图,已知,点在直线上,点在直线上方,连接、设、,则、、之间有何数量关系?请说明理由;
【拓展应用】
如图,已知,点在直线上,点在直线上方,连接、,的角平分线与的角平分线所在直线交于点,求的度数.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.证明:,
,
,
,
;
解:,,
,
,
,
由知,
.
答:的度数为.
20.解:一个整数的两个平方根分别为和,
,
,
又是的整数部分,且,
,
,
的立方根是;
解不等式:
,
,
,
,
;
解不等式:
,
,
,
,
,
;
不等式组的解集为,
将解集在数轴上如下:
21.
【解析】解:;
获得良好的学生有:人,
补全频数分布直方图如下:
;
.
22.解:如图,即为所求;
,,;
的面积.
23.解:,
得:;
把代入得:,
方程组的解为;
,,
,
解得:.
24.解:设该商场计划购进种设备套,种设备套,
依题意,得:,
解得:.
答:该商场计划购进种设备套,种设备套.
设该商场购进种设备套,则购进种设备套,
依题意,得:,
解得:.
为正整数,
,或.
有三种购买方案,方案一:购进种设备套、种设备套;方案二:购进种设备套、种设备套;方案三:购进种设备套、种设备套.
25.解:如图,过点作,
,
,,
,
,
,
即.
,理由如下:
如图,过点作,
,
,
,
,,
,
,
,
即.
设,,
平分,平分,
,,
,
由可知,,
由材料的结论可知,,
.
第1页,共1页
同课章节目录
