【人教九上中档题专题提优】专题六 二次函数与判别式(2)—几何求参(含解析)
文档属性
| 名称 | 【人教九上中档题专题提优】专题六 二次函数与判别式(2)—几何求参(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 231.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-30 09:38:02 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
专题六 二次函数与判别式(2)—几何求参
核心考点一 根据图象的临界位置,利用判别式求参数范围
01.如图,抛物线y=-2x2+8x-6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,求m的取值范围.
核心考点二 根据图形的唯一存在性,利用判别式求参数范围
02. 在平面直角坐标系中,抛物线y=x2+(k-1)x-k与直线y=kx+1交于A,B两点,点A在点B的左侧,设抛物线与x轴交于C,D两点(点C在点D的左侧).在直线y=kx+1上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时k的值;若不存在,请说明理由.
核心考点三 根据图形的恒存在性,利用判别式求参数范围
03. 如图,点P是直线l:y=-2x-2上的点,过点P的另一条直线m交抛物线y=x2于A、B两点,试证明:对于直线l上任意给定的一点P,在抛物线上都能找到点A,使得PA=AB成立.
专题六 二次函数与判别式(2)—几何求参
核心考点一 根据图象的临界位置,利用判别式求参数范围
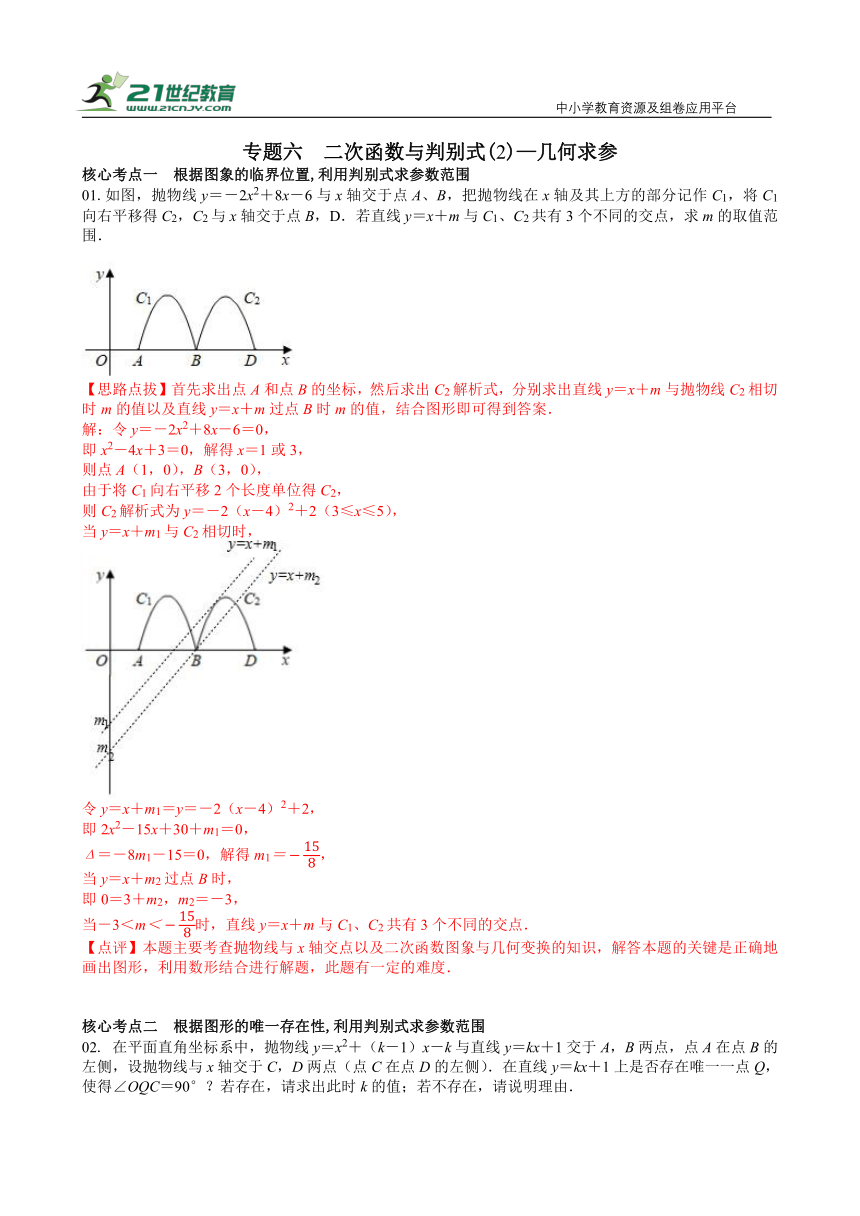
01.如图,抛物线y=-2x2+8x-6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,求m的取值范围.
【思路点拔】首先求出点A和点B的坐标,然后求出C2解析式,分别求出直线y=x+m与抛物线C2相切时m的值以及直线y=x+m过点B时m的值,结合图形即可得到答案.
解:令y=-2x2+8x-6=0,
即x2-4x+3=0,解得x=1或3,
则点A(1,0),B(3,0),
由于将C1向右平移2个长度单位得C2,
则C2解析式为y=-2(x-4)2+2(3≤x≤5),
当y=x+m1与C2相切时,
令y=x+m1=y=-2(x-4)2+2,
即2x2-15x+30+m1=0,
Δ=-8m1-15=0,解得m1,
当y=x+m2过点B时,
即0=3+m2,m2=-3,
当-3<m时,直线y=x+m与C1、C2共有3个不同的交点.
【点评】本题主要考查抛物线与x轴交点以及二次函数图象与几何变换的知识,解答本题的关键是正确地画出图形,利用数形结合进行解题,此题有一定的难度.
核心考点二 根据图形的唯一存在性,利用判别式求参数范围
02. 在平面直角坐标系中,抛物线y=x2+(k-1)x-k与直线y=kx+1交于A,B两点,点A在点B的左侧,设抛物线与x轴交于C,D两点(点C在点D的左侧).在直线y=kx+1上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时k的值;若不存在,请说明理由.
【思路点拔】“存在唯一一点Q,使得∠OQC=90°”的含义是,以OC为直径的圆与直线AB相切于点Q,由圆周角定理可知,此时∠OQC=90°且点Q为唯一.以此为基础,构造相似三角形,利用比例式列出方程,求得k的值.需要另外注意一点是考虑直线AB是否与抛物线交于C点,此时亦存在唯一一点Q,使得∠OQC=90°.
【解答】解:以CO为直径,作⊙M,
当直线AB与⊙M相切时,
此时在直线y=kx+1上存在唯一一点Q,使得∠OQC=90°,且切点为Q,
连接QM,则MQ⊥AB,如图1,
当直线AB与⊙M相切时,
设直线AB:y=kx+1与x轴、y轴分别交于点E、F,
则E(,0),F(0,1),OE,OF=1.
在Rt△EOF中,由勾股定理得:EF.
令y=x2+(k-1)x-k=0,即(x+k)(x-1)=0,
解得:x=-k或x=1.
∴C(-k,0),OC=k,
∴MC=MO=MQ,
∴EM,
∵∠EQM=∠EOF=90°,∠MEQ=∠FEO,
∴,即,
解得:k=±,
由图象可知k>0,
∴k.
当直线AB与⊙M相交于时,
若在直线y=kx+1上是否存在唯一一点Q,使得∠OQC=90°,
则直线AB必过点C,即A与C重合如图2:
∵OC=k,OA,
∴k,∴k=1,
综上所述:k=1或k.
【点评】本题考查二次函数的综合问题,涉及相似三角形的判定与性质,圆周角定理,勾股定理等知识,内容较为综合,知识点较多,需要学生灵活运用所学知识进行解答.
核心考点三 根据图形的恒存在性,利用判别式求参数范围
03. 如图,点P是直线l:y=-2x-2上的点,过点P的另一条直线m交抛物线y=x2于A、B两点,试证明:对于直线l上任意给定的一点P,在抛物线上都能找到点A,使得PA=AB成立.
【思路点拔】首先设P(a,-2a-2),A(m,m2),再表示出B点坐标,进而利用根的判别式求出,无论a为何值时,关于m的方程总有两个不相等的实数根,进而得出答案.
【解答】证明:设P(a,-2a-2),A(m,m2).
如图所示,
分别过点P、A、B作x轴的垂线,垂足分别为点G、E、F.
∵PA=AB,∴AE是梯形PGFB的中位线,
∴GE=EF,AE(PG+BF).
∵OF=|EF-OE|,GE=EF,
∴OF=|GE-EO|
∵GE=GO-EO=m-a,EO=-m,
∴OF=|m-a-(-m)|=|2m-a|,
∴OF=2m-a,
∵AE(PG+BF),
∴BF=2AE-PG=2m2+2a+2,
可得:B(2m-a,2m2+2a+2).
∵点B在抛物线y=x2上,
∴2m2+2a+2=(2m-a)2
整理得:2m2-4am+a2-2a-2=0.
Δ=8(a+1)2+8>0,
∴无论a为何值时,关于m的方程总有两个不相等的实数根.
即对于任意给定的点P,抛物线上总能找到满足条件的点A,使得PA=AB成立.
【点评】本题考查二次函数与一次函数的图象与性质、梯形及梯形中位线、一元二次方程等知识点,掌握二次函数、一次函数点的坐标特征,正确表示出B点坐标是解题关键.
专题六 二次函数与判别式(2)—几何求参
核心考点一 根据图象的临界位置,利用判别式求参数范围
01.如图,抛物线y=-2x2+8x-6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,求m的取值范围.
核心考点二 根据图形的唯一存在性,利用判别式求参数范围
02. 在平面直角坐标系中,抛物线y=x2+(k-1)x-k与直线y=kx+1交于A,B两点,点A在点B的左侧,设抛物线与x轴交于C,D两点(点C在点D的左侧).在直线y=kx+1上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时k的值;若不存在,请说明理由.
核心考点三 根据图形的恒存在性,利用判别式求参数范围
03. 如图,点P是直线l:y=-2x-2上的点,过点P的另一条直线m交抛物线y=x2于A、B两点,试证明:对于直线l上任意给定的一点P,在抛物线上都能找到点A,使得PA=AB成立.
专题六 二次函数与判别式(2)—几何求参
核心考点一 根据图象的临界位置,利用判别式求参数范围
01.如图,抛物线y=-2x2+8x-6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,求m的取值范围.
【思路点拔】首先求出点A和点B的坐标,然后求出C2解析式,分别求出直线y=x+m与抛物线C2相切时m的值以及直线y=x+m过点B时m的值,结合图形即可得到答案.
解:令y=-2x2+8x-6=0,
即x2-4x+3=0,解得x=1或3,
则点A(1,0),B(3,0),
由于将C1向右平移2个长度单位得C2,
则C2解析式为y=-2(x-4)2+2(3≤x≤5),
当y=x+m1与C2相切时,
令y=x+m1=y=-2(x-4)2+2,
即2x2-15x+30+m1=0,
Δ=-8m1-15=0,解得m1,
当y=x+m2过点B时,
即0=3+m2,m2=-3,
当-3<m时,直线y=x+m与C1、C2共有3个不同的交点.
【点评】本题主要考查抛物线与x轴交点以及二次函数图象与几何变换的知识,解答本题的关键是正确地画出图形,利用数形结合进行解题,此题有一定的难度.
核心考点二 根据图形的唯一存在性,利用判别式求参数范围
02. 在平面直角坐标系中,抛物线y=x2+(k-1)x-k与直线y=kx+1交于A,B两点,点A在点B的左侧,设抛物线与x轴交于C,D两点(点C在点D的左侧).在直线y=kx+1上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时k的值;若不存在,请说明理由.
【思路点拔】“存在唯一一点Q,使得∠OQC=90°”的含义是,以OC为直径的圆与直线AB相切于点Q,由圆周角定理可知,此时∠OQC=90°且点Q为唯一.以此为基础,构造相似三角形,利用比例式列出方程,求得k的值.需要另外注意一点是考虑直线AB是否与抛物线交于C点,此时亦存在唯一一点Q,使得∠OQC=90°.
【解答】解:以CO为直径,作⊙M,
当直线AB与⊙M相切时,
此时在直线y=kx+1上存在唯一一点Q,使得∠OQC=90°,且切点为Q,
连接QM,则MQ⊥AB,如图1,
当直线AB与⊙M相切时,
设直线AB:y=kx+1与x轴、y轴分别交于点E、F,
则E(,0),F(0,1),OE,OF=1.
在Rt△EOF中,由勾股定理得:EF.
令y=x2+(k-1)x-k=0,即(x+k)(x-1)=0,
解得:x=-k或x=1.
∴C(-k,0),OC=k,
∴MC=MO=MQ,
∴EM,
∵∠EQM=∠EOF=90°,∠MEQ=∠FEO,
∴,即,
解得:k=±,
由图象可知k>0,
∴k.
当直线AB与⊙M相交于时,
若在直线y=kx+1上是否存在唯一一点Q,使得∠OQC=90°,
则直线AB必过点C,即A与C重合如图2:
∵OC=k,OA,
∴k,∴k=1,
综上所述:k=1或k.
【点评】本题考查二次函数的综合问题,涉及相似三角形的判定与性质,圆周角定理,勾股定理等知识,内容较为综合,知识点较多,需要学生灵活运用所学知识进行解答.
核心考点三 根据图形的恒存在性,利用判别式求参数范围
03. 如图,点P是直线l:y=-2x-2上的点,过点P的另一条直线m交抛物线y=x2于A、B两点,试证明:对于直线l上任意给定的一点P,在抛物线上都能找到点A,使得PA=AB成立.
【思路点拔】首先设P(a,-2a-2),A(m,m2),再表示出B点坐标,进而利用根的判别式求出,无论a为何值时,关于m的方程总有两个不相等的实数根,进而得出答案.
【解答】证明:设P(a,-2a-2),A(m,m2).
如图所示,
分别过点P、A、B作x轴的垂线,垂足分别为点G、E、F.
∵PA=AB,∴AE是梯形PGFB的中位线,
∴GE=EF,AE(PG+BF).
∵OF=|EF-OE|,GE=EF,
∴OF=|GE-EO|
∵GE=GO-EO=m-a,EO=-m,
∴OF=|m-a-(-m)|=|2m-a|,
∴OF=2m-a,
∵AE(PG+BF),
∴BF=2AE-PG=2m2+2a+2,
可得:B(2m-a,2m2+2a+2).
∵点B在抛物线y=x2上,
∴2m2+2a+2=(2m-a)2
整理得:2m2-4am+a2-2a-2=0.
Δ=8(a+1)2+8>0,
∴无论a为何值时,关于m的方程总有两个不相等的实数根.
即对于任意给定的点P,抛物线上总能找到满足条件的点A,使得PA=AB成立.
【点评】本题考查二次函数与一次函数的图象与性质、梯形及梯形中位线、一元二次方程等知识点,掌握二次函数、一次函数点的坐标特征,正确表示出B点坐标是解题关键.
同课章节目录
