山东省德州市禹城市2023-2024学年八年级下学期期末考试数学试卷(含详细解答)
文档属性
| 名称 | 山东省德州市禹城市2023-2024学年八年级下学期期末考试数学试卷(含详细解答) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-29 00:00:00 | ||
图片预览




文档简介
山东省德州市禹城市2023-2024学年八年级下学期期末考试数学试卷
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列二次根式中,是最简二次根式的是( )
A. B. C. D.
2.中,,的对边分别记为a,b,c,下列条件不能判定为直角三角形的是( )
A. B.
C. D.
3.某射击小组有20人,教练根据他们某次射击的数据绘制成如图所示的统计图,则这组数据的众数和中位数分别是( )
A.7,7 B.8,7.5 C.7,7.5 D.8,6.5
4.下列有关一次函数的说法中,错误的是( )
A.y的值随着值的增大而减小 B.函数图象与轴的交点坐标为
C.当时 D.函数图象经过第一、二、四象限
5.如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若,,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是( )
A.72 B.52 C.80 D.76
6.已知点,点在一次函数的图像上,且,则m的取值范围是( )
A. B. C. D.
7.如图,要使平行四边形成为矩形,需添加的条件是( )
A. B. C. D.
8.如图,直线交坐标轴于,两点,则不等式的解集为( )
A. B. C. D.
9.如图,菱形的对角线,相交于点O.过点C作于点E.连接.若,,则的长为( )
A.2 B. C.6 D.8
10.A,B,C三种上宽带网方式的月收费金额(元),(元)(元)与月上网时间(小时)的对应关系如图所示,以下有四个推断:
①月上网时间不足35小时,选择方式A最省钱;
②月上网时间超过35小时且不足80小时,选择方式B最省线;
③对于上网方式B,若月上网时间在60小时以内,则月收费金额为60元;
④对于上网方式C,无论月上网时间是多久,月收费都是120元;
所有合理推断的序号是( )
A.①②③ B.①②③ C.②③④ D.①②③④
11.如图,在平面直角坐标系中,点A的坐标为,轴,轴,D是的中点,E是上的一点,当的周长最小时,点E的坐标是( )
A. B. C. D.
12.如图,在平行四边形中,对角线,相交于O,,E,F,G分别是,,的中点,下列结论:
①;②;③;④平分;⑤四边形是菱形.其中正确的是( )
A.①②③ B.①③④ C.①②⑤ D.②③⑤
二、填空题
13.若代数式有意义,则x的取值范围为______.
14.某校规定学生的数学学期综合成绩是由平时、期中和期末三项成绩按的比计算所得.若某同学本学期数学的平时、期中和期末成绩分别是80分、90分和95分,则他本学期数学学期综合成绩是______分.
15.如图,菱形的对角线,相交于点O,点P为边上一动点(不与点A,B重合),于点E,于点F.若,,则的最小值为______.
16.如图已知函数和的图象交于点P,点P的横坐标为1,则关于,y和x的方程组的解是______.
17.甲、乙两人在笔直的湖边公路上,同起点,同终点、同方向匀速步行2400米,先到终点的人原地休息,已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发时间(分钟)之间的关系如图所示,则乙到达终点时,甲离终点还有______米.
18.如图,已知在中,,点D是延长线上的一点,,点E是上一点,,连接,M,N分别是、的中点,则______.
三、解答题
19.计算:(1);
(2).
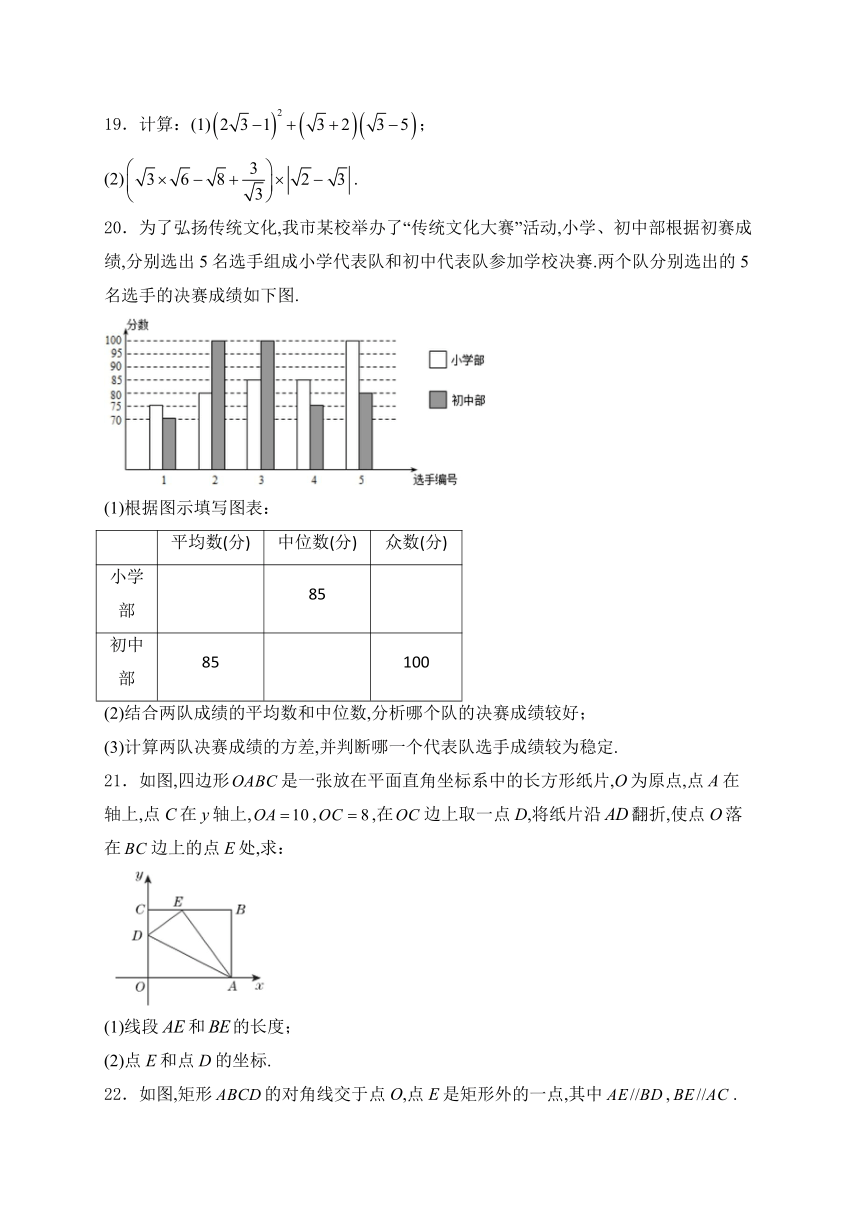
20.为了弘扬传统文化,我市某校举办了“传统文化大赛”活动,小学、初中部根据初赛成绩,分别选出5名选手组成小学代表队和初中代表队参加学校决赛.两个队分别选出的5名选手的决赛成绩如下图.
(1)根据图示填写图表:
平均数(分) 中位数(分) 众数(分)
小学部 85
初中部 85 100
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.
21.如图,四边形是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在轴上,点C在y轴上,,,在边上取一点D,将纸片沿翻折,使点O落在边上的点E处,求:
(1)线段和的长度;
(2)点E和点D的坐标.
22.如图,矩形的对角线交于点O,点E是矩形外的一点,其中,.
(1)求证:四边形是菱形;
(2)求证;
(3)若,连接交于于点F,连接,求证:平分.
23.“琅琅书声浸校园,悠悠书韵满人生”,为提升学生的文学素养,培养学生的阅读兴趣,某校启动校园“读书季”,并计划购进A,B两种图书作为年级竞诵活动的奖品,经调查,购进A种图书的总费用y元与购进A种图书本数之间的函数关系如图所示:
(1)当和时,求y与之间的函数关系式;
(2)现学校准备购进A,B两种图书共300本,已知B种图书每本22元.若购进A种图书不少于60本,且不超过B种图书本数的2倍,购进两种图书的总费用为w元.请求出符合条件的w与之间的函数表达式,并说明怎样购买A,B两种图书才能使总费用最少?总费用最少为多少元?
24.在平面直角坐标系中,一次函数的图象交x轴、y轴分别于A、B两点,交直线于点P.
(1)求点A、B的坐标;
(2)若,求k的值;
(3)在(2)的条件下,C是线段上一点,过点C作轴的垂线,与轴交于点E,与直线交于点D,若,求C点的坐标.
(4)在(2)的条件下,M是y轴上一点,当时,求M点的坐标.
25.我们规定:一组邻边相等且对角互补的四边形叫做完美四边形.
(1)在以下四种四边形中,一定是完美四边形的是______(请填序号):
①平行四边形 ②菱形 ③矩形 ④正方形
(2)如图1,菱形中,E,F分别是,上的点,且,求证:四边形是完美四边形;
(3)完美四边形中,,,连接.
①如图2,求证平分;
②如图3,当时,直接用等式表示出线段,,之间的数量关系.
参考答案
1.答案:B
解析:A、,
不是最简二次根式,故本选项不符合题意;
B、是最简二次根式,故本选项符合题意;
C、,
不是最简二次根式,故本选项不符合题意;
D、,
不是最简二次根式,故本选项不符合题意;
故选:B.
2.答案:D
解析:A、,,,
为直角三角形,故此选项不合题意;
B、设,,,
,
解得:,
则,
所以为直角三角形,故此选项不合题意;
C、,,
为直角三角形,故此选项不合题意;
D、,设,,,
,
不是直角三角形,故此选项符合题意;
故选:D.
3.答案:C
解析:由条形统计图中出现频数最大条形最高的数据是在第三组,7环,故众数是7(环);
因图中是按从小到大的顺序排列的,最中间的环数是7(环)、8(环),故中位数是7.5(环).
故选C.
4.答案:B
解析:依题意,设“数学风车”中的四个直角三角形的斜边长为x,
则
所以
所以“数学风车”的周长是:
.
故选:B.
5.答案:D
解析:
6.答案:A
解析:点、点在一次函数的图象上,
当时,由题意可知,
随x的增大而减小,
,解得.
故选:A.
7.答案:C
解析:
8.答案:A
解析:不等式可变形为:,
即寻找直线在x轴上方的图象,
直线的图象与x轴交于点,
故不等式的解集为:
故选:A
9.答案:C
解析:是菱形ABCD对角线的交点,
;
,
,
,
;
,
,
是直角三角形,
是斜边的中线,
.
故选:C.
10.答案:D
解析:由图象可知:①月上网时间不足35小时,选择方式A最省钱,说法正确;
②月上网时间超过35小时且不足80小时,选择方式B最省钱,说法正确;
③对于上网方式B,若月上网时间在60小时以内,则月收费金额为60元,说法正确;
④对于上网方式C,无论月上网时间是多久月收费都是120元,说法正确;
所以所有合理推断的序号是①②③④.
故选:D.
11.答案:D
解析:作点A关于y轴的对称点,连接,
此时的周长最小值为的长;
A的坐标为
D是OB的中点,
,
由对称可知,
设的直线解析式为,则:
,
解得:,
,
当时,
故选:D.
12.答案:B
解析:
13.答案:且
解析:由題意,得:,解得:且;
故答案为:且.
14.答案:89
解析:
15.答案:2.4
解析:四边形ABCD是菱形,
,
,
,
在中,
如图所示,连接OP,
于点E,于点F
四边形OEPF是矩形,则,
当时,OP的值最小,即EF的值最小,
,
的最小值为2.4,
故答案为:2.4.
16.答案:
解析:把代入可得则点
则两个函数的交点坐标是,
则关于x,y的方程组的解是
故答案为:.
17.答案:360
解析:设甲的速度为米/分钟,乙的速度为米/分钟,
米/分钟
由图象可知:乙追上甲需要12分钟,
米/分钟,
此时乙共走了米,
乙离终点还有米,
乙到达终点时需要的时间为:分钟,
甲离终点还有米,故答案为:360.
18.答案:13
解析:连接BD,取BD的中点F,连接M、N、F,如图所示
、N、F分别是AB、DE、BD的中点
、分别是、的中位线
,,,,
,
,
,
,
,
在中,由勾股定理得
故答案为:13.
19.答案:(1)
(2)1
解析:(1)
(2)原式.
20.答案:(1)85,85,80
(2)小学部决赛成绩较好
(3)小学代表队选手成绩较为稳定
解析:(1)填表:小学部平均数为85分,众数为85分;初中部中位数为80分.
故答案:85,85,80.
(2)小学部成绩较好.两个队的平均数都相同,小学部的中位数高,
在平均数相同的情况下,中位数高的小学部决赛成绩较好.
(3),
,
小学中学
小学代表队选手成绩较为稳定.
21.答案:(1)6
(2)
解析:(1)依题意可知,折痕是四边形的对称轴,
在中,,
,.
(2),,,
.
又,设,则,
在中,.
,,即,.
综上,D点坐标为,E点坐标为
22.答案:证明见解析
解析:证明:(1),,
四边形是平行四边形,
四边形是矩形,
,,
四边形是菱形;
(2)四边形是菱形,
,,,
四边形是矩形,
,,
在和中,,
;
(3),,
,,,
,是等边三角形,
,平分.
23.答案:(1)
(2)最少为6450元
解析:(1)①当时,设函数解析式为
把代入得:
②当时,设函数解析式为
把,分别代入得:
;解得:
.
(2)设购进A种图书本,则购进B种图书本.
由题意可得:,解得:
∴购进两种图书的总费用:
,w随的增大而减小.
,当时,w最小.
当购进A种图书200本,B种图书100本时,总费用最少为6450元.
24.答案:(1)
(2)
(3)
(4),或
解析:(1)令,则
点坐标为,
令,则
点坐标为;
(2)过点P做轴的垂线,交轴于点M,
点坐标为,
中,,,
把代入中,得
点坐标为
把代入中,可得:,解得:;
(3)是直线上一点;设C点坐标为
则点D坐标为,点E坐标为
,
,,
解得,点坐标为;
(4)点坐标为,点坐标为
,,
,
,
,或.
25.答案:(1)④
(2)证明见解析
(3)①证明见解析
②
解析:(1)④
(2)证明:连接,四边形是菱形,
,,
和都是等边三角形,
,,
在和中,
,,.
,.
四边形是完美四边形.
(3)①延长到点E,使,连接,
,,
.
又,
,,
,.
即平分(做法不唯一)
②.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列二次根式中,是最简二次根式的是( )
A. B. C. D.
2.中,,的对边分别记为a,b,c,下列条件不能判定为直角三角形的是( )
A. B.
C. D.
3.某射击小组有20人,教练根据他们某次射击的数据绘制成如图所示的统计图,则这组数据的众数和中位数分别是( )
A.7,7 B.8,7.5 C.7,7.5 D.8,6.5
4.下列有关一次函数的说法中,错误的是( )
A.y的值随着值的增大而减小 B.函数图象与轴的交点坐标为
C.当时 D.函数图象经过第一、二、四象限
5.如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若,,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是( )
A.72 B.52 C.80 D.76
6.已知点,点在一次函数的图像上,且,则m的取值范围是( )
A. B. C. D.
7.如图,要使平行四边形成为矩形,需添加的条件是( )
A. B. C. D.
8.如图,直线交坐标轴于,两点,则不等式的解集为( )
A. B. C. D.
9.如图,菱形的对角线,相交于点O.过点C作于点E.连接.若,,则的长为( )
A.2 B. C.6 D.8
10.A,B,C三种上宽带网方式的月收费金额(元),(元)(元)与月上网时间(小时)的对应关系如图所示,以下有四个推断:
①月上网时间不足35小时,选择方式A最省钱;
②月上网时间超过35小时且不足80小时,选择方式B最省线;
③对于上网方式B,若月上网时间在60小时以内,则月收费金额为60元;
④对于上网方式C,无论月上网时间是多久,月收费都是120元;
所有合理推断的序号是( )
A.①②③ B.①②③ C.②③④ D.①②③④
11.如图,在平面直角坐标系中,点A的坐标为,轴,轴,D是的中点,E是上的一点,当的周长最小时,点E的坐标是( )
A. B. C. D.
12.如图,在平行四边形中,对角线,相交于O,,E,F,G分别是,,的中点,下列结论:
①;②;③;④平分;⑤四边形是菱形.其中正确的是( )
A.①②③ B.①③④ C.①②⑤ D.②③⑤
二、填空题
13.若代数式有意义,则x的取值范围为______.
14.某校规定学生的数学学期综合成绩是由平时、期中和期末三项成绩按的比计算所得.若某同学本学期数学的平时、期中和期末成绩分别是80分、90分和95分,则他本学期数学学期综合成绩是______分.
15.如图,菱形的对角线,相交于点O,点P为边上一动点(不与点A,B重合),于点E,于点F.若,,则的最小值为______.
16.如图已知函数和的图象交于点P,点P的横坐标为1,则关于,y和x的方程组的解是______.
17.甲、乙两人在笔直的湖边公路上,同起点,同终点、同方向匀速步行2400米,先到终点的人原地休息,已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发时间(分钟)之间的关系如图所示,则乙到达终点时,甲离终点还有______米.
18.如图,已知在中,,点D是延长线上的一点,,点E是上一点,,连接,M,N分别是、的中点,则______.
三、解答题
19.计算:(1);
(2).
20.为了弘扬传统文化,我市某校举办了“传统文化大赛”活动,小学、初中部根据初赛成绩,分别选出5名选手组成小学代表队和初中代表队参加学校决赛.两个队分别选出的5名选手的决赛成绩如下图.
(1)根据图示填写图表:
平均数(分) 中位数(分) 众数(分)
小学部 85
初中部 85 100
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.
21.如图,四边形是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在轴上,点C在y轴上,,,在边上取一点D,将纸片沿翻折,使点O落在边上的点E处,求:
(1)线段和的长度;
(2)点E和点D的坐标.
22.如图,矩形的对角线交于点O,点E是矩形外的一点,其中,.
(1)求证:四边形是菱形;
(2)求证;
(3)若,连接交于于点F,连接,求证:平分.
23.“琅琅书声浸校园,悠悠书韵满人生”,为提升学生的文学素养,培养学生的阅读兴趣,某校启动校园“读书季”,并计划购进A,B两种图书作为年级竞诵活动的奖品,经调查,购进A种图书的总费用y元与购进A种图书本数之间的函数关系如图所示:
(1)当和时,求y与之间的函数关系式;
(2)现学校准备购进A,B两种图书共300本,已知B种图书每本22元.若购进A种图书不少于60本,且不超过B种图书本数的2倍,购进两种图书的总费用为w元.请求出符合条件的w与之间的函数表达式,并说明怎样购买A,B两种图书才能使总费用最少?总费用最少为多少元?
24.在平面直角坐标系中,一次函数的图象交x轴、y轴分别于A、B两点,交直线于点P.
(1)求点A、B的坐标;
(2)若,求k的值;
(3)在(2)的条件下,C是线段上一点,过点C作轴的垂线,与轴交于点E,与直线交于点D,若,求C点的坐标.
(4)在(2)的条件下,M是y轴上一点,当时,求M点的坐标.
25.我们规定:一组邻边相等且对角互补的四边形叫做完美四边形.
(1)在以下四种四边形中,一定是完美四边形的是______(请填序号):
①平行四边形 ②菱形 ③矩形 ④正方形
(2)如图1,菱形中,E,F分别是,上的点,且,求证:四边形是完美四边形;
(3)完美四边形中,,,连接.
①如图2,求证平分;
②如图3,当时,直接用等式表示出线段,,之间的数量关系.
参考答案
1.答案:B
解析:A、,
不是最简二次根式,故本选项不符合题意;
B、是最简二次根式,故本选项符合题意;
C、,
不是最简二次根式,故本选项不符合题意;
D、,
不是最简二次根式,故本选项不符合题意;
故选:B.
2.答案:D
解析:A、,,,
为直角三角形,故此选项不合题意;
B、设,,,
,
解得:,
则,
所以为直角三角形,故此选项不合题意;
C、,,
为直角三角形,故此选项不合题意;
D、,设,,,
,
不是直角三角形,故此选项符合题意;
故选:D.
3.答案:C
解析:由条形统计图中出现频数最大条形最高的数据是在第三组,7环,故众数是7(环);
因图中是按从小到大的顺序排列的,最中间的环数是7(环)、8(环),故中位数是7.5(环).
故选C.
4.答案:B
解析:依题意,设“数学风车”中的四个直角三角形的斜边长为x,
则
所以
所以“数学风车”的周长是:
.
故选:B.
5.答案:D
解析:
6.答案:A
解析:点、点在一次函数的图象上,
当时,由题意可知,
随x的增大而减小,
,解得.
故选:A.
7.答案:C
解析:
8.答案:A
解析:不等式可变形为:,
即寻找直线在x轴上方的图象,
直线的图象与x轴交于点,
故不等式的解集为:
故选:A
9.答案:C
解析:是菱形ABCD对角线的交点,
;
,
,
,
;
,
,
是直角三角形,
是斜边的中线,
.
故选:C.
10.答案:D
解析:由图象可知:①月上网时间不足35小时,选择方式A最省钱,说法正确;
②月上网时间超过35小时且不足80小时,选择方式B最省钱,说法正确;
③对于上网方式B,若月上网时间在60小时以内,则月收费金额为60元,说法正确;
④对于上网方式C,无论月上网时间是多久月收费都是120元,说法正确;
所以所有合理推断的序号是①②③④.
故选:D.
11.答案:D
解析:作点A关于y轴的对称点,连接,
此时的周长最小值为的长;
A的坐标为
D是OB的中点,
,
由对称可知,
设的直线解析式为,则:
,
解得:,
,
当时,
故选:D.
12.答案:B
解析:
13.答案:且
解析:由題意,得:,解得:且;
故答案为:且.
14.答案:89
解析:
15.答案:2.4
解析:四边形ABCD是菱形,
,
,
,
在中,
如图所示,连接OP,
于点E,于点F
四边形OEPF是矩形,则,
当时,OP的值最小,即EF的值最小,
,
的最小值为2.4,
故答案为:2.4.
16.答案:
解析:把代入可得则点
则两个函数的交点坐标是,
则关于x,y的方程组的解是
故答案为:.
17.答案:360
解析:设甲的速度为米/分钟,乙的速度为米/分钟,
米/分钟
由图象可知:乙追上甲需要12分钟,
米/分钟,
此时乙共走了米,
乙离终点还有米,
乙到达终点时需要的时间为:分钟,
甲离终点还有米,故答案为:360.
18.答案:13
解析:连接BD,取BD的中点F,连接M、N、F,如图所示
、N、F分别是AB、DE、BD的中点
、分别是、的中位线
,,,,
,
,
,
,
,
在中,由勾股定理得
故答案为:13.
19.答案:(1)
(2)1
解析:(1)
(2)原式.
20.答案:(1)85,85,80
(2)小学部决赛成绩较好
(3)小学代表队选手成绩较为稳定
解析:(1)填表:小学部平均数为85分,众数为85分;初中部中位数为80分.
故答案:85,85,80.
(2)小学部成绩较好.两个队的平均数都相同,小学部的中位数高,
在平均数相同的情况下,中位数高的小学部决赛成绩较好.
(3),
,
小学中学
小学代表队选手成绩较为稳定.
21.答案:(1)6
(2)
解析:(1)依题意可知,折痕是四边形的对称轴,
在中,,
,.
(2),,,
.
又,设,则,
在中,.
,,即,.
综上,D点坐标为,E点坐标为
22.答案:证明见解析
解析:证明:(1),,
四边形是平行四边形,
四边形是矩形,
,,
四边形是菱形;
(2)四边形是菱形,
,,,
四边形是矩形,
,,
在和中,,
;
(3),,
,,,
,是等边三角形,
,平分.
23.答案:(1)
(2)最少为6450元
解析:(1)①当时,设函数解析式为
把代入得:
②当时,设函数解析式为
把,分别代入得:
;解得:
.
(2)设购进A种图书本,则购进B种图书本.
由题意可得:,解得:
∴购进两种图书的总费用:
,w随的增大而减小.
,当时,w最小.
当购进A种图书200本,B种图书100本时,总费用最少为6450元.
24.答案:(1)
(2)
(3)
(4),或
解析:(1)令,则
点坐标为,
令,则
点坐标为;
(2)过点P做轴的垂线,交轴于点M,
点坐标为,
中,,,
把代入中,得
点坐标为
把代入中,可得:,解得:;
(3)是直线上一点;设C点坐标为
则点D坐标为,点E坐标为
,
,,
解得,点坐标为;
(4)点坐标为,点坐标为
,,
,
,
,或.
25.答案:(1)④
(2)证明见解析
(3)①证明见解析
②
解析:(1)④
(2)证明:连接,四边形是菱形,
,,
和都是等边三角形,
,,
在和中,
,,.
,.
四边形是完美四边形.
(3)①延长到点E,使,连接,
,,
.
又,
,,
,.
即平分(做法不唯一)
②.
同课章节目录
