3.3 中心对称 课件(共22张PPT)
文档属性
| 名称 | 3.3 中心对称 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 910.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-30 08:02:30 | ||
图片预览







文档简介
(共22张PPT)
3.3 中心对称
第三章 图形的平移与旋转
1.通过观察实例、猜想、动画验证、尝试归纳等活动,知道两个图形成中心对称的概念.
2.通过感知、举例、说理等活动,能总结出成中心对称的性质及性质的简单应用.
3.通过观察、思考、动手操作、尝试归纳等活动,知道中心对称图形的概念,并能通过
对线段等实例的分析总结出线段、正多边形的中心对称性质.
4.通过对太极图等生活实例的观察,认识并欣赏自然界和现实生活中的中心对称图形.
学习目标
温故知新
什么样的图形运动称为旋转呢
在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称为旋转,这个定点称为旋转中心,转动的角称为旋转角.旋转不改变图形的形状和大小.
旋转的基本性质
2.A0= ,BO= ,CO= ,
依据是:
3.∠AOD= = =40°,
依据是:
1.△ABC≌ .
依据是:
△DEF
旋转不改变图形的形状和大小.
对应点到旋转中心的距离相等.
D0
EO
FO
∠BOE
∠COF
任意一组对应点与旋转中心的连线所成的角都等于旋转角.
新课学习
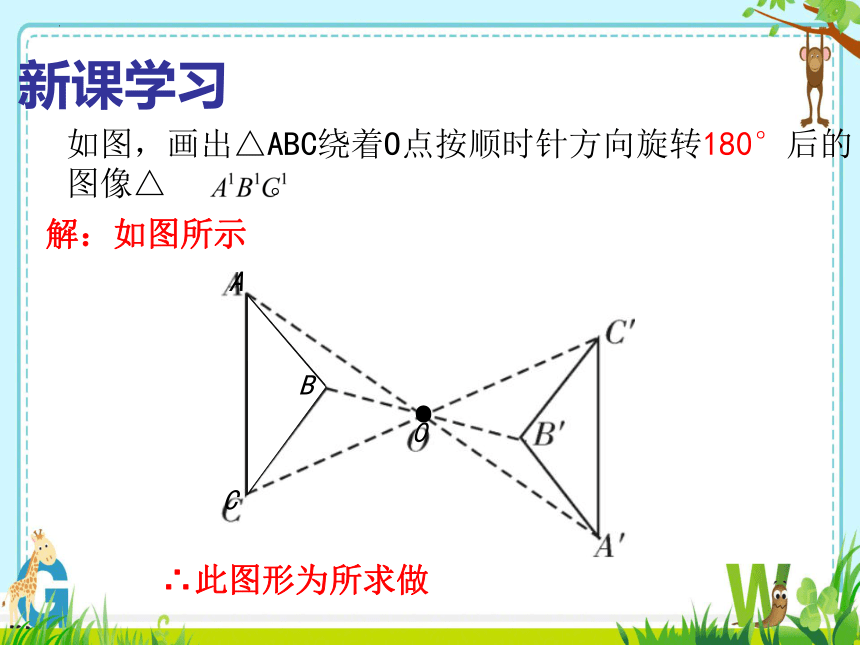
如图,画出△ABC绕着O点按顺时针方向旋转180°后的图像△ 。
解:如图所示
∴此图形为所求做
A
B
C
0
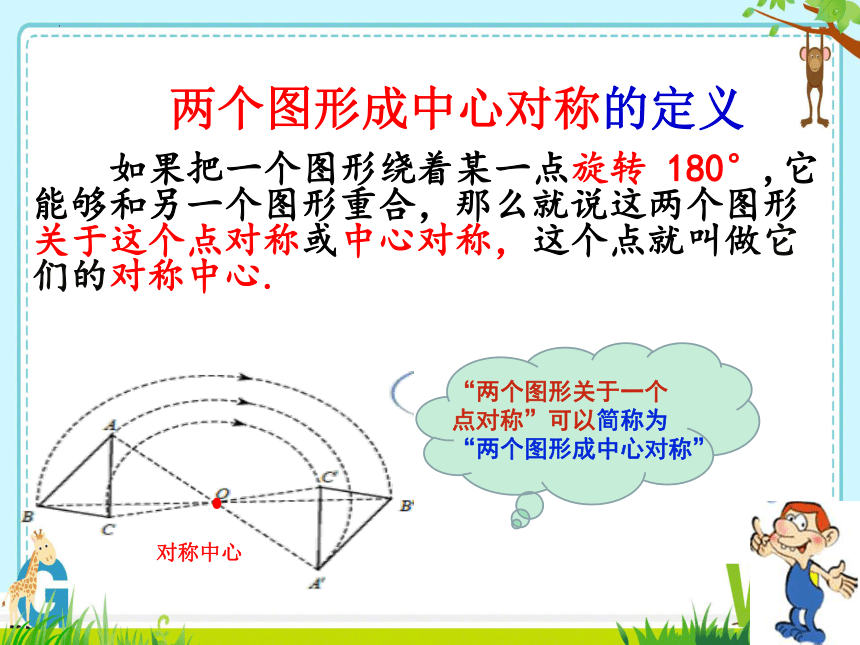
如果把一个图形绕着某一点旋转 180°,它能够和另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点就叫做它们的对称中心.
“两个图形关于一个
点对称”可以简称为
“两个图形成中心对称”
两个图形成中心对称的定义
对称中心
如图,△ABC与△A'B'C'关于点O成中心对称,则:
(1)AO= ,BO= ,CO= ;
(2)点A,O与 三点在同一直线上;
(3)线段AA',BB',CC'的中点都是点 ;
(4)AB∥ ,BC∥ ,AC∥ .
A'O
B'O
C'O
A'
O
A'B'
B'C'
A' C'
两个图形成中心对称的性质
(1)关于中心对称的两个图形是全等图形;
(2)成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分.
如图,点O是线段AE的中点,以点O为对称中心,画出与五边形成中心对称的图形.(对称中心在图像上)
例题讲解
如图,点O是线段AE的中点,以点O为对称中心,画出与五边形成中心对称的图形.(对称中心在图像上)
解:如图所示,连接 BO 并延长至点 B′,
使得 OB′=OB.
连接 CO 并延长至点 C′,使得OC′=OC.
连接 DO 并延长至点D′,使得OD′=OD.
顺次连接点 E, B′,C′,D′,A.
图形 E B′ C′ D′A 就是以点 O 为对称中心,
与五边形 ABCDE 成中心对称的图形.
例题讲解
如下图 中的图形旋转多少度与自身重合?
A
B
O
新课学习
中心对称图形的定义
把一个图形绕某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
注意:平行四边形不是轴对称图形,是中心对称图形
中心对称与中心对称图形的联系与区别
区别:
中心对称指两个全等图形的相互位置关系,中心对称图形指一个图形本身成中心对称.
联系:
如果将成中心对称的两个图形看成一个整体,则它们是中心对称图形.
如果将中心对称图形对称的部分看成两个图形,则它们成中心对称.
在上面的例题中,图形 ABCDEB′C′D′ 是中心对称 图形吗?
议一议
边数为偶数的正多边形都是中心对称图形.
正三角形
正四边形
正六边形
正五边形
线段
等腰梯形
是
火眼金睛:判断下列图形是否是中心对称图形,如果是,请指出其对称中心.
正七边形
正八边形
不是
不是
是
不是
是
不是
是
课堂练习
1.下列图形中,既是轴对称图形又是中心对称图形的
是 ( )
D
2.如图是一个以点0为对称中心的中心对称图形,若∠A=30°,∠C=90°,OC=1,则AB的长为( )
B
A.2 B.4 C. D.
3.下列哪些扑克牌中,哪些牌的牌面是中心对称图形?
√
√
4.在艺术字中,有些汉字或字母是中心对称图形.下面的汉字或字母,是中心对称图形吗?如果是,请标出它们的对称中心。
5.如图,直线l与直线m交于点P,作出△ABC关于点P成中心对称的图形。
解:如图所示
∴△A1B1C1为所求作.
6.如图 △ABO与△CDO关于点0成中心对称,点E,F在线段AC 上,且AF=CE.求证:FD=BE。
7.如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE。
(1)图中哪两个图形成中心对称 (2)若△ADC的面积为4,求△ABE的面积。(3)若AB=5.AC=3,求线段AD的取值范围。
拓展练习
解:(1)△ADC和△EDB成中心对称.
(2)∵由(1)知△ADC和△EDB成中心对称
∴S△EDB=S△ADC=4
∵D为BC的中点,即BD=DC ∴S△ABD=S△ADC=4 ∴S△ABE=S△ABD+S△EDB=4+4=8.
(3)∵由(1)得△ADC和△EDB成中心对称
∴AC=BE=3 AE=2AD
∵在△ABE中,AB-BE<AE<AB+BE
即2<AE<8 ∴1<AD<4
回顾反思
这节课我的收获是……
谢谢同学们!
再见!
3.3 中心对称
第三章 图形的平移与旋转
1.通过观察实例、猜想、动画验证、尝试归纳等活动,知道两个图形成中心对称的概念.
2.通过感知、举例、说理等活动,能总结出成中心对称的性质及性质的简单应用.
3.通过观察、思考、动手操作、尝试归纳等活动,知道中心对称图形的概念,并能通过
对线段等实例的分析总结出线段、正多边形的中心对称性质.
4.通过对太极图等生活实例的观察,认识并欣赏自然界和现实生活中的中心对称图形.
学习目标
温故知新
什么样的图形运动称为旋转呢
在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称为旋转,这个定点称为旋转中心,转动的角称为旋转角.旋转不改变图形的形状和大小.
旋转的基本性质
2.A0= ,BO= ,CO= ,
依据是:
3.∠AOD= = =40°,
依据是:
1.△ABC≌ .
依据是:
△DEF
旋转不改变图形的形状和大小.
对应点到旋转中心的距离相等.
D0
EO
FO
∠BOE
∠COF
任意一组对应点与旋转中心的连线所成的角都等于旋转角.
新课学习
如图,画出△ABC绕着O点按顺时针方向旋转180°后的图像△ 。
解:如图所示
∴此图形为所求做
A
B
C
0
如果把一个图形绕着某一点旋转 180°,它能够和另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点就叫做它们的对称中心.
“两个图形关于一个
点对称”可以简称为
“两个图形成中心对称”
两个图形成中心对称的定义
对称中心
如图,△ABC与△A'B'C'关于点O成中心对称,则:
(1)AO= ,BO= ,CO= ;
(2)点A,O与 三点在同一直线上;
(3)线段AA',BB',CC'的中点都是点 ;
(4)AB∥ ,BC∥ ,AC∥ .
A'O
B'O
C'O
A'
O
A'B'
B'C'
A' C'
两个图形成中心对称的性质
(1)关于中心对称的两个图形是全等图形;
(2)成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分.
如图,点O是线段AE的中点,以点O为对称中心,画出与五边形成中心对称的图形.(对称中心在图像上)
例题讲解
如图,点O是线段AE的中点,以点O为对称中心,画出与五边形成中心对称的图形.(对称中心在图像上)
解:如图所示,连接 BO 并延长至点 B′,
使得 OB′=OB.
连接 CO 并延长至点 C′,使得OC′=OC.
连接 DO 并延长至点D′,使得OD′=OD.
顺次连接点 E, B′,C′,D′,A.
图形 E B′ C′ D′A 就是以点 O 为对称中心,
与五边形 ABCDE 成中心对称的图形.
例题讲解
如下图 中的图形旋转多少度与自身重合?
A
B
O
新课学习
中心对称图形的定义
把一个图形绕某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
注意:平行四边形不是轴对称图形,是中心对称图形
中心对称与中心对称图形的联系与区别
区别:
中心对称指两个全等图形的相互位置关系,中心对称图形指一个图形本身成中心对称.
联系:
如果将成中心对称的两个图形看成一个整体,则它们是中心对称图形.
如果将中心对称图形对称的部分看成两个图形,则它们成中心对称.
在上面的例题中,图形 ABCDEB′C′D′ 是中心对称 图形吗?
议一议
边数为偶数的正多边形都是中心对称图形.
正三角形
正四边形
正六边形
正五边形
线段
等腰梯形
是
火眼金睛:判断下列图形是否是中心对称图形,如果是,请指出其对称中心.
正七边形
正八边形
不是
不是
是
不是
是
不是
是
课堂练习
1.下列图形中,既是轴对称图形又是中心对称图形的
是 ( )
D
2.如图是一个以点0为对称中心的中心对称图形,若∠A=30°,∠C=90°,OC=1,则AB的长为( )
B
A.2 B.4 C. D.
3.下列哪些扑克牌中,哪些牌的牌面是中心对称图形?
√
√
4.在艺术字中,有些汉字或字母是中心对称图形.下面的汉字或字母,是中心对称图形吗?如果是,请标出它们的对称中心。
5.如图,直线l与直线m交于点P,作出△ABC关于点P成中心对称的图形。
解:如图所示
∴△A1B1C1为所求作.
6.如图 △ABO与△CDO关于点0成中心对称,点E,F在线段AC 上,且AF=CE.求证:FD=BE。
7.如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE。
(1)图中哪两个图形成中心对称 (2)若△ADC的面积为4,求△ABE的面积。(3)若AB=5.AC=3,求线段AD的取值范围。
拓展练习
解:(1)△ADC和△EDB成中心对称.
(2)∵由(1)知△ADC和△EDB成中心对称
∴S△EDB=S△ADC=4
∵D为BC的中点,即BD=DC ∴S△ABD=S△ADC=4 ∴S△ABE=S△ABD+S△EDB=4+4=8.
(3)∵由(1)得△ADC和△EDB成中心对称
∴AC=BE=3 AE=2AD
∵在△ABE中,AB-BE<AE<AB+BE
即2<AE<8 ∴1<AD<4
回顾反思
这节课我的收获是……
谢谢同学们!
再见!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
