2.5.1 有理数的乘法与除法:乘法、乘法运算律 同步课件 (共37张PPT)
文档属性
| 名称 | 2.5.1 有理数的乘法与除法:乘法、乘法运算律 同步课件 (共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 37.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-30 17:50:58 | ||
图片预览











文档简介
(共37张PPT)
第2章 有理数
2.5.1 有理数的乘法与除法:
乘法、乘法运算律
教学目标
01
贴近生活实例感受有理数的乘法,理解有理数乘法法则
03
02
熟悉有理数乘法运算律
能灵活运用有理数乘法法则和乘法运算律进行运算
有理数的乘法
01
课堂引入
小学里,我们学过非负有理数的乘法和除法运算,引入负数后,怎样进行乘法和除法运算呢?
01
课堂引入
问题——在水文观测中,常常关注水位的高低与升降。如果水位每天下降4cm,那么如何计算3天后的水位变化?
今天的水位
3天后
3天后的水位比现在的水位下降12cm。如果规定水位上升记为正,下降记为负,那么我们有:
(-4)×3=12
01
课堂引入
∵4×3=12,
∴(-4)×3是4×3的相反数。
我们也可以用相反数的意义来说明(-4)×3=-12。
∵(-4)×3+4×3=[(-4)+4]×3=0,
∴(-4)×3是4×3的相反数,
∴(-4)×3=-12。
当数扩充到有理数后,乘法分配率仍然适用
探究——如何计算4×(-3),(-4)×(-3)?
01
课堂引入
【分析】
∵4×(-3)是4×3的相反数,
∴4×(-3)=-12;
∵(-4)×(-3)是(-4)×3的相反数,
∴(-4)×(-3)=12。
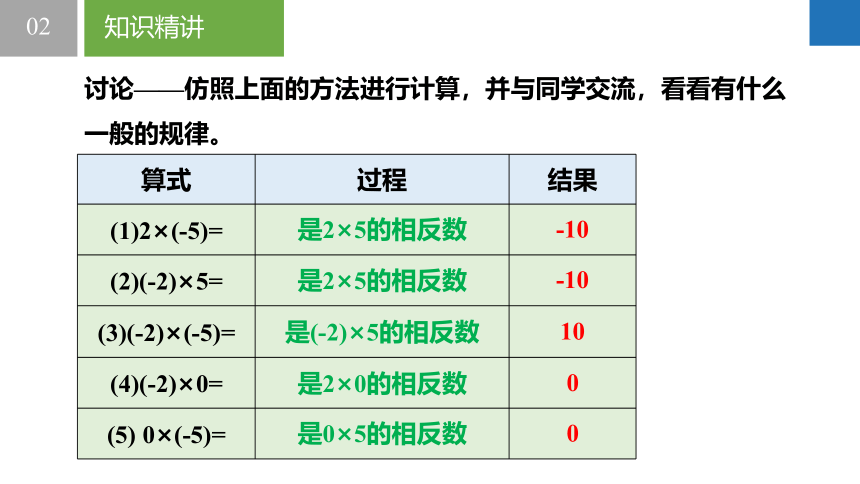
讨论——仿照上面的方法进行计算,并与同学交流,看看有什么一般的规律。
算式 过程 结果
(1)2×(-5)=
(2)(-2)×5=
(3)(-2)×(-5)=
(4)(-2)×0=
(5) 0×(-5)=
是0×5的相反数 0
是2×5的相反数 -10
是2×5的相反数 -10
是(-2)×5的相反数 10
是2×0的相反数 0
02
知识精讲
02
知识精讲
有理数乘法法则
1.两数相乘,同号得正,异号得负(定号),并把绝对值相乘(定值)。
2.0与任何数相乘都得0。
例1、
算式 定号 定值 结果
(1)52×(-1)=
(2)(-52)×(-1)=
03
典例精析
- 52×1 -52
+ 52×1 52
一个数乘-1等于这个数的相反数
×(-1)
a -a
×(-1)
例2、
算式 定号 定值 结果
(1)2×(-16)=
(2)(-2)×(-16)=
(3)(-)×1=
(4)(-)×(-1)=
(5) (-8.037)×0=
03
典例精析
- 2×16 -32
+ 2×16 32
- × -
加减运算中,带分数的两种处理方式:
①化成假分数,②拆项;
但在乘除运算中,带分数一定要化成假分数。
(3)原式=(-)×
例2、
算式 定号 定值 结果
(1)2×(-16)=
(2)(-2)×(-16)=
(3)(-)×1=
(4)(-)×(-1)=
(5) (-8.037)×0=
03
典例精析
- 2×16 -32
+ 2×16 32
- × -
+ ×
0
探究——a×(-b)与a×b有什么关系?
【分析】a×(-b)与a×b互为相反数。
03
典例精析
有理数的乘法
——多数相乘
算一算,找规律
(-1)×(-2)=
(-1)×(-2)×(-3)=
(-1)×(-2)×(-3)×(-4)=
(+1)×(-2)×(-3)×(-4)×(-5)=
…
(-1)×(-2)×0×(-3)×(-4)×(-5)×…=
2
-6
+24
-120
【总结】
几个不等于0的数相乘,
当负因数有奇数个时,积为负;
当负因数有偶数个时,积为正。
0
几个数相乘,有一个因数为0,积就为0。
01
课堂引入
02
知识精讲
有理数乘法法则
多数相乘,
①所有因数都不为0,
当负因数有奇数个时,积为负,
当负因数有偶数个时,积为正(定号);
并把绝对值相乘(定值)。
②有一个因数为0,积就为0。
口诀:奇负偶正
例1、判断下列说法是否正确。
(1)两数之积为正,这两数同正
(2)两数之积为负,这两数异号
(3)几个数相乘,积的符号由负因数的个数决定
(4)三数相乘,积为负,这三个数都是负数
×,有可能两数同负
03
典例精析
(4)×,有可能两正一负
(3)×,应改成“几个不等于0的数相乘”
√
例2、
算式 定号 定值 结果
(1)(-3)×0×(-8)×2.5=
(2)(-5)×(-)×(-)=
(3)(-2)×(-8)×1=
(4)(-)×(-2.5)×(-)×(-8)=
(5) (-)×1×(-)×(-5)=
03
典例精析
0
- 5×× -
在乘除运算中,带分数一定要化成假分数
(3)原式=(-2)×(-8)×
+ 2×8× 17
例2、
算式 定号 定值 结果
(1)(-3)×0×(-8)×2.5=
(2)(-5)×(-)×(-)=
(3)(-2)×(-8)×1=
(4)(-)×(-2.5)×(-)×(-8)=
(5) (-)×1×(-)×(-5)=
03
典例精析
0
- 5×× -
(4)原式=(-)×(-)×(-)×(-8)
+ 2×8× 17
在乘除运算中,小数一定要化成分数
+ ×××8
- ×××5 -
有理数乘法运算律
1-1:黑板上两个算式的结果相等吗?
相等
相等,eg:(-5)×3=3×(-5)=-15,(-2)×(-7)=(-7)×(-2)=14,……
6
× = _____
-7
× = _____
6
-7
-42
-42
1-2:把△、○中的数换成其他有理数,结果仍然相等吗?
01
课堂引入
1-1:黑板上两个算式的结果相等吗?
相等
相等,eg:[(-5)×3]×4=(-5)×(3×4)=-60,
[(-2)×(-7)]×3=(-2)×[(-7)×3]=42,……
1-2:把△、○、□中的数换成其他有理数,结果仍然相等吗?
( × ) × = _____
3
-5
3
× ( × ) = _____
-5
-2
-2
30
30
01
课堂引入
( + ) × = _____
-3
5
-3
× + × = _____
5
4
4
4
1-1:黑板上两个算式的结果相等吗?
相等
相等,eg:[(-5)+3]×2=(-5)×2+3×2=-4,
[(-2)+(-7)]×7=(-2)×7+(-7)×7=-63,……
1-2:把△、○、□中的数换成其他有理数,结果仍然相等吗?
8
8
01
课堂引入
事实上,小学里学过的乘法交换律、乘法结合律、乘法分配律,在有理数范围内仍然适用。
加法运算律
02
知识精讲
有理数乘法运算律
有理数乘法运算律:
①交换律:a×b=b×a,
②结合律:(a×b)×c=a×(b×c),
③分配律:(a+b)×c=a×c+b×c。
计算:(1)(-16)×(+2)×(-) (2)(-)×24
交换律
02
知识精讲
=+(16×2×)
=+(16××2)
=2
分配律
=×24-×24
=10-21
=-11
(3)-12×(-+)
分配律
02
知识精讲
=(-12)×+(-12)×(-)+(-12)×
=-3+8+(-2)
=3
(4)9×(-5)+(-111)×(-5)-(-2)×(-5)
=(-5)×[9+(-111)-(-2)]
=(-5)×[9+(-111)-(-2)]
=(-5)×(-100)
=500
逆用关键:取相同,合不同
02
知识精讲
分配律的逆用:
a×c+b×c=(a+b)×c。
02
知识精讲
计算:(1)16×
(2)(-10)×(-)
(3)(-)×(-)
=1
=+(10×)=1
=+(×)=1
加法运算律
02
知识精讲
倒数
一般地,如果a×b=1,那么a和b互为倒数关系,其中一个数叫作另一个数的倒数。
特别地,0没有倒数。
eg:16与,(-10)与(-),(-)与(-)…都互为倒数。
02
知识精讲
试一试:
(1)2的倒数是_______,的倒数是_______;
(2)-2的倒数是_______,-的倒数是_______;
(3)一个数的倒数是它本身的数是_______;
(4)正数的倒数是______,负数的倒数是_______。
2
±1
正数
负数
-
-
倒数
求一个数的倒数的方法 求一个整数的倒数,就是写整数分之一
求一个分数的倒数,就是调换分子和分母的位置
02
知识精讲
例1、(-8)×(-0.25)×(+125)×4
交换律、结合律同时使用
03
典例精析
解:原式
=+(8××125×4)
=+(8×125)×(×4)
=1000
例2、-6×(--+-2)
03
典例精析
解:原式
=(-6)×(-)+(-6)×(-)+(-6)×()+(-6)×(-2)
=9+4+(-5)+12
=20
例3、×(-5)+×(-3.5)+×2
03
典例精析
解:原式
=×[(-5)+(-3.5)+2]
=×(-9+2)
=-
课后总结
有理数乘法法则:
1.两数相乘,同号得正,异号得负(定号),并把绝对值相乘(定值)。
2.0与任何数相乘都得0。
3.多数相乘,
①所有因数都不为0,
当负因数有奇数个时,积为负,
当负因数有偶数个时,积为正(定号);
并把绝对值相乘(定值)。
②有一个因数为0,积就为0。
有理数乘法运算律:
①交换律:a×b=b×a,
②结合律:(a×b)×c=a×(b×c),
③分配律:(a+b)×c=a×c+b×c。
一般地,如果a×b=1,那么a和b互为倒数关系,其中一个数叫作另一个数的倒数。
特别地,0没有倒数。
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第2章 有理数
2.5.1 有理数的乘法与除法:
乘法、乘法运算律
教学目标
01
贴近生活实例感受有理数的乘法,理解有理数乘法法则
03
02
熟悉有理数乘法运算律
能灵活运用有理数乘法法则和乘法运算律进行运算
有理数的乘法
01
课堂引入
小学里,我们学过非负有理数的乘法和除法运算,引入负数后,怎样进行乘法和除法运算呢?
01
课堂引入
问题——在水文观测中,常常关注水位的高低与升降。如果水位每天下降4cm,那么如何计算3天后的水位变化?
今天的水位
3天后
3天后的水位比现在的水位下降12cm。如果规定水位上升记为正,下降记为负,那么我们有:
(-4)×3=12
01
课堂引入
∵4×3=12,
∴(-4)×3是4×3的相反数。
我们也可以用相反数的意义来说明(-4)×3=-12。
∵(-4)×3+4×3=[(-4)+4]×3=0,
∴(-4)×3是4×3的相反数,
∴(-4)×3=-12。
当数扩充到有理数后,乘法分配率仍然适用
探究——如何计算4×(-3),(-4)×(-3)?
01
课堂引入
【分析】
∵4×(-3)是4×3的相反数,
∴4×(-3)=-12;
∵(-4)×(-3)是(-4)×3的相反数,
∴(-4)×(-3)=12。
讨论——仿照上面的方法进行计算,并与同学交流,看看有什么一般的规律。
算式 过程 结果
(1)2×(-5)=
(2)(-2)×5=
(3)(-2)×(-5)=
(4)(-2)×0=
(5) 0×(-5)=
是0×5的相反数 0
是2×5的相反数 -10
是2×5的相反数 -10
是(-2)×5的相反数 10
是2×0的相反数 0
02
知识精讲
02
知识精讲
有理数乘法法则
1.两数相乘,同号得正,异号得负(定号),并把绝对值相乘(定值)。
2.0与任何数相乘都得0。
例1、
算式 定号 定值 结果
(1)52×(-1)=
(2)(-52)×(-1)=
03
典例精析
- 52×1 -52
+ 52×1 52
一个数乘-1等于这个数的相反数
×(-1)
a -a
×(-1)
例2、
算式 定号 定值 结果
(1)2×(-16)=
(2)(-2)×(-16)=
(3)(-)×1=
(4)(-)×(-1)=
(5) (-8.037)×0=
03
典例精析
- 2×16 -32
+ 2×16 32
- × -
加减运算中,带分数的两种处理方式:
①化成假分数,②拆项;
但在乘除运算中,带分数一定要化成假分数。
(3)原式=(-)×
例2、
算式 定号 定值 结果
(1)2×(-16)=
(2)(-2)×(-16)=
(3)(-)×1=
(4)(-)×(-1)=
(5) (-8.037)×0=
03
典例精析
- 2×16 -32
+ 2×16 32
- × -
+ ×
0
探究——a×(-b)与a×b有什么关系?
【分析】a×(-b)与a×b互为相反数。
03
典例精析
有理数的乘法
——多数相乘
算一算,找规律
(-1)×(-2)=
(-1)×(-2)×(-3)=
(-1)×(-2)×(-3)×(-4)=
(+1)×(-2)×(-3)×(-4)×(-5)=
…
(-1)×(-2)×0×(-3)×(-4)×(-5)×…=
2
-6
+24
-120
【总结】
几个不等于0的数相乘,
当负因数有奇数个时,积为负;
当负因数有偶数个时,积为正。
0
几个数相乘,有一个因数为0,积就为0。
01
课堂引入
02
知识精讲
有理数乘法法则
多数相乘,
①所有因数都不为0,
当负因数有奇数个时,积为负,
当负因数有偶数个时,积为正(定号);
并把绝对值相乘(定值)。
②有一个因数为0,积就为0。
口诀:奇负偶正
例1、判断下列说法是否正确。
(1)两数之积为正,这两数同正
(2)两数之积为负,这两数异号
(3)几个数相乘,积的符号由负因数的个数决定
(4)三数相乘,积为负,这三个数都是负数
×,有可能两数同负
03
典例精析
(4)×,有可能两正一负
(3)×,应改成“几个不等于0的数相乘”
√
例2、
算式 定号 定值 结果
(1)(-3)×0×(-8)×2.5=
(2)(-5)×(-)×(-)=
(3)(-2)×(-8)×1=
(4)(-)×(-2.5)×(-)×(-8)=
(5) (-)×1×(-)×(-5)=
03
典例精析
0
- 5×× -
在乘除运算中,带分数一定要化成假分数
(3)原式=(-2)×(-8)×
+ 2×8× 17
例2、
算式 定号 定值 结果
(1)(-3)×0×(-8)×2.5=
(2)(-5)×(-)×(-)=
(3)(-2)×(-8)×1=
(4)(-)×(-2.5)×(-)×(-8)=
(5) (-)×1×(-)×(-5)=
03
典例精析
0
- 5×× -
(4)原式=(-)×(-)×(-)×(-8)
+ 2×8× 17
在乘除运算中,小数一定要化成分数
+ ×××8
- ×××5 -
有理数乘法运算律
1-1:黑板上两个算式的结果相等吗?
相等
相等,eg:(-5)×3=3×(-5)=-15,(-2)×(-7)=(-7)×(-2)=14,……
6
× = _____
-7
× = _____
6
-7
-42
-42
1-2:把△、○中的数换成其他有理数,结果仍然相等吗?
01
课堂引入
1-1:黑板上两个算式的结果相等吗?
相等
相等,eg:[(-5)×3]×4=(-5)×(3×4)=-60,
[(-2)×(-7)]×3=(-2)×[(-7)×3]=42,……
1-2:把△、○、□中的数换成其他有理数,结果仍然相等吗?
( × ) × = _____
3
-5
3
× ( × ) = _____
-5
-2
-2
30
30
01
课堂引入
( + ) × = _____
-3
5
-3
× + × = _____
5
4
4
4
1-1:黑板上两个算式的结果相等吗?
相等
相等,eg:[(-5)+3]×2=(-5)×2+3×2=-4,
[(-2)+(-7)]×7=(-2)×7+(-7)×7=-63,……
1-2:把△、○、□中的数换成其他有理数,结果仍然相等吗?
8
8
01
课堂引入
事实上,小学里学过的乘法交换律、乘法结合律、乘法分配律,在有理数范围内仍然适用。
加法运算律
02
知识精讲
有理数乘法运算律
有理数乘法运算律:
①交换律:a×b=b×a,
②结合律:(a×b)×c=a×(b×c),
③分配律:(a+b)×c=a×c+b×c。
计算:(1)(-16)×(+2)×(-) (2)(-)×24
交换律
02
知识精讲
=+(16×2×)
=+(16××2)
=2
分配律
=×24-×24
=10-21
=-11
(3)-12×(-+)
分配律
02
知识精讲
=(-12)×+(-12)×(-)+(-12)×
=-3+8+(-2)
=3
(4)9×(-5)+(-111)×(-5)-(-2)×(-5)
=(-5)×[9+(-111)-(-2)]
=(-5)×[9+(-111)-(-2)]
=(-5)×(-100)
=500
逆用关键:取相同,合不同
02
知识精讲
分配律的逆用:
a×c+b×c=(a+b)×c。
02
知识精讲
计算:(1)16×
(2)(-10)×(-)
(3)(-)×(-)
=1
=+(10×)=1
=+(×)=1
加法运算律
02
知识精讲
倒数
一般地,如果a×b=1,那么a和b互为倒数关系,其中一个数叫作另一个数的倒数。
特别地,0没有倒数。
eg:16与,(-10)与(-),(-)与(-)…都互为倒数。
02
知识精讲
试一试:
(1)2的倒数是_______,的倒数是_______;
(2)-2的倒数是_______,-的倒数是_______;
(3)一个数的倒数是它本身的数是_______;
(4)正数的倒数是______,负数的倒数是_______。
2
±1
正数
负数
-
-
倒数
求一个数的倒数的方法 求一个整数的倒数,就是写整数分之一
求一个分数的倒数,就是调换分子和分母的位置
02
知识精讲
例1、(-8)×(-0.25)×(+125)×4
交换律、结合律同时使用
03
典例精析
解:原式
=+(8××125×4)
=+(8×125)×(×4)
=1000
例2、-6×(--+-2)
03
典例精析
解:原式
=(-6)×(-)+(-6)×(-)+(-6)×()+(-6)×(-2)
=9+4+(-5)+12
=20
例3、×(-5)+×(-3.5)+×2
03
典例精析
解:原式
=×[(-5)+(-3.5)+2]
=×(-9+2)
=-
课后总结
有理数乘法法则:
1.两数相乘,同号得正,异号得负(定号),并把绝对值相乘(定值)。
2.0与任何数相乘都得0。
3.多数相乘,
①所有因数都不为0,
当负因数有奇数个时,积为负,
当负因数有偶数个时,积为正(定号);
并把绝对值相乘(定值)。
②有一个因数为0,积就为0。
有理数乘法运算律:
①交换律:a×b=b×a,
②结合律:(a×b)×c=a×(b×c),
③分配律:(a+b)×c=a×c+b×c。
一般地,如果a×b=1,那么a和b互为倒数关系,其中一个数叫作另一个数的倒数。
特别地,0没有倒数。
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
