17.1 勾股定理 利用勾股定理作图或计算 课件(共16张PPT) 人教版 数学八年级下册
文档属性
| 名称 | 17.1 勾股定理 利用勾股定理作图或计算 课件(共16张PPT) 人教版 数学八年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1002.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-30 22:58:04 | ||
图片预览



文档简介
(共16张PPT)
17.1 勾股定理
利用勾股定理作图或计算
1.能构造直角三角形,并用勾股定理求线段长或进行一些证明.
2.运用勾股定理作出长度为无理数的线段.
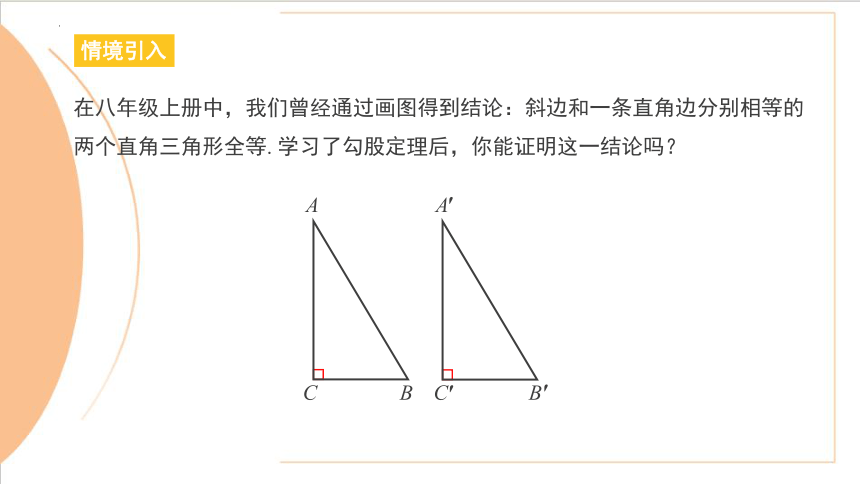
在八年级上册中,我们曾经通过画图得到结论:斜边和一条直角边分别相等的两个直角三角形全等. 学习了勾股定理后,你能证明这一结论吗?
A
B
C
A
B
C′
′
′
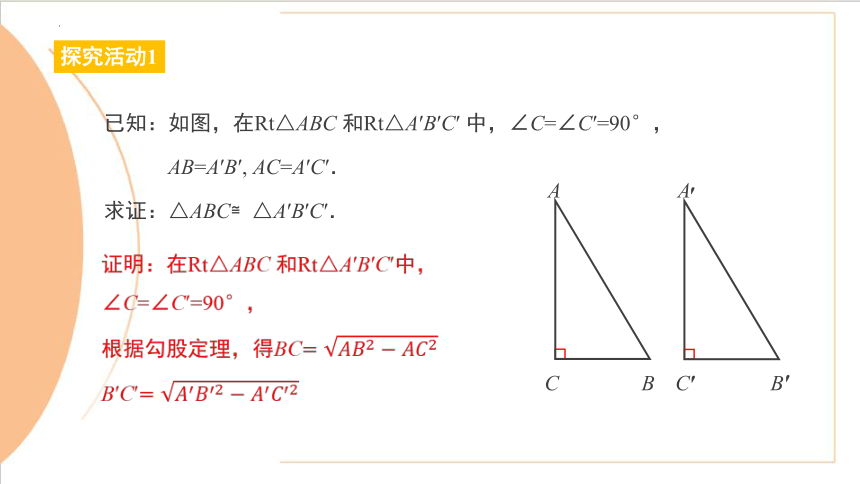
已知:如图,在Rt△ABC 和Rt△A′B′C′ 中,∠C=∠C′=90°,
AB=A′B′, AC=A′C′.
求证:△ABC≌△A′B′C′.
证明:在Rt△ABC 和Rt△A′B′C′中,∠C=∠C′=90°,
根据勾股定理,得BC
B′C′
A
B
C
A
B
C′
′
′
A
B
C
A
B
C′
′
′
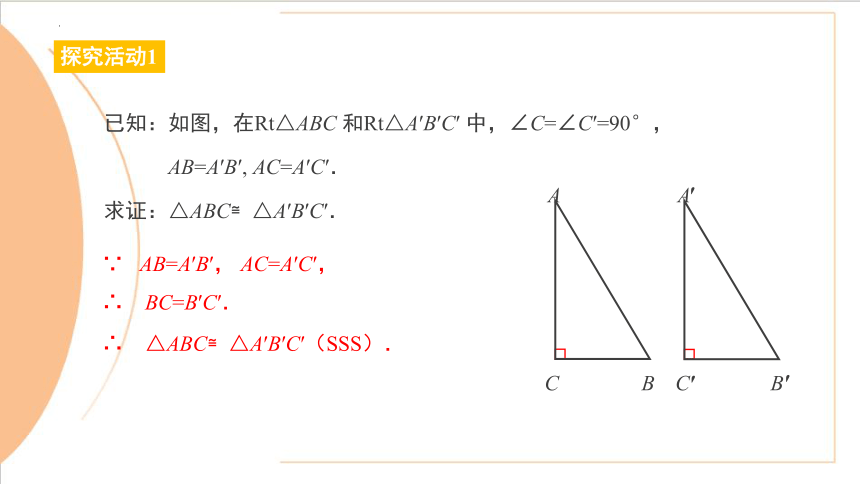
∴ △ABC≌△A′B′C′(SSS).
∵ AB=A′B′, AC=A′C′,
∴ BC=B′C′.
已知:如图,在Rt△ABC 和Rt△A′B′C′ 中,∠C=∠C′=90°,
AB=A′B′, AC=A′C′.
求证:△ABC≌△A′B′C′.
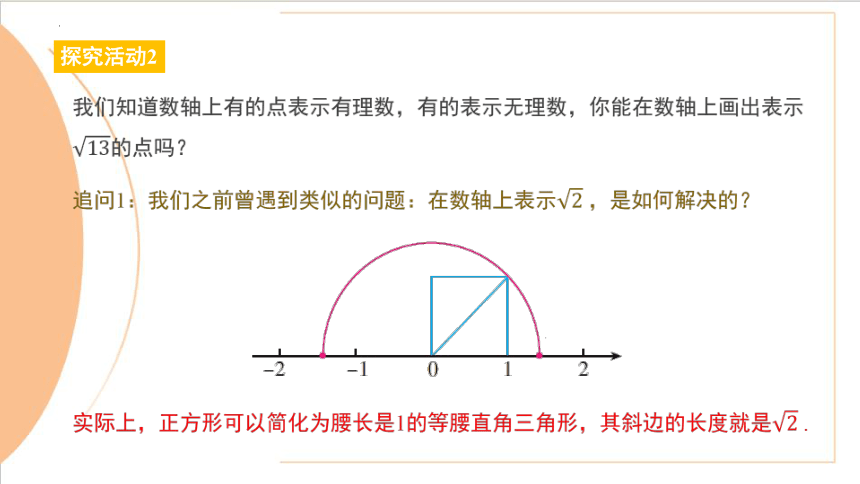
我们知道数轴上有的点表示有理数,有的表示无理数,你能在数轴上画出表示的点吗?
追问1:我们之前曾遇到类似的问题:在数轴上表示 ,是如何解决的?
实际上,正方形可以简化为腰长是1的等腰直角三角形,其斜边的长度就是 .
我们知道数轴上有的点表示有理数,有的表示无理数,你能在数轴上画出表示的点吗?
追问2:类似的,能表示为一个直角三角形斜边的长度吗?
请你试着在数轴上画出表示 的点.
作图步骤:
(1)在数轴上找出表示3的点A,则OA = 3;
(2)做直线l垂直于OA,在l上取点B,使AB = 2;
(3)以点O为圆心,以OB为半径作弧,弧与数轴的交点C即为表示的点.
“数学海螺”
实际上,借助下面的“数学海螺图”,我们可以在数轴上作出表示 的点.
如图,△ACB和△ECD都是等腰直角三角形,∠ACB =∠ECD =90°,D为AB边上一点. 求证:AD2 +DB2 =DE2.
证明:∵∠ACB =∠ECD,
∴∠ACD +∠BCD=∠ACD +∠ACE ,
∴∠BCD =∠ACE.
又BC=AC, DC=EC,
∴△ACE≌△BCD.
A
B
C
D
E
∴ ∠B =∠CAE=45°,
∠DAE =∠CAE+∠BAC=45°+45°=90°.
∴ AD2 +AE2 =DE2.
∵ AE=DB ,
∴ AD2 +DB2 =DE2.
如图,△ACB和△ECD都是等腰直角三角形,∠ACB =∠ECD =90°,D为AB边上一点. 求证:AD2 +DB2 =DE2.
A
B
C
D
E
如图,正方形ABCD中,AE垂直于BE,且AE=3,BE=4,则阴影部分的面积是( )
A.16 B.18 C.19 D.21
C
1.勾股定理有哪些方面的应用,本节课学习了勾股定理哪几方面的应用?
2.你能说说在利用勾股定理构造直角三角形解决一些相关问题方面积累了哪些经验吗?
①证明“HL”;
②在数轴上确定无理数.
1. △ABC中,AB=AC=25cm,高AD=20cm,则BC=___________,S△ABC=___________.
30cm
300cm2
2.如图,△ABC中,CD⊥AB于D,E是AC的中点,若AD=9,DE=7.5,则CD的长为___________.
12
3.如图,点C表示的数是 ( )
A.1 B. C.1.5 D.
D
下图是高空秋千的示意图,小明从起始位置点A处绕着点O经过最低点B,最终荡到最高点C处,若∠AOC=90°,点A与点B的高度差AD=1米,水平距离BD=4米,则点C与点B的高度差CE为________米.
4.5
解析:如图,作AF⊥BO于F,CG⊥BO于G,
∴BF=AD=1米,AF=BD,
∵∠AOC=∠AOF+∠COG=90°,∠AOF+∠OAF=90°,∴∠COG=∠OAF.
在△AOF与△OCG中, ,
∴△AOF≌△OCG (AAS),∴OG=AF=BD=4米.
设AO=BO=x米,在Rt△AFO中,AF2+OF2=AO2,即 42+(x-1)2=x2,解得x=8.5,则CE=GB=OB-OG=8.5-4=4.5(米).
F
G
17.1 勾股定理
利用勾股定理作图或计算
1.能构造直角三角形,并用勾股定理求线段长或进行一些证明.
2.运用勾股定理作出长度为无理数的线段.
在八年级上册中,我们曾经通过画图得到结论:斜边和一条直角边分别相等的两个直角三角形全等. 学习了勾股定理后,你能证明这一结论吗?
A
B
C
A
B
C′
′
′
已知:如图,在Rt△ABC 和Rt△A′B′C′ 中,∠C=∠C′=90°,
AB=A′B′, AC=A′C′.
求证:△ABC≌△A′B′C′.
证明:在Rt△ABC 和Rt△A′B′C′中,∠C=∠C′=90°,
根据勾股定理,得BC
B′C′
A
B
C
A
B
C′
′
′
A
B
C
A
B
C′
′
′
∴ △ABC≌△A′B′C′(SSS).
∵ AB=A′B′, AC=A′C′,
∴ BC=B′C′.
已知:如图,在Rt△ABC 和Rt△A′B′C′ 中,∠C=∠C′=90°,
AB=A′B′, AC=A′C′.
求证:△ABC≌△A′B′C′.
我们知道数轴上有的点表示有理数,有的表示无理数,你能在数轴上画出表示的点吗?
追问1:我们之前曾遇到类似的问题:在数轴上表示 ,是如何解决的?
实际上,正方形可以简化为腰长是1的等腰直角三角形,其斜边的长度就是 .
我们知道数轴上有的点表示有理数,有的表示无理数,你能在数轴上画出表示的点吗?
追问2:类似的,能表示为一个直角三角形斜边的长度吗?
请你试着在数轴上画出表示 的点.
作图步骤:
(1)在数轴上找出表示3的点A,则OA = 3;
(2)做直线l垂直于OA,在l上取点B,使AB = 2;
(3)以点O为圆心,以OB为半径作弧,弧与数轴的交点C即为表示的点.
“数学海螺”
实际上,借助下面的“数学海螺图”,我们可以在数轴上作出表示 的点.
如图,△ACB和△ECD都是等腰直角三角形,∠ACB =∠ECD =90°,D为AB边上一点. 求证:AD2 +DB2 =DE2.
证明:∵∠ACB =∠ECD,
∴∠ACD +∠BCD=∠ACD +∠ACE ,
∴∠BCD =∠ACE.
又BC=AC, DC=EC,
∴△ACE≌△BCD.
A
B
C
D
E
∴ ∠B =∠CAE=45°,
∠DAE =∠CAE+∠BAC=45°+45°=90°.
∴ AD2 +AE2 =DE2.
∵ AE=DB ,
∴ AD2 +DB2 =DE2.
如图,△ACB和△ECD都是等腰直角三角形,∠ACB =∠ECD =90°,D为AB边上一点. 求证:AD2 +DB2 =DE2.
A
B
C
D
E
如图,正方形ABCD中,AE垂直于BE,且AE=3,BE=4,则阴影部分的面积是( )
A.16 B.18 C.19 D.21
C
1.勾股定理有哪些方面的应用,本节课学习了勾股定理哪几方面的应用?
2.你能说说在利用勾股定理构造直角三角形解决一些相关问题方面积累了哪些经验吗?
①证明“HL”;
②在数轴上确定无理数.
1. △ABC中,AB=AC=25cm,高AD=20cm,则BC=___________,S△ABC=___________.
30cm
300cm2
2.如图,△ABC中,CD⊥AB于D,E是AC的中点,若AD=9,DE=7.5,则CD的长为___________.
12
3.如图,点C表示的数是 ( )
A.1 B. C.1.5 D.
D
下图是高空秋千的示意图,小明从起始位置点A处绕着点O经过最低点B,最终荡到最高点C处,若∠AOC=90°,点A与点B的高度差AD=1米,水平距离BD=4米,则点C与点B的高度差CE为________米.
4.5
解析:如图,作AF⊥BO于F,CG⊥BO于G,
∴BF=AD=1米,AF=BD,
∵∠AOC=∠AOF+∠COG=90°,∠AOF+∠OAF=90°,∴∠COG=∠OAF.
在△AOF与△OCG中, ,
∴△AOF≌△OCG (AAS),∴OG=AF=BD=4米.
设AO=BO=x米,在Rt△AFO中,AF2+OF2=AO2,即 42+(x-1)2=x2,解得x=8.5,则CE=GB=OB-OG=8.5-4=4.5(米).
F
G
