物理人教版(2019)选择性必修第一册1.2动量定理(共16张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第一册1.2动量定理(共16张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-07-30 17:41:36 | ||
图片预览






文档简介
(共16张PPT)
第一章 动量守恒定律
第2节 动量定理
有些船和码头常悬挂一些老旧轮胎,主要的用途是减轻船舶靠岸时码头与船体的撞击。这是为什么呢?
由牛顿第二定律F = ma可得
加速度:
即:F t=p –p
如图,一个质量为m的物体在光滑的水平面上受到恒力F的作用,做匀变速直线运动,在初始时刻,物体的速度为v,经过一段时间 t,它的速度为v',试推导F、 t与 p的关系。
新课讲授
F 作用了时间 t
F
F
分析与讨论
1、定义:力和力的作用时间的乘积,叫做力的冲量,用I表示
3、单位:牛·秒,符号是N·s
4、矢量性:方向由力的方向决定,若为恒定方向的力,则冲量的方向跟这力的方向相同
5、物理意义:反映了力对时间的积累效应,冲量是过程量
一、冲量
2、定义式: I=FΔt
1、内容:物体在一个过程中所受合外力的冲量等于这个过程物体的动量变化,这个关系就是动量定理
2、表达式:
3、理解:
(1)表明合外力的冲量或者是各个力冲量的矢量和是动量变化的原因
(2)动量定理是矢量式,合外力的冲量方向与物体动量变化的方向相同
二、动量定理
或
F合 t=mv – mv
I合= p
(3)动量的变化率: ,可见动量的变化率等于物体所受的合力
思考
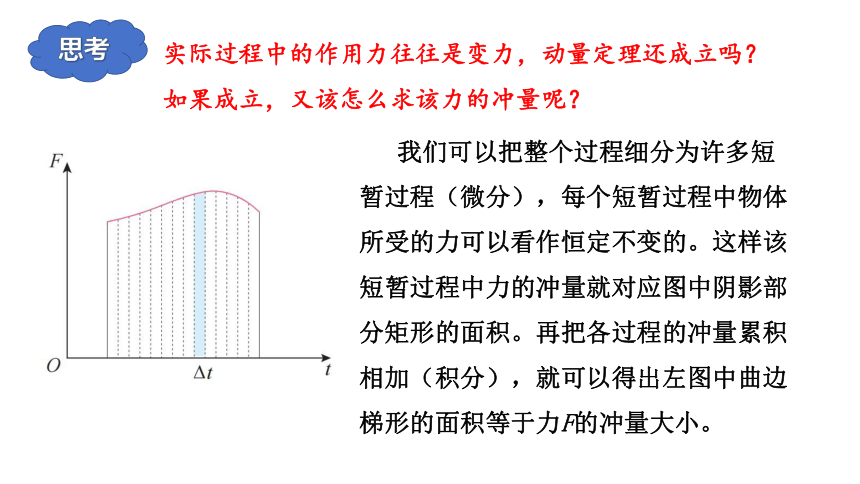
实际过程中的作用力往往是变力,动量定理还成立吗?如果成立,又该怎么求该力的冲量呢?
我们可以把整个过程细分为许多短暂过程(微分),每个短暂过程中物体所受的力可以看作恒定不变的。这样该短暂过程中力的冲量就对应图中阴影部分矩形的面积。再把各过程的冲量累积相加(积分),就可以得出左图中曲边梯形的面积等于力F的冲量大小。
ΔP一定,t短则F大,t长则F小;
由Ft=ΔP可知:
——缓冲装置
三、动量定理的应用
1、应用动量定理解释生活现象
现在你能解释一下这些轮胎的作用了吗?请你说说看!
你还能举出生活中哪些类似的例子呢?
安全头盔里的海绵
跳高比赛里的海绵垫
汽车的安全气囊
包装用的泡沫材料
做一做
将钢笔帽立在纸条上,拉动纸条,将纸带从笔帽下抽出,如何做可以让笔帽不倒?说说其中的道理!
将纸带迅速抽出,由动量定理可知,纸带对笔帽的滑动摩擦力是一个定值,作用时间t越短,则笔帽的动量变化ΔP就越小,越不容易倒
例1:如图所示,篮球运动员接传过来的篮球时,通常要先伸出双臂迎接篮球,手接触到篮球后,双手迅速后撤将篮球引至胸前。运用你所学的物理规律分析,这样做可以
A. 减小手对篮球的冲量
B. 减小篮球的动量变化量
C. 减小篮球对手的作用力
D. 缩短篮球对手的作用时间
√
例2:一个质量为0.18kg的垒球,以25m/s的水平速度飞向球棒,被球棒击打后,反向水平飞回,速度的大小为45m/s。若球棒与垒球的作用时间为0.002s,球棒对垒球平均的作用力是多大?
解:以垒球飞向球棒时的方向为正方向,
由动量定理
可得垒球所受的平均作用力为
负号表示力的方向与正方向相反,即力的方向与垒球飞来的方向相反
FΔt=mv'-mv
2、动量定理的定量计算
应用动量定理定量计算的一般步骤:
总结
例3:一物体受到方向不变的力 F 作用,其中力 F 的大小随时间变化的规律如图所示,则力 F 在6 s 内的冲量大小为
A.9 N·s B.13.5 N·s
C.15.5 N·s D.18 N·s
2、F-t图像与横轴所围的面积即为该力在这段时间内的冲量大小
总结
求变力冲量的方法
1、如果力与时间成线性关系,可以用平均力求该变力的冲量
3、利用动量定理求解:I=Δp=p'-p
√
四、流体模型
四、连续变质量问题的处理
1、流体类问题
运动着的连续的气流、水流等流体,与其它物体的表面接触的过程中,会对接触面有冲击力。此类问题通常通过动量定理来解决。
(1)正确选取研究对象:即选取很短时间Δt内动量(或其他量)发生变化的那部分流体(微元)作为研究对象。
四、流体模型
2、分析思路
(2)建立“柱状”模型:在时间Δt内通过某一横截面积为S、长度为Δl=vΔt的柱体的流体质量为Δm=ρSvΔt,以这部分质点为研究对象,研究它在Δt时间内动量(或其他量)的变化情况。
(3)根据动量定理,流体微元所受的合外力的冲量等于该流体微元动量的增量,即FΔt=ΔmΔv求解。
四、流体模型
例4:高速水流切割是一种高科技工艺加工技术,为完成飞机制造中的高难度加工特制了一台高速水流切割机器人,该机器人的喷嘴横截面积为10-7m2,喷嘴射出的水流速度为103m/s,水的密度为1×103kg/m3,设水流射到工件上后速度立即变为0。则该高速水流在工件上产生的压力大小为
A.1000 N B.100 N C.10 N D.1 N
F=100N
√
第一章 动量守恒定律
第2节 动量定理
有些船和码头常悬挂一些老旧轮胎,主要的用途是减轻船舶靠岸时码头与船体的撞击。这是为什么呢?
由牛顿第二定律F = ma可得
加速度:
即:F t=p –p
如图,一个质量为m的物体在光滑的水平面上受到恒力F的作用,做匀变速直线运动,在初始时刻,物体的速度为v,经过一段时间 t,它的速度为v',试推导F、 t与 p的关系。
新课讲授
F 作用了时间 t
F
F
分析与讨论
1、定义:力和力的作用时间的乘积,叫做力的冲量,用I表示
3、单位:牛·秒,符号是N·s
4、矢量性:方向由力的方向决定,若为恒定方向的力,则冲量的方向跟这力的方向相同
5、物理意义:反映了力对时间的积累效应,冲量是过程量
一、冲量
2、定义式: I=FΔt
1、内容:物体在一个过程中所受合外力的冲量等于这个过程物体的动量变化,这个关系就是动量定理
2、表达式:
3、理解:
(1)表明合外力的冲量或者是各个力冲量的矢量和是动量变化的原因
(2)动量定理是矢量式,合外力的冲量方向与物体动量变化的方向相同
二、动量定理
或
F合 t=mv – mv
I合= p
(3)动量的变化率: ,可见动量的变化率等于物体所受的合力
思考
实际过程中的作用力往往是变力,动量定理还成立吗?如果成立,又该怎么求该力的冲量呢?
我们可以把整个过程细分为许多短暂过程(微分),每个短暂过程中物体所受的力可以看作恒定不变的。这样该短暂过程中力的冲量就对应图中阴影部分矩形的面积。再把各过程的冲量累积相加(积分),就可以得出左图中曲边梯形的面积等于力F的冲量大小。
ΔP一定,t短则F大,t长则F小;
由Ft=ΔP可知:
——缓冲装置
三、动量定理的应用
1、应用动量定理解释生活现象
现在你能解释一下这些轮胎的作用了吗?请你说说看!
你还能举出生活中哪些类似的例子呢?
安全头盔里的海绵
跳高比赛里的海绵垫
汽车的安全气囊
包装用的泡沫材料
做一做
将钢笔帽立在纸条上,拉动纸条,将纸带从笔帽下抽出,如何做可以让笔帽不倒?说说其中的道理!
将纸带迅速抽出,由动量定理可知,纸带对笔帽的滑动摩擦力是一个定值,作用时间t越短,则笔帽的动量变化ΔP就越小,越不容易倒
例1:如图所示,篮球运动员接传过来的篮球时,通常要先伸出双臂迎接篮球,手接触到篮球后,双手迅速后撤将篮球引至胸前。运用你所学的物理规律分析,这样做可以
A. 减小手对篮球的冲量
B. 减小篮球的动量变化量
C. 减小篮球对手的作用力
D. 缩短篮球对手的作用时间
√
例2:一个质量为0.18kg的垒球,以25m/s的水平速度飞向球棒,被球棒击打后,反向水平飞回,速度的大小为45m/s。若球棒与垒球的作用时间为0.002s,球棒对垒球平均的作用力是多大?
解:以垒球飞向球棒时的方向为正方向,
由动量定理
可得垒球所受的平均作用力为
负号表示力的方向与正方向相反,即力的方向与垒球飞来的方向相反
FΔt=mv'-mv
2、动量定理的定量计算
应用动量定理定量计算的一般步骤:
总结
例3:一物体受到方向不变的力 F 作用,其中力 F 的大小随时间变化的规律如图所示,则力 F 在6 s 内的冲量大小为
A.9 N·s B.13.5 N·s
C.15.5 N·s D.18 N·s
2、F-t图像与横轴所围的面积即为该力在这段时间内的冲量大小
总结
求变力冲量的方法
1、如果力与时间成线性关系,可以用平均力求该变力的冲量
3、利用动量定理求解:I=Δp=p'-p
√
四、流体模型
四、连续变质量问题的处理
1、流体类问题
运动着的连续的气流、水流等流体,与其它物体的表面接触的过程中,会对接触面有冲击力。此类问题通常通过动量定理来解决。
(1)正确选取研究对象:即选取很短时间Δt内动量(或其他量)发生变化的那部分流体(微元)作为研究对象。
四、流体模型
2、分析思路
(2)建立“柱状”模型:在时间Δt内通过某一横截面积为S、长度为Δl=vΔt的柱体的流体质量为Δm=ρSvΔt,以这部分质点为研究对象,研究它在Δt时间内动量(或其他量)的变化情况。
(3)根据动量定理,流体微元所受的合外力的冲量等于该流体微元动量的增量,即FΔt=ΔmΔv求解。
四、流体模型
例4:高速水流切割是一种高科技工艺加工技术,为完成飞机制造中的高难度加工特制了一台高速水流切割机器人,该机器人的喷嘴横截面积为10-7m2,喷嘴射出的水流速度为103m/s,水的密度为1×103kg/m3,设水流射到工件上后速度立即变为0。则该高速水流在工件上产生的压力大小为
A.1000 N B.100 N C.10 N D.1 N
F=100N
√
