全等三角形(sas)
图片预览



文档简介
课件15张PPT。13.2 三角形全等的条件(SAS)创设情景创设情景,激发求知欲望? 某公司接到一批三角形架的加工任务,客户的要求是所有
的三角形必须全等。
质检部门为了使产品顺利过关,提出了明确的要求:
要逐一检查三角形的三条边、三个角是不是都相等。
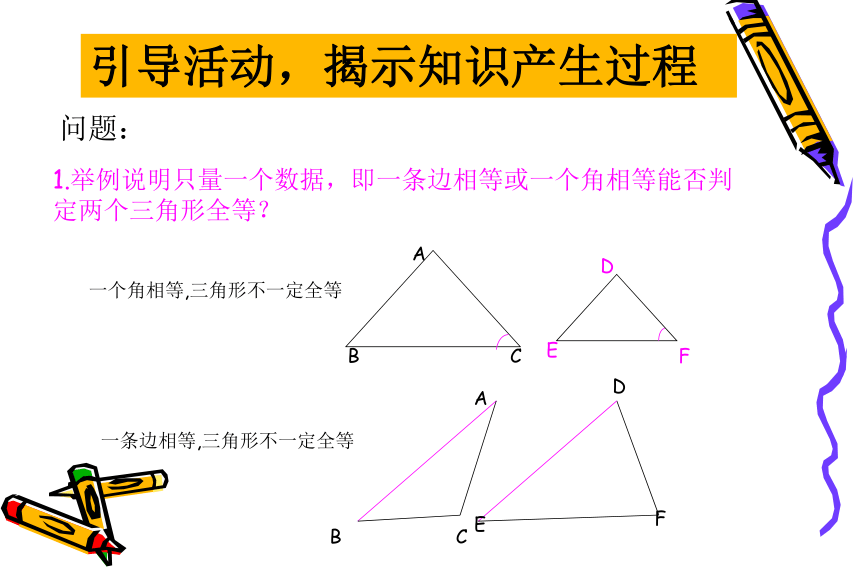
技术科的毛毛提出质疑:分别检查三条边、三个角这六个数据固然可以。 但为了提高效率,是不是可以找到一个更优化的方法,只量一个数据可以吗?两个呢?……..引导活动,揭示知识产生过程问题:1.举例说明只量一个数据,即一条边相等或一个角相等能否判定两个三角形全等?
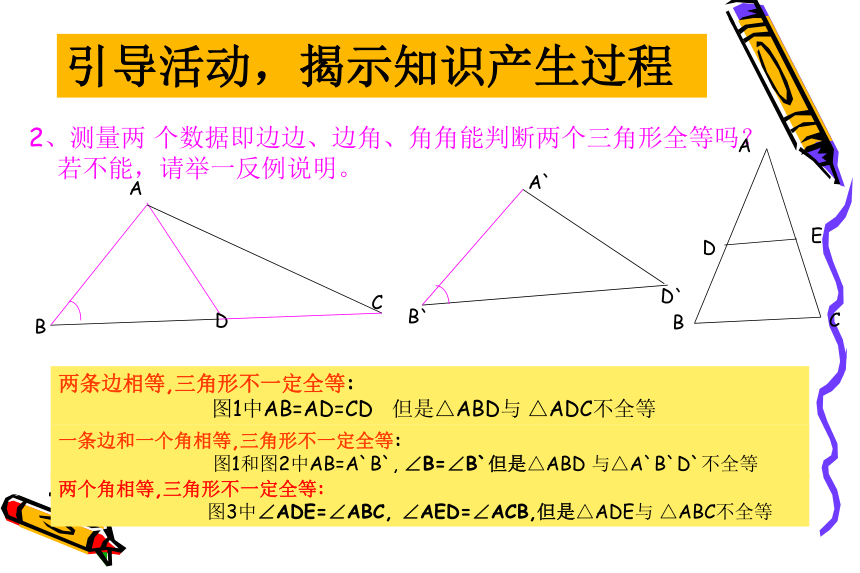
一个角相等,三角形不一定全等一条边相等,三角形不一定全等2、测量两 个数据即边边、边角、角角能判断两个三角形全等吗?若不能,请举一反例说明。
两条边相等,三角形不一定全等:
图1中AB=AD=CD 但是△ABD与 △ADC不全等 一条边和一个角相等,三角形不一定全等:
图1和图2中AB=A`B`, ∠B=∠B`但是△ABD 与△A`B`D`不全等两个角相等,三角形不一定全等:
图3中∠ADE=∠ABC, ∠AED=∠ACB,但是△ADE与 △ABC不全等引导活动,揭示知识产生过程3、讨论三个条件有哪几种情况?三个条件能否判定两个三角形全等?引导活动,揭示知识产生过程小组成果一:
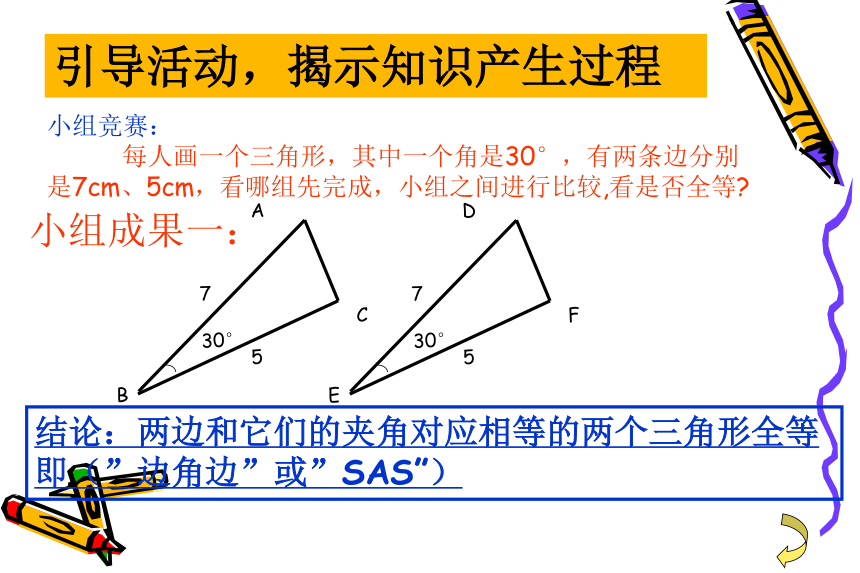
结论:两边和它们的夹角对应相等的两个三角形全等 即(”边角边”或”SAS”)引导活动,揭示知识产生过程小组竞赛:
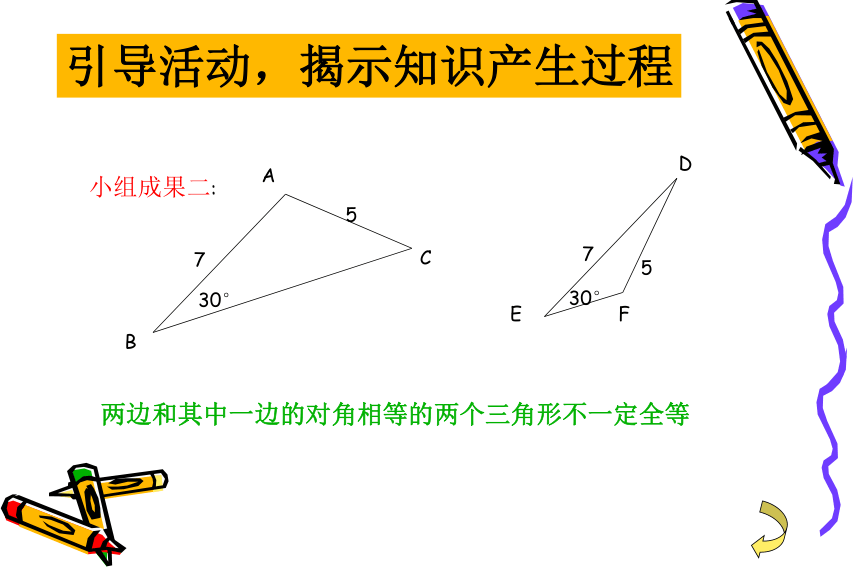
每人画一个三角形,其中一个角是30°,有两条边分别是7cm、5cm,看哪组先完成,小组之间进行比较,看是否全等?两边和其中一边的对角相等的两个三角形不一定全等引导活动,揭示知识产生过程如图,有一池塘,要测池塘两端A、B的距离,可以在平地上取一个可以直接到达A和B的点C ,连接AC并延长到D,使CD=CA,连接BC并延长到E使CE=CB连接DE,那么量出DE的长就是A、B的距离,为什么?
例题教学1、请说说本例已知了哪些条件,还差一个什么条件,怎么办?
2、你能用“因为‥‥根据‥‥所以‥‥”的表达形式说说本题的说理过程吗?
因为CA=CD(已知),CB=CE(已知), ∠1=∠2(对顶角相等)
根据两边和它们的夹角对应相等的两个三角形全等(SAS)
所以△ABC ≌ △DEC
因为△ABC ≌ △DEC
根据全等三角形对应边相等这一性质, 所以AB=DE例题教学3、 △DEC可由△ABC经过怎样的图形变换得到?方法一:△ABC顺时针旋转180度,然后平移得到△DEC
CABED12例题教学方法二:?????4、对例题进行变式与引申
已知条件不变,你能证明出AE=DB吗?
例题教学同步练习1、如图,点EF在BC上,BE=CF,AB=DC, ∠B=∠C,求证 ∠A=∠D2如图,已知AB//CD, AB=CD,要利用SAS证明△ABE ≌ △DCF,还需要添加什么条件?
同步练习课堂小结1.本节课你有什么收获?2.你还有那些疑问?
作业布置完成教材104页第3题、第4题
的三角形必须全等。
质检部门为了使产品顺利过关,提出了明确的要求:
要逐一检查三角形的三条边、三个角是不是都相等。
技术科的毛毛提出质疑:分别检查三条边、三个角这六个数据固然可以。 但为了提高效率,是不是可以找到一个更优化的方法,只量一个数据可以吗?两个呢?……..引导活动,揭示知识产生过程问题:1.举例说明只量一个数据,即一条边相等或一个角相等能否判定两个三角形全等?
一个角相等,三角形不一定全等一条边相等,三角形不一定全等2、测量两 个数据即边边、边角、角角能判断两个三角形全等吗?若不能,请举一反例说明。
两条边相等,三角形不一定全等:
图1中AB=AD=CD 但是△ABD与 △ADC不全等 一条边和一个角相等,三角形不一定全等:
图1和图2中AB=A`B`, ∠B=∠B`但是△ABD 与△A`B`D`不全等两个角相等,三角形不一定全等:
图3中∠ADE=∠ABC, ∠AED=∠ACB,但是△ADE与 △ABC不全等引导活动,揭示知识产生过程3、讨论三个条件有哪几种情况?三个条件能否判定两个三角形全等?引导活动,揭示知识产生过程小组成果一:
结论:两边和它们的夹角对应相等的两个三角形全等 即(”边角边”或”SAS”)引导活动,揭示知识产生过程小组竞赛:
每人画一个三角形,其中一个角是30°,有两条边分别是7cm、5cm,看哪组先完成,小组之间进行比较,看是否全等?两边和其中一边的对角相等的两个三角形不一定全等引导活动,揭示知识产生过程如图,有一池塘,要测池塘两端A、B的距离,可以在平地上取一个可以直接到达A和B的点C ,连接AC并延长到D,使CD=CA,连接BC并延长到E使CE=CB连接DE,那么量出DE的长就是A、B的距离,为什么?
例题教学1、请说说本例已知了哪些条件,还差一个什么条件,怎么办?
2、你能用“因为‥‥根据‥‥所以‥‥”的表达形式说说本题的说理过程吗?
因为CA=CD(已知),CB=CE(已知), ∠1=∠2(对顶角相等)
根据两边和它们的夹角对应相等的两个三角形全等(SAS)
所以△ABC ≌ △DEC
因为△ABC ≌ △DEC
根据全等三角形对应边相等这一性质, 所以AB=DE例题教学3、 △DEC可由△ABC经过怎样的图形变换得到?方法一:△ABC顺时针旋转180度,然后平移得到△DEC
CABED12例题教学方法二:?????4、对例题进行变式与引申
已知条件不变,你能证明出AE=DB吗?
例题教学同步练习1、如图,点EF在BC上,BE=CF,AB=DC, ∠B=∠C,求证 ∠A=∠D2如图,已知AB//CD, AB=CD,要利用SAS证明△ABE ≌ △DCF,还需要添加什么条件?
同步练习课堂小结1.本节课你有什么收获?2.你还有那些疑问?
作业布置完成教材104页第3题、第4题
