第3章 概率的进一步认识 测试卷(含答案)2024—2025学年北师大版数学九年级上册
文档属性
| 名称 | 第3章 概率的进一步认识 测试卷(含答案)2024—2025学年北师大版数学九年级上册 | 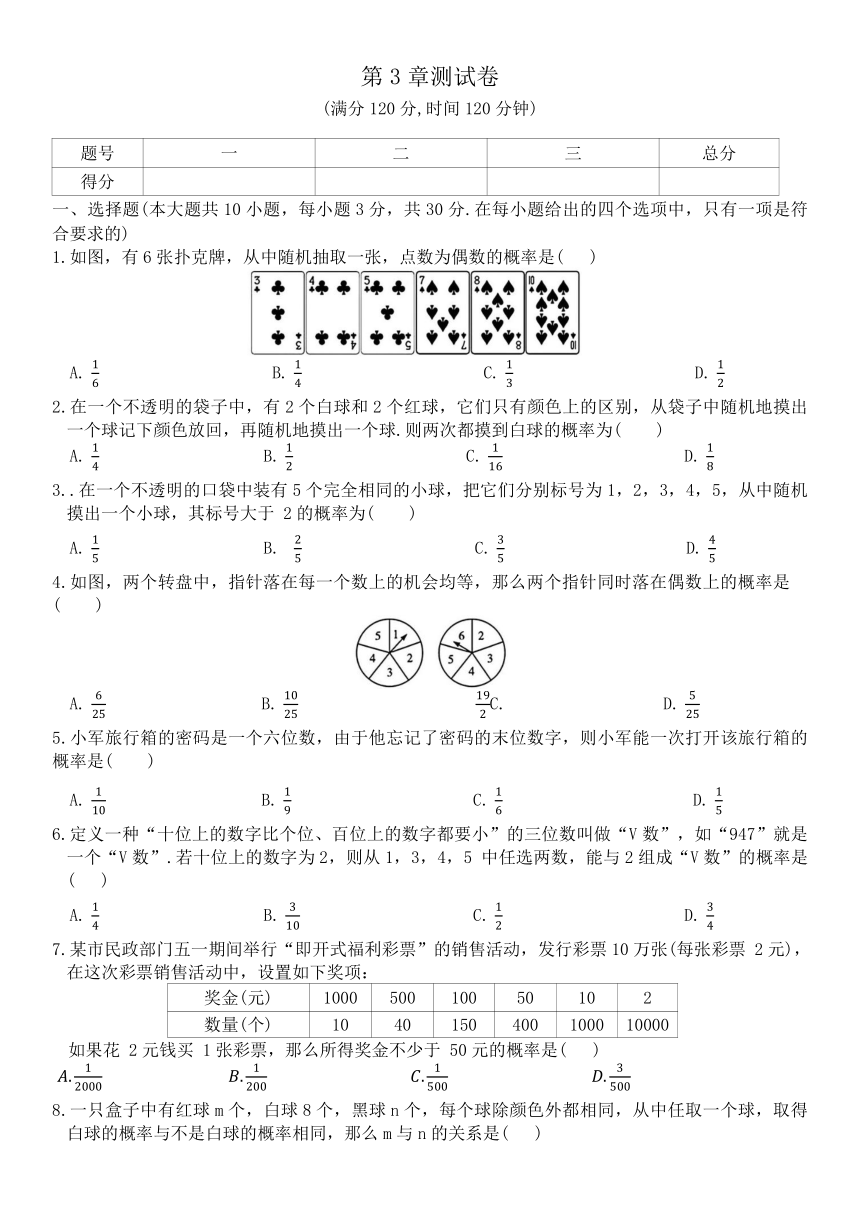 | |
| 格式 | docx | ||
| 文件大小 | 235.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-30 23:31:24 | ||
图片预览



文档简介
第3章测试卷
(满分120分,时间120分钟)
题号 一 二 三 总分
得分
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的)
1.如图,有6张扑克牌,从中随机抽取一张,点数为偶数的概率是( )
A. B. C. D.
2.在一个不透明的袋子中,有2个白球和2个红球,它们只有颜色上的区别,从袋子中随机地摸出一个球记下颜色放回,再随机地摸出一个球.则两次都摸到白球的概率为( )
A. B. C. D.
3..在一个不透明的口袋中装有5个完全相同的小球,把它们分别标号为1,2,3,4,5,从中随机摸出一个小球,其标号大于 2的概率为( )
A. B. C. D.
4.如图,两个转盘中,指针落在每一个数上的机会均等,那么两个指针同时落在偶数上的概率是 ( )
A. B. C. D.
5.小军旅行箱的密码是一个六位数,由于他忘记了密码的末位数字,则小军能一次打开该旅行箱的概率是( )
A. B. C. D.
6.定义一种“十位上的数字比个位、百位上的数字都要小”的三位数叫做“V数”,如“947”就是一个“V数”.若十位上的数字为2,则从1,3,4,5 中任选两数,能与2组成“V数”的概率是( )
A. B. C. D.
7.某市民政部门五一期间举行“即开式福利彩票”的销售活动,发行彩票10万张(每张彩票 2元),在这次彩票销售活动中,设置如下奖项:
奖金(元) 1000 500 100 50 10 2
数量(个) 10 40 150 400 1000 10000
如果花 2元钱买 1张彩票,那么所得奖金不少于 50元的概率是( )
8.一只盒子中有红球m个,白球8个,黑球n个,每个球除颜色外都相同,从中任取一个球,取得白球的概率与不是白球的概率相同,那么m与n的关系是( )
A. m+n=8 B. m+n=4 C. m=n=4 D. m=3,n=5
9.在可以不同年的条件下,下列结论叙述正确的是( )
A.400个人中至少有两人生日相同
B.300个人至少有两人生日相同
C.2个人的生日不可能相同
D.2个人的生日很有可能相同
10.航空兵空投救灾物资到指定的区域(大圆)如图所示,若要使空投物资落在中心区域(小圆)的概率为 ,则小圆与大圆的半径比值为( )
A. B. C.4 D.2
二、填空题(本大题共8小题,每小题4分,共32分,本题要求把正确结果填在规定的横线上,不需要解答过程)
11.生物学家欲调查某一地区鸟类的总数,于是他们先从该地区捕获了200只鸟作上标记后再放回,过一久后又从该地区捕获了100只鸟,在这100只鸟中,有标记的有 20只,则可估计该地区总共有 只鸟.
12.“石头、剪刀、布”是民间广为流传的游戏,游戏时,双方每次任意出“石头”、“剪刀”、“布”这三种手势中的一种,那么双方出现相同手势的概率 P= .
13.如图所示,有一电路AB是由图示的开关控制,闭合a,b,c,d,e五个开关中的任意两个,使电路形成通路.则使电路形成通路的概率是 .
14.中央电视台“幸运52”栏目中的“百宝箱”互动环节,是一种竞猜游戏,游戏规则如下:在20个商标牌中,有5个商标牌的背面注明一定的奖金额,其余商标牌的背面是一张哭脸,若翻到哭脸,就不能得奖,参与这个游戏的观众有三次翻牌机会(翻过的牌不能再翻).某观众前两次翻牌均获得若干奖金,那么他第三次翻牌获奖的概率是 .
15.甲、乙两人用两个骰子做游戏,两个骰子同时抛出,如果出现两个5点,那么甲赢;如果出现一个4 点和一个6点,那么乙赢;如果出现其他情况,那么重新抛掷.你对这个游戏公平性的评价是: .(填“公平”、“对甲有利或“对乙有利”)
16.将“定理”的英文单词theorem中的7个字母分别写在7 张相同的卡片上,字面朝下随意放在桌子上,任取一张,那么取到字母e的概率为 .
17.甲、乙两人玩猜数字游戏,游戏规则如下:有四个数字0,1,2,3,先由甲心中任选一个数字,记为m,再由乙猜甲刚才所选的数字,记为 n.若m,n满足|m-n|≤1,则称甲、乙两人“心有灵犀”.则甲、乙两人“心有灵犀”的概率是 .
18.已知a ≠0(i=1,2,…,2 012)满足 使直线 i(i=1,2,…,2 012)的图象经过一、二、四象限的a 概率是 .
三、解答题(本大题共6小题,满分58分.解答应写出文字说明、证明过程或演算步骤)
19.(8分)某小鱼塘放养鱼苗500尾,成活率为80%,成熟后,平均质量1.5斤以上的鱼为优质鱼,若在一天中随机捞出一条鱼,称出其质量,再放回去,不断重复上面的实验,共捞了50次,有32条鱼的平均质量在1.5斤以上,若优质鱼的利润为2元/斤,则这个小鱼塘在优质鱼上可获利多少元
20.(8分)某中学举行“中国梦·我的梦”演讲比赛.“志远班”的班长和学习委员都想去,于是老师制作了四张标有算式的卡片(如图所示),背面朝上洗匀后,先由班长抽一张,再由学习委员在余下的三张中抽一张.如果两张卡片上的算式都正确,班长去;如果两张卡片上的算式都错误,学习委员去;如果两张卡片上的算式一个正确一个错误,则都放回去,背面朝上洗匀后再抽.
这个游戏公平吗 请用树状图或列表的方法,结合概率予以说明.
21.(10分)我市部分学生参加了2007 年全国初中数学竞赛决赛,并取得优异成绩.已知竞赛成绩分数都是整数,试题满分为140分,参赛学生的成绩分数分布情况如下:
分数段 0—19 20—39 40—59 60—79 80—99 100—1191 120—140
人数 0 37 68 95 56 32 12
请根据以上信息解答下列问题:
(1)全市共有 人参加本次数学竞赛决赛.
(2)决赛成绩分数的中位数落在 分数段内.
(3)经竞赛组委会评定,竞赛成绩在80分以上(含 80分)的考生均可获得不同等级的奖励,求我市参加本次竞赛决赛考生的获奖比例.
22.(10分)某市体育中考现场考试内容有三项:50米跑为必测项目;另在立定跳远、实心球(二选一)和坐位体前屈、1分钟跳绳(二选一)中选择两项.
(1)每位考生有 种选择方案;
(2)用画树状图或列表的方法求小明与小刚选择同种方案的概率.(友情提醒:各种方案用A,B,C…或①,②,③…等符号来代表可简化解答过程)
23.(10分)小明在操场上做游戏,他发现地上有一个不规则的封闭图形ABD,为了知道它的面积,小明在封闭图形内画出了一个半径为1米的圆,在不远处向圈内掷石子,且记录如下:
石子落在的区域 掷石子的次数 100 200 300
石子落在⊙O内(含⊙O的边界)的次数n 28 58 93
石子落在阴影内的次数m 51 114 186
你能求出封闭图形 ABD 的面积吗
24.(12 分)如图,放在平面直角坐标系中的正方形ABCD 的边长为4,现做如下实验:抛
掷一枚均正四面体骰子(如图,它有四个顶点,各顶点数分别是1,2,3,4),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的点数作为直角坐标系中点 P 的坐标(第一次的点数为横坐标,第二次的点数为纵坐标).
(1)求点 P 落在正方形面上(含边界,下同)的概率.
(2)将正方形ABCD 平移数个单位,是否存在一种平移,使点 P 落在正方形面上的概率为 若存在,指出其中的一种平移方式;若不存在,说明理由.
第3 章测试卷
1. D 2. A 3. C 4. A 5. A 6. C 7. D 8. A 9. A 10. B11.1 00012. 14.
15.对乙有利 16. 17.
19.解∵共捞了50次,有32条鱼的平均重量在1.5斤以上,∴池塘中有1.5斤以上鱼的概率为:
故 (元),
答:优质鱼上至少可获利768元.
20.解 公平.列表如下:
A B C D
A 、 AB AC AD
B BA 、 BC BD
C CA CB CD
D DA DB DC
由表格,知共有12种等可能的结果,都正确的有BD,DB两种,都错误的有AC,CA两种,所班长去的概率为 ,学习委员去的概率为 所P(班长去)=P(学习委员去),所以这个游戏公平.
21.解(1)37+68+95+56+32+12=300(人).
所以全市共有300人参加本次数学竞赛决赛;
(2)第150个和151个数据都落在60—79分数段内,
所以决赛成绩分数的中位数落在60—79分数段内;
所以我市参加本次竞赛决赛考生的获奖比例为33.3%.
22.解 (1)4.
(2)树状图如下:
由树状图,知两人选择的方案共有16种等可能的结果,其中小明和小刚选择同种方案的有4种,所以小明与小刚选择两种方案的概率为
23.解设封闭图形ABD的面积为S,石子落在⊙O内(含⊙O的边界)的频率为n',落在阴影内的频率为m',则随试验次数的增加,m'与n'之间的关系稳定在
所以 所以S=3π.
答:估计封闭图形ABD的面积为3π平方米.
24.解(1)列表如下:由表格可知,所有等可能的情况有16种,其中点P落在正方形面上(含边界,下同)的情况有:(1,1),(2,1),(3,1),(1,2),(2,2),(3,2),(1,3),(2,3),(3,3),所以概率为
x y 1 2 3 4
1 (1,1) (2,1) (3,1) (4,1)
2 (1,2) (2,2) (3,2) (4,2)
3 (1,3) (2,3) (3,3) (4,3)
4 (1,4) (2,4) (3,4) (4,4)
(2)存在.将坐标系先向右平移一个格,再向上平移一个格,如图所示,平移后第一象限内的点有:(1,1),(2,1),(1,2),(2,2),点P落在正方形面上的概率为
(满分120分,时间120分钟)
题号 一 二 三 总分
得分
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的)
1.如图,有6张扑克牌,从中随机抽取一张,点数为偶数的概率是( )
A. B. C. D.
2.在一个不透明的袋子中,有2个白球和2个红球,它们只有颜色上的区别,从袋子中随机地摸出一个球记下颜色放回,再随机地摸出一个球.则两次都摸到白球的概率为( )
A. B. C. D.
3..在一个不透明的口袋中装有5个完全相同的小球,把它们分别标号为1,2,3,4,5,从中随机摸出一个小球,其标号大于 2的概率为( )
A. B. C. D.
4.如图,两个转盘中,指针落在每一个数上的机会均等,那么两个指针同时落在偶数上的概率是 ( )
A. B. C. D.
5.小军旅行箱的密码是一个六位数,由于他忘记了密码的末位数字,则小军能一次打开该旅行箱的概率是( )
A. B. C. D.
6.定义一种“十位上的数字比个位、百位上的数字都要小”的三位数叫做“V数”,如“947”就是一个“V数”.若十位上的数字为2,则从1,3,4,5 中任选两数,能与2组成“V数”的概率是( )
A. B. C. D.
7.某市民政部门五一期间举行“即开式福利彩票”的销售活动,发行彩票10万张(每张彩票 2元),在这次彩票销售活动中,设置如下奖项:
奖金(元) 1000 500 100 50 10 2
数量(个) 10 40 150 400 1000 10000
如果花 2元钱买 1张彩票,那么所得奖金不少于 50元的概率是( )
8.一只盒子中有红球m个,白球8个,黑球n个,每个球除颜色外都相同,从中任取一个球,取得白球的概率与不是白球的概率相同,那么m与n的关系是( )
A. m+n=8 B. m+n=4 C. m=n=4 D. m=3,n=5
9.在可以不同年的条件下,下列结论叙述正确的是( )
A.400个人中至少有两人生日相同
B.300个人至少有两人生日相同
C.2个人的生日不可能相同
D.2个人的生日很有可能相同
10.航空兵空投救灾物资到指定的区域(大圆)如图所示,若要使空投物资落在中心区域(小圆)的概率为 ,则小圆与大圆的半径比值为( )
A. B. C.4 D.2
二、填空题(本大题共8小题,每小题4分,共32分,本题要求把正确结果填在规定的横线上,不需要解答过程)
11.生物学家欲调查某一地区鸟类的总数,于是他们先从该地区捕获了200只鸟作上标记后再放回,过一久后又从该地区捕获了100只鸟,在这100只鸟中,有标记的有 20只,则可估计该地区总共有 只鸟.
12.“石头、剪刀、布”是民间广为流传的游戏,游戏时,双方每次任意出“石头”、“剪刀”、“布”这三种手势中的一种,那么双方出现相同手势的概率 P= .
13.如图所示,有一电路AB是由图示的开关控制,闭合a,b,c,d,e五个开关中的任意两个,使电路形成通路.则使电路形成通路的概率是 .
14.中央电视台“幸运52”栏目中的“百宝箱”互动环节,是一种竞猜游戏,游戏规则如下:在20个商标牌中,有5个商标牌的背面注明一定的奖金额,其余商标牌的背面是一张哭脸,若翻到哭脸,就不能得奖,参与这个游戏的观众有三次翻牌机会(翻过的牌不能再翻).某观众前两次翻牌均获得若干奖金,那么他第三次翻牌获奖的概率是 .
15.甲、乙两人用两个骰子做游戏,两个骰子同时抛出,如果出现两个5点,那么甲赢;如果出现一个4 点和一个6点,那么乙赢;如果出现其他情况,那么重新抛掷.你对这个游戏公平性的评价是: .(填“公平”、“对甲有利或“对乙有利”)
16.将“定理”的英文单词theorem中的7个字母分别写在7 张相同的卡片上,字面朝下随意放在桌子上,任取一张,那么取到字母e的概率为 .
17.甲、乙两人玩猜数字游戏,游戏规则如下:有四个数字0,1,2,3,先由甲心中任选一个数字,记为m,再由乙猜甲刚才所选的数字,记为 n.若m,n满足|m-n|≤1,则称甲、乙两人“心有灵犀”.则甲、乙两人“心有灵犀”的概率是 .
18.已知a ≠0(i=1,2,…,2 012)满足 使直线 i(i=1,2,…,2 012)的图象经过一、二、四象限的a 概率是 .
三、解答题(本大题共6小题,满分58分.解答应写出文字说明、证明过程或演算步骤)
19.(8分)某小鱼塘放养鱼苗500尾,成活率为80%,成熟后,平均质量1.5斤以上的鱼为优质鱼,若在一天中随机捞出一条鱼,称出其质量,再放回去,不断重复上面的实验,共捞了50次,有32条鱼的平均质量在1.5斤以上,若优质鱼的利润为2元/斤,则这个小鱼塘在优质鱼上可获利多少元
20.(8分)某中学举行“中国梦·我的梦”演讲比赛.“志远班”的班长和学习委员都想去,于是老师制作了四张标有算式的卡片(如图所示),背面朝上洗匀后,先由班长抽一张,再由学习委员在余下的三张中抽一张.如果两张卡片上的算式都正确,班长去;如果两张卡片上的算式都错误,学习委员去;如果两张卡片上的算式一个正确一个错误,则都放回去,背面朝上洗匀后再抽.
这个游戏公平吗 请用树状图或列表的方法,结合概率予以说明.
21.(10分)我市部分学生参加了2007 年全国初中数学竞赛决赛,并取得优异成绩.已知竞赛成绩分数都是整数,试题满分为140分,参赛学生的成绩分数分布情况如下:
分数段 0—19 20—39 40—59 60—79 80—99 100—1191 120—140
人数 0 37 68 95 56 32 12
请根据以上信息解答下列问题:
(1)全市共有 人参加本次数学竞赛决赛.
(2)决赛成绩分数的中位数落在 分数段内.
(3)经竞赛组委会评定,竞赛成绩在80分以上(含 80分)的考生均可获得不同等级的奖励,求我市参加本次竞赛决赛考生的获奖比例.
22.(10分)某市体育中考现场考试内容有三项:50米跑为必测项目;另在立定跳远、实心球(二选一)和坐位体前屈、1分钟跳绳(二选一)中选择两项.
(1)每位考生有 种选择方案;
(2)用画树状图或列表的方法求小明与小刚选择同种方案的概率.(友情提醒:各种方案用A,B,C…或①,②,③…等符号来代表可简化解答过程)
23.(10分)小明在操场上做游戏,他发现地上有一个不规则的封闭图形ABD,为了知道它的面积,小明在封闭图形内画出了一个半径为1米的圆,在不远处向圈内掷石子,且记录如下:
石子落在的区域 掷石子的次数 100 200 300
石子落在⊙O内(含⊙O的边界)的次数n 28 58 93
石子落在阴影内的次数m 51 114 186
你能求出封闭图形 ABD 的面积吗
24.(12 分)如图,放在平面直角坐标系中的正方形ABCD 的边长为4,现做如下实验:抛
掷一枚均正四面体骰子(如图,它有四个顶点,各顶点数分别是1,2,3,4),每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的点数作为直角坐标系中点 P 的坐标(第一次的点数为横坐标,第二次的点数为纵坐标).
(1)求点 P 落在正方形面上(含边界,下同)的概率.
(2)将正方形ABCD 平移数个单位,是否存在一种平移,使点 P 落在正方形面上的概率为 若存在,指出其中的一种平移方式;若不存在,说明理由.
第3 章测试卷
1. D 2. A 3. C 4. A 5. A 6. C 7. D 8. A 9. A 10. B11.1 00012. 14.
15.对乙有利 16. 17.
19.解∵共捞了50次,有32条鱼的平均重量在1.5斤以上,∴池塘中有1.5斤以上鱼的概率为:
故 (元),
答:优质鱼上至少可获利768元.
20.解 公平.列表如下:
A B C D
A 、 AB AC AD
B BA 、 BC BD
C CA CB CD
D DA DB DC
由表格,知共有12种等可能的结果,都正确的有BD,DB两种,都错误的有AC,CA两种,所班长去的概率为 ,学习委员去的概率为 所P(班长去)=P(学习委员去),所以这个游戏公平.
21.解(1)37+68+95+56+32+12=300(人).
所以全市共有300人参加本次数学竞赛决赛;
(2)第150个和151个数据都落在60—79分数段内,
所以决赛成绩分数的中位数落在60—79分数段内;
所以我市参加本次竞赛决赛考生的获奖比例为33.3%.
22.解 (1)4.
(2)树状图如下:
由树状图,知两人选择的方案共有16种等可能的结果,其中小明和小刚选择同种方案的有4种,所以小明与小刚选择两种方案的概率为
23.解设封闭图形ABD的面积为S,石子落在⊙O内(含⊙O的边界)的频率为n',落在阴影内的频率为m',则随试验次数的增加,m'与n'之间的关系稳定在
所以 所以S=3π.
答:估计封闭图形ABD的面积为3π平方米.
24.解(1)列表如下:由表格可知,所有等可能的情况有16种,其中点P落在正方形面上(含边界,下同)的情况有:(1,1),(2,1),(3,1),(1,2),(2,2),(3,2),(1,3),(2,3),(3,3),所以概率为
x y 1 2 3 4
1 (1,1) (2,1) (3,1) (4,1)
2 (1,2) (2,2) (3,2) (4,2)
3 (1,3) (2,3) (3,3) (4,3)
4 (1,4) (2,4) (3,4) (4,4)
(2)存在.将坐标系先向右平移一个格,再向上平移一个格,如图所示,平移后第一象限内的点有:(1,1),(2,1),(1,2),(2,2),点P落在正方形面上的概率为
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
