2016年华师版九年级数学下册第26章二次函数检测题含答案
文档属性
| 名称 | 2016年华师版九年级数学下册第26章二次函数检测题含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 617.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-01-04 10:59:35 | ||
图片预览


文档简介
第26章检测题
(时间:120分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.下列函数中是二次函数的是( B )
A.y=3x-1 B.y=3x2-1
C.y=(x+1)2-x2 D.y=x3+2x-3
2.若二次函数y=x2+bx+5配方后为y=(x-2)2+k,则b,k的值分别为( D )
A.0,5 B.0,1 C.-4,5 D.-4,1
3.在平面直角坐标系中,将抛物线y=x2-4先向右平移2个单位,再向上平移2个单位,得到的抛物线解析式为( B )
A.y=(x+2)2+2 B.y=(x-2)2-2
C.y=(x-2)2+2 D.y=(x+2)2-2
4.(2015·兰州)在下列二次函数中,其图象对称轴为x=-2的是( A )
A.y=(x+2)2 B.y=2x2-2 C.y=-2x2-2 D.y=2(x-2)2
5.一个二次函数的图象如图所示,则它的解析式为( B )
A.y=2(x-1)2-4 B.y=(x+1)2-4
C.y=-2(x-1)2-4 D.y=2(x+1)2-4
,第7题图) ,第8题图)
6.在同一平面直角坐标系中,一次函数y=ax+1与二次函数y=x2+a的图象可能是( C )
7.二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( B )
A.a>0 B.当-1<x<3时,y>0
C.c<0 D.当x≥1时,y随x的增大而增大
8.如图,抛物线y=x2+bx+c与x轴交于点A,B,与y轴交于点C,∠OBC=45°,则下列各式成立的是( B )
A.b-c-1=0 B.b+c+1=0 C.b-c+1=0 D.b+c-1=0
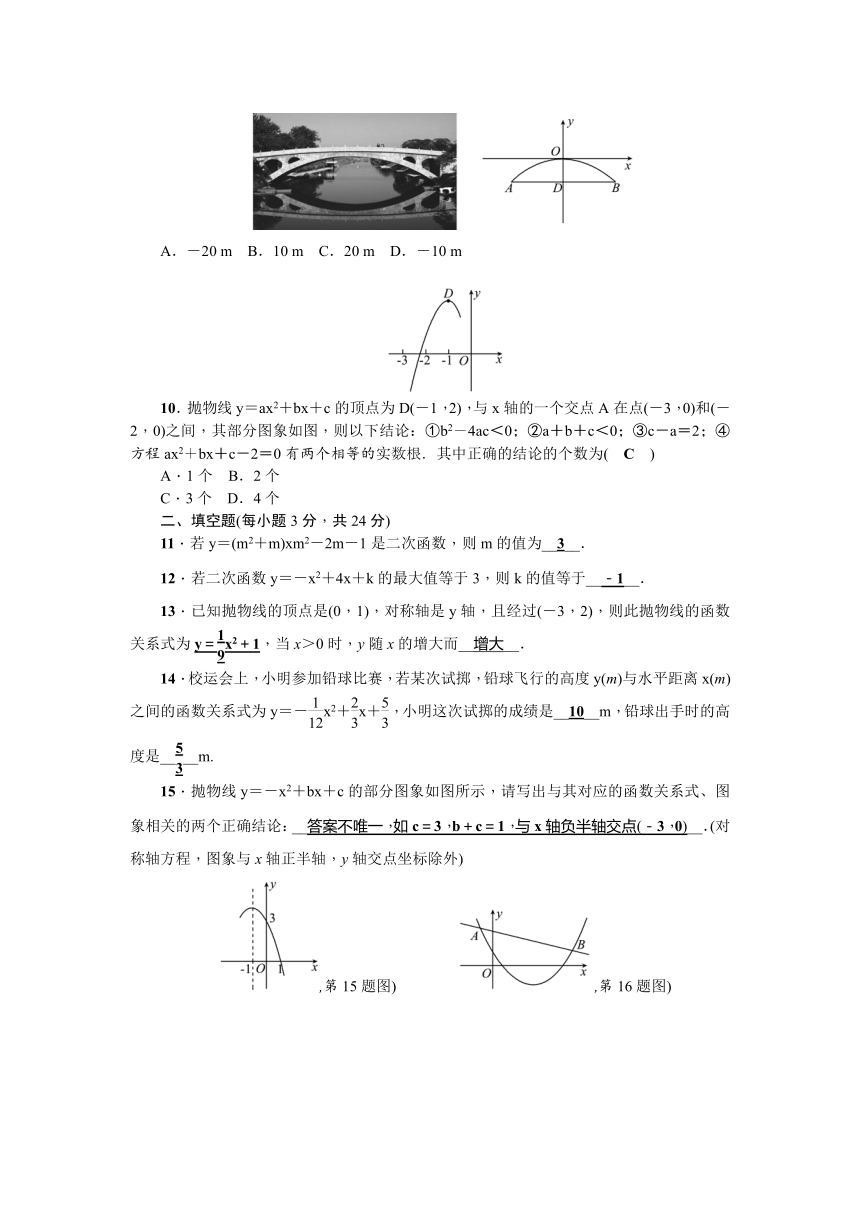
9.(2015·铜仁)河北省赵县的赵州桥 ( http: / / www.21cnjy.com )的桥拱是近似的抛物线形,建立如图所示的平面直角坐标系,其函数的关系式为y=-x2,当水面离桥拱顶的高度DO是4 m时,这时水面宽度AB为( C )
A.-20 m B.10 m C.20 m D.-10 m
10.抛物线y=ax2+bx+c的顶点为D ( http: / / www.21cnjy.com )(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:①b2-4ac<0;②a+b+c<0;③c-a=2;④方程ax2+bx+c-2=0有两个相等的实数根.其中正确的结论的个数为( C )
A.1个 B.2个
C.3个 D.4个
二、填空题(每小题3分,共24分)
11.若y=(m2+m)xm2-2m-1是二次函数,则m的值为__3__.
12.若二次函数y=-x2+4x+k的最大值等于3,则k的值等于__-1__.
13.已知抛物线的顶点是(0,1),对称轴 ( http: / / www.21cnjy.com )是y轴,且经过(-3,2),则此抛物线的函数关系式为y=x2+1,当x>0时,y随x的增大而__增大__.
14.校运会上,小明参加铅 ( http: / / www.21cnjy.com )球比赛,若某次试掷,铅球飞行的高度y(m)与水平距离x(m)之间的函数关系式为y=-x2+x+,小明这次试掷的成绩是__10__m,铅球出手时的高度是____m.
15.抛物线y=-x2+bx+c的部分 ( http: / / www.21cnjy.com )图象如图所示,请写出与其对应的函数关系式、图象相关的两个正确结论:__答案不唯一,如c=3,b+c=1,与x轴负半轴交点(-3,0)__.(对称轴方程,图象与x轴正半轴,y轴交点坐标除外)
,第15题图) ,第16题图) ,第17题图)
16.已知二次函数y1=ax2+b ( http: / / www.21cnjy.com )x+c(a≠0)与一次函数y2=kx+m(k≠0)的图象相交于点A(-2,4),B(8,2),如图所示,则使y1>y2成立的x的取值范围是__x<-2或x>8__.
17.如图,两条抛物线y1=-x2+1,y2=-x2-1与分别经过点(-2,0),(2,0)且平行于y轴的两条平行线围成的阴影部分的面积为__8__.
18.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x … -2 -1 0 1 2 …
y … 0 4 6 6 4 …
从上表可知,下列说法中正确的是__①③④__.(填写序号)
①抛物线与x轴的一个交点为(3,0);②函数y=ax2+bx+c的最大值为6;③抛物线的对称轴是x=;④在对称轴左侧,y随x增大而增大.
三、解答题(共66分)
19.(8分)已知抛物线y=a(x-h)2-4经过点(1,-3),且与抛物线y=x2的开口方向相同,形状也相同.
(1)求a,h的值;
(2)求它与x轴的交点,并画出这个二次函数图象的草图;
(3)若点A(m,y1),B(n,y2)(m<n<0)都在该抛物线上,试比较y1与y2的大小.
解:(1)a=1,h=2 (2)它与x轴的交点坐标为(0,0),(4,0),图象略 (3)y1>y2
20.(8分)如图,已知二次函数y=-x2+bx+c的图象与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,顶点D.
(1)求这个二次函数的关系式;
(2)求四边形ABDC的面积.
解:(1)y=-x2+2x+3 (2)连结O ( http: / / www.21cnjy.com )D,可求得C(0,3),D(1,4),则S四边形ABDC=S△AOC+S△COD+S△BOD=×1×3+×3×1+×3×4=9
21.(9分)已知二次函数y=x2+bx-c的图象与x轴两交点的坐标分别为(m,0),(-3m,0)(m≠0).
(1)求证:4c=3b2;
(2)若该函数图象的对称轴为直线x=1,试求二次函数的最小值.
解:(1)由题意知,m,- ( http: / / www.21cnjy.com )3m是一元二次方程x2+bx+c=0的两根,∴m+(-3m)=-b,m·(-3m)=-c,∴b=2m,c=3m2,∴4c=12m2,3b2=12m2,∴4c=3b2 (2)由题意得,-=1,∴b=-2,∴c=b2=3,∴y=x2-2x-3=(x-1)2-4,∴二次函数的最小值为-4
22.(9分)如图,正方 ( http: / / www.21cnjy.com )形ABCD的边长为4,M,N分别是BC,CD上的两个动点(M不与B,C重合),当M点在BC上运动时,保持AM和MN垂直.设BM=x,CN=y.
(1)求y与x之间函数表达式,并写出自变量x的取值范围;
(2)求出CN的最大值.
解:(1)在正方形ABCD中,AB=B ( http: / / www.21cnjy.com )C=CD=4,∠B=∠C=90°,∵AM⊥MN,∴∠AMN=90°,∴∠CMN+∠AMB=90°,在Rt△ABM中,∠MAB+∠AMB=90°,∴∠CMN=∠MAB,∴Rt△ABM∽Rt△MCN,∴=,∴=,∴y=-(x2-4x)=-(x-2)2+1(0<x<4) (2)在y=-(x-2)2+1中,当x=2时,y最大=1,∴CN的最大值为1
23.(10分)如图,四边形ABCD是菱形,点D的坐标是(0,),以点C为顶点的抛物线y=ax2+bx+c恰好经过x轴上A,B两点.
(1)求A,B,C三点的坐标;
(2)求过A,B,C三点的抛物线的解析式;
(3)若将上述抛物线沿其对称轴向上平移后恰好过D点,求平移后抛物线的解析式,并指出平移了多少个单位?
解:(1)A(1,0),B(3,0), ( http: / / www.21cnjy.com )C(2,) (2)y=-(x-2)2+ (3)设抛物线的表达式为y=-(x-2)2+k,代入D(0,),可得k=5,∴平移后的抛物线表达式为y=-(x-2)2+5,∴平移了5-=4个单位
24.(10分)某体育用品商店试销 ( http: / / www.21cnjy.com )一款成本为50元的排球,规定试销期间单价不低于成本价,且获利不得高于40%,经试销发现,销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系.
(1)试确定y与x之间的函数关系式;
(2)若该体育用品商店试销的这款排球所获 ( http: / / www.21cnjy.com )得的利润Q元,试写出利润Q(元)与销售单价x(元)之间的函数关系式;当试销单价定为多少元时,该商店获最大利润?最大利润是多少元?
(3)若该商店试销这款排球所获得的利润不低于600元,请确定销售单价x的取值范围.
解:(1)y=-x+120 (2)Q ( http: / / www.21cnjy.com )=(x-50)(-x+120)=-x2+170x-6000=-(x-85)2+1225,∴成本为50元的排球,规定试销期间单价不低于成本价,且获利不得高于40%,∴50≤x≤70,∴当试销单位定为70元时,该商店可获得最大利润,最大利润为1000元 (3)依题意-x2+170x-6000≥600,60≤x≤110,∵获利不高于40%,∴最高价格为70元,∴单价x的取值范围为60≤x≤70
25.(12分)如图,已知抛物线y=-x2+bx+c图象经过A(-1,0),B(4,0)两点.
(1)求抛物线的表达式;
(2)若C(m,m-1)是抛物线上位于 ( http: / / www.21cnjy.com )第一象限内的点,D是线段AB上的一个动点(不与A,B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.
①求证:四边形DECF是矩形;
②连结EF,线段EF的长是否存在最小值?若存在,求出EF的最小值;若不存在,请说明理由.
解:(1)y=-x2+x+2 (2)①把C(m,m-1)代入y=-x2+x+2,∴m1=3,m2=-2,∵C(m,m-1)在第一象限,∴ ∴m>-1,∴m=-2舍去,∴m=3,点C(3,2),过点C作CH⊥AB,垂足为H,则∠AHC=∠BHC=90°,由A(-1,0),B(4,0),C(3,2)得AH=4,CH=2,BH=1,AB=5,∴==2,∠AHC=∠BHC=90°,∴△AHC∽△CHB,∴∠ACH=∠CBH,∵∠CBH+∠BCH=90°,∴∠ACH+∠BCH=90°,∴∠ACB=90°,∵DE∥BC,DF∥AC,∴四边形DECF是平行四边形,∵∠ACB=90°,∴ DECF是矩形,②存在,连结CD,∵四边形DECF为矩形,∴EF=CD,当CD⊥AB时,CD的值最小,∵C(3,2),∴DC的最小值是2,EF的最小值是2
(时间:120分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.下列函数中是二次函数的是( B )
A.y=3x-1 B.y=3x2-1
C.y=(x+1)2-x2 D.y=x3+2x-3
2.若二次函数y=x2+bx+5配方后为y=(x-2)2+k,则b,k的值分别为( D )
A.0,5 B.0,1 C.-4,5 D.-4,1
3.在平面直角坐标系中,将抛物线y=x2-4先向右平移2个单位,再向上平移2个单位,得到的抛物线解析式为( B )
A.y=(x+2)2+2 B.y=(x-2)2-2
C.y=(x-2)2+2 D.y=(x+2)2-2
4.(2015·兰州)在下列二次函数中,其图象对称轴为x=-2的是( A )
A.y=(x+2)2 B.y=2x2-2 C.y=-2x2-2 D.y=2(x-2)2
5.一个二次函数的图象如图所示,则它的解析式为( B )
A.y=2(x-1)2-4 B.y=(x+1)2-4
C.y=-2(x-1)2-4 D.y=2(x+1)2-4
,第7题图) ,第8题图)
6.在同一平面直角坐标系中,一次函数y=ax+1与二次函数y=x2+a的图象可能是( C )
7.二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( B )
A.a>0 B.当-1<x<3时,y>0
C.c<0 D.当x≥1时,y随x的增大而增大
8.如图,抛物线y=x2+bx+c与x轴交于点A,B,与y轴交于点C,∠OBC=45°,则下列各式成立的是( B )
A.b-c-1=0 B.b+c+1=0 C.b-c+1=0 D.b+c-1=0
9.(2015·铜仁)河北省赵县的赵州桥 ( http: / / www.21cnjy.com )的桥拱是近似的抛物线形,建立如图所示的平面直角坐标系,其函数的关系式为y=-x2,当水面离桥拱顶的高度DO是4 m时,这时水面宽度AB为( C )
A.-20 m B.10 m C.20 m D.-10 m
10.抛物线y=ax2+bx+c的顶点为D ( http: / / www.21cnjy.com )(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论:①b2-4ac<0;②a+b+c<0;③c-a=2;④方程ax2+bx+c-2=0有两个相等的实数根.其中正确的结论的个数为( C )
A.1个 B.2个
C.3个 D.4个
二、填空题(每小题3分,共24分)
11.若y=(m2+m)xm2-2m-1是二次函数,则m的值为__3__.
12.若二次函数y=-x2+4x+k的最大值等于3,则k的值等于__-1__.
13.已知抛物线的顶点是(0,1),对称轴 ( http: / / www.21cnjy.com )是y轴,且经过(-3,2),则此抛物线的函数关系式为y=x2+1,当x>0时,y随x的增大而__增大__.
14.校运会上,小明参加铅 ( http: / / www.21cnjy.com )球比赛,若某次试掷,铅球飞行的高度y(m)与水平距离x(m)之间的函数关系式为y=-x2+x+,小明这次试掷的成绩是__10__m,铅球出手时的高度是____m.
15.抛物线y=-x2+bx+c的部分 ( http: / / www.21cnjy.com )图象如图所示,请写出与其对应的函数关系式、图象相关的两个正确结论:__答案不唯一,如c=3,b+c=1,与x轴负半轴交点(-3,0)__.(对称轴方程,图象与x轴正半轴,y轴交点坐标除外)
,第15题图) ,第16题图) ,第17题图)
16.已知二次函数y1=ax2+b ( http: / / www.21cnjy.com )x+c(a≠0)与一次函数y2=kx+m(k≠0)的图象相交于点A(-2,4),B(8,2),如图所示,则使y1>y2成立的x的取值范围是__x<-2或x>8__.
17.如图,两条抛物线y1=-x2+1,y2=-x2-1与分别经过点(-2,0),(2,0)且平行于y轴的两条平行线围成的阴影部分的面积为__8__.
18.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x … -2 -1 0 1 2 …
y … 0 4 6 6 4 …
从上表可知,下列说法中正确的是__①③④__.(填写序号)
①抛物线与x轴的一个交点为(3,0);②函数y=ax2+bx+c的最大值为6;③抛物线的对称轴是x=;④在对称轴左侧,y随x增大而增大.
三、解答题(共66分)
19.(8分)已知抛物线y=a(x-h)2-4经过点(1,-3),且与抛物线y=x2的开口方向相同,形状也相同.
(1)求a,h的值;
(2)求它与x轴的交点,并画出这个二次函数图象的草图;
(3)若点A(m,y1),B(n,y2)(m<n<0)都在该抛物线上,试比较y1与y2的大小.
解:(1)a=1,h=2 (2)它与x轴的交点坐标为(0,0),(4,0),图象略 (3)y1>y2
20.(8分)如图,已知二次函数y=-x2+bx+c的图象与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,顶点D.
(1)求这个二次函数的关系式;
(2)求四边形ABDC的面积.
解:(1)y=-x2+2x+3 (2)连结O ( http: / / www.21cnjy.com )D,可求得C(0,3),D(1,4),则S四边形ABDC=S△AOC+S△COD+S△BOD=×1×3+×3×1+×3×4=9
21.(9分)已知二次函数y=x2+bx-c的图象与x轴两交点的坐标分别为(m,0),(-3m,0)(m≠0).
(1)求证:4c=3b2;
(2)若该函数图象的对称轴为直线x=1,试求二次函数的最小值.
解:(1)由题意知,m,- ( http: / / www.21cnjy.com )3m是一元二次方程x2+bx+c=0的两根,∴m+(-3m)=-b,m·(-3m)=-c,∴b=2m,c=3m2,∴4c=12m2,3b2=12m2,∴4c=3b2 (2)由题意得,-=1,∴b=-2,∴c=b2=3,∴y=x2-2x-3=(x-1)2-4,∴二次函数的最小值为-4
22.(9分)如图,正方 ( http: / / www.21cnjy.com )形ABCD的边长为4,M,N分别是BC,CD上的两个动点(M不与B,C重合),当M点在BC上运动时,保持AM和MN垂直.设BM=x,CN=y.
(1)求y与x之间函数表达式,并写出自变量x的取值范围;
(2)求出CN的最大值.
解:(1)在正方形ABCD中,AB=B ( http: / / www.21cnjy.com )C=CD=4,∠B=∠C=90°,∵AM⊥MN,∴∠AMN=90°,∴∠CMN+∠AMB=90°,在Rt△ABM中,∠MAB+∠AMB=90°,∴∠CMN=∠MAB,∴Rt△ABM∽Rt△MCN,∴=,∴=,∴y=-(x2-4x)=-(x-2)2+1(0<x<4) (2)在y=-(x-2)2+1中,当x=2时,y最大=1,∴CN的最大值为1
23.(10分)如图,四边形ABCD是菱形,点D的坐标是(0,),以点C为顶点的抛物线y=ax2+bx+c恰好经过x轴上A,B两点.
(1)求A,B,C三点的坐标;
(2)求过A,B,C三点的抛物线的解析式;
(3)若将上述抛物线沿其对称轴向上平移后恰好过D点,求平移后抛物线的解析式,并指出平移了多少个单位?
解:(1)A(1,0),B(3,0), ( http: / / www.21cnjy.com )C(2,) (2)y=-(x-2)2+ (3)设抛物线的表达式为y=-(x-2)2+k,代入D(0,),可得k=5,∴平移后的抛物线表达式为y=-(x-2)2+5,∴平移了5-=4个单位
24.(10分)某体育用品商店试销 ( http: / / www.21cnjy.com )一款成本为50元的排球,规定试销期间单价不低于成本价,且获利不得高于40%,经试销发现,销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系.
(1)试确定y与x之间的函数关系式;
(2)若该体育用品商店试销的这款排球所获 ( http: / / www.21cnjy.com )得的利润Q元,试写出利润Q(元)与销售单价x(元)之间的函数关系式;当试销单价定为多少元时,该商店获最大利润?最大利润是多少元?
(3)若该商店试销这款排球所获得的利润不低于600元,请确定销售单价x的取值范围.
解:(1)y=-x+120 (2)Q ( http: / / www.21cnjy.com )=(x-50)(-x+120)=-x2+170x-6000=-(x-85)2+1225,∴成本为50元的排球,规定试销期间单价不低于成本价,且获利不得高于40%,∴50≤x≤70,∴当试销单位定为70元时,该商店可获得最大利润,最大利润为1000元 (3)依题意-x2+170x-6000≥600,60≤x≤110,∵获利不高于40%,∴最高价格为70元,∴单价x的取值范围为60≤x≤70
25.(12分)如图,已知抛物线y=-x2+bx+c图象经过A(-1,0),B(4,0)两点.
(1)求抛物线的表达式;
(2)若C(m,m-1)是抛物线上位于 ( http: / / www.21cnjy.com )第一象限内的点,D是线段AB上的一个动点(不与A,B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.
①求证:四边形DECF是矩形;
②连结EF,线段EF的长是否存在最小值?若存在,求出EF的最小值;若不存在,请说明理由.
解:(1)y=-x2+x+2 (2)①把C(m,m-1)代入y=-x2+x+2,∴m1=3,m2=-2,∵C(m,m-1)在第一象限,∴ ∴m>-1,∴m=-2舍去,∴m=3,点C(3,2),过点C作CH⊥AB,垂足为H,则∠AHC=∠BHC=90°,由A(-1,0),B(4,0),C(3,2)得AH=4,CH=2,BH=1,AB=5,∴==2,∠AHC=∠BHC=90°,∴△AHC∽△CHB,∴∠ACH=∠CBH,∵∠CBH+∠BCH=90°,∴∠ACH+∠BCH=90°,∴∠ACB=90°,∵DE∥BC,DF∥AC,∴四边形DECF是平行四边形,∵∠ACB=90°,∴ DECF是矩形,②存在,连结CD,∵四边形DECF为矩形,∴EF=CD,当CD⊥AB时,CD的值最小,∵C(3,2),∴DC的最小值是2,EF的最小值是2
