3.3.1 抛物线及其标准方程 课件(共22张PPT)
文档属性
| 名称 | 3.3.1 抛物线及其标准方程 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-30 22:05:59 | ||
图片预览





文档简介
(共22张PPT)
抛物线及其标准方程
请同学们思考一个问题
我们对抛物线已有了哪些认识?
新课导入
y
x
o
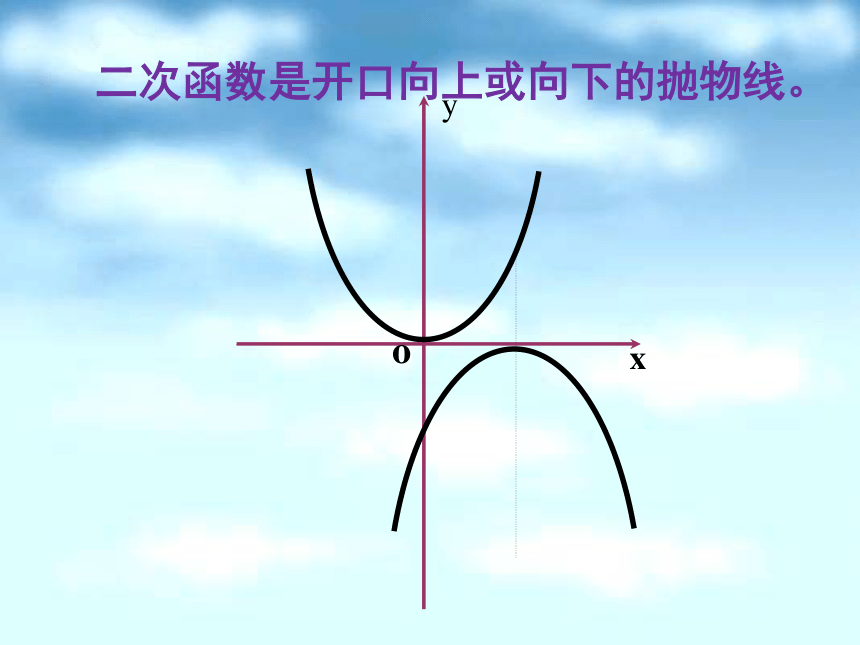
二次函数是开口向上或向下的抛物线。
生活中存在着各种形式的抛物线
抛物线的生活实例
投篮运动
抛物线的生活实例
飞机投弹
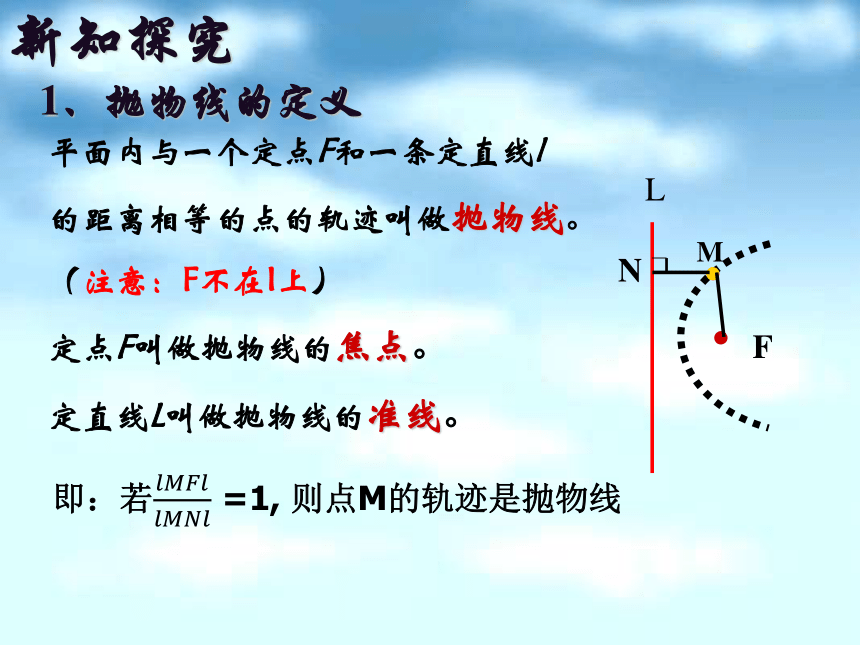
平面内与一个定点F和一条定直线l
的距离相等的点的轨迹叫做抛物线。
(注意:F不在I上)
定点F叫做抛物线的焦点。
定直线L叫做抛物线的准线。
1、抛物线的定义
·
·
F
M
L
N
新知探究
即:若 =1, 则点M的轨迹是抛物线
·
·
F
M
l
N
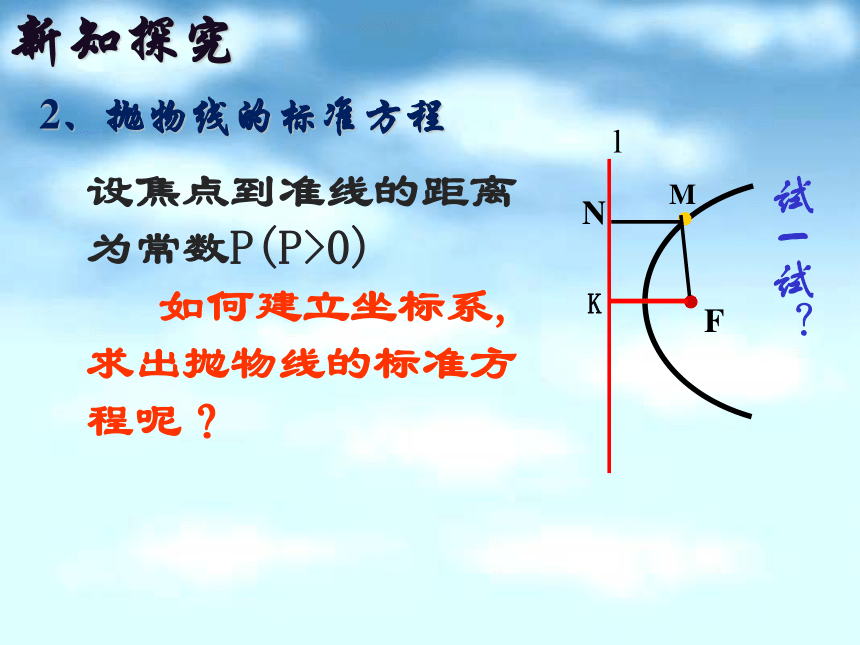
设焦点到准线的距离为常数P(P>0)
如何建立坐标系,求出抛物线的标准方程呢?
试一试?
K
2、抛物线的标准方程
新知探究
x
y
o
·
·
F
M
l
N
K
设︱KF︱= p
则F( ,0),L:x = -
p
2
p
2
设动点M的坐标为(x,y)
由抛物线的定义可知,
化简得 y2 = 2px(p>0)
2
如图,取过焦点F且垂直于准线L的直线为x轴,线段KF的中垂线为y轴
( p> 0)
2、抛物线的标准方程
方程 y2 = 2px(p>0)
叫做抛物线的标准方程
其中 p 为正常数,它的几何意义是:
焦 点 到 准 线 的 距 离
y
x
o
﹒
2、抛物线的标准方程
即右焦点F( ,0)
左准线L:x = -
p
2
p
2
但是,对于一条抛物线,它在坐标平面内的位置可以不同,所以建立的坐标系也不同,所得抛物线的方程也不同,所以抛物线的标准方程还有其它形式。
方程 y2 = 2px(p>0)
表示的抛物线,其焦点位于X轴的正半轴上,其准线交于X轴的负半轴
y
x
o
﹒
2、抛物线的标准方程
抛物线的标准方程还有哪些形式
其它形式的抛物线的焦点与准线呢?
想一想?
2、抛物线的标准方程
﹒
y
x
o
y
x
o
﹒
y
x
o
﹒
向右
向左
向上
向下
y
x
o
﹒
2、抛物线的标准方程
怎样把抛物线的位置特征(标准位置)和方程特征(标准方程)统一起来?
2、抛物线的标准方程
﹒
y
x
o
y
x
o
﹒
y
x
o
﹒
y
x
o
﹒
抛物线方程
左右型
标准方程为
y2 =+ 2px
(p>0)
开口向右:
y2 =2px(x≥ 0)
开口向左:
y2 = -2px(x≤ 0)
标准方程为
x2 =+ 2py
(p>0)
开口向上:
x2 =2py (y≥ 0)
开口向下:
x2 = -2py (y≤0)
上下型
2、抛物线的标准方程
例1:求下列抛物线的焦点坐标和准线方程:
(1)y2 = 20x (2)y=2x2
(3)2y2 +5x =0 (4)x2 +8y =0
焦点坐标 准线方程
(1 )
(2)
(3)
(4)
(5,0)
x= -5
(0,—)
1
8
y= - —
1
8
8
x= —
5
(- —,0)
5
8
(0,-2)
y=2
师生共研
注意:求抛物线的焦点一定要先把抛物线化为标准形式
例2:根据下列条件,写出抛物线的标准方程:
(1)焦点是F(-2,0)
(2)准线方程 是x =
(3)焦点到准线的距离是2
师生共研
解 (1) y2 =-8x
(2) y2 =x
(3) y2 =4x或y2 = -4x
或x2 =4y或x2 = -4y
1.由于抛物线的标准方程有四种形式,且每一种形式中都只含一个系数p,因此只要给出确定p的一个条件,就可以求出抛物线的标准方程 .
2.当抛物线的焦点坐标或准线方程给定以后,它的标准方程就唯一确定了;
若抛物线的焦点坐标或准线方程没有给定,则所求的标准方程就会有多解.
归纳
先定位,后定量
求过点A(-3,2)的抛物线的标准方程。
.
A
O
y
x
课堂练习
解:1)设抛物线的标准方程为x2=2py
把A(-3,2)代入得p=
2)设抛物线的标准方程为y2=2px
把A(-3,2)代入得p=
所以抛物线的标准方程为x2=y 或y2=-
x
3。抛物线的标准方程类型与图象特征的
对应关系及判断方法
2。抛物线的标准方程与其焦点、准线
4。注重数形结合的思想
1。抛物线的定义
课堂小结
5。注重分类讨论的思想
已知抛物线方程为x=ay2(a≠0),讨论抛物线的开口方向、焦点坐标和准线方程?
课后练习
解:抛物线的方程化为:y2=x,即2p=
当a>0时,=a,抛物线的开口向右
焦点坐标是(a,0) 准线方程是x=-a
当a<0时,=a,抛物线的开口向左
焦点坐标是(-a,0) 准线方程是x=a
谢 谢 !
抛物线及其标准方程
请同学们思考一个问题
我们对抛物线已有了哪些认识?
新课导入
y
x
o
二次函数是开口向上或向下的抛物线。
生活中存在着各种形式的抛物线
抛物线的生活实例
投篮运动
抛物线的生活实例
飞机投弹
平面内与一个定点F和一条定直线l
的距离相等的点的轨迹叫做抛物线。
(注意:F不在I上)
定点F叫做抛物线的焦点。
定直线L叫做抛物线的准线。
1、抛物线的定义
·
·
F
M
L
N
新知探究
即:若 =1, 则点M的轨迹是抛物线
·
·
F
M
l
N
设焦点到准线的距离为常数P(P>0)
如何建立坐标系,求出抛物线的标准方程呢?
试一试?
K
2、抛物线的标准方程
新知探究
x
y
o
·
·
F
M
l
N
K
设︱KF︱= p
则F( ,0),L:x = -
p
2
p
2
设动点M的坐标为(x,y)
由抛物线的定义可知,
化简得 y2 = 2px(p>0)
2
如图,取过焦点F且垂直于准线L的直线为x轴,线段KF的中垂线为y轴
( p> 0)
2、抛物线的标准方程
方程 y2 = 2px(p>0)
叫做抛物线的标准方程
其中 p 为正常数,它的几何意义是:
焦 点 到 准 线 的 距 离
y
x
o
﹒
2、抛物线的标准方程
即右焦点F( ,0)
左准线L:x = -
p
2
p
2
但是,对于一条抛物线,它在坐标平面内的位置可以不同,所以建立的坐标系也不同,所得抛物线的方程也不同,所以抛物线的标准方程还有其它形式。
方程 y2 = 2px(p>0)
表示的抛物线,其焦点位于X轴的正半轴上,其准线交于X轴的负半轴
y
x
o
﹒
2、抛物线的标准方程
抛物线的标准方程还有哪些形式
其它形式的抛物线的焦点与准线呢?
想一想?
2、抛物线的标准方程
﹒
y
x
o
y
x
o
﹒
y
x
o
﹒
向右
向左
向上
向下
y
x
o
﹒
2、抛物线的标准方程
怎样把抛物线的位置特征(标准位置)和方程特征(标准方程)统一起来?
2、抛物线的标准方程
﹒
y
x
o
y
x
o
﹒
y
x
o
﹒
y
x
o
﹒
抛物线方程
左右型
标准方程为
y2 =+ 2px
(p>0)
开口向右:
y2 =2px(x≥ 0)
开口向左:
y2 = -2px(x≤ 0)
标准方程为
x2 =+ 2py
(p>0)
开口向上:
x2 =2py (y≥ 0)
开口向下:
x2 = -2py (y≤0)
上下型
2、抛物线的标准方程
例1:求下列抛物线的焦点坐标和准线方程:
(1)y2 = 20x (2)y=2x2
(3)2y2 +5x =0 (4)x2 +8y =0
焦点坐标 准线方程
(1 )
(2)
(3)
(4)
(5,0)
x= -5
(0,—)
1
8
y= - —
1
8
8
x= —
5
(- —,0)
5
8
(0,-2)
y=2
师生共研
注意:求抛物线的焦点一定要先把抛物线化为标准形式
例2:根据下列条件,写出抛物线的标准方程:
(1)焦点是F(-2,0)
(2)准线方程 是x =
(3)焦点到准线的距离是2
师生共研
解 (1) y2 =-8x
(2) y2 =x
(3) y2 =4x或y2 = -4x
或x2 =4y或x2 = -4y
1.由于抛物线的标准方程有四种形式,且每一种形式中都只含一个系数p,因此只要给出确定p的一个条件,就可以求出抛物线的标准方程 .
2.当抛物线的焦点坐标或准线方程给定以后,它的标准方程就唯一确定了;
若抛物线的焦点坐标或准线方程没有给定,则所求的标准方程就会有多解.
归纳
先定位,后定量
求过点A(-3,2)的抛物线的标准方程。
.
A
O
y
x
课堂练习
解:1)设抛物线的标准方程为x2=2py
把A(-3,2)代入得p=
2)设抛物线的标准方程为y2=2px
把A(-3,2)代入得p=
所以抛物线的标准方程为x2=y 或y2=-
x
3。抛物线的标准方程类型与图象特征的
对应关系及判断方法
2。抛物线的标准方程与其焦点、准线
4。注重数形结合的思想
1。抛物线的定义
课堂小结
5。注重分类讨论的思想
已知抛物线方程为x=ay2(a≠0),讨论抛物线的开口方向、焦点坐标和准线方程?
课后练习
解:抛物线的方程化为:y2=x,即2p=
当a>0时,=a,抛物线的开口向右
焦点坐标是(a,0) 准线方程是x=-a
当a<0时,=a,抛物线的开口向左
焦点坐标是(-a,0) 准线方程是x=a
谢 谢 !
