有理数的乘法
图片预览






文档简介
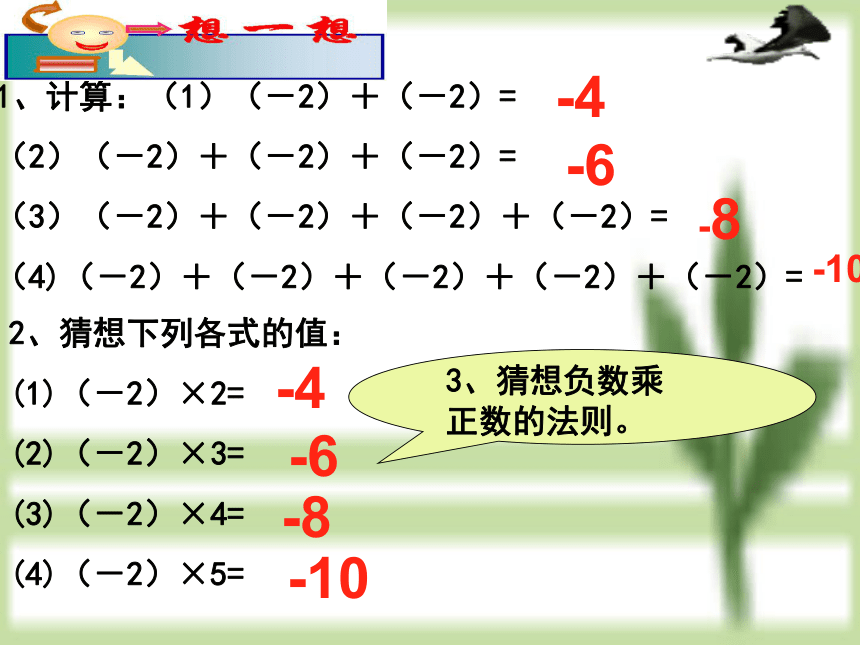
课件24张PPT。请跟我一起走进数学的这里是知识的乐园海洋殿堂这里也是一个数字的慈云中学:吴利春有理数的乘法1、计算:(1)(-2)+(-2)=
(2)(-2)+(-2)+(-2)=
(3)(-2)+(-2)+(-2)+(-2)=
(4)(-2)+(-2)+(-2)+(-2)+(-2)=2、猜想下列各式的值:
(1)(-2)×2=
(2)(-2)×3=
(3)(-2)×4=
(4)(-2)×5=3、猜想负数乘正数的法则。-4-6-10-8-10-8-6-4有关有理数的乘法到底是 怎么回事呀?接下来就让我们赶紧去研究研究吧……实例:如下图所示,一只蜗牛沿直线L爬行,它的位置恰好
在L上的O点。
1.如果蜗牛一直以每分钟2cm的速度向右爬行,
3分钟后它在什么位置?
2.如果蜗牛一直以每分钟2cm的速度向左爬行,
3分钟后它在什么位置?
3.如果蜗牛一直以每分钟2cm的速度向右爬行,
3分钟前它在什么位置?
4.如果蜗牛一直以每分钟2cm的速度向左爬行,
3分钟前它在什么位置?OL二、讲授新课1.如果蜗牛一直以每分钟2cm的速度向右爬行,3分
钟后它在什么位置?用一个运算式来表示就是:(+ 2) ×(+3)=+6 ①那么这里的“向右2cm”记作“+ 2cm”, “3分钟后”记作“+ 3分钟”2.如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟后它在什么位置?
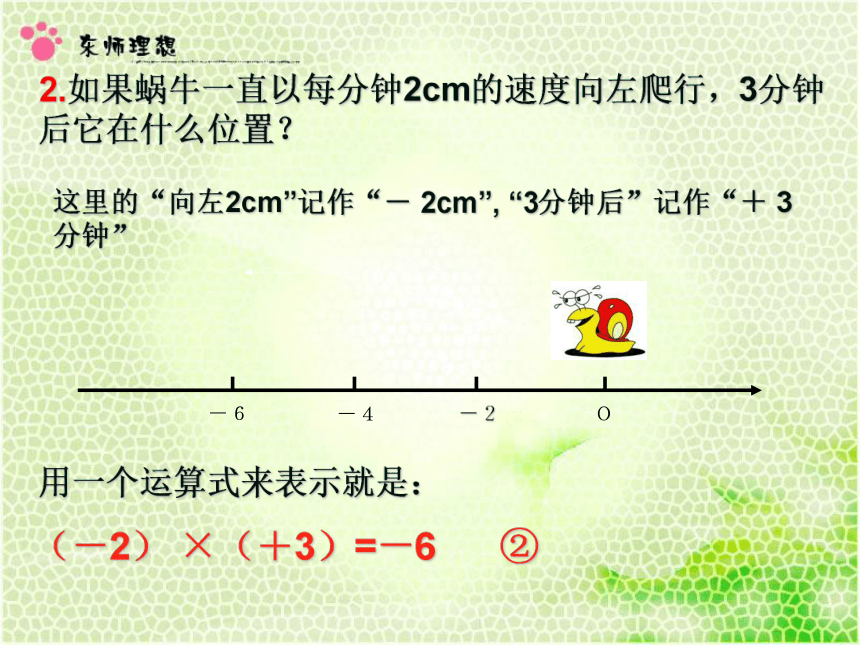
这里的“向左2cm”记作“- 2cm”, “3分钟后”记作“+ 3分钟”
用一个运算式来表示就是:
(-2) ×(+3)=-6 ②
3.如果蜗牛一直以每分钟2cm的速度向右爬行, 3分
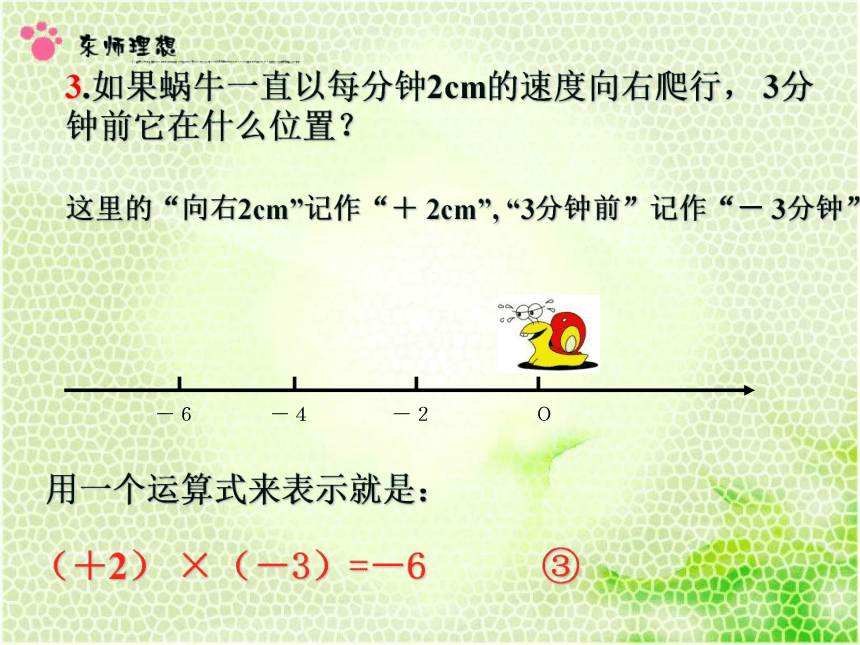
钟前它在什么位置?这里的“向右2cm”记作“+ 2cm”, “3分钟前”记作“- 3分钟”
用一个运算式来表示就是:
(+2) ×(-3)=-6 ③
4.如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟前它在什么位置?
这里的“向左2cm”记作“- 2cm”, “3分钟前”记作“- 3分钟”
用一个运算式来表示就是:(-2)×(-3)=+ 6 ④
由刚才的这四个问题我们就得到了下面四个算术式:
(+ 2) ×(+ 3)= + 6 ①
(- 2) ×(+ 3)= - 6 ②
(+ 2) ×(- 3)= - 6 ③
(-2 ) ×(- 3)= + 6 ④
正正负负积你能发现什么?请同学们观察①~④这四个式子,完成下面的填空:
正数乘正数积为 数。
负数乘正数积为 数。
正数乘负数积为 数。
负数乘负数积为 数。
乘积的绝对值等于各乘数绝对值的此外,我们还知道2 ×0 = 0 ,那么 -2 ×0 = ?显然, -2 ×0 = 0
有理数的乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘。也就是:任何数同零相乘,都得零。有理数的乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘。任何数同0相乘,都得0。例如:(-5) ×( -3)………… 同号两数相乘 (-5) ×( -3)= +( ) ,………… 得正 5 × 3 = 15 ,
………… 把绝对值相乘所以:(-5) ×( -3)= + 15
异号两数相乘得负把绝对值相乘进行有理数的乘法运算关键是积的符号的确定,计算时分两步进行。
第一步:确定积的符号,(在确定积的符号时要准确运用法则)
第二步:求绝对值的积。 思考:
例1、 (1) (-3) ×9 (2) (-4) ×(-5)
(5)- 2.4 ×0乘积是1的两个数互为倒数。解:=-27=1=1==0201.口答:
(1)6×(-9) (2)(-6)×(-9)
(3)(-6)×9 (4)(-6)×1
(5)(-6)×(-1) (6) 6×(-1)
(7)(-6)×0 (8)0×(-6) =-54=54=6=-6=0=-6=0=-1.5=-54=4=-=- 2.计算: 4.填空
(1)1×(-6)=______;(2)1+(-6)=_______;
(3)(-1)×6=________;(4)(-1)+6=______;
(5)(-1)×(-6)=______;(6)(-1)+(-6)=_____ 总结:一个数乘以1都等于它本身. 一个数乘以-1都等于它的相反数. -6-5-656-7例2 、用正负数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km气温的变化量为-6℃,攀登3km后,气温有什么变化?解: (-6)×3=-18答:气温下降了18 ℃.先说出积的符号,再说出积:随堂练习:开火车(1)(+12)×(-5)(2)(-25)×(-4)(4)(-0.4) ×(-8)=-60=100=3.2计算:=1=-10=0=1 解:1.写出下列各数的倒数:
1,-1, , ,5, .2.观察并讨论:
⑴0有没有倒数?
⑵一个数的倒数等于它的本身,那么这个数是_____.
⑶如果两数互为相反数(0除外),那么它们的倒数也是互为相反数吗?1或-1没有.是 的 .3.完成课本第30页第二 题判断题(对的入“T”,错的入“F”)
(1) 同号两数相乘,符号不变. ( )
(2) 异号两数相乘,取绝对值较大的因数的符号( )
(3) 两数相乘,如果积为正数,则这两个因数都为正数( )
(4) 两数相乘,如果积为负数,则这两个因数异号( )
(5) 两数相乘,如果积为0,则这两个数全为0.( )
(6) 两个数相乘,积比每一个因数都大.( )
(7) 如果ab>0,且a+b<0,则a<0,b<0. ( )
(8) 如果ab<0,则a>0,b<0. ( )
(9) 如果ab=0,则a,b中至少有一个为0. ( )FFF TF F TFT课堂小结有理数的乘法法则: 两数相乘,同号得___;异号得___;并把_______相乘.有理数相乘,先确定积的_____;再确定积的______.符号绝对值绝对值正负2. 倒数的定义
家庭作业:1.作业:P38 1.2题各任选3小题,第3题;
2.课外:预习新课,完成1.2题小结:乘积是1的两个数互为倒数。 在数学天地里,重要的不是我们知道什么,而是我们怎么知道—— 毕达哥拉斯结束寄语再见谢谢大家
(2)(-2)+(-2)+(-2)=
(3)(-2)+(-2)+(-2)+(-2)=
(4)(-2)+(-2)+(-2)+(-2)+(-2)=2、猜想下列各式的值:
(1)(-2)×2=
(2)(-2)×3=
(3)(-2)×4=
(4)(-2)×5=3、猜想负数乘正数的法则。-4-6-10-8-10-8-6-4有关有理数的乘法到底是 怎么回事呀?接下来就让我们赶紧去研究研究吧……实例:如下图所示,一只蜗牛沿直线L爬行,它的位置恰好
在L上的O点。
1.如果蜗牛一直以每分钟2cm的速度向右爬行,
3分钟后它在什么位置?
2.如果蜗牛一直以每分钟2cm的速度向左爬行,
3分钟后它在什么位置?
3.如果蜗牛一直以每分钟2cm的速度向右爬行,
3分钟前它在什么位置?
4.如果蜗牛一直以每分钟2cm的速度向左爬行,
3分钟前它在什么位置?OL二、讲授新课1.如果蜗牛一直以每分钟2cm的速度向右爬行,3分
钟后它在什么位置?用一个运算式来表示就是:(+ 2) ×(+3)=+6 ①那么这里的“向右2cm”记作“+ 2cm”, “3分钟后”记作“+ 3分钟”2.如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟后它在什么位置?
这里的“向左2cm”记作“- 2cm”, “3分钟后”记作“+ 3分钟”
用一个运算式来表示就是:
(-2) ×(+3)=-6 ②
3.如果蜗牛一直以每分钟2cm的速度向右爬行, 3分
钟前它在什么位置?这里的“向右2cm”记作“+ 2cm”, “3分钟前”记作“- 3分钟”
用一个运算式来表示就是:
(+2) ×(-3)=-6 ③
4.如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟前它在什么位置?
这里的“向左2cm”记作“- 2cm”, “3分钟前”记作“- 3分钟”
用一个运算式来表示就是:(-2)×(-3)=+ 6 ④
由刚才的这四个问题我们就得到了下面四个算术式:
(+ 2) ×(+ 3)= + 6 ①
(- 2) ×(+ 3)= - 6 ②
(+ 2) ×(- 3)= - 6 ③
(-2 ) ×(- 3)= + 6 ④
正正负负积你能发现什么?请同学们观察①~④这四个式子,完成下面的填空:
正数乘正数积为 数。
负数乘正数积为 数。
正数乘负数积为 数。
负数乘负数积为 数。
乘积的绝对值等于各乘数绝对值的此外,我们还知道2 ×0 = 0 ,那么 -2 ×0 = ?显然, -2 ×0 = 0
有理数的乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘。也就是:任何数同零相乘,都得零。有理数的乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘。任何数同0相乘,都得0。例如:(-5) ×( -3)………… 同号两数相乘 (-5) ×( -3)= +( ) ,………… 得正 5 × 3 = 15 ,
………… 把绝对值相乘所以:(-5) ×( -3)= + 15
异号两数相乘得负把绝对值相乘进行有理数的乘法运算关键是积的符号的确定,计算时分两步进行。
第一步:确定积的符号,(在确定积的符号时要准确运用法则)
第二步:求绝对值的积。 思考:
例1、 (1) (-3) ×9 (2) (-4) ×(-5)
(5)- 2.4 ×0乘积是1的两个数互为倒数。解:=-27=1=1==0201.口答:
(1)6×(-9) (2)(-6)×(-9)
(3)(-6)×9 (4)(-6)×1
(5)(-6)×(-1) (6) 6×(-1)
(7)(-6)×0 (8)0×(-6) =-54=54=6=-6=0=-6=0=-1.5=-54=4=-=- 2.计算: 4.填空
(1)1×(-6)=______;(2)1+(-6)=_______;
(3)(-1)×6=________;(4)(-1)+6=______;
(5)(-1)×(-6)=______;(6)(-1)+(-6)=_____ 总结:一个数乘以1都等于它本身. 一个数乘以-1都等于它的相反数. -6-5-656-7例2 、用正负数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km气温的变化量为-6℃,攀登3km后,气温有什么变化?解: (-6)×3=-18答:气温下降了18 ℃.先说出积的符号,再说出积:随堂练习:开火车(1)(+12)×(-5)(2)(-25)×(-4)(4)(-0.4) ×(-8)=-60=100=3.2计算:=1=-10=0=1 解:1.写出下列各数的倒数:
1,-1, , ,5, .2.观察并讨论:
⑴0有没有倒数?
⑵一个数的倒数等于它的本身,那么这个数是_____.
⑶如果两数互为相反数(0除外),那么它们的倒数也是互为相反数吗?1或-1没有.是 的 .3.完成课本第30页第二 题判断题(对的入“T”,错的入“F”)
(1) 同号两数相乘,符号不变. ( )
(2) 异号两数相乘,取绝对值较大的因数的符号( )
(3) 两数相乘,如果积为正数,则这两个因数都为正数( )
(4) 两数相乘,如果积为负数,则这两个因数异号( )
(5) 两数相乘,如果积为0,则这两个数全为0.( )
(6) 两个数相乘,积比每一个因数都大.( )
(7) 如果ab>0,且a+b<0,则a<0,b<0. ( )
(8) 如果ab<0,则a>0,b<0. ( )
(9) 如果ab=0,则a,b中至少有一个为0. ( )FFF TF F TFT课堂小结有理数的乘法法则: 两数相乘,同号得___;异号得___;并把_______相乘.有理数相乘,先确定积的_____;再确定积的______.符号绝对值绝对值正负2. 倒数的定义
家庭作业:1.作业:P38 1.2题各任选3小题,第3题;
2.课外:预习新课,完成1.2题小结:乘积是1的两个数互为倒数。 在数学天地里,重要的不是我们知道什么,而是我们怎么知道—— 毕达哥拉斯结束寄语再见谢谢大家
