2023-2024学年四川省成都市双流区七年级(下)期末数学试卷(含答案)
文档属性
| 名称 | 2023-2024学年四川省成都市双流区七年级(下)期末数学试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 728.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-30 19:57:33 | ||
图片预览



文档简介
2023-2024学年四川省成都市双流区七年级(下)期末数学试卷
一、选择题(每小题4分,共32分)每小题均有四个选项,其中只有一项符合题目要求.
1.(4分)加快建设体育强国,就是要弘扬中华体育精神.下列体育图标是轴对称图形的是( )
A. B.
C. D.
2.(4分)下列计算正确的是( )
A.a2+a3=2a5 B.a2 a3=a6
C.(3a3)2=9a6 D.5a6÷a3=5a2
3.(4分)某种细胞的直径为0.0000000627米,将0.0000000627用科学记数法表示为( )
A.6.27×10﹣8 B.62.7×10﹣8 C.6.27×10﹣9 D.62.7×10﹣9
4.(4分)若在△ABC中,若∠A:∠B:∠C=2:3:5,则△ABC是( )
A.直角三角形 B.等腰三角形
C.锐角三角形 D.钝角三角形
5.(4分)下列诗句表述的是随机事件的是( )
A.离离原上草,一岁一枯荣
B.危楼高百尺,手可摘星辰
C.会当凌绝顶,一览众山小
D.东边日出西边雨,道是无晴却有晴
6.(4分)一个等腰三角形的两边长分别是3cm和7cm,则它的周长是( )cm.
A.17 B.13 C.14或17 D.13或17
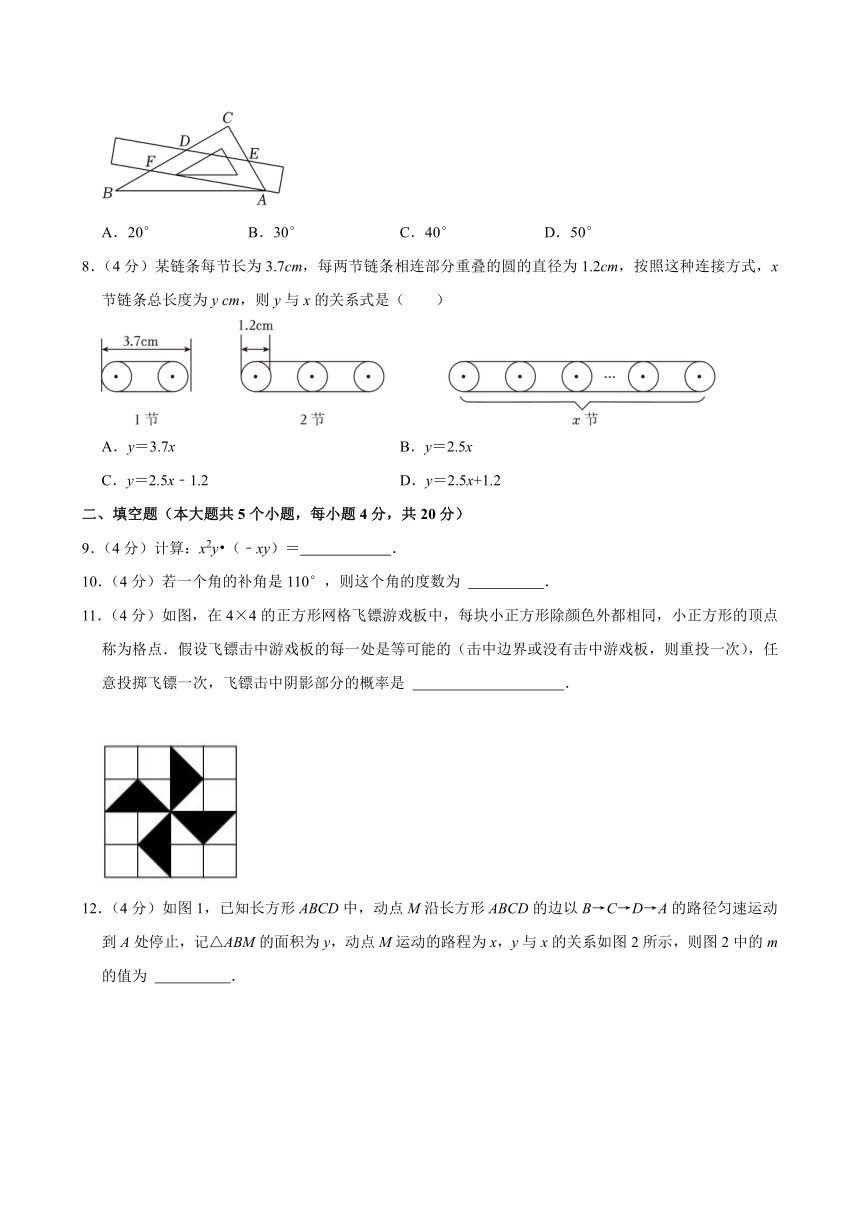
7.(4分)一把直尺和一个含30°,60°角的三角板如图所示摆放,直尺一边与三角板的两直角边分别交于F,A两点,另一边与三角板的两直角边分别交于D,E两点,且∠BAF=20°,那么∠CED的大小为( )
A.20° B.30° C.40° D.50°
8.(4分)某链条每节长为3.7cm,每两节链条相连部分重叠的圆的直径为1.2cm,按照这种连接方式,x节链条总长度为y cm,则y与x的关系式是( )
A.y=3.7x B.y=2.5x
C.y=2.5x﹣1.2 D.y=2.5x+1.2
二、填空题(本大题共5个小题,每小题4分,共20分)
9.(4分)计算:x2y (﹣xy)= .
10.(4分)若一个角的补角是110°,则这个角的度数为 .
11.(4分)如图,在4×4的正方形网格飞镖游戏板中,每块小正方形除颜色外都相同,小正方形的顶点称为格点.假设飞镖击中游戏板的每一处是等可能的(击中边界或没有击中游戏板,则重投一次),任意投掷飞镖一次,飞镖击中阴影部分的概率是 .
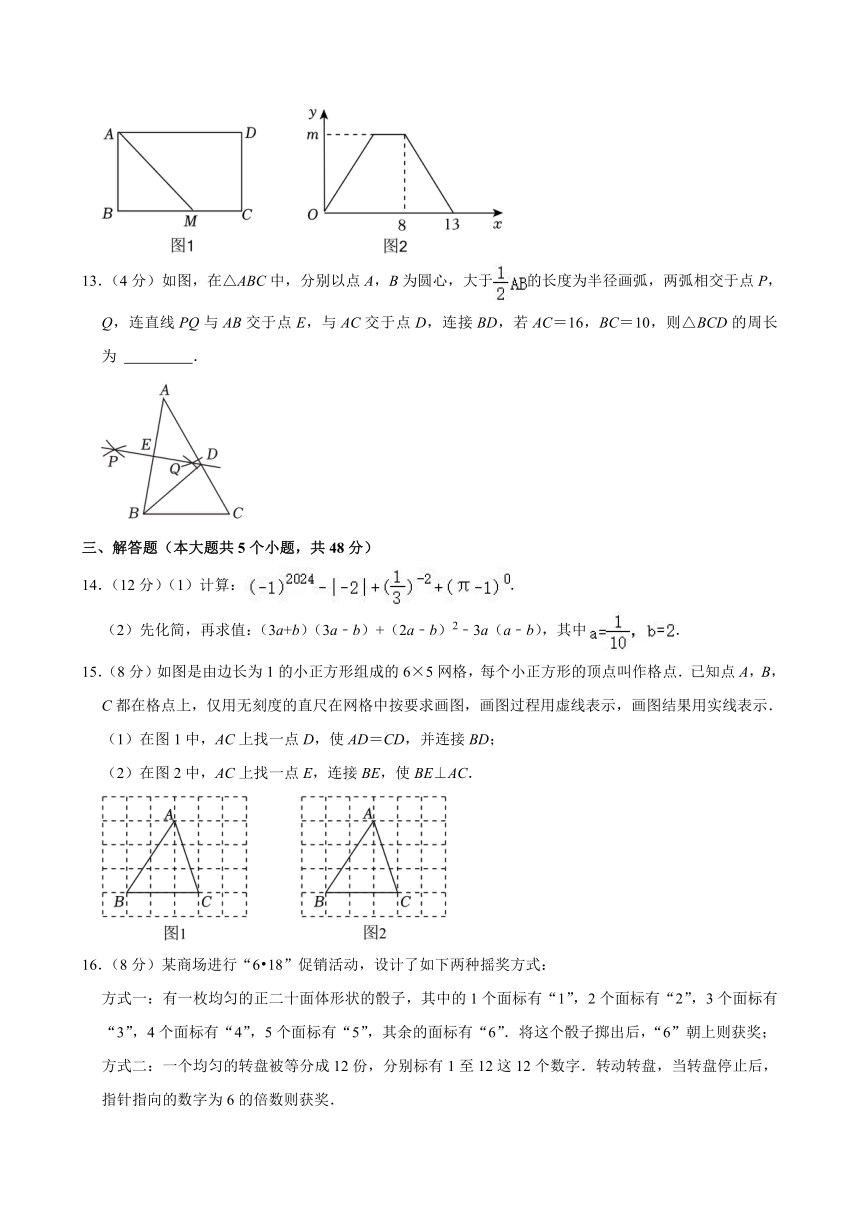
12.(4分)如图1,已知长方形ABCD中,动点M沿长方形ABCD的边以B→C→D→A的路径匀速运动到A处停止,记△ABM的面积为y,动点M运动的路程为x,y与x的关系如图2所示,则图2中的m的值为 .
13.(4分)如图,在△ABC中,分别以点A,B为圆心,大于的长度为半径画弧,两弧相交于点P,Q,连直线PQ与AB交于点E,与AC交于点D,连接BD,若AC=16,BC=10,则△BCD的周长为 .
三、解答题(本大题共5个小题,共48分)
14.(12分)(1)计算:.
(2)先化简,再求值:(3a+b)(3a﹣b)+(2a﹣b)2﹣3a(a﹣b),其中.
15.(8分)如图是由边长为1的小正方形组成的6×5网格,每个小正方形的顶点叫作格点.已知点A,B,C都在格点上,仅用无刻度的直尺在网格中按要求画图,画图过程用虚线表示,画图结果用实线表示.
(1)在图1中,AC上找一点D,使AD=CD,并连接BD;
(2)在图2中,AC上找一点E,连接BE,使BE⊥AC.
16.(8分)某商场进行“6 18”促销活动,设计了如下两种摇奖方式:
方式一:有一枚均匀的正二十面体形状的骰子,其中的1个面标有“1”,2个面标有“2”,3个面标有“3”,4个面标有“4”,5个面标有“5”,其余的面标有“6”.将这个骰子掷出后,“6”朝上则获奖;
方式二:一个均匀的转盘被等分成12份,分别标有1至12这12个数字.转动转盘,当转盘停止后,指针指向的数字为6的倍数则获奖.
(1)若采用方式一,骰子掷出后,“4”朝上的概率为 ;
(2)选择哪种摇奖方式获奖机会更大?请说明理由.
17.(10分)杆秤是我国传统的计重工具,其历史由来已久.如图,可以用秤砣到秤纽的水平距离得出秤盘上所放物体的重量.称重时,若记秤砣到秤纽的水平距离为x(厘米),秤盘所放物体重量为y(斤),其部分对应数据如表.
第1组 第2组 第3组 第4组 第5组 第6组
x(厘米) 1 3 4 6 11 12
y(斤) 0.75 1.25 1.50 2.25 3.25 3.50
(1)请判断哪一组数据是错误的?并说明理由;
(2)求当秤盘所放物体重量为5斤时秤砣到秤纽的水平距离.
18.(10分)如图,直线l1∥l2,点A,B在l1上,点C,D在l2上,连接AD,BC,AC,点M在BA的延长线上,连接CM,CM与AD交于点N.已知∠BMC=∠BCA.
(1)求证:∠BCA=∠DCN;
(2)若∠ANM=∠BAC,请判断AD,BC的位置关系,并说明理由;
(3)在(2)的条件下,连接BN,E为CD上一点,连BE与NC,AC分别交于点P,Q,且∠EBN=∠ABN.若∠ABN的度数为α,∠NCD的度数为β,∠EBC:∠NPE=2:6,请求出∠AQE的度数(结果用α,β表示).
一、填空题(本大题共5个小题,每小题4分,共20分)
19.(4分)若a+b=2,则代数式a2﹣b2+4b= .
20.(4分)一个不透明的箱子里装有红、白、黄三种颜色的小球共36个,它们除颜色外其他均相同,其中红色球有12个,黄色球的数量是白色球数量的2倍.当箱子中三种颜色的小球个数不变的情况下,要使箱子中摸出1个白色球的概率为,则应再往箱子中放入白色球 个.
21.(4分)已知关于x的多项式mx﹣n与2x2﹣3x+4的乘积结果中不含x的二次项,且常数项为﹣6,则m+n的值为 .
22.(4分)在综合实践活动中,数学兴趣小组对各边长度都是整数、最大边长为k的三角形的个数m进行了探究.发现:当k=1时,只有{1,1,1}一种情况,即m=1;当k=2时,有{1,2,2}和{2,2,2}两种情况,即m=2;当k=3时,有{1,3,3},{2,2,3},{2,3,3}和{3,3,3}四种情况,即m=4;….若k=6,则m的值为 ;若k=19,则m的值为 .
23.(4分)如图,已知四边形ABCD是长方形,以BD为直角边作等腰直角三角形BDM,且∠BDM=90°,BM交AD于点N,连接AM.若长方形ABCD的周长为14,,则△ABM的面积为 .
二、解答题(本大题共3个小题,共30分)
24.(8分)将一个边长为3a+b(b>a)的正方形进行分割,得到若干个边长为a的正方形(这类正方形记为甲型),若干个边长为b的正方形(这类正方形记为乙型),若干个邻边长为a和b的长方形(这类长方形记为丙型).
(1)若分割后,甲、乙、丙三种规格的图形都要有,且b不是a的整数倍,求分割后甲、乙、丙各类图形的个数,并画出分割示意图;
(2)若已知丙型长方形的周长为24m,面积为32m2,求分割后一个甲型正方形与一个乙型正方形的面积之和.
25.(10分)用充电器给某手机充电时,其屏幕的起始画面如图.
经测试,在用快速充电器为手机充电时,其电量E(单位:%)与充电时间t(单位:min)之间的关系如表格所示.
充电时间t(单位:min) 0 10 20 30 40 50 …
手机电量E(单位:%) 20 28 36 44 52 60 …
(1)请求出E与t之间的关系式;
(2)若电量充到76%,请求出充电时间;
(3)已知该手机正常使用时耗电量为每小时10%,在用快速充电器将其充满电后,正常使用t小时,接着再用普通充电器将其充满电,普通充电器充电平均速度为每小时15%,其“充电﹣耗电﹣充电”的时间恰好是5小时,求t的值.
26.(12分)如图1,在四边形ABCD中,BC=CD,连接AC,BD交于点O,G为OB上一点,连接CG,有CG=CO.
(1)求证:DO=BG;
(2)若∠AOD=60°,∠ACB+∠ADB=180°,求线段AO,CO,DO之间的等量关系式;
(3)如图2,在(2)的条件下,在CD上取一点E,在BC上取一点F,使CF=CE,且∠CBE+∠CAD=∠BAC,在BD上点取一点M,连接BE,FM,且∠BFM=∠DAB,试判断FM,BD的位置关系,并说明理由.
2023-2024学年四川省成都市双流区七年级(下)期末数学试卷
参考答案
一、选择题(每小题4分,共32分)每小题均有四个选项,其中只有一项符合题目要求.
1.(4分)加快建设体育强国,就是要弘扬中华体育精神.下列体育图标是轴对称图形的是( )
A. B.
C. D.
选:B.
2.(4分)下列计算正确的是( )
A.a2+a3=2a5 B.a2 a3=a6
C.(3a3)2=9a6 D.5a6÷a3=5a2
选:C.
3.(4分)某种细胞的直径为0.0000000627米,将0.0000000627用科学记数法表示为( )
A.6.27×10﹣8 B.62.7×10﹣8 C.6.27×10﹣9 D.62.7×10﹣9
选:A.
4.(4分)若在△ABC中,若∠A:∠B:∠C=2:3:5,则△ABC是( )
A.直角三角形 B.等腰三角形
C.锐角三角形 D.钝角三角形
选:A.
5.(4分)下列诗句表述的是随机事件的是( )
A.离离原上草,一岁一枯荣
B.危楼高百尺,手可摘星辰
C.会当凌绝顶,一览众山小
D.东边日出西边雨,道是无晴却有晴
选:D.
6.(4分)一个等腰三角形的两边长分别是3cm和7cm,则它的周长是( )cm.
A.17 B.13 C.14或17 D.13或17
选:A.
7.(4分)一把直尺和一个含30°,60°角的三角板如图所示摆放,直尺一边与三角板的两直角边分别交于F,A两点,另一边与三角板的两直角边分别交于D,E两点,且∠BAF=20°,那么∠CED的大小为( )
A.20° B.30° C.40° D.50°
选:C.
8.(4分)某链条每节长为3.7cm,每两节链条相连部分重叠的圆的直径为1.2cm,按照这种连接方式,x节链条总长度为y cm,则y与x的关系式是( )
A.y=3.7x B.y=2.5x
C.y=2.5x﹣1.2 D.y=2.5x+1.2
选:D.
二、填空题(本大题共5个小题,每小题4分,共20分)
9.(4分)计算:x2y (﹣xy)= ﹣x3y2 .
10.(4分)若一个角的补角是110°,则这个角的度数为 70° .
11.(4分)如图,在4×4的正方形网格飞镖游戏板中,每块小正方形除颜色外都相同,小正方形的顶点称为格点.假设飞镖击中游戏板的每一处是等可能的(击中边界或没有击中游戏板,则重投一次),任意投掷飞镖一次,飞镖击中阴影部分的概率是 .
12.(4分)如图1,已知长方形ABCD中,动点M沿长方形ABCD的边以B→C→D→A的路径匀速运动到A处停止,记△ABM的面积为y,动点M运动的路程为x,y与x的关系如图2所示,则图2中的m的值为 7.5 .
13.(4分)如图,在△ABC中,分别以点A,B为圆心,大于的长度为半径画弧,两弧相交于点P,Q,连直线PQ与AB交于点E,与AC交于点D,连接BD,若AC=16,BC=10,则△BCD的周长为 26 .
三、解答题(本大题共5个小题,共48分)
14.(12分)(1)计算:.
(2)先化简,再求值:(3a+b)(3a﹣b)+(2a﹣b)2﹣3a(a﹣b),其中.
【解答】解:(1)
=1﹣2+9+1
=9;
(2)(3a+b)(3a﹣b)+(2a﹣b)2﹣3a(a﹣b)
=9a2﹣b2+4a2﹣4ab+b2﹣3a2+3ab
=10a2﹣ab,
当时,原式=10×()2﹣×2=10×﹣=﹣=﹣.
15.(8分)如图是由边长为1的小正方形组成的6×5网格,每个小正方形的顶点叫作格点.已知点A,B,C都在格点上,仅用无刻度的直尺在网格中按要求画图,画图过程用虚线表示,画图结果用实线表示.
(1)在图1中,AC上找一点D,使AD=CD,并连接BD;
(2)在图2中,AC上找一点E,连接BE,使BE⊥AC.
【解答】解:(1)如图,点D即为所求;
(2)如图,点E即为所求.
16.(8分)某商场进行“6 18”促销活动,设计了如下两种摇奖方式:
方式一:有一枚均匀的正二十面体形状的骰子,其中的1个面标有“1”,2个面标有“2”,3个面标有“3”,4个面标有“4”,5个面标有“5”,其余的面标有“6”.将这个骰子掷出后,“6”朝上则获奖;
方式二:一个均匀的转盘被等分成12份,分别标有1至12这12个数字.转动转盘,当转盘停止后,指针指向的数字为6的倍数则获奖.
(1)若采用方式一,骰子掷出后,“4”朝上的概率为 ;
(2)选择哪种摇奖方式获奖机会更大?请说明理由.
【解答】解:(1)“4”朝上的概率是=;
故答案为:;
(2)选择摇奖方式一.
理由如下:
方式一:标有数字6的面有20﹣1﹣2﹣3﹣4﹣5=15面,
选择摇奖方式一获奖的概率为=,
方式一:数字为6的倍数的数由6,12共2个,
选择摇奖方式二获奖的概率为=,
因为>,
所以摇奖方式一获奖的机会大,选择摇奖方式一.
17.(10分)杆秤是我国传统的计重工具,其历史由来已久.如图,可以用秤砣到秤纽的水平距离得出秤盘上所放物体的重量.称重时,若记秤砣到秤纽的水平距离为x(厘米),秤盘所放物体重量为y(斤),其部分对应数据如表.
第1组 第2组 第3组 第4组 第5组 第6组
x(厘米) 1 3 4 6 11 12
y(斤) 0.75 1.25 1.50 2.25 3.25 3.50
(1)请判断哪一组数据是错误的?并说明理由;
(2)求当秤盘所放物体重量为5斤时秤砣到秤纽的水平距离.
【解答】解:(1)第4组数据是错误的.理由如下:
在图2中对6组数据描点.
可以发现,x=6,y=2.25即第4组数据是错误的.
(2)设x、y的函数关系式为y=kx+b.
将第1组和第2组数据分别代入,得,
解得,
∴x、y的函数关系式为y=0.25x+0.5.
当y=5时,有5=0.25x+0.5,解得x=18.
∴当秤盘所放物体重量为5斤时秤砣到秤纽的水平距离是18厘米.
18.(10分)如图,直线l1∥l2,点A,B在l1上,点C,D在l2上,连接AD,BC,AC,点M在BA的延长线上,连接CM,CM与AD交于点N.已知∠BMC=∠BCA.
(1)求证:∠BCA=∠DCN;
(2)若∠ANM=∠BAC,请判断AD,BC的位置关系,并说明理由;
(3)在(2)的条件下,连接BN,E为CD上一点,连BE与NC,AC分别交于点P,Q,且∠EBN=∠ABN.若∠ABN的度数为α,∠NCD的度数为β,∠EBC:∠NPE=2:6,请求出∠AQE的度数(结果用α,β表示).
【解答】(1)证明:∵l1∥l2,
∴∠BMC=∠DCN,
又∵∠BMC=∠BCA,
∴∠BCA=∠DCN;
(2)解:AD∥BC,理由如下:
∵∠BAC=∠BMC+∠ACM,
又∵∠BMC=∠BCA,
∴∠BAC=∠BCA+∠ACM=∠BCM,
∵∠ANM=∠BAC,
∴∠ANM=∠BCM,
∴AD∥BC;
(3)解:∵∠NCD的度数为β,
∴∠BCA=∠DCN=β=∠BMC,
∴∠AQE=∠BQC=180°﹣∠EBC﹣∠BCA=180°﹣∠EBC﹣β,
∵∠EBC:∠NPE=2:6,
∴∠EBC=∠NPE,
∵∠NPE=∠BMC+∠MBP=β+∠MBP,
∠MBP=∠ABN+∠EBN,
又∵∠EBN=∠ABN.∠ABN的度数为α,
∴∠MBP=α+α=2α,
∴∠NPE=β+∠MBP=β+2α,
∴∠EBC=(β+2α),
∴∠AQE=180°﹣(β+2α)﹣β=180°﹣α﹣β.
一、填空题(本大题共5个小题,每小题4分,共20分)
19.(4分)若a+b=2,则代数式a2﹣b2+4b= 4 .
【解答】解:∵a+b=2,
∴a2﹣b2+4b
=(a+b)(a﹣b)+4b
=2(a﹣b)+4b
=2a+2b=2(a+b)
=2×2
=4,
故答案为:4.
20.(4分)一个不透明的箱子里装有红、白、黄三种颜色的小球共36个,它们除颜色外其他均相同,其中红色球有12个,黄色球的数量是白色球数量的2倍.当箱子中三种颜色的小球个数不变的情况下,要使箱子中摸出1个白色球的概率为,则应再往箱子中放入白色球 6 个.
【解答】解:设箱子里装有m个白色球,
则12+m+2m=36,
解得m=8,
∴白色球有8个,
设再往箱子中放入白色球x个,
则,
解得x=6,
经检验,x=6是方程的解,
∴应再往箱子中放入白色球6个.
故答案为:6.
21.(4分)已知关于x的多项式mx﹣n与2x2﹣3x+4的乘积结果中不含x的二次项,且常数项为﹣6,则m+n的值为 .
【解答】解:(mx﹣n)(2x2﹣3x+4)=2mx3﹣(3m+2n)x2+(4m+3n)x﹣4n,
∵结果中不含x的二次项,且常数项为﹣6,
∴﹣4n=﹣6,3m+2n=0,
∴n=,m=﹣1,
∴m+n=﹣1+=.
故答案为:.
22.(4分)在综合实践活动中,数学兴趣小组对各边长度都是整数、最大边长为k的三角形的个数m进行了探究.发现:当k=1时,只有{1,1,1}一种情况,即m=1;当k=2时,有{1,2,2}和{2,2,2}两种情况,即m=2;当k=3时,有{1,3,3},{2,2,3},{2,3,3}和{3,3,3}四种情况,即m=4;….若k=6,则m的值为 12 ;若k=19,则m的值为 100 .
【解答】解:由题知,
当k=1时,m=1;
当k=2时,m=2;
当k=3时,m=4;
当k=4时,有如下情况:
{1,4,4},{2,3,4},{2,4,4},{3,3,4},{3,4,4},{4,4,4},
所以m=6,
以此类推,当k=5时,m=9;
当k=6时,m=12;
…,
因为1=1,
2=1+1,
4=1+2+1,
6=1+2+2+1,
9=1+2+3+2+1,
12=1+2+3+3+2+1,
…,
所以当k=19时,
m=1+2+3+4+5+6+7+8+9+10+9+8+7+6+5+4+3+2+1=100.
故答案为:12,100.
23.(4分)如图,已知四边形ABCD是长方形,以BD为直角边作等腰直角三角形BDM,且∠BDM=90°,BM交AD于点N,连接AM.若长方形ABCD的周长为14,,则△ABM的面积为 .
【解答】解:如图,过M作MG⊥CD交CD的延长线于点G,
∵△BDM为等腰直角三角形,
∴∠BDM=90°,DB=DM,
∴∠MDG=∠DBC=90°﹣∠BDC,
在△MGD和△DCB中,
,
∴△MGD≌△DCB(AAS),
∴DG=BC,
∵长方形ABCD的周长为14,
∴BC+CD=×14=7,
∴DG+CD=7,
∴S△ABM=S△ABN+S△ANM=AN AB+AN DG=AN (DG+AB)=××7=.
故答案为:.
二、解答题(本大题共3个小题,共30分)
24.(8分)将一个边长为3a+b(b>a)的正方形进行分割,得到若干个边长为a的正方形(这类正方形记为甲型),若干个边长为b的正方形(这类正方形记为乙型),若干个邻边长为a和b的长方形(这类长方形记为丙型).
(1)若分割后,甲、乙、丙三种规格的图形都要有,且b不是a的整数倍,求分割后甲、乙、丙各类图形的个数,并画出分割示意图;
(2)若已知丙型长方形的周长为24m,面积为32m2,求分割后一个甲型正方形与一个乙型正方形的面积之和.
【解答】解:(1)∵(3a+b)2=9a2+6ab+b2,
∴甲类图形有9个,乙类图形有1个,丙类图形有6个.
分割示意图如图所示,
(2)∵丙型长方形的周长为24m,面积为32m2,
∴a+b=12,ab=32,
a2+b2=(a+b)2﹣2ab=122﹣64=80(m2),
即分割后一个甲型正方形与一个乙型正方形的面积之和为80m2.
25.(10分)用充电器给某手机充电时,其屏幕的起始画面如图.
经测试,在用快速充电器为手机充电时,其电量E(单位:%)与充电时间t(单位:min)之间的关系如表格所示.
充电时间t(单位:min) 0 10 20 30 40 50 …
手机电量E(单位:%) 20 28 36 44 52 60 …
(1)请求出E与t之间的关系式;
(2)若电量充到76%,请求出充电时间;
(3)已知该手机正常使用时耗电量为每小时10%,在用快速充电器将其充满电后,正常使用t小时,接着再用普通充电器将其充满电,普通充电器充电平均速度为每小时15%,其“充电﹣耗电﹣充电”的时间恰好是5小时,求t的值.
【解答】解:(1)由题意得,根据表格数据函数图象过(0,20),(10,28),
设函数关系式为E=kt+b,
∴.
∴k=0.8,b=20.
∴E与t的关系式为E=0.8t+20.
(2)由题意,结合(1)E=0.8t+20,
令E=76,
∴0.8t+20=76.
∴t=70.
答:充电时间为70min.
(3)由题意得,令E=100,
∴快充充满电需要的时间为100min=h.
∴15(5﹣﹣t)=10t.
∴t=2.
26.(12分)如图1,在四边形ABCD中,BC=CD,连接AC,BD交于点O,G为OB上一点,连接CG,有CG=CO.
(1)求证:DO=BG;
(2)若∠AOD=60°,∠ACB+∠ADB=180°,求线段AO,CO,DO之间的等量关系式;
(3)如图2,在(2)的条件下,在CD上取一点E,在BC上取一点F,使CF=CE,且∠CBE+∠CAD=∠BAC,在BD上点取一点M,连接BE,FM,且∠BFM=∠DAB,试判断FM,BD的位置关系,并说明理由.
【解答】(1)证明:过C作CH⊥BD于点H,
∵CB=CD,CO=CG,
∴DH=BH,OH=GH,
∴DH﹣OH=BH﹣GH,
∴DO=BG;
(2)解:AO=DO+CO,证明如下,
方法一:在OA上取一点M,连接DM,使DM=DO,
∵∠AOD=60°,DM=DO,
∴△DOM为等边三角形,
∴DM=DO=OM,
∵CO=CG,∠COG=∠AOD=60°,
∴△COG为等边三角形,
∴∠OCG=60°,
∵∠DAO+∠AOD+∠ADB=180°,且∠ACB+∠ADB=180°,
∴∠DAO+∠AOD=∠ACB=∠OCG+∠BCG,
∵∠AOD=∠OCG=60°,
∴∠DAO=∠BCG,
由(1)中方法可得,∠DCH=∠BCH,∠OCH=∠GCH,
∴∠DCH﹣∠OCH=∠BCH﹣∠GCH,
即∠DCO=∠BCG,
∴∠DCO=∠DAO,
∵∠DMA=∠DOC=120°,
∴△DAM≌△DCO(AAS),
∴AM=OC,
∵AO=AM+OM,
∴AO=DO+CO.
方法二:如图,作DQ⊥AC于点Q,
由方法一得出DA=DC,
∴AQ=CQ,
设OQ=x,OC=y,则AQ=CQ=x+y,
∴AO=AQ+OQ=2x+y,
∵∠AOD=60°,
∴∠ODQ=30°,
∴OD﹣2OQ=2x,
∴OD+OC=2x+y=AO,
∴AO=DO+CO.
(3)解:FM⊥BD,理由如下,
如图,连接DF,
∵CB=CD,∠BCE=∠CDF,CE=CF,
∴△BCE≌△DCF(SAS),
∴∠BEC=∠DFC,∠CBE=∠CDF,
设∠ACB=α,∠BAC=β,
∵∠ACB+∠ADB=180°,
∴∠ADB=180°﹣α,
∵∠AOD=60°,
∴∠CAD=α﹣60°=∠DCA,
∴∠BCE=∠DCA+∠ACB=2α﹣60°,
∴∠CBD==120°﹣α,
∵∠CBE+∠CAD=∠BAC,
∴∠CBE=∠BAC﹣∠CAD=β﹣α+60°=∠CDF,
∵∠CEB=180°﹣∠CBE﹣∠BCE=180°﹣(β﹣α+60°)﹣(2α﹣60°)=180°﹣α﹣β,
∴∠CFD=180°﹣α﹣β,
∵∠BFM=∠DAB=∠DAC+∠BAC=α﹣60°+β,
∴∠DFM=180°﹣∠CFD﹣∠BFM=180°﹣(180°﹣α﹣β)﹣(α﹣60°+β)=60°,
由(2)得AO=DO+CO=OG+BG=OB,∠AOD=60°,
∴∠OBA=∠OAB=30°,即β=30°,
∵∠FDB=180°﹣∠CBD﹣∠BFD=180°﹣(120°﹣α)﹣(α+β)=60°﹣β=30°,
∴∠FMD=180°﹣∠FDM﹣∠DFM=90°,
∴FM⊥BD.
一、选择题(每小题4分,共32分)每小题均有四个选项,其中只有一项符合题目要求.
1.(4分)加快建设体育强国,就是要弘扬中华体育精神.下列体育图标是轴对称图形的是( )
A. B.
C. D.
2.(4分)下列计算正确的是( )
A.a2+a3=2a5 B.a2 a3=a6
C.(3a3)2=9a6 D.5a6÷a3=5a2
3.(4分)某种细胞的直径为0.0000000627米,将0.0000000627用科学记数法表示为( )
A.6.27×10﹣8 B.62.7×10﹣8 C.6.27×10﹣9 D.62.7×10﹣9
4.(4分)若在△ABC中,若∠A:∠B:∠C=2:3:5,则△ABC是( )
A.直角三角形 B.等腰三角形
C.锐角三角形 D.钝角三角形
5.(4分)下列诗句表述的是随机事件的是( )
A.离离原上草,一岁一枯荣
B.危楼高百尺,手可摘星辰
C.会当凌绝顶,一览众山小
D.东边日出西边雨,道是无晴却有晴
6.(4分)一个等腰三角形的两边长分别是3cm和7cm,则它的周长是( )cm.
A.17 B.13 C.14或17 D.13或17
7.(4分)一把直尺和一个含30°,60°角的三角板如图所示摆放,直尺一边与三角板的两直角边分别交于F,A两点,另一边与三角板的两直角边分别交于D,E两点,且∠BAF=20°,那么∠CED的大小为( )
A.20° B.30° C.40° D.50°
8.(4分)某链条每节长为3.7cm,每两节链条相连部分重叠的圆的直径为1.2cm,按照这种连接方式,x节链条总长度为y cm,则y与x的关系式是( )
A.y=3.7x B.y=2.5x
C.y=2.5x﹣1.2 D.y=2.5x+1.2
二、填空题(本大题共5个小题,每小题4分,共20分)
9.(4分)计算:x2y (﹣xy)= .
10.(4分)若一个角的补角是110°,则这个角的度数为 .
11.(4分)如图,在4×4的正方形网格飞镖游戏板中,每块小正方形除颜色外都相同,小正方形的顶点称为格点.假设飞镖击中游戏板的每一处是等可能的(击中边界或没有击中游戏板,则重投一次),任意投掷飞镖一次,飞镖击中阴影部分的概率是 .
12.(4分)如图1,已知长方形ABCD中,动点M沿长方形ABCD的边以B→C→D→A的路径匀速运动到A处停止,记△ABM的面积为y,动点M运动的路程为x,y与x的关系如图2所示,则图2中的m的值为 .
13.(4分)如图,在△ABC中,分别以点A,B为圆心,大于的长度为半径画弧,两弧相交于点P,Q,连直线PQ与AB交于点E,与AC交于点D,连接BD,若AC=16,BC=10,则△BCD的周长为 .
三、解答题(本大题共5个小题,共48分)
14.(12分)(1)计算:.
(2)先化简,再求值:(3a+b)(3a﹣b)+(2a﹣b)2﹣3a(a﹣b),其中.
15.(8分)如图是由边长为1的小正方形组成的6×5网格,每个小正方形的顶点叫作格点.已知点A,B,C都在格点上,仅用无刻度的直尺在网格中按要求画图,画图过程用虚线表示,画图结果用实线表示.
(1)在图1中,AC上找一点D,使AD=CD,并连接BD;
(2)在图2中,AC上找一点E,连接BE,使BE⊥AC.
16.(8分)某商场进行“6 18”促销活动,设计了如下两种摇奖方式:
方式一:有一枚均匀的正二十面体形状的骰子,其中的1个面标有“1”,2个面标有“2”,3个面标有“3”,4个面标有“4”,5个面标有“5”,其余的面标有“6”.将这个骰子掷出后,“6”朝上则获奖;
方式二:一个均匀的转盘被等分成12份,分别标有1至12这12个数字.转动转盘,当转盘停止后,指针指向的数字为6的倍数则获奖.
(1)若采用方式一,骰子掷出后,“4”朝上的概率为 ;
(2)选择哪种摇奖方式获奖机会更大?请说明理由.
17.(10分)杆秤是我国传统的计重工具,其历史由来已久.如图,可以用秤砣到秤纽的水平距离得出秤盘上所放物体的重量.称重时,若记秤砣到秤纽的水平距离为x(厘米),秤盘所放物体重量为y(斤),其部分对应数据如表.
第1组 第2组 第3组 第4组 第5组 第6组
x(厘米) 1 3 4 6 11 12
y(斤) 0.75 1.25 1.50 2.25 3.25 3.50
(1)请判断哪一组数据是错误的?并说明理由;
(2)求当秤盘所放物体重量为5斤时秤砣到秤纽的水平距离.
18.(10分)如图,直线l1∥l2,点A,B在l1上,点C,D在l2上,连接AD,BC,AC,点M在BA的延长线上,连接CM,CM与AD交于点N.已知∠BMC=∠BCA.
(1)求证:∠BCA=∠DCN;
(2)若∠ANM=∠BAC,请判断AD,BC的位置关系,并说明理由;
(3)在(2)的条件下,连接BN,E为CD上一点,连BE与NC,AC分别交于点P,Q,且∠EBN=∠ABN.若∠ABN的度数为α,∠NCD的度数为β,∠EBC:∠NPE=2:6,请求出∠AQE的度数(结果用α,β表示).
一、填空题(本大题共5个小题,每小题4分,共20分)
19.(4分)若a+b=2,则代数式a2﹣b2+4b= .
20.(4分)一个不透明的箱子里装有红、白、黄三种颜色的小球共36个,它们除颜色外其他均相同,其中红色球有12个,黄色球的数量是白色球数量的2倍.当箱子中三种颜色的小球个数不变的情况下,要使箱子中摸出1个白色球的概率为,则应再往箱子中放入白色球 个.
21.(4分)已知关于x的多项式mx﹣n与2x2﹣3x+4的乘积结果中不含x的二次项,且常数项为﹣6,则m+n的值为 .
22.(4分)在综合实践活动中,数学兴趣小组对各边长度都是整数、最大边长为k的三角形的个数m进行了探究.发现:当k=1时,只有{1,1,1}一种情况,即m=1;当k=2时,有{1,2,2}和{2,2,2}两种情况,即m=2;当k=3时,有{1,3,3},{2,2,3},{2,3,3}和{3,3,3}四种情况,即m=4;….若k=6,则m的值为 ;若k=19,则m的值为 .
23.(4分)如图,已知四边形ABCD是长方形,以BD为直角边作等腰直角三角形BDM,且∠BDM=90°,BM交AD于点N,连接AM.若长方形ABCD的周长为14,,则△ABM的面积为 .
二、解答题(本大题共3个小题,共30分)
24.(8分)将一个边长为3a+b(b>a)的正方形进行分割,得到若干个边长为a的正方形(这类正方形记为甲型),若干个边长为b的正方形(这类正方形记为乙型),若干个邻边长为a和b的长方形(这类长方形记为丙型).
(1)若分割后,甲、乙、丙三种规格的图形都要有,且b不是a的整数倍,求分割后甲、乙、丙各类图形的个数,并画出分割示意图;
(2)若已知丙型长方形的周长为24m,面积为32m2,求分割后一个甲型正方形与一个乙型正方形的面积之和.
25.(10分)用充电器给某手机充电时,其屏幕的起始画面如图.
经测试,在用快速充电器为手机充电时,其电量E(单位:%)与充电时间t(单位:min)之间的关系如表格所示.
充电时间t(单位:min) 0 10 20 30 40 50 …
手机电量E(单位:%) 20 28 36 44 52 60 …
(1)请求出E与t之间的关系式;
(2)若电量充到76%,请求出充电时间;
(3)已知该手机正常使用时耗电量为每小时10%,在用快速充电器将其充满电后,正常使用t小时,接着再用普通充电器将其充满电,普通充电器充电平均速度为每小时15%,其“充电﹣耗电﹣充电”的时间恰好是5小时,求t的值.
26.(12分)如图1,在四边形ABCD中,BC=CD,连接AC,BD交于点O,G为OB上一点,连接CG,有CG=CO.
(1)求证:DO=BG;
(2)若∠AOD=60°,∠ACB+∠ADB=180°,求线段AO,CO,DO之间的等量关系式;
(3)如图2,在(2)的条件下,在CD上取一点E,在BC上取一点F,使CF=CE,且∠CBE+∠CAD=∠BAC,在BD上点取一点M,连接BE,FM,且∠BFM=∠DAB,试判断FM,BD的位置关系,并说明理由.
2023-2024学年四川省成都市双流区七年级(下)期末数学试卷
参考答案
一、选择题(每小题4分,共32分)每小题均有四个选项,其中只有一项符合题目要求.
1.(4分)加快建设体育强国,就是要弘扬中华体育精神.下列体育图标是轴对称图形的是( )
A. B.
C. D.
选:B.
2.(4分)下列计算正确的是( )
A.a2+a3=2a5 B.a2 a3=a6
C.(3a3)2=9a6 D.5a6÷a3=5a2
选:C.
3.(4分)某种细胞的直径为0.0000000627米,将0.0000000627用科学记数法表示为( )
A.6.27×10﹣8 B.62.7×10﹣8 C.6.27×10﹣9 D.62.7×10﹣9
选:A.
4.(4分)若在△ABC中,若∠A:∠B:∠C=2:3:5,则△ABC是( )
A.直角三角形 B.等腰三角形
C.锐角三角形 D.钝角三角形
选:A.
5.(4分)下列诗句表述的是随机事件的是( )
A.离离原上草,一岁一枯荣
B.危楼高百尺,手可摘星辰
C.会当凌绝顶,一览众山小
D.东边日出西边雨,道是无晴却有晴
选:D.
6.(4分)一个等腰三角形的两边长分别是3cm和7cm,则它的周长是( )cm.
A.17 B.13 C.14或17 D.13或17
选:A.
7.(4分)一把直尺和一个含30°,60°角的三角板如图所示摆放,直尺一边与三角板的两直角边分别交于F,A两点,另一边与三角板的两直角边分别交于D,E两点,且∠BAF=20°,那么∠CED的大小为( )
A.20° B.30° C.40° D.50°
选:C.
8.(4分)某链条每节长为3.7cm,每两节链条相连部分重叠的圆的直径为1.2cm,按照这种连接方式,x节链条总长度为y cm,则y与x的关系式是( )
A.y=3.7x B.y=2.5x
C.y=2.5x﹣1.2 D.y=2.5x+1.2
选:D.
二、填空题(本大题共5个小题,每小题4分,共20分)
9.(4分)计算:x2y (﹣xy)= ﹣x3y2 .
10.(4分)若一个角的补角是110°,则这个角的度数为 70° .
11.(4分)如图,在4×4的正方形网格飞镖游戏板中,每块小正方形除颜色外都相同,小正方形的顶点称为格点.假设飞镖击中游戏板的每一处是等可能的(击中边界或没有击中游戏板,则重投一次),任意投掷飞镖一次,飞镖击中阴影部分的概率是 .
12.(4分)如图1,已知长方形ABCD中,动点M沿长方形ABCD的边以B→C→D→A的路径匀速运动到A处停止,记△ABM的面积为y,动点M运动的路程为x,y与x的关系如图2所示,则图2中的m的值为 7.5 .
13.(4分)如图,在△ABC中,分别以点A,B为圆心,大于的长度为半径画弧,两弧相交于点P,Q,连直线PQ与AB交于点E,与AC交于点D,连接BD,若AC=16,BC=10,则△BCD的周长为 26 .
三、解答题(本大题共5个小题,共48分)
14.(12分)(1)计算:.
(2)先化简,再求值:(3a+b)(3a﹣b)+(2a﹣b)2﹣3a(a﹣b),其中.
【解答】解:(1)
=1﹣2+9+1
=9;
(2)(3a+b)(3a﹣b)+(2a﹣b)2﹣3a(a﹣b)
=9a2﹣b2+4a2﹣4ab+b2﹣3a2+3ab
=10a2﹣ab,
当时,原式=10×()2﹣×2=10×﹣=﹣=﹣.
15.(8分)如图是由边长为1的小正方形组成的6×5网格,每个小正方形的顶点叫作格点.已知点A,B,C都在格点上,仅用无刻度的直尺在网格中按要求画图,画图过程用虚线表示,画图结果用实线表示.
(1)在图1中,AC上找一点D,使AD=CD,并连接BD;
(2)在图2中,AC上找一点E,连接BE,使BE⊥AC.
【解答】解:(1)如图,点D即为所求;
(2)如图,点E即为所求.
16.(8分)某商场进行“6 18”促销活动,设计了如下两种摇奖方式:
方式一:有一枚均匀的正二十面体形状的骰子,其中的1个面标有“1”,2个面标有“2”,3个面标有“3”,4个面标有“4”,5个面标有“5”,其余的面标有“6”.将这个骰子掷出后,“6”朝上则获奖;
方式二:一个均匀的转盘被等分成12份,分别标有1至12这12个数字.转动转盘,当转盘停止后,指针指向的数字为6的倍数则获奖.
(1)若采用方式一,骰子掷出后,“4”朝上的概率为 ;
(2)选择哪种摇奖方式获奖机会更大?请说明理由.
【解答】解:(1)“4”朝上的概率是=;
故答案为:;
(2)选择摇奖方式一.
理由如下:
方式一:标有数字6的面有20﹣1﹣2﹣3﹣4﹣5=15面,
选择摇奖方式一获奖的概率为=,
方式一:数字为6的倍数的数由6,12共2个,
选择摇奖方式二获奖的概率为=,
因为>,
所以摇奖方式一获奖的机会大,选择摇奖方式一.
17.(10分)杆秤是我国传统的计重工具,其历史由来已久.如图,可以用秤砣到秤纽的水平距离得出秤盘上所放物体的重量.称重时,若记秤砣到秤纽的水平距离为x(厘米),秤盘所放物体重量为y(斤),其部分对应数据如表.
第1组 第2组 第3组 第4组 第5组 第6组
x(厘米) 1 3 4 6 11 12
y(斤) 0.75 1.25 1.50 2.25 3.25 3.50
(1)请判断哪一组数据是错误的?并说明理由;
(2)求当秤盘所放物体重量为5斤时秤砣到秤纽的水平距离.
【解答】解:(1)第4组数据是错误的.理由如下:
在图2中对6组数据描点.
可以发现,x=6,y=2.25即第4组数据是错误的.
(2)设x、y的函数关系式为y=kx+b.
将第1组和第2组数据分别代入,得,
解得,
∴x、y的函数关系式为y=0.25x+0.5.
当y=5时,有5=0.25x+0.5,解得x=18.
∴当秤盘所放物体重量为5斤时秤砣到秤纽的水平距离是18厘米.
18.(10分)如图,直线l1∥l2,点A,B在l1上,点C,D在l2上,连接AD,BC,AC,点M在BA的延长线上,连接CM,CM与AD交于点N.已知∠BMC=∠BCA.
(1)求证:∠BCA=∠DCN;
(2)若∠ANM=∠BAC,请判断AD,BC的位置关系,并说明理由;
(3)在(2)的条件下,连接BN,E为CD上一点,连BE与NC,AC分别交于点P,Q,且∠EBN=∠ABN.若∠ABN的度数为α,∠NCD的度数为β,∠EBC:∠NPE=2:6,请求出∠AQE的度数(结果用α,β表示).
【解答】(1)证明:∵l1∥l2,
∴∠BMC=∠DCN,
又∵∠BMC=∠BCA,
∴∠BCA=∠DCN;
(2)解:AD∥BC,理由如下:
∵∠BAC=∠BMC+∠ACM,
又∵∠BMC=∠BCA,
∴∠BAC=∠BCA+∠ACM=∠BCM,
∵∠ANM=∠BAC,
∴∠ANM=∠BCM,
∴AD∥BC;
(3)解:∵∠NCD的度数为β,
∴∠BCA=∠DCN=β=∠BMC,
∴∠AQE=∠BQC=180°﹣∠EBC﹣∠BCA=180°﹣∠EBC﹣β,
∵∠EBC:∠NPE=2:6,
∴∠EBC=∠NPE,
∵∠NPE=∠BMC+∠MBP=β+∠MBP,
∠MBP=∠ABN+∠EBN,
又∵∠EBN=∠ABN.∠ABN的度数为α,
∴∠MBP=α+α=2α,
∴∠NPE=β+∠MBP=β+2α,
∴∠EBC=(β+2α),
∴∠AQE=180°﹣(β+2α)﹣β=180°﹣α﹣β.
一、填空题(本大题共5个小题,每小题4分,共20分)
19.(4分)若a+b=2,则代数式a2﹣b2+4b= 4 .
【解答】解:∵a+b=2,
∴a2﹣b2+4b
=(a+b)(a﹣b)+4b
=2(a﹣b)+4b
=2a+2b=2(a+b)
=2×2
=4,
故答案为:4.
20.(4分)一个不透明的箱子里装有红、白、黄三种颜色的小球共36个,它们除颜色外其他均相同,其中红色球有12个,黄色球的数量是白色球数量的2倍.当箱子中三种颜色的小球个数不变的情况下,要使箱子中摸出1个白色球的概率为,则应再往箱子中放入白色球 6 个.
【解答】解:设箱子里装有m个白色球,
则12+m+2m=36,
解得m=8,
∴白色球有8个,
设再往箱子中放入白色球x个,
则,
解得x=6,
经检验,x=6是方程的解,
∴应再往箱子中放入白色球6个.
故答案为:6.
21.(4分)已知关于x的多项式mx﹣n与2x2﹣3x+4的乘积结果中不含x的二次项,且常数项为﹣6,则m+n的值为 .
【解答】解:(mx﹣n)(2x2﹣3x+4)=2mx3﹣(3m+2n)x2+(4m+3n)x﹣4n,
∵结果中不含x的二次项,且常数项为﹣6,
∴﹣4n=﹣6,3m+2n=0,
∴n=,m=﹣1,
∴m+n=﹣1+=.
故答案为:.
22.(4分)在综合实践活动中,数学兴趣小组对各边长度都是整数、最大边长为k的三角形的个数m进行了探究.发现:当k=1时,只有{1,1,1}一种情况,即m=1;当k=2时,有{1,2,2}和{2,2,2}两种情况,即m=2;当k=3时,有{1,3,3},{2,2,3},{2,3,3}和{3,3,3}四种情况,即m=4;….若k=6,则m的值为 12 ;若k=19,则m的值为 100 .
【解答】解:由题知,
当k=1时,m=1;
当k=2时,m=2;
当k=3时,m=4;
当k=4时,有如下情况:
{1,4,4},{2,3,4},{2,4,4},{3,3,4},{3,4,4},{4,4,4},
所以m=6,
以此类推,当k=5时,m=9;
当k=6时,m=12;
…,
因为1=1,
2=1+1,
4=1+2+1,
6=1+2+2+1,
9=1+2+3+2+1,
12=1+2+3+3+2+1,
…,
所以当k=19时,
m=1+2+3+4+5+6+7+8+9+10+9+8+7+6+5+4+3+2+1=100.
故答案为:12,100.
23.(4分)如图,已知四边形ABCD是长方形,以BD为直角边作等腰直角三角形BDM,且∠BDM=90°,BM交AD于点N,连接AM.若长方形ABCD的周长为14,,则△ABM的面积为 .
【解答】解:如图,过M作MG⊥CD交CD的延长线于点G,
∵△BDM为等腰直角三角形,
∴∠BDM=90°,DB=DM,
∴∠MDG=∠DBC=90°﹣∠BDC,
在△MGD和△DCB中,
,
∴△MGD≌△DCB(AAS),
∴DG=BC,
∵长方形ABCD的周长为14,
∴BC+CD=×14=7,
∴DG+CD=7,
∴S△ABM=S△ABN+S△ANM=AN AB+AN DG=AN (DG+AB)=××7=.
故答案为:.
二、解答题(本大题共3个小题,共30分)
24.(8分)将一个边长为3a+b(b>a)的正方形进行分割,得到若干个边长为a的正方形(这类正方形记为甲型),若干个边长为b的正方形(这类正方形记为乙型),若干个邻边长为a和b的长方形(这类长方形记为丙型).
(1)若分割后,甲、乙、丙三种规格的图形都要有,且b不是a的整数倍,求分割后甲、乙、丙各类图形的个数,并画出分割示意图;
(2)若已知丙型长方形的周长为24m,面积为32m2,求分割后一个甲型正方形与一个乙型正方形的面积之和.
【解答】解:(1)∵(3a+b)2=9a2+6ab+b2,
∴甲类图形有9个,乙类图形有1个,丙类图形有6个.
分割示意图如图所示,
(2)∵丙型长方形的周长为24m,面积为32m2,
∴a+b=12,ab=32,
a2+b2=(a+b)2﹣2ab=122﹣64=80(m2),
即分割后一个甲型正方形与一个乙型正方形的面积之和为80m2.
25.(10分)用充电器给某手机充电时,其屏幕的起始画面如图.
经测试,在用快速充电器为手机充电时,其电量E(单位:%)与充电时间t(单位:min)之间的关系如表格所示.
充电时间t(单位:min) 0 10 20 30 40 50 …
手机电量E(单位:%) 20 28 36 44 52 60 …
(1)请求出E与t之间的关系式;
(2)若电量充到76%,请求出充电时间;
(3)已知该手机正常使用时耗电量为每小时10%,在用快速充电器将其充满电后,正常使用t小时,接着再用普通充电器将其充满电,普通充电器充电平均速度为每小时15%,其“充电﹣耗电﹣充电”的时间恰好是5小时,求t的值.
【解答】解:(1)由题意得,根据表格数据函数图象过(0,20),(10,28),
设函数关系式为E=kt+b,
∴.
∴k=0.8,b=20.
∴E与t的关系式为E=0.8t+20.
(2)由题意,结合(1)E=0.8t+20,
令E=76,
∴0.8t+20=76.
∴t=70.
答:充电时间为70min.
(3)由题意得,令E=100,
∴快充充满电需要的时间为100min=h.
∴15(5﹣﹣t)=10t.
∴t=2.
26.(12分)如图1,在四边形ABCD中,BC=CD,连接AC,BD交于点O,G为OB上一点,连接CG,有CG=CO.
(1)求证:DO=BG;
(2)若∠AOD=60°,∠ACB+∠ADB=180°,求线段AO,CO,DO之间的等量关系式;
(3)如图2,在(2)的条件下,在CD上取一点E,在BC上取一点F,使CF=CE,且∠CBE+∠CAD=∠BAC,在BD上点取一点M,连接BE,FM,且∠BFM=∠DAB,试判断FM,BD的位置关系,并说明理由.
【解答】(1)证明:过C作CH⊥BD于点H,
∵CB=CD,CO=CG,
∴DH=BH,OH=GH,
∴DH﹣OH=BH﹣GH,
∴DO=BG;
(2)解:AO=DO+CO,证明如下,
方法一:在OA上取一点M,连接DM,使DM=DO,
∵∠AOD=60°,DM=DO,
∴△DOM为等边三角形,
∴DM=DO=OM,
∵CO=CG,∠COG=∠AOD=60°,
∴△COG为等边三角形,
∴∠OCG=60°,
∵∠DAO+∠AOD+∠ADB=180°,且∠ACB+∠ADB=180°,
∴∠DAO+∠AOD=∠ACB=∠OCG+∠BCG,
∵∠AOD=∠OCG=60°,
∴∠DAO=∠BCG,
由(1)中方法可得,∠DCH=∠BCH,∠OCH=∠GCH,
∴∠DCH﹣∠OCH=∠BCH﹣∠GCH,
即∠DCO=∠BCG,
∴∠DCO=∠DAO,
∵∠DMA=∠DOC=120°,
∴△DAM≌△DCO(AAS),
∴AM=OC,
∵AO=AM+OM,
∴AO=DO+CO.
方法二:如图,作DQ⊥AC于点Q,
由方法一得出DA=DC,
∴AQ=CQ,
设OQ=x,OC=y,则AQ=CQ=x+y,
∴AO=AQ+OQ=2x+y,
∵∠AOD=60°,
∴∠ODQ=30°,
∴OD﹣2OQ=2x,
∴OD+OC=2x+y=AO,
∴AO=DO+CO.
(3)解:FM⊥BD,理由如下,
如图,连接DF,
∵CB=CD,∠BCE=∠CDF,CE=CF,
∴△BCE≌△DCF(SAS),
∴∠BEC=∠DFC,∠CBE=∠CDF,
设∠ACB=α,∠BAC=β,
∵∠ACB+∠ADB=180°,
∴∠ADB=180°﹣α,
∵∠AOD=60°,
∴∠CAD=α﹣60°=∠DCA,
∴∠BCE=∠DCA+∠ACB=2α﹣60°,
∴∠CBD==120°﹣α,
∵∠CBE+∠CAD=∠BAC,
∴∠CBE=∠BAC﹣∠CAD=β﹣α+60°=∠CDF,
∵∠CEB=180°﹣∠CBE﹣∠BCE=180°﹣(β﹣α+60°)﹣(2α﹣60°)=180°﹣α﹣β,
∴∠CFD=180°﹣α﹣β,
∵∠BFM=∠DAB=∠DAC+∠BAC=α﹣60°+β,
∴∠DFM=180°﹣∠CFD﹣∠BFM=180°﹣(180°﹣α﹣β)﹣(α﹣60°+β)=60°,
由(2)得AO=DO+CO=OG+BG=OB,∠AOD=60°,
∴∠OBA=∠OAB=30°,即β=30°,
∵∠FDB=180°﹣∠CBD﹣∠BFD=180°﹣(120°﹣α)﹣(α+β)=60°﹣β=30°,
∴∠FMD=180°﹣∠FDM﹣∠DFM=90°,
∴FM⊥BD.
同课章节目录
