2023-2024学年山东省东营市东营区七年级(下)期末数学试卷(五四学制)(含答案)
文档属性
| 名称 | 2023-2024学年山东省东营市东营区七年级(下)期末数学试卷(五四学制)(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 515.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-30 19:59:18 | ||
图片预览




文档简介
2023-2024学年山东省东营市东营区七年级(下)期末数学试卷(五四学制)
一、选择题:本大题共10小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来,每小题选对得3分,选错、不选或选出的答案超过一个均记零分。
1.(3分)下列方程组中是二元一次方程组的是( )
A. B.
C. D.
2.(3分)若a>b,则下列不等式变形不正确的是( )
A.﹣2a<﹣2b B.am<bm C.a﹣1>b﹣1 D.+1>+1
3.(3分)下列命题中,是假命题的是( )
A.对顶角相等
B.等腰三角形的两底角相等
C.两直线平行,同旁内角互补
D.面积相等的两个三角形全等
4.(3分)将不等式组的解集表示在数轴上,正确的是( )
A.
B.
C.
D.
5.(3分)如图,在Rt△ABC中,∠A=60°,∠C=90°,点B在直线a上,直线a∥b,若∠1=108°,则∠2的度数为( )
A.38° B.42° C.48° D.52°
6.(3分)如图,在△ABC和△ADE中,已知AB=AD,还需要添加两个条件,才能使△ABC≌△ADE,不能添加的一组是( )
A.BC=DE,AC=AE B.∠B=∠D,∠BAC=∠DAE
C.BC=DE,∠C=∠E D.AC=AE,∠BAD=∠CAE
7.(3分)如图,在△ABC中,BF平分∠ABC,CF平分∠ACB,∠BFC=125°,则∠A的度数为( )
A.60° B.80° C.70° D.45°
8.(3分)如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和38,则△EDF的面积为( )
A.8 B.12 C.4 D.6
9.(3分)我国明代《算法统宗》一书中有这样一题:“一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托(一托按照5尺计算).”大意是:现有一根竿和一条绳索,如果用绳索去量竿,绳索比竿长5尺;如果将绳索对折后再去量竿,就比竿短5尺,则绳索长几尺?设竿长x尺,绳索长y尺,根据题意可列方程组为( )
A. B.
C. D.
10.(3分)如图,已知AD是△ABC的角平分线,AD的中垂线交AB于点F,交BC的延长线于点E.以下四个结论:①∠EAD=∠EDA;②DF∥AC;③∠FDE=90°;④∠B=∠CAE.恒成立的结论有( )
A.①② B.②③④ C.①②④ D.①②③④
二、填空题:本大题共8小题,其中11-14题每小题3分,15-18题每小题3分,共28分。只要求填写最后结果。
11.(3分)暑假将至,东营区教育局向全区师生发出倡议“不去河沟游玩,防落水,不去河沟游泳,防溺水”.在这句宣传语中,“水”字出现的频率为 .
12.(3分)已知是关于x,y的二元一次方程mx+3y=1的一个解,则m的值为 .
13.(3分)某大学举办“学习强国”知识竞赛,规定答对一题得20分,答错一题扣10分,在8道必答题中,得分不低于100分即可进入下一轮,冉冉进入了下一轮,则冉冉答错题数最多为 .
14.(3分)如图,在△ABC中,∠C=90°,AB的垂直平分线交AB于点D,交BC于点E,连接AE,若CE=5,AC=12,则BE的长是 .
15.(4分)若关于x的一元一次不等式组无解,则a的取值范围为 .
16.(4分)腰长为4a,底角为15°的等腰三角形的面积为 .
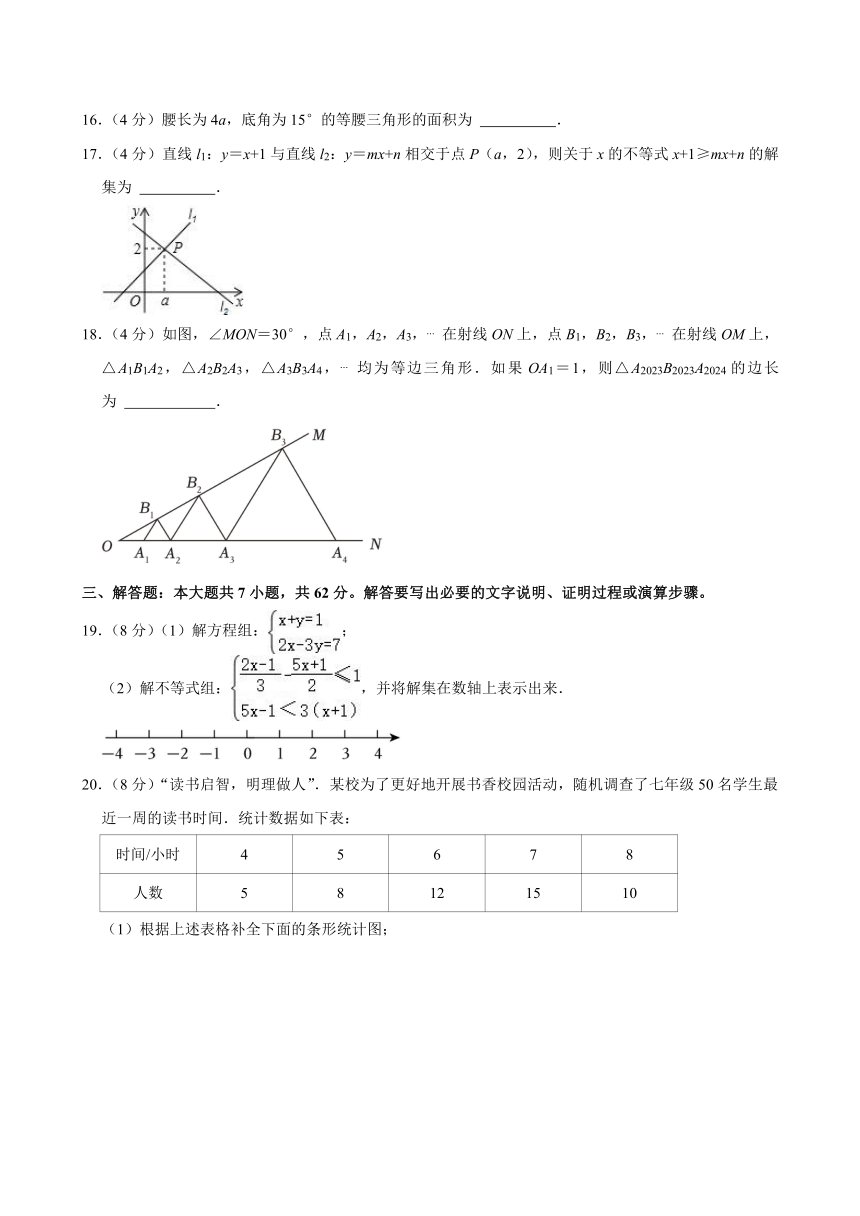
17.(4分)直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2),则关于x的不等式x+1≥mx+n的解集为 .
18.(4分)如图,∠MON=30°,点A1,A2,A3, 在射线ON上,点B1,B2,B3, 在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4, 均为等边三角形.如果OA1=1,则△A2023B2023A2024的边长为 .
三、解答题:本大题共7小题,共62分。解答要写出必要的文字说明、证明过程或演算步骤。
19.(8分)(1)解方程组:;
(2)解不等式组:,并将解集在数轴上表示出来.
20.(8分)“读书启智,明理做人”.某校为了更好地开展书香校园活动,随机调查了七年级50名学生最近一周的读书时间.统计数据如下表:
时间/小时 4 5 6 7 8
人数 5 8 12 15 10
(1)根据上述表格补全下面的条形统计图;
(2)若该校七年级有600名学生.则近一周的读书时间为6小时的大约有多少名学生;
(3)学校欲从这50名学生中,随机抽取1名学生参加上级部门组织的读书活动,其中被抽到学生的读书时间不少于7小时的概率是多少?
21.(8分)如图,在△ABC中,已知点D在线段AB的反向延长线上,过AC的中点F作线段GE交∠DAC的平分线于E,交BC于G,且AE∥BC.
(1)求证:△ABC是等腰三角形;
(2)若AE=8,AB=10,GC=2BG,求△ABC的周长.
22.(8分)一个不透明的袋中装有红、黄、白三种颜色的球共40个,它们除颜色外都相同,其中白球比红球的2倍多1个,已知从袋中摸出一个球是黄球的概率是.
(1)求袋中黄球的个数;
(2)求从袋中摸出一个球是红球的概率;
(3)现向袋中放入m个白球,同时拿出红球和黄球共m个,若从袋中摸出一个球是白球的概率为,求m的值.
23.(8分)完成下面的证明:
如图,已知∠A=∠F,∠C=∠D,求证:BD∥CE.
24.(10分)我市在创建全国文明城市过程中,决定购买A,B两种树苗对某路段道路进行绿化改造,已知购买A种树苗8棵,B种树苗3棵,要950元;若购买A种树苗5棵,B种树苗6棵,则需要800元.
(1)求购买A,B两种树苗每棵各需多少元?
(2)考虑到绿化效果和资金周转,购进A种树苗要多于B种树苗,且用于购买这两种树苗的总资金不能超过7650元,若购进这两种树苗共100棵,则有哪几种购买方案?哪种购买方案最省钱?
25.(12分)(感知)如图1所示,△ABC是等边三角形,D是边BC上一点(点D不与点B,C重合),作∠EDF=60°,使角的两边分别交边AB,AC于点E,F,且BD=CF.若DE⊥BC,则∠DFC的大小是 .
(探究)如图2所示,△ABC是等边三角形,D是边BC上一点(点D不与点B,C重合),作∠EDF=60°,使角的两边分别交边AB,AC于点E,F,且BD=CF.求证:BE=CD.
(应用)如图3所示,△ABC是等边三角形,若D是边BC的中点,且AB=2,∠EDF=60°,且BD=CF.求四边形AEDF的周长.
2023-2024学年山东省东营市东营区七年级(下)期末数学试卷(五四学制)
参考答案
一、选择题:本大题共10小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来,每小题选对得3分,选错、不选或选出的答案超过一个均记零分。
1.(3分)下列方程组中是二元一次方程组的是( )
A. B.
C. D.
选:C.
2.(3分)若a>b,则下列不等式变形不正确的是( )
A.﹣2a<﹣2b B.am<bm C.a﹣1>b﹣1 D.+1>+1
选:B.
3.(3分)下列命题中,是假命题的是( )
A.对顶角相等
B.等腰三角形的两底角相等
C.两直线平行,同旁内角互补
D.面积相等的两个三角形全等
选:D.
4.(3分)将不等式组的解集表示在数轴上,正确的是( )
A.
B.
C.
D.
选:C.
5.(3分)如图,在Rt△ABC中,∠A=60°,∠C=90°,点B在直线a上,直线a∥b,若∠1=108°,则∠2的度数为( )
A.38° B.42° C.48° D.52°
选:B.
6.(3分)如图,在△ABC和△ADE中,已知AB=AD,还需要添加两个条件,才能使△ABC≌△ADE,不能添加的一组是( )
A.BC=DE,AC=AE B.∠B=∠D,∠BAC=∠DAE
C.BC=DE,∠C=∠E D.AC=AE,∠BAD=∠CAE
选:C.
7.(3分)如图,在△ABC中,BF平分∠ABC,CF平分∠ACB,∠BFC=125°,则∠A的度数为( )
A.60° B.80° C.70° D.45°
选:C.
8.(3分)如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和38,则△EDF的面积为( )
A.8 B.12 C.4 D.6
选:D.
9.(3分)我国明代《算法统宗》一书中有这样一题:“一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托(一托按照5尺计算).”大意是:现有一根竿和一条绳索,如果用绳索去量竿,绳索比竿长5尺;如果将绳索对折后再去量竿,就比竿短5尺,则绳索长几尺?设竿长x尺,绳索长y尺,根据题意可列方程组为( )
A. B.
C. D.
选:A.
10.(3分)如图,已知AD是△ABC的角平分线,AD的中垂线交AB于点F,交BC的延长线于点E.以下四个结论:①∠EAD=∠EDA;②DF∥AC;③∠FDE=90°;④∠B=∠CAE.恒成立的结论有( )
A.①② B.②③④ C.①②④ D.①②③④
选:C.
二、填空题:本大题共8小题,其中11-14题每小题3分,15-18题每小题3分,共28分。只要求填写最后结果。
11.(3分)暑假将至,东营区教育局向全区师生发出倡议“不去河沟游玩,防落水,不去河沟游泳,防溺水”.在这句宣传语中,“水”字出现的频率为 .
12.(3分)已知是关于x,y的二元一次方程mx+3y=1的一个解,则m的值为 5 .
13.(3分)某大学举办“学习强国”知识竞赛,规定答对一题得20分,答错一题扣10分,在8道必答题中,得分不低于100分即可进入下一轮,冉冉进入了下一轮,则冉冉答错题数最多为 2道 .
14.(3分)如图,在△ABC中,∠C=90°,AB的垂直平分线交AB于点D,交BC于点E,连接AE,若CE=5,AC=12,则BE的长是 13 .
15.(4分)若关于x的一元一次不等式组无解,则a的取值范围为 a≤﹣2 .
16.(4分)腰长为4a,底角为15°的等腰三角形的面积为 4a2 .
17.(4分)直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2),则关于x的不等式x+1≥mx+n的解集为 x≥1 .
18.(4分)如图,∠MON=30°,点A1,A2,A3, 在射线ON上,点B1,B2,B3, 在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4, 均为等边三角形.如果OA1=1,则△A2023B2023A2024的边长为 22022 .
三、解答题:本大题共7小题,共62分。解答要写出必要的文字说明、证明过程或演算步骤。
19.(8分)(1)解方程组:;
(2)解不等式组:,并将解集在数轴上表示出来.
【解答】解:(1),
①×3+②得,5x=10,
∴x=2,
把x=2代入①得,2+y=1,
∴y=﹣1,
∴方程组的解为;
(2),
由①得,x≥﹣1,
由②得,x<2,
∴不等式组的解集为﹣1≤x<2,
不等式组的解集在数轴上表示为:
20.(8分)“读书启智,明理做人”.某校为了更好地开展书香校园活动,随机调查了七年级50名学生最近一周的读书时间.统计数据如下表:
时间/小时 4 5 6 7 8
人数 5 8 12 15 10
(1)根据上述表格补全下面的条形统计图;
(2)若该校七年级有600名学生.则近一周的读书时间为6小时的大约有多少名学生;
(3)学校欲从这50名学生中,随机抽取1名学生参加上级部门组织的读书活动,其中被抽到学生的读书时间不少于7小时的概率是多少?
【解答】解:(1)补全统计图如图,
(2)(人);
(3)从这50名学生中,随机抽取1名学生参加上级部门组织的读书活动,其中被抽到学生的读书时间不少于7小时的概率.
21.(8分)如图,在△ABC中,已知点D在线段AB的反向延长线上,过AC的中点F作线段GE交∠DAC的平分线于E,交BC于G,且AE∥BC.
(1)求证:△ABC是等腰三角形;
(2)若AE=8,AB=10,GC=2BG,求△ABC的周长.
【解答】证明:(1)∵AE∥BC,
∴∠B=∠DAE,∠C=∠CAE.
∵AE平分∠DAC,
∴∠DAE=∠CAE.
∴∠B=∠C.
∴AB=AC.
∴△ABC是等腰三角形.
(2)∵F是AC的中点,
∴AF=CF.
∵AE∥BC,
∴∠C=∠CAE.
由对顶角相等可知:∠AFE=∠GFC.
在△AFE和△CFG中,
∴△AFE≌△CFG.
∴AE=GC=8.
∵GC=2BG,
∴BG=4.
∴BC=12.
∴△ABC的周长=AB+AC+BC=10+10+12=32.
22.(8分)一个不透明的袋中装有红、黄、白三种颜色的球共40个,它们除颜色外都相同,其中白球比红球的2倍多1个,已知从袋中摸出一个球是黄球的概率是.
(1)求袋中黄球的个数;
(2)求从袋中摸出一个球是红球的概率;
(3)现向袋中放入m个白球,同时拿出红球和黄球共m个,若从袋中摸出一个球是白球的概率为,求m的值.
【解答】解:(1)根据题意得:
40×=24(个).
答:袋中黄球有24个;
(2)设红球有x个,则白球有(2x+1)个,
根据题意得x+2x+1=40﹣24,
解得x=5.
所以从袋中摸出一个球是红球的概率为=;
(3)∵向袋中放入m个白球,同时拿出红球和黄球共m个,
∴球的总数没有变化,白球共有2×5+1+m=11+m(个).
根据题意得,=,
解得,m=5.
23.(8分)完成下面的证明:
如图,已知∠A=∠F,∠C=∠D,求证:BD∥CE.
【解答】证明:∵∠A=∠F,
∴AC∥DF,
∴∠ABD=∠D,
∵∠C=∠D,
∴∠ABD=∠C,
∴BD∥CE.
24.(10分)我市在创建全国文明城市过程中,决定购买A,B两种树苗对某路段道路进行绿化改造,已知购买A种树苗8棵,B种树苗3棵,要950元;若购买A种树苗5棵,B种树苗6棵,则需要800元.
(1)求购买A,B两种树苗每棵各需多少元?
(2)考虑到绿化效果和资金周转,购进A种树苗要多于B种树苗,且用于购买这两种树苗的总资金不能超过7650元,若购进这两种树苗共100棵,则有哪几种购买方案?哪种购买方案最省钱?
【解答】解:(1)设购买A种树苗每棵需x元,B种树苗每棵需y元,
依题意得,
解得.
答:购买A种树苗每棵需100元,B种树苗每棵需50元.
(2)设购进A种树苗m棵,则购进B种树苗(100﹣m)棵,
依题意得:,
解得:50<m≤53,
又∵m为正整数,
∴m可以为51,52,53,
∴共有3种购买方案,
方案1:购进A种树苗51棵,B种树苗49棵;51×100+49×50=7550元,
方案2:购进A种树苗52棵,B种树苗48棵;52×100+48×50=7600元,
方案3:购进A种树苗53棵,B种树苗47棵.53×100+47×50=7650元,
∴购进A种树苗51棵,B种树苗49棵最省钱.
25.(12分)(感知)如图1所示,△ABC是等边三角形,D是边BC上一点(点D不与点B,C重合),作∠EDF=60°,使角的两边分别交边AB,AC于点E,F,且BD=CF.若DE⊥BC,则∠DFC的大小是 90° .
(探究)如图2所示,△ABC是等边三角形,D是边BC上一点(点D不与点B,C重合),作∠EDF=60°,使角的两边分别交边AB,AC于点E,F,且BD=CF.求证:BE=CD.
(应用)如图3所示,△ABC是等边三角形,若D是边BC的中点,且AB=2,∠EDF=60°,且BD=CF.求四边形AEDF的周长.
【解答】(感知)解:如图1,
∵△ABC是等边三角形,
∴∠C=60°,
∵DE⊥BC,
∴∠EDC=90°,
∵∠EDF=60°,
∴∠FDC=EDC﹣∠EDF=90°﹣60°=30°,
∴∠DFC=180°﹣∠FDC﹣∠C=180°﹣30°﹣60=90°,
故答案为:90°;
(探究)证明:如图2,
∵△ABC是等边三角形,
∴∠B=∠C=60°,
∵∠EDF=60°,
∴∠B=∠EDF,
∵∠EDC是△BED的外角,
∴∠B+∠BED=∠EDF+∠CDF,
∴∠BED=∠CDF,
在△BED和△CDF中,
,
∴△BED≌△CDF(AAS),
∴BE=CD;
(应用)解:如图3,
∵△ABC是等边三角形,AB=2,
∴∠B=∠C=60°,AB=BC=CA=2,
∵D是BC的中点,BD=CF,
∴BD=CD=CF=AF=1,
由探究可知△DBE≌△FCD,
∴BE=CD=1,DE=DF,
∵∠B=60°,
∴△BDE是等边三角形,
∴DF=DE=BD=1,
∴四边形AEDF的周长=AE+DE+DF+AF=4.
一、选择题:本大题共10小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来,每小题选对得3分,选错、不选或选出的答案超过一个均记零分。
1.(3分)下列方程组中是二元一次方程组的是( )
A. B.
C. D.
2.(3分)若a>b,则下列不等式变形不正确的是( )
A.﹣2a<﹣2b B.am<bm C.a﹣1>b﹣1 D.+1>+1
3.(3分)下列命题中,是假命题的是( )
A.对顶角相等
B.等腰三角形的两底角相等
C.两直线平行,同旁内角互补
D.面积相等的两个三角形全等
4.(3分)将不等式组的解集表示在数轴上,正确的是( )
A.
B.
C.
D.
5.(3分)如图,在Rt△ABC中,∠A=60°,∠C=90°,点B在直线a上,直线a∥b,若∠1=108°,则∠2的度数为( )
A.38° B.42° C.48° D.52°
6.(3分)如图,在△ABC和△ADE中,已知AB=AD,还需要添加两个条件,才能使△ABC≌△ADE,不能添加的一组是( )
A.BC=DE,AC=AE B.∠B=∠D,∠BAC=∠DAE
C.BC=DE,∠C=∠E D.AC=AE,∠BAD=∠CAE
7.(3分)如图,在△ABC中,BF平分∠ABC,CF平分∠ACB,∠BFC=125°,则∠A的度数为( )
A.60° B.80° C.70° D.45°
8.(3分)如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和38,则△EDF的面积为( )
A.8 B.12 C.4 D.6
9.(3分)我国明代《算法统宗》一书中有这样一题:“一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托(一托按照5尺计算).”大意是:现有一根竿和一条绳索,如果用绳索去量竿,绳索比竿长5尺;如果将绳索对折后再去量竿,就比竿短5尺,则绳索长几尺?设竿长x尺,绳索长y尺,根据题意可列方程组为( )
A. B.
C. D.
10.(3分)如图,已知AD是△ABC的角平分线,AD的中垂线交AB于点F,交BC的延长线于点E.以下四个结论:①∠EAD=∠EDA;②DF∥AC;③∠FDE=90°;④∠B=∠CAE.恒成立的结论有( )
A.①② B.②③④ C.①②④ D.①②③④
二、填空题:本大题共8小题,其中11-14题每小题3分,15-18题每小题3分,共28分。只要求填写最后结果。
11.(3分)暑假将至,东营区教育局向全区师生发出倡议“不去河沟游玩,防落水,不去河沟游泳,防溺水”.在这句宣传语中,“水”字出现的频率为 .
12.(3分)已知是关于x,y的二元一次方程mx+3y=1的一个解,则m的值为 .
13.(3分)某大学举办“学习强国”知识竞赛,规定答对一题得20分,答错一题扣10分,在8道必答题中,得分不低于100分即可进入下一轮,冉冉进入了下一轮,则冉冉答错题数最多为 .
14.(3分)如图,在△ABC中,∠C=90°,AB的垂直平分线交AB于点D,交BC于点E,连接AE,若CE=5,AC=12,则BE的长是 .
15.(4分)若关于x的一元一次不等式组无解,则a的取值范围为 .
16.(4分)腰长为4a,底角为15°的等腰三角形的面积为 .
17.(4分)直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2),则关于x的不等式x+1≥mx+n的解集为 .
18.(4分)如图,∠MON=30°,点A1,A2,A3, 在射线ON上,点B1,B2,B3, 在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4, 均为等边三角形.如果OA1=1,则△A2023B2023A2024的边长为 .
三、解答题:本大题共7小题,共62分。解答要写出必要的文字说明、证明过程或演算步骤。
19.(8分)(1)解方程组:;
(2)解不等式组:,并将解集在数轴上表示出来.
20.(8分)“读书启智,明理做人”.某校为了更好地开展书香校园活动,随机调查了七年级50名学生最近一周的读书时间.统计数据如下表:
时间/小时 4 5 6 7 8
人数 5 8 12 15 10
(1)根据上述表格补全下面的条形统计图;
(2)若该校七年级有600名学生.则近一周的读书时间为6小时的大约有多少名学生;
(3)学校欲从这50名学生中,随机抽取1名学生参加上级部门组织的读书活动,其中被抽到学生的读书时间不少于7小时的概率是多少?
21.(8分)如图,在△ABC中,已知点D在线段AB的反向延长线上,过AC的中点F作线段GE交∠DAC的平分线于E,交BC于G,且AE∥BC.
(1)求证:△ABC是等腰三角形;
(2)若AE=8,AB=10,GC=2BG,求△ABC的周长.
22.(8分)一个不透明的袋中装有红、黄、白三种颜色的球共40个,它们除颜色外都相同,其中白球比红球的2倍多1个,已知从袋中摸出一个球是黄球的概率是.
(1)求袋中黄球的个数;
(2)求从袋中摸出一个球是红球的概率;
(3)现向袋中放入m个白球,同时拿出红球和黄球共m个,若从袋中摸出一个球是白球的概率为,求m的值.
23.(8分)完成下面的证明:
如图,已知∠A=∠F,∠C=∠D,求证:BD∥CE.
24.(10分)我市在创建全国文明城市过程中,决定购买A,B两种树苗对某路段道路进行绿化改造,已知购买A种树苗8棵,B种树苗3棵,要950元;若购买A种树苗5棵,B种树苗6棵,则需要800元.
(1)求购买A,B两种树苗每棵各需多少元?
(2)考虑到绿化效果和资金周转,购进A种树苗要多于B种树苗,且用于购买这两种树苗的总资金不能超过7650元,若购进这两种树苗共100棵,则有哪几种购买方案?哪种购买方案最省钱?
25.(12分)(感知)如图1所示,△ABC是等边三角形,D是边BC上一点(点D不与点B,C重合),作∠EDF=60°,使角的两边分别交边AB,AC于点E,F,且BD=CF.若DE⊥BC,则∠DFC的大小是 .
(探究)如图2所示,△ABC是等边三角形,D是边BC上一点(点D不与点B,C重合),作∠EDF=60°,使角的两边分别交边AB,AC于点E,F,且BD=CF.求证:BE=CD.
(应用)如图3所示,△ABC是等边三角形,若D是边BC的中点,且AB=2,∠EDF=60°,且BD=CF.求四边形AEDF的周长.
2023-2024学年山东省东营市东营区七年级(下)期末数学试卷(五四学制)
参考答案
一、选择题:本大题共10小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来,每小题选对得3分,选错、不选或选出的答案超过一个均记零分。
1.(3分)下列方程组中是二元一次方程组的是( )
A. B.
C. D.
选:C.
2.(3分)若a>b,则下列不等式变形不正确的是( )
A.﹣2a<﹣2b B.am<bm C.a﹣1>b﹣1 D.+1>+1
选:B.
3.(3分)下列命题中,是假命题的是( )
A.对顶角相等
B.等腰三角形的两底角相等
C.两直线平行,同旁内角互补
D.面积相等的两个三角形全等
选:D.
4.(3分)将不等式组的解集表示在数轴上,正确的是( )
A.
B.
C.
D.
选:C.
5.(3分)如图,在Rt△ABC中,∠A=60°,∠C=90°,点B在直线a上,直线a∥b,若∠1=108°,则∠2的度数为( )
A.38° B.42° C.48° D.52°
选:B.
6.(3分)如图,在△ABC和△ADE中,已知AB=AD,还需要添加两个条件,才能使△ABC≌△ADE,不能添加的一组是( )
A.BC=DE,AC=AE B.∠B=∠D,∠BAC=∠DAE
C.BC=DE,∠C=∠E D.AC=AE,∠BAD=∠CAE
选:C.
7.(3分)如图,在△ABC中,BF平分∠ABC,CF平分∠ACB,∠BFC=125°,则∠A的度数为( )
A.60° B.80° C.70° D.45°
选:C.
8.(3分)如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和38,则△EDF的面积为( )
A.8 B.12 C.4 D.6
选:D.
9.(3分)我国明代《算法统宗》一书中有这样一题:“一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托(一托按照5尺计算).”大意是:现有一根竿和一条绳索,如果用绳索去量竿,绳索比竿长5尺;如果将绳索对折后再去量竿,就比竿短5尺,则绳索长几尺?设竿长x尺,绳索长y尺,根据题意可列方程组为( )
A. B.
C. D.
选:A.
10.(3分)如图,已知AD是△ABC的角平分线,AD的中垂线交AB于点F,交BC的延长线于点E.以下四个结论:①∠EAD=∠EDA;②DF∥AC;③∠FDE=90°;④∠B=∠CAE.恒成立的结论有( )
A.①② B.②③④ C.①②④ D.①②③④
选:C.
二、填空题:本大题共8小题,其中11-14题每小题3分,15-18题每小题3分,共28分。只要求填写最后结果。
11.(3分)暑假将至,东营区教育局向全区师生发出倡议“不去河沟游玩,防落水,不去河沟游泳,防溺水”.在这句宣传语中,“水”字出现的频率为 .
12.(3分)已知是关于x,y的二元一次方程mx+3y=1的一个解,则m的值为 5 .
13.(3分)某大学举办“学习强国”知识竞赛,规定答对一题得20分,答错一题扣10分,在8道必答题中,得分不低于100分即可进入下一轮,冉冉进入了下一轮,则冉冉答错题数最多为 2道 .
14.(3分)如图,在△ABC中,∠C=90°,AB的垂直平分线交AB于点D,交BC于点E,连接AE,若CE=5,AC=12,则BE的长是 13 .
15.(4分)若关于x的一元一次不等式组无解,则a的取值范围为 a≤﹣2 .
16.(4分)腰长为4a,底角为15°的等腰三角形的面积为 4a2 .
17.(4分)直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2),则关于x的不等式x+1≥mx+n的解集为 x≥1 .
18.(4分)如图,∠MON=30°,点A1,A2,A3, 在射线ON上,点B1,B2,B3, 在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4, 均为等边三角形.如果OA1=1,则△A2023B2023A2024的边长为 22022 .
三、解答题:本大题共7小题,共62分。解答要写出必要的文字说明、证明过程或演算步骤。
19.(8分)(1)解方程组:;
(2)解不等式组:,并将解集在数轴上表示出来.
【解答】解:(1),
①×3+②得,5x=10,
∴x=2,
把x=2代入①得,2+y=1,
∴y=﹣1,
∴方程组的解为;
(2),
由①得,x≥﹣1,
由②得,x<2,
∴不等式组的解集为﹣1≤x<2,
不等式组的解集在数轴上表示为:
20.(8分)“读书启智,明理做人”.某校为了更好地开展书香校园活动,随机调查了七年级50名学生最近一周的读书时间.统计数据如下表:
时间/小时 4 5 6 7 8
人数 5 8 12 15 10
(1)根据上述表格补全下面的条形统计图;
(2)若该校七年级有600名学生.则近一周的读书时间为6小时的大约有多少名学生;
(3)学校欲从这50名学生中,随机抽取1名学生参加上级部门组织的读书活动,其中被抽到学生的读书时间不少于7小时的概率是多少?
【解答】解:(1)补全统计图如图,
(2)(人);
(3)从这50名学生中,随机抽取1名学生参加上级部门组织的读书活动,其中被抽到学生的读书时间不少于7小时的概率.
21.(8分)如图,在△ABC中,已知点D在线段AB的反向延长线上,过AC的中点F作线段GE交∠DAC的平分线于E,交BC于G,且AE∥BC.
(1)求证:△ABC是等腰三角形;
(2)若AE=8,AB=10,GC=2BG,求△ABC的周长.
【解答】证明:(1)∵AE∥BC,
∴∠B=∠DAE,∠C=∠CAE.
∵AE平分∠DAC,
∴∠DAE=∠CAE.
∴∠B=∠C.
∴AB=AC.
∴△ABC是等腰三角形.
(2)∵F是AC的中点,
∴AF=CF.
∵AE∥BC,
∴∠C=∠CAE.
由对顶角相等可知:∠AFE=∠GFC.
在△AFE和△CFG中,
∴△AFE≌△CFG.
∴AE=GC=8.
∵GC=2BG,
∴BG=4.
∴BC=12.
∴△ABC的周长=AB+AC+BC=10+10+12=32.
22.(8分)一个不透明的袋中装有红、黄、白三种颜色的球共40个,它们除颜色外都相同,其中白球比红球的2倍多1个,已知从袋中摸出一个球是黄球的概率是.
(1)求袋中黄球的个数;
(2)求从袋中摸出一个球是红球的概率;
(3)现向袋中放入m个白球,同时拿出红球和黄球共m个,若从袋中摸出一个球是白球的概率为,求m的值.
【解答】解:(1)根据题意得:
40×=24(个).
答:袋中黄球有24个;
(2)设红球有x个,则白球有(2x+1)个,
根据题意得x+2x+1=40﹣24,
解得x=5.
所以从袋中摸出一个球是红球的概率为=;
(3)∵向袋中放入m个白球,同时拿出红球和黄球共m个,
∴球的总数没有变化,白球共有2×5+1+m=11+m(个).
根据题意得,=,
解得,m=5.
23.(8分)完成下面的证明:
如图,已知∠A=∠F,∠C=∠D,求证:BD∥CE.
【解答】证明:∵∠A=∠F,
∴AC∥DF,
∴∠ABD=∠D,
∵∠C=∠D,
∴∠ABD=∠C,
∴BD∥CE.
24.(10分)我市在创建全国文明城市过程中,决定购买A,B两种树苗对某路段道路进行绿化改造,已知购买A种树苗8棵,B种树苗3棵,要950元;若购买A种树苗5棵,B种树苗6棵,则需要800元.
(1)求购买A,B两种树苗每棵各需多少元?
(2)考虑到绿化效果和资金周转,购进A种树苗要多于B种树苗,且用于购买这两种树苗的总资金不能超过7650元,若购进这两种树苗共100棵,则有哪几种购买方案?哪种购买方案最省钱?
【解答】解:(1)设购买A种树苗每棵需x元,B种树苗每棵需y元,
依题意得,
解得.
答:购买A种树苗每棵需100元,B种树苗每棵需50元.
(2)设购进A种树苗m棵,则购进B种树苗(100﹣m)棵,
依题意得:,
解得:50<m≤53,
又∵m为正整数,
∴m可以为51,52,53,
∴共有3种购买方案,
方案1:购进A种树苗51棵,B种树苗49棵;51×100+49×50=7550元,
方案2:购进A种树苗52棵,B种树苗48棵;52×100+48×50=7600元,
方案3:购进A种树苗53棵,B种树苗47棵.53×100+47×50=7650元,
∴购进A种树苗51棵,B种树苗49棵最省钱.
25.(12分)(感知)如图1所示,△ABC是等边三角形,D是边BC上一点(点D不与点B,C重合),作∠EDF=60°,使角的两边分别交边AB,AC于点E,F,且BD=CF.若DE⊥BC,则∠DFC的大小是 90° .
(探究)如图2所示,△ABC是等边三角形,D是边BC上一点(点D不与点B,C重合),作∠EDF=60°,使角的两边分别交边AB,AC于点E,F,且BD=CF.求证:BE=CD.
(应用)如图3所示,△ABC是等边三角形,若D是边BC的中点,且AB=2,∠EDF=60°,且BD=CF.求四边形AEDF的周长.
【解答】(感知)解:如图1,
∵△ABC是等边三角形,
∴∠C=60°,
∵DE⊥BC,
∴∠EDC=90°,
∵∠EDF=60°,
∴∠FDC=EDC﹣∠EDF=90°﹣60°=30°,
∴∠DFC=180°﹣∠FDC﹣∠C=180°﹣30°﹣60=90°,
故答案为:90°;
(探究)证明:如图2,
∵△ABC是等边三角形,
∴∠B=∠C=60°,
∵∠EDF=60°,
∴∠B=∠EDF,
∵∠EDC是△BED的外角,
∴∠B+∠BED=∠EDF+∠CDF,
∴∠BED=∠CDF,
在△BED和△CDF中,
,
∴△BED≌△CDF(AAS),
∴BE=CD;
(应用)解:如图3,
∵△ABC是等边三角形,AB=2,
∴∠B=∠C=60°,AB=BC=CA=2,
∵D是BC的中点,BD=CF,
∴BD=CD=CF=AF=1,
由探究可知△DBE≌△FCD,
∴BE=CD=1,DE=DF,
∵∠B=60°,
∴△BDE是等边三角形,
∴DF=DE=BD=1,
∴四边形AEDF的周长=AE+DE+DF+AF=4.
同课章节目录
