2021-2022学年广东省湛江市吴川市广大实验学校八年级(下)期末数学试卷(含答案)
文档属性
| 名称 | 2021-2022学年广东省湛江市吴川市广大实验学校八年级(下)期末数学试卷(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 331.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-30 17:55:03 | ||
图片预览



文档简介
2021-2022学年广东省湛江市吴川市广大实验学校八年级(下)期末数学试卷
一.选择题(共10小题,每小题3分,共30分)
1.(3分)如果有意义,那么x的取值范围是( )
A.x>1 B.x≥1 C.x≤1 D.x<1
2.(3分)下列计算正确的是( )
A. B. C.3+2=5 D.=2
3.(3分)下列各组数中,能构成直角三角形的是( )
A.4,5,6 B.6,8,11 C.1,1, D.5,12,10
4.(3分)若函数y=x+k﹣2是正比例函数,则k的值是( )
A.6 B.4 C.2 D.﹣2
5.(3分)如图,在平行四边形ABCD中,AE平分∠BAD,交CD边于E,AD=3,AB=5,则EC的长为( )
A.1 B.2 C.3 D.5
6.(3分)如图,在矩形ABCD中,∠BOC=120°,AC=4,则AB的长为( )
A.2 B.4 C.2 D.4
7.(3分)秦始皇兵马俑博物馆拟招聘一名优秀讲解员,张力的笔试、试讲、面试三轮测试成绩分别为90分、94分、92分.综合成绩中笔试占50%、试讲占30%、面试占20%,那么张力的最后得分为( )
A.91分 B.91.6分 C.92分 D.93分
8.(3分)如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=3,AF=5,则AC的长为( )
A.4 B.4 C.10 D.8
9.(3分)对于函数y=﹣2x﹣1,下列结论正确的是( )
A.它的图象必经过点(﹣1,0)
B.它的图象经过第一、二、三象限
C.当x>1时,y<0
D.y的值随x值的增大而增大
10.(3分)如图,已知正比例函数与一次函数的图象交于点P,则以下结论:
①a>0;②2a+b=1;③当x<0时,y1>0;④当x<﹣2时,ax;其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共7小题,每小题4分,共28分)
11.(4分)计算:﹣ .
12.(4分)将直线y=﹣2x+3向下平移2个单位长度,平移后直线的解析式为 .
13.(4分)如图,平行四边形ABCD的周长为48,对角线AC,BD相交于点O,E是CD的中点,BD=16,则△DOE的周长是 .
14.(4分)甲、乙两名同学参加“古诗词大赛”活动,五次比赛成绩的平均分都是85分,如果甲比赛成绩的方差为S甲2=16.7,乙比赛成绩的方差为S乙2=28.3,那么成绩比较稳定的是 (填“甲”或“乙”)
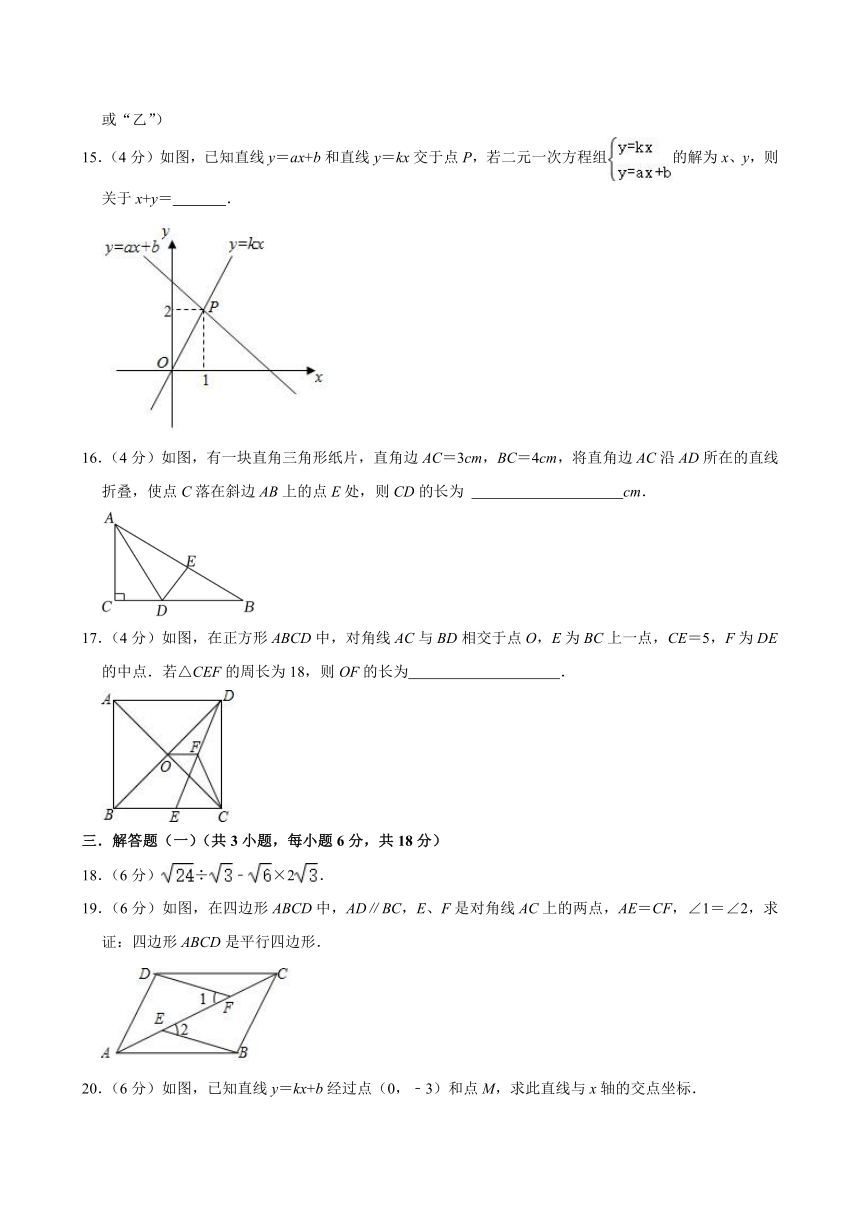
15.(4分)如图,已知直线y=ax+b和直线y=kx交于点P,若二元一次方程组的解为x、y,则关于x+y= .
16.(4分)如图,有一块直角三角形纸片,直角边AC=3cm,BC=4cm,将直角边AC沿AD所在的直线折叠,使点C落在斜边AB上的点E处,则CD的长为 cm.
17.(4分)如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为 .
三.解答题(一)(共3小题,每小题6分,共18分)
18.(6分)÷﹣×2.
19.(6分)如图,在四边形ABCD中,AD∥BC,E、F是对角线AC上的两点,AE=CF,∠1=∠2,求证:四边形ABCD是平行四边形.
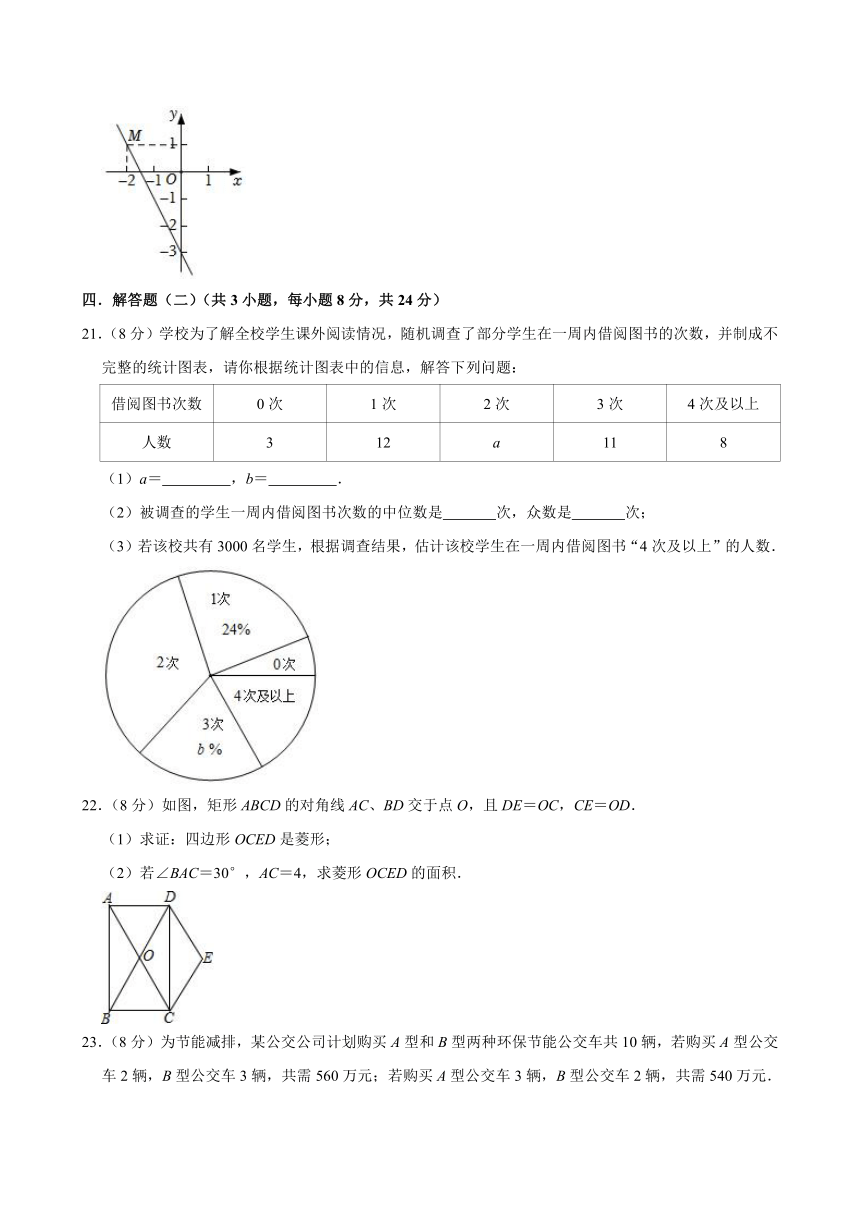
20.(6分)如图,已知直线y=kx+b经过点(0,﹣3)和点M,求此直线与x轴的交点坐标.
四.解答题(二)(共3小题,每小题8分,共24分)
21.(8分)学校为了解全校学生课外阅读情况,随机调查了部分学生在一周内借阅图书的次数,并制成不完整的统计图表,请你根据统计图表中的信息,解答下列问题:
借阅图书次数 0次 1次 2次 3次 4次及以上
人数 3 12 a 11 8
(1)a= ,b= .
(2)被调查的学生一周内借阅图书次数的中位数是 次,众数是 次;
(3)若该校共有3000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.
22.(8分)如图,矩形ABCD的对角线AC、BD交于点O,且DE=OC,CE=OD.
(1)求证:四边形OCED是菱形;
(2)若∠BAC=30°,AC=4,求菱形OCED的面积.
23.(8分)为节能减排,某公交公司计划购买A型和B型两种环保节能公交车共10辆,若购买A型公交车2辆,B型公交车3辆,共需560万元;若购买A型公交车3辆,B型公交车2辆,共需540万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该线路上A型和B型公交车每辆年均载客量分别为80万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1120万元,且确保这10辆公交车在该线路的年均载客总和不少于850万人次,则该公司有几种购车方案?请求出购车费用最少的方案?
五.解答题(三)(共2小题,每小题10分,共20分)
24.(10分)如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
25.(10分)如图(含备用图),在直角坐标系中,已知直线y=kx+3与x轴相交于点A(2,0),与y轴交于点B.
(1)求k的值及△AOB的面积;
(2)点C在x轴上,若△ABC是以AB为腰的等腰三角形,直接写出点C的坐标;
(3)点M(3,0)在x轴上,若点P是直线AB上的一个动点,当△PBM的面积与△AOB的面积相等时,求点P的坐标.
2021-2022学年广东省湛江市吴川市广大实验学校八年级(下)期末数学试卷
参考答案
一.选择题(共10小题,每小题3分,共30分)
1.(3分)如果有意义,那么x的取值范围是( )
A.x>1 B.x≥1 C.x≤1 D.x<1
选:B.
2.(3分)下列计算正确的是( )
A. B. C.3+2=5 D.=2
选:B.
3.(3分)下列各组数中,能构成直角三角形的是( )
A.4,5,6 B.6,8,11 C.1,1, D.5,12,10
选:C.
4.(3分)若函数y=x+k﹣2是正比例函数,则k的值是( )
A.6 B.4 C.2 D.﹣2
选:C.
5.(3分)如图,在平行四边形ABCD中,AE平分∠BAD,交CD边于E,AD=3,AB=5,则EC的长为( )
A.1 B.2 C.3 D.5
选:B.
6.(3分)如图,在矩形ABCD中,∠BOC=120°,AC=4,则AB的长为( )
A.2 B.4 C.2 D.4
选:A.
7.(3分)秦始皇兵马俑博物馆拟招聘一名优秀讲解员,张力的笔试、试讲、面试三轮测试成绩分别为90分、94分、92分.综合成绩中笔试占50%、试讲占30%、面试占20%,那么张力的最后得分为( )
A.91分 B.91.6分 C.92分 D.93分
选:B.
8.(3分)如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=3,AF=5,则AC的长为( )
A.4 B.4 C.10 D.8
选:A.
9.(3分)对于函数y=﹣2x﹣1,下列结论正确的是( )
A.它的图象必经过点(﹣1,0)
B.它的图象经过第一、二、三象限
C.当x>1时,y<0
D.y的值随x值的增大而增大
选:C.
10.(3分)如图,已知正比例函数与一次函数的图象交于点P,则以下结论:
①a>0;②2a+b=1;③当x<0时,y1>0;④当x<﹣2时,ax;其中正确的有( )
A.1个 B.2个 C.3个 D.4个
选:B.
二.填空题(共7小题,每小题4分,共28分)
11.(4分)计算:﹣ =
12.(4分)将直线y=﹣2x+3向下平移2个单位长度,平移后直线的解析式为 y=﹣2x+1 .
13.(4分)如图,平行四边形ABCD的周长为48,对角线AC,BD相交于点O,E是CD的中点,BD=16,则△DOE的周长是 20 .
14.(4分)甲、乙两名同学参加“古诗词大赛”活动,五次比赛成绩的平均分都是85分,如果甲比赛成绩的方差为S甲2=16.7,乙比赛成绩的方差为S乙2=28.3,那么成绩比较稳定的是 甲 (填“甲”或“乙”)
15.(4分)如图,已知直线y=ax+b和直线y=kx交于点P,若二元一次方程组的解为x、y,则关于x+y= 3 .
16.(4分)如图,有一块直角三角形纸片,直角边AC=3cm,BC=4cm,将直角边AC沿AD所在的直线折叠,使点C落在斜边AB上的点E处,则CD的长为 cm.
17.(4分)如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为 .
三.解答题(一)(共3小题,每小题6分,共18分)
18.(6分)÷﹣×2.
【解答】解:原式=2﹣6
=﹣4.
19.(6分)如图,在四边形ABCD中,AD∥BC,E、F是对角线AC上的两点,AE=CF,∠1=∠2,求证:四边形ABCD是平行四边形.
【解答】证明:∵AD∥BC,
∴∠DAF=∠BCE,
∵AE=CF,
∴AE+EF=CF+EF,
即AF=CE,
∵∠1=∠2,
在△ADF和△CBE中,,
∴△ADF≌△CBE(ASA),
∴AD=BC,
∴四边形ABCD是平行四边形.
20.(6分)如图,已知直线y=kx+b经过点(0,﹣3)和点M,求此直线与x轴的交点坐标.
【解答】解:将(0,﹣3),(﹣2,1)代入y=kx+b得:,
解得:,
∴直线的函数关系式为y=﹣2x﹣3.
当y=0时,﹣2x﹣3=0,
解得:x=﹣,
∴此直线与x轴的交点坐标为(﹣,0).
四.解答题(二)(共3小题,每小题8分,共24分)
21.(8分)学校为了解全校学生课外阅读情况,随机调查了部分学生在一周内借阅图书的次数,并制成不完整的统计图表,请你根据统计图表中的信息,解答下列问题:
借阅图书次数 0次 1次 2次 3次 4次及以上
人数 3 12 a 11 8
(1)a= 16 ,b= 22 .
(2)被调查的学生一周内借阅图书次数的中位数是 2 次,众数是 2 次;
(3)若该校共有3000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.
【解答】解:(1)本次调查的总人数为:12÷24%=50(人),
∴a=50﹣(3+12+11+8)=16(人),
b%=×100%=22%,即b=22,
故答案为:16、22;
(2)该调查统计数据的中位数是=2(次),众数为2次,
故答案为:2,2;
(3)该校学生在一周内借阅图书“4次及以上”的人数有3000×=480(人).
22.(8分)如图,矩形ABCD的对角线AC、BD交于点O,且DE=OC,CE=OD.
(1)求证:四边形OCED是菱形;
(2)若∠BAC=30°,AC=4,求菱形OCED的面积.
【解答】(1)证明:∵DE=OC,CE=OD,
∴四边形OCED是平行四边形,
∵矩形ABCD,
∴AC=BD,OC=AC,OD=BD,
∴OC=OD,
∴平行四边形OCED是菱形.
(2)解:在矩形ABCD中,∠ABC=90°,∠BAC=30°,AC=4,
∴BC=2,
∴AB=DC=,
连接OE,交CD于点F.
∵四边形OCED为菱形,
∴F为CD中点,
∵O为BD中点,
∴OF=BC=1,
∴OE=2OF=2,
∴S菱形OCED=OE CD=×2×=.
23.(8分)为节能减排,某公交公司计划购买A型和B型两种环保节能公交车共10辆,若购买A型公交车2辆,B型公交车3辆,共需560万元;若购买A型公交车3辆,B型公交车2辆,共需540万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该线路上A型和B型公交车每辆年均载客量分别为80万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1120万元,且确保这10辆公交车在该线路的年均载客总和不少于850万人次,则该公司有几种购车方案?请求出购车费用最少的方案?
【解答】解:(1)设购买A型公交车每辆需x万元,购买B型公交车每辆需y万元,
由题知:,
解得,
答:A型公交车每辆需100万元,B型公交车每辆需120万元;
(2)设购买A型公交车m辆,购买B型公交车(10﹣m)辆,
根据题意得:,
∴4≤m≤,且m为正整数,
∴m=4,5,6,7,一共有4种采购方案;
设总费用为w万元,
w=100m+120(10﹣m)=﹣20m+1200,
∵﹣20<0,
∴w随m的增大而减小,
又4≤m≤,且m为正整数,
∴当m=7时,w最小,最小值是1060万元;
答:该公司有4种购车方案,当采购A型7辆,采购B型3辆时,费用最低,最低费用为1060万元.
五.解答题(三)(共2小题,每小题10分,共20分)
24.(10分)如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
【解答】(1)证明:在正方形ABCD中,AB=BC,
∠ABP=∠CBP=45°,
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,
∵PA=PE,
∴PC=PE;
(2)由(1)知,△ABP≌△CBP,
∴∠BAP=∠BCP,
∴∠DAP=∠DCP,
∵PA=PE,
∴∠DAP=∠E,
∴∠DCP=∠E,
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,
即∠CPF=∠EDF=90°;
(3)在菱形ABCD中,AB=BC,∠ABP=∠CBP,
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,∠BAP=∠BCP,∴∠DAP=∠DCP,
∵PA=PE,∴PC=PE,
∵PA=PE,∴∠DAP=∠DEP,∴∠DCP=∠DEP,
∵∠CFP=∠EFD,∴∠CPF=∠EDF
∵∠ABC=∠ADC=120°,
∴∠CPF=∠EDF=180°﹣∠ADC=60°,
∴△EPC是等边三角形,
∴PC=CE,
∴AP=CE;
25.(10分)如图(含备用图),在直角坐标系中,已知直线y=kx+3与x轴相交于点A(2,0),与y轴交于点B.
(1)求k的值及△AOB的面积;
(2)点C在x轴上,若△ABC是以AB为腰的等腰三角形,直接写出点C的坐标;
(3)点M(3,0)在x轴上,若点P是直线AB上的一个动点,当△PBM的面积与△AOB的面积相等时,求点P的坐标.
【解答】解:(1)将点A(2,0)代入直线y=kx+3,得
0=2k+3,
解得k=﹣,
∴y=﹣x+3.
当x=0时,y=3.
∴B(0,3),OB=3.
当y=0时,﹣x+3=0,
∴x=2,
∴A(2,0),OA=2,
∴S△AOB=OA OB=×2×3=3.
(2)如图2,
①当AB=BC时,点C与点A(2,0)关于y轴对称,故C(﹣2,0)符合题意;
②当AB=AC时,由A(2,0),B(0,3)得到AB==,由AC=AC′=得到C′(+2,0)、C″(2﹣,0).
综上所述,符合条件的点C的坐标是(﹣2,0)或(+2,0)或(2﹣,0);
(3)∵M(3,0),
∴OM=3,
∴AM=3﹣2=1.
由(1)知,S△AOB=3,
∴S△PBM=S△AOB=3;
①当点P在x轴下方时,S△PBM=S△PAM+S△ABM=+ AM |yP|=+×1×|yP|=3,
∴|yP|=3,
∵点P在x轴下方,
∴yP=﹣3.
当y=﹣3时,代入y=﹣x+3得,﹣3=﹣x+3,
解得x=4.
∴P(4,﹣3);
②当点P在x轴上方时,S△PBM=S△APM﹣S△ABM= AM |yP|﹣=×1×|yP|﹣=3,
∴|yP|=9,
∵点P在x轴上方,
∴yP=9.
当y=9时,代入y=﹣x+3得,9=﹣x+3,
解得x=﹣4.
∴P(﹣4,9).
一.选择题(共10小题,每小题3分,共30分)
1.(3分)如果有意义,那么x的取值范围是( )
A.x>1 B.x≥1 C.x≤1 D.x<1
2.(3分)下列计算正确的是( )
A. B. C.3+2=5 D.=2
3.(3分)下列各组数中,能构成直角三角形的是( )
A.4,5,6 B.6,8,11 C.1,1, D.5,12,10
4.(3分)若函数y=x+k﹣2是正比例函数,则k的值是( )
A.6 B.4 C.2 D.﹣2
5.(3分)如图,在平行四边形ABCD中,AE平分∠BAD,交CD边于E,AD=3,AB=5,则EC的长为( )
A.1 B.2 C.3 D.5
6.(3分)如图,在矩形ABCD中,∠BOC=120°,AC=4,则AB的长为( )
A.2 B.4 C.2 D.4
7.(3分)秦始皇兵马俑博物馆拟招聘一名优秀讲解员,张力的笔试、试讲、面试三轮测试成绩分别为90分、94分、92分.综合成绩中笔试占50%、试讲占30%、面试占20%,那么张力的最后得分为( )
A.91分 B.91.6分 C.92分 D.93分
8.(3分)如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=3,AF=5,则AC的长为( )
A.4 B.4 C.10 D.8
9.(3分)对于函数y=﹣2x﹣1,下列结论正确的是( )
A.它的图象必经过点(﹣1,0)
B.它的图象经过第一、二、三象限
C.当x>1时,y<0
D.y的值随x值的增大而增大
10.(3分)如图,已知正比例函数与一次函数的图象交于点P,则以下结论:
①a>0;②2a+b=1;③当x<0时,y1>0;④当x<﹣2时,ax;其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共7小题,每小题4分,共28分)
11.(4分)计算:﹣ .
12.(4分)将直线y=﹣2x+3向下平移2个单位长度,平移后直线的解析式为 .
13.(4分)如图,平行四边形ABCD的周长为48,对角线AC,BD相交于点O,E是CD的中点,BD=16,则△DOE的周长是 .
14.(4分)甲、乙两名同学参加“古诗词大赛”活动,五次比赛成绩的平均分都是85分,如果甲比赛成绩的方差为S甲2=16.7,乙比赛成绩的方差为S乙2=28.3,那么成绩比较稳定的是 (填“甲”或“乙”)
15.(4分)如图,已知直线y=ax+b和直线y=kx交于点P,若二元一次方程组的解为x、y,则关于x+y= .
16.(4分)如图,有一块直角三角形纸片,直角边AC=3cm,BC=4cm,将直角边AC沿AD所在的直线折叠,使点C落在斜边AB上的点E处,则CD的长为 cm.
17.(4分)如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为 .
三.解答题(一)(共3小题,每小题6分,共18分)
18.(6分)÷﹣×2.
19.(6分)如图,在四边形ABCD中,AD∥BC,E、F是对角线AC上的两点,AE=CF,∠1=∠2,求证:四边形ABCD是平行四边形.
20.(6分)如图,已知直线y=kx+b经过点(0,﹣3)和点M,求此直线与x轴的交点坐标.
四.解答题(二)(共3小题,每小题8分,共24分)
21.(8分)学校为了解全校学生课外阅读情况,随机调查了部分学生在一周内借阅图书的次数,并制成不完整的统计图表,请你根据统计图表中的信息,解答下列问题:
借阅图书次数 0次 1次 2次 3次 4次及以上
人数 3 12 a 11 8
(1)a= ,b= .
(2)被调查的学生一周内借阅图书次数的中位数是 次,众数是 次;
(3)若该校共有3000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.
22.(8分)如图,矩形ABCD的对角线AC、BD交于点O,且DE=OC,CE=OD.
(1)求证:四边形OCED是菱形;
(2)若∠BAC=30°,AC=4,求菱形OCED的面积.
23.(8分)为节能减排,某公交公司计划购买A型和B型两种环保节能公交车共10辆,若购买A型公交车2辆,B型公交车3辆,共需560万元;若购买A型公交车3辆,B型公交车2辆,共需540万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该线路上A型和B型公交车每辆年均载客量分别为80万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1120万元,且确保这10辆公交车在该线路的年均载客总和不少于850万人次,则该公司有几种购车方案?请求出购车费用最少的方案?
五.解答题(三)(共2小题,每小题10分,共20分)
24.(10分)如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
25.(10分)如图(含备用图),在直角坐标系中,已知直线y=kx+3与x轴相交于点A(2,0),与y轴交于点B.
(1)求k的值及△AOB的面积;
(2)点C在x轴上,若△ABC是以AB为腰的等腰三角形,直接写出点C的坐标;
(3)点M(3,0)在x轴上,若点P是直线AB上的一个动点,当△PBM的面积与△AOB的面积相等时,求点P的坐标.
2021-2022学年广东省湛江市吴川市广大实验学校八年级(下)期末数学试卷
参考答案
一.选择题(共10小题,每小题3分,共30分)
1.(3分)如果有意义,那么x的取值范围是( )
A.x>1 B.x≥1 C.x≤1 D.x<1
选:B.
2.(3分)下列计算正确的是( )
A. B. C.3+2=5 D.=2
选:B.
3.(3分)下列各组数中,能构成直角三角形的是( )
A.4,5,6 B.6,8,11 C.1,1, D.5,12,10
选:C.
4.(3分)若函数y=x+k﹣2是正比例函数,则k的值是( )
A.6 B.4 C.2 D.﹣2
选:C.
5.(3分)如图,在平行四边形ABCD中,AE平分∠BAD,交CD边于E,AD=3,AB=5,则EC的长为( )
A.1 B.2 C.3 D.5
选:B.
6.(3分)如图,在矩形ABCD中,∠BOC=120°,AC=4,则AB的长为( )
A.2 B.4 C.2 D.4
选:A.
7.(3分)秦始皇兵马俑博物馆拟招聘一名优秀讲解员,张力的笔试、试讲、面试三轮测试成绩分别为90分、94分、92分.综合成绩中笔试占50%、试讲占30%、面试占20%,那么张力的最后得分为( )
A.91分 B.91.6分 C.92分 D.93分
选:B.
8.(3分)如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=3,AF=5,则AC的长为( )
A.4 B.4 C.10 D.8
选:A.
9.(3分)对于函数y=﹣2x﹣1,下列结论正确的是( )
A.它的图象必经过点(﹣1,0)
B.它的图象经过第一、二、三象限
C.当x>1时,y<0
D.y的值随x值的增大而增大
选:C.
10.(3分)如图,已知正比例函数与一次函数的图象交于点P,则以下结论:
①a>0;②2a+b=1;③当x<0时,y1>0;④当x<﹣2时,ax;其中正确的有( )
A.1个 B.2个 C.3个 D.4个
选:B.
二.填空题(共7小题,每小题4分,共28分)
11.(4分)计算:﹣ =
12.(4分)将直线y=﹣2x+3向下平移2个单位长度,平移后直线的解析式为 y=﹣2x+1 .
13.(4分)如图,平行四边形ABCD的周长为48,对角线AC,BD相交于点O,E是CD的中点,BD=16,则△DOE的周长是 20 .
14.(4分)甲、乙两名同学参加“古诗词大赛”活动,五次比赛成绩的平均分都是85分,如果甲比赛成绩的方差为S甲2=16.7,乙比赛成绩的方差为S乙2=28.3,那么成绩比较稳定的是 甲 (填“甲”或“乙”)
15.(4分)如图,已知直线y=ax+b和直线y=kx交于点P,若二元一次方程组的解为x、y,则关于x+y= 3 .
16.(4分)如图,有一块直角三角形纸片,直角边AC=3cm,BC=4cm,将直角边AC沿AD所在的直线折叠,使点C落在斜边AB上的点E处,则CD的长为 cm.
17.(4分)如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为 .
三.解答题(一)(共3小题,每小题6分,共18分)
18.(6分)÷﹣×2.
【解答】解:原式=2﹣6
=﹣4.
19.(6分)如图,在四边形ABCD中,AD∥BC,E、F是对角线AC上的两点,AE=CF,∠1=∠2,求证:四边形ABCD是平行四边形.
【解答】证明:∵AD∥BC,
∴∠DAF=∠BCE,
∵AE=CF,
∴AE+EF=CF+EF,
即AF=CE,
∵∠1=∠2,
在△ADF和△CBE中,,
∴△ADF≌△CBE(ASA),
∴AD=BC,
∴四边形ABCD是平行四边形.
20.(6分)如图,已知直线y=kx+b经过点(0,﹣3)和点M,求此直线与x轴的交点坐标.
【解答】解:将(0,﹣3),(﹣2,1)代入y=kx+b得:,
解得:,
∴直线的函数关系式为y=﹣2x﹣3.
当y=0时,﹣2x﹣3=0,
解得:x=﹣,
∴此直线与x轴的交点坐标为(﹣,0).
四.解答题(二)(共3小题,每小题8分,共24分)
21.(8分)学校为了解全校学生课外阅读情况,随机调查了部分学生在一周内借阅图书的次数,并制成不完整的统计图表,请你根据统计图表中的信息,解答下列问题:
借阅图书次数 0次 1次 2次 3次 4次及以上
人数 3 12 a 11 8
(1)a= 16 ,b= 22 .
(2)被调查的学生一周内借阅图书次数的中位数是 2 次,众数是 2 次;
(3)若该校共有3000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.
【解答】解:(1)本次调查的总人数为:12÷24%=50(人),
∴a=50﹣(3+12+11+8)=16(人),
b%=×100%=22%,即b=22,
故答案为:16、22;
(2)该调查统计数据的中位数是=2(次),众数为2次,
故答案为:2,2;
(3)该校学生在一周内借阅图书“4次及以上”的人数有3000×=480(人).
22.(8分)如图,矩形ABCD的对角线AC、BD交于点O,且DE=OC,CE=OD.
(1)求证:四边形OCED是菱形;
(2)若∠BAC=30°,AC=4,求菱形OCED的面积.
【解答】(1)证明:∵DE=OC,CE=OD,
∴四边形OCED是平行四边形,
∵矩形ABCD,
∴AC=BD,OC=AC,OD=BD,
∴OC=OD,
∴平行四边形OCED是菱形.
(2)解:在矩形ABCD中,∠ABC=90°,∠BAC=30°,AC=4,
∴BC=2,
∴AB=DC=,
连接OE,交CD于点F.
∵四边形OCED为菱形,
∴F为CD中点,
∵O为BD中点,
∴OF=BC=1,
∴OE=2OF=2,
∴S菱形OCED=OE CD=×2×=.
23.(8分)为节能减排,某公交公司计划购买A型和B型两种环保节能公交车共10辆,若购买A型公交车2辆,B型公交车3辆,共需560万元;若购买A型公交车3辆,B型公交车2辆,共需540万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该线路上A型和B型公交车每辆年均载客量分别为80万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1120万元,且确保这10辆公交车在该线路的年均载客总和不少于850万人次,则该公司有几种购车方案?请求出购车费用最少的方案?
【解答】解:(1)设购买A型公交车每辆需x万元,购买B型公交车每辆需y万元,
由题知:,
解得,
答:A型公交车每辆需100万元,B型公交车每辆需120万元;
(2)设购买A型公交车m辆,购买B型公交车(10﹣m)辆,
根据题意得:,
∴4≤m≤,且m为正整数,
∴m=4,5,6,7,一共有4种采购方案;
设总费用为w万元,
w=100m+120(10﹣m)=﹣20m+1200,
∵﹣20<0,
∴w随m的增大而减小,
又4≤m≤,且m为正整数,
∴当m=7时,w最小,最小值是1060万元;
答:该公司有4种购车方案,当采购A型7辆,采购B型3辆时,费用最低,最低费用为1060万元.
五.解答题(三)(共2小题,每小题10分,共20分)
24.(10分)如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
【解答】(1)证明:在正方形ABCD中,AB=BC,
∠ABP=∠CBP=45°,
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,
∵PA=PE,
∴PC=PE;
(2)由(1)知,△ABP≌△CBP,
∴∠BAP=∠BCP,
∴∠DAP=∠DCP,
∵PA=PE,
∴∠DAP=∠E,
∴∠DCP=∠E,
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,
即∠CPF=∠EDF=90°;
(3)在菱形ABCD中,AB=BC,∠ABP=∠CBP,
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,∠BAP=∠BCP,∴∠DAP=∠DCP,
∵PA=PE,∴PC=PE,
∵PA=PE,∴∠DAP=∠DEP,∴∠DCP=∠DEP,
∵∠CFP=∠EFD,∴∠CPF=∠EDF
∵∠ABC=∠ADC=120°,
∴∠CPF=∠EDF=180°﹣∠ADC=60°,
∴△EPC是等边三角形,
∴PC=CE,
∴AP=CE;
25.(10分)如图(含备用图),在直角坐标系中,已知直线y=kx+3与x轴相交于点A(2,0),与y轴交于点B.
(1)求k的值及△AOB的面积;
(2)点C在x轴上,若△ABC是以AB为腰的等腰三角形,直接写出点C的坐标;
(3)点M(3,0)在x轴上,若点P是直线AB上的一个动点,当△PBM的面积与△AOB的面积相等时,求点P的坐标.
【解答】解:(1)将点A(2,0)代入直线y=kx+3,得
0=2k+3,
解得k=﹣,
∴y=﹣x+3.
当x=0时,y=3.
∴B(0,3),OB=3.
当y=0时,﹣x+3=0,
∴x=2,
∴A(2,0),OA=2,
∴S△AOB=OA OB=×2×3=3.
(2)如图2,
①当AB=BC时,点C与点A(2,0)关于y轴对称,故C(﹣2,0)符合题意;
②当AB=AC时,由A(2,0),B(0,3)得到AB==,由AC=AC′=得到C′(+2,0)、C″(2﹣,0).
综上所述,符合条件的点C的坐标是(﹣2,0)或(+2,0)或(2﹣,0);
(3)∵M(3,0),
∴OM=3,
∴AM=3﹣2=1.
由(1)知,S△AOB=3,
∴S△PBM=S△AOB=3;
①当点P在x轴下方时,S△PBM=S△PAM+S△ABM=+ AM |yP|=+×1×|yP|=3,
∴|yP|=3,
∵点P在x轴下方,
∴yP=﹣3.
当y=﹣3时,代入y=﹣x+3得,﹣3=﹣x+3,
解得x=4.
∴P(4,﹣3);
②当点P在x轴上方时,S△PBM=S△APM﹣S△ABM= AM |yP|﹣=×1×|yP|﹣=3,
∴|yP|=9,
∵点P在x轴上方,
∴yP=9.
当y=9时,代入y=﹣x+3得,9=﹣x+3,
解得x=﹣4.
∴P(﹣4,9).
同课章节目录
