第二章 直角三角形的边角关系 6 利用三角函数测高(含答案)
文档属性
| 名称 | 第二章 直角三角形的边角关系 6 利用三角函数测高(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 7.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-31 05:40:20 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二章 直角三角形的边角关系
6 利用三角函数测高
1.如图,一枚运载火箭从地面 L 处发射,雷达站 R 与发射点 L 之间的距离为6千米,当火箭到达 A点时,雷达站测得仰角为α,则这枚火箭此时的高度AL 为 ( )
千米
第1题图 第2题图
2.如图,距离地面高m米的A 处,用测角仪测得树顶端C 点的仰角为α,测得树底端D点的俯角为45°,则树CD的高为 ( )
米
3.如图是某商场营业大厅自动扶梯示意图.自动扶梯AB 的倾斜角为30°,在自动扶梯下方地面 C 处测得扶梯顶端B 的仰角为60°,点 A,C 之间的距离为4 m .则自动扶梯的垂直高度 BD 约为(保留一位小数, ( )
A.3.9米 B.3.7米 C.3.5米 D.3.3米
4.如图,甲乙两楼相距 30 米,乙楼高度为 36 米,自甲楼顶 A 处看乙楼楼顶B 处仰角为 则甲楼高度为( )
A.15米 米 米 米
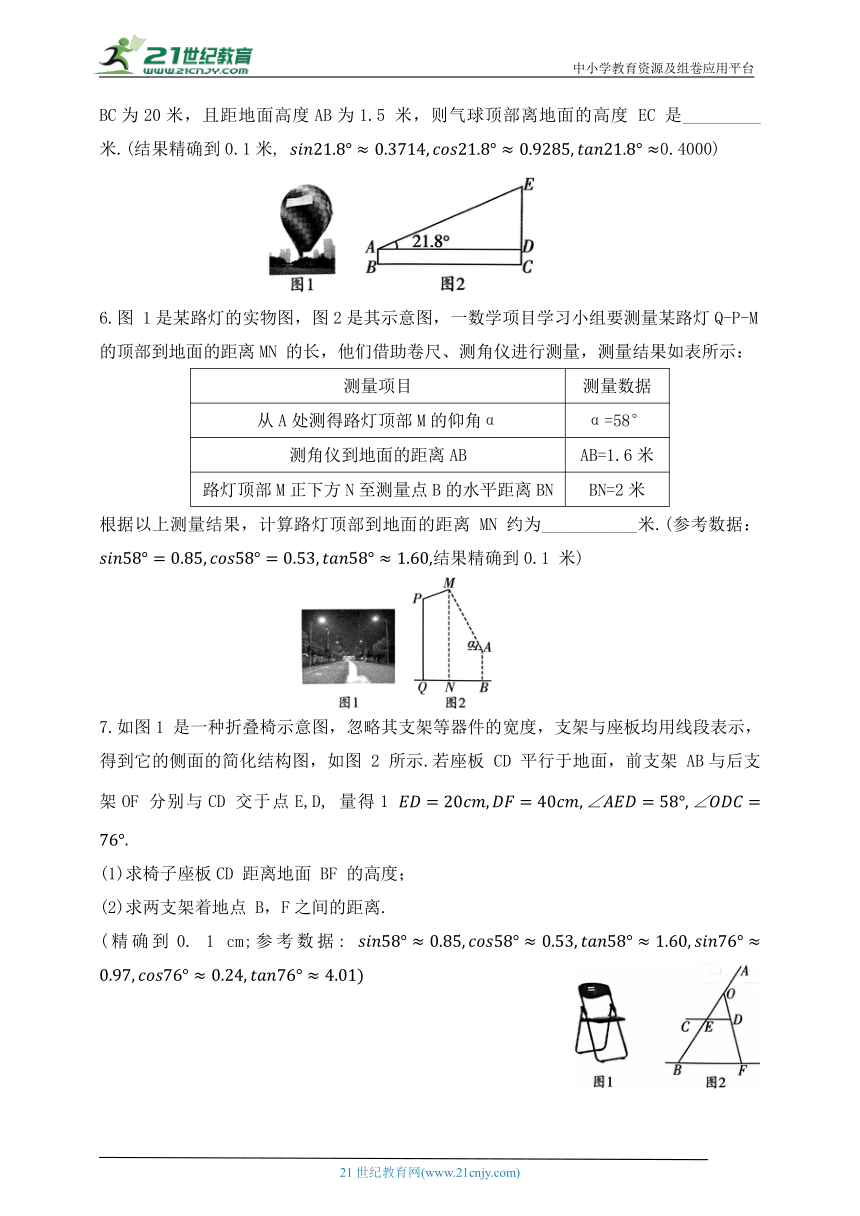
5.2023年岳阳市举办了以“跃马江湖”为主题的马拉松赛事.如图,某校数学兴趣小组在 A 处用仪器测得赛场一宣传气球顶部E 处的仰角为21.8°,仪器与气球的水平距离 BC为20米,且距地面高度AB为1.5 米,则气球顶部离地面的高度 EC 是_________米.(结果精确到0.1米, 0.4000)
6.图 1是某路灯的实物图,图2是其示意图,一数学项目学习小组要测量某路灯Q-P-M的顶部到地面的距离MN 的长,他们借助卷尺、测角仪进行测量,测量结果如表所示:
测量项目 测量数据
从A处测得路灯顶部M的仰角α α=58°
测角仪到地面的距离AB AB=1.6米
路灯顶部M正下方N至测量点B的水平距离BN BN=2米
根据以上测量结果,计算路灯顶部到地面的距离 MN 约为___________米.(参考数据:结果精确到0.1 米)
7.如图1 是一种折叠椅示意图,忽略其支架等器件的宽度,支架与座板均用线段表示,得到它的侧面的简化结构图,如图 2 所示.若座板 CD 平行于地面,前支架 AB与后支架OF 分别与CD 交于点E,D, 量得1
(1)求椅子座板CD 距离地面 BF 的高度;
(2)求两支架着地点 B,F之间的距离.
(精确到0. 1 cm;参考数据:
8.在综合与实践活动中,要利用测角仪测量塔的高度.如图,塔AB前有一座高为 3m 的观景台 DE,已知 点E,C,A 在同一条水平直线上.某学习小组在观景台C 处测得塔顶部 B 的仰角为 在观景台 D 处测得塔顶部B 的仰角为 求塔 AB的高度.(参考数据:
9.如图,AB 是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走 20米到达点C,再经过一段坡度(或坡比)为 0.75、坡长为10米的斜坡CD到达点 D,然后再沿水平方向向右行走 40 米到达点 E(点 A,B,C,D,E均在同一平面内),在 E 处测得建筑物顶端 A 的仰角为 则建筑物AB 的高度约为_________米.(参考数据:
参考答案
1. C 2. A 3. C 4. B
5.9.5 6.4.8
7.解:(1)过点 E,D 分别作 EH⊥BF 于点 H, DG⊥BF 于点G,
∴∠EHB=∠DGF=90°,
∵ED∥BF,∴∠OED=∠EBH=58°,∠ODE=∠DFG=76°,
在 Rt △DGF 中, DF =40 cm,
∴DG=0.97×40=38.8(cm),
所以,椅子座板 CD 距离地面 BF 的高度是38.8cm ;
(2)在 Rt△DGF中,DF=40 cm,
∴FG=0.24×40=9.6(cm),
∵ED∥BF,EH⊥BF,DG⊥BF,∴四边形 EDHG 是矩形,
∴EH=DG=38.8cm,ED=HG=20cm,
在 Rt△EBH中,EH=38.8cm ,
∴BH≈24.25(cm),
∴BF=BH+HG+GF=24.25+20+9.6=53.85≈53.9(cm),
所以,两支架着地点 BF 之间的距离约为
9 cm.
8.解:由题意,得 DE⊥EC,
在 Rt△DEC中,∠DCE=30°,∠DEC=90°,DE=3m,∴CE= DE=3 m,
∵BA⊥EA,在 Rt△ABC中,∠BCA=45°,设AB=h m,
,
过点 D 作 DF⊥AB 于点 F,
由题意,得.
∵AB=h m,
在 中,
所以,塔AB 的高度约为 11.1m .
21.7
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二章 直角三角形的边角关系
6 利用三角函数测高
1.如图,一枚运载火箭从地面 L 处发射,雷达站 R 与发射点 L 之间的距离为6千米,当火箭到达 A点时,雷达站测得仰角为α,则这枚火箭此时的高度AL 为 ( )
千米
第1题图 第2题图
2.如图,距离地面高m米的A 处,用测角仪测得树顶端C 点的仰角为α,测得树底端D点的俯角为45°,则树CD的高为 ( )
米
3.如图是某商场营业大厅自动扶梯示意图.自动扶梯AB 的倾斜角为30°,在自动扶梯下方地面 C 处测得扶梯顶端B 的仰角为60°,点 A,C 之间的距离为4 m .则自动扶梯的垂直高度 BD 约为(保留一位小数, ( )
A.3.9米 B.3.7米 C.3.5米 D.3.3米
4.如图,甲乙两楼相距 30 米,乙楼高度为 36 米,自甲楼顶 A 处看乙楼楼顶B 处仰角为 则甲楼高度为( )
A.15米 米 米 米
5.2023年岳阳市举办了以“跃马江湖”为主题的马拉松赛事.如图,某校数学兴趣小组在 A 处用仪器测得赛场一宣传气球顶部E 处的仰角为21.8°,仪器与气球的水平距离 BC为20米,且距地面高度AB为1.5 米,则气球顶部离地面的高度 EC 是_________米.(结果精确到0.1米, 0.4000)
6.图 1是某路灯的实物图,图2是其示意图,一数学项目学习小组要测量某路灯Q-P-M的顶部到地面的距离MN 的长,他们借助卷尺、测角仪进行测量,测量结果如表所示:
测量项目 测量数据
从A处测得路灯顶部M的仰角α α=58°
测角仪到地面的距离AB AB=1.6米
路灯顶部M正下方N至测量点B的水平距离BN BN=2米
根据以上测量结果,计算路灯顶部到地面的距离 MN 约为___________米.(参考数据:结果精确到0.1 米)
7.如图1 是一种折叠椅示意图,忽略其支架等器件的宽度,支架与座板均用线段表示,得到它的侧面的简化结构图,如图 2 所示.若座板 CD 平行于地面,前支架 AB与后支架OF 分别与CD 交于点E,D, 量得1
(1)求椅子座板CD 距离地面 BF 的高度;
(2)求两支架着地点 B,F之间的距离.
(精确到0. 1 cm;参考数据:
8.在综合与实践活动中,要利用测角仪测量塔的高度.如图,塔AB前有一座高为 3m 的观景台 DE,已知 点E,C,A 在同一条水平直线上.某学习小组在观景台C 处测得塔顶部 B 的仰角为 在观景台 D 处测得塔顶部B 的仰角为 求塔 AB的高度.(参考数据:
9.如图,AB 是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走 20米到达点C,再经过一段坡度(或坡比)为 0.75、坡长为10米的斜坡CD到达点 D,然后再沿水平方向向右行走 40 米到达点 E(点 A,B,C,D,E均在同一平面内),在 E 处测得建筑物顶端 A 的仰角为 则建筑物AB 的高度约为_________米.(参考数据:
参考答案
1. C 2. A 3. C 4. B
5.9.5 6.4.8
7.解:(1)过点 E,D 分别作 EH⊥BF 于点 H, DG⊥BF 于点G,
∴∠EHB=∠DGF=90°,
∵ED∥BF,∴∠OED=∠EBH=58°,∠ODE=∠DFG=76°,
在 Rt △DGF 中, DF =40 cm,
∴DG=0.97×40=38.8(cm),
所以,椅子座板 CD 距离地面 BF 的高度是38.8cm ;
(2)在 Rt△DGF中,DF=40 cm,
∴FG=0.24×40=9.6(cm),
∵ED∥BF,EH⊥BF,DG⊥BF,∴四边形 EDHG 是矩形,
∴EH=DG=38.8cm,ED=HG=20cm,
在 Rt△EBH中,EH=38.8cm ,
∴BH≈24.25(cm),
∴BF=BH+HG+GF=24.25+20+9.6=53.85≈53.9(cm),
所以,两支架着地点 BF 之间的距离约为
9 cm.
8.解:由题意,得 DE⊥EC,
在 Rt△DEC中,∠DCE=30°,∠DEC=90°,DE=3m,∴CE= DE=3 m,
∵BA⊥EA,在 Rt△ABC中,∠BCA=45°,设AB=h m,
,
过点 D 作 DF⊥AB 于点 F,
由题意,得.
∵AB=h m,
在 中,
所以,塔AB 的高度约为 11.1m .
21.7
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
