第二章 直角三角形的边角关系 章末突破(含答案)
文档属性
| 名称 | 第二章 直角三角形的边角关系 章末突破(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 8.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-31 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第二章 直角三角形的边角关系
章末突破
类型一 锐角三角函数的定义
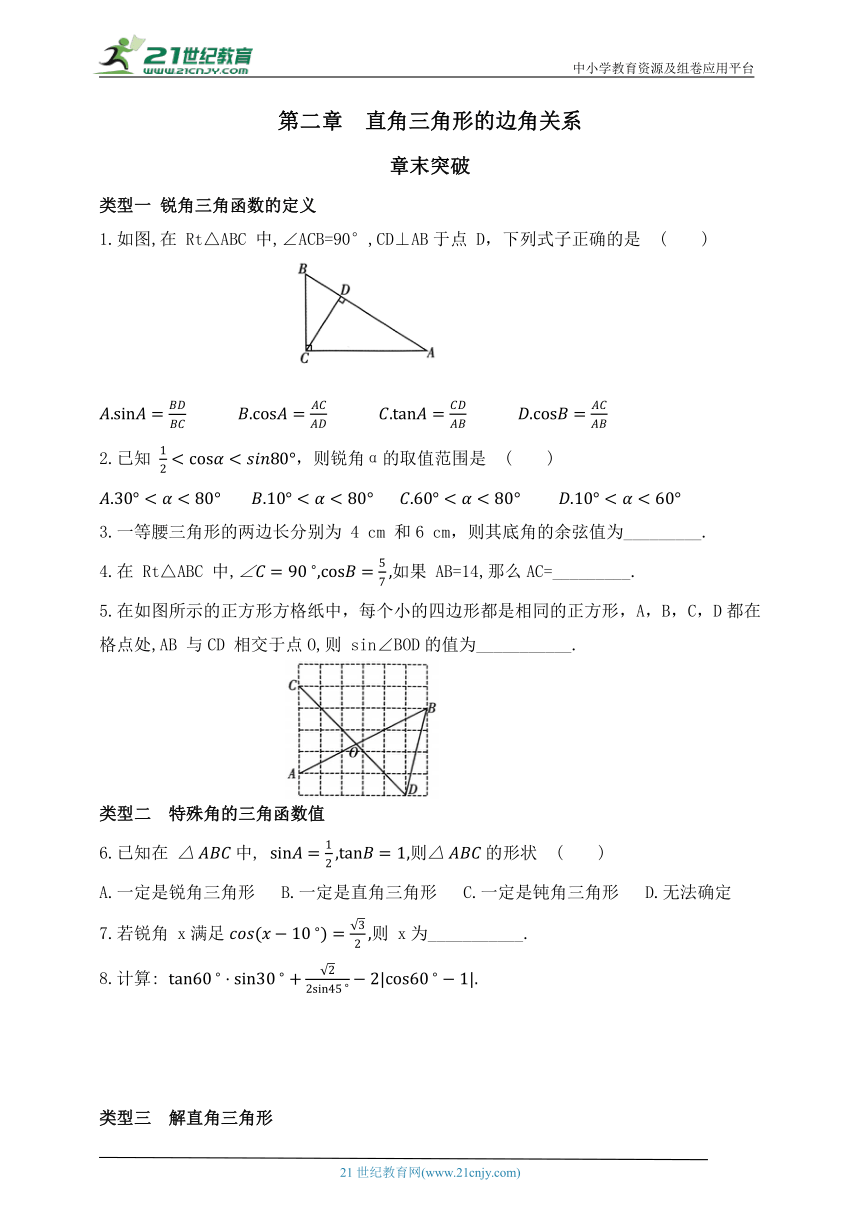
1.如图,在 Rt△ABC 中,∠ACB=90°,CD⊥AB于点 D,下列式子正确的是 ( )
2.已知 ,则锐角α的取值范围是 ( )
3.一等腰三角形的两边长分别为 4 cm 和6 cm,则其底角的余弦值为_________.
4.在 Rt△ABC 中,如果 AB=14,那么AC=_________.
5.在如图所示的正方形方格纸中,每个小的四边形都是相同的正方形,A,B,C,D都在格点处,AB 与CD 相交于点O,则 sin∠BOD的值为___________.
类型二 特殊角的三角函数值
6.已知在 中, 则的形状 ( )
A.一定是锐角三角形 B.一定是直角三角形 C.一定是钝角三角形 D.无法确定
7.若锐角 x满足则 x为___________.
8.计算:
类型三 解直角三角形
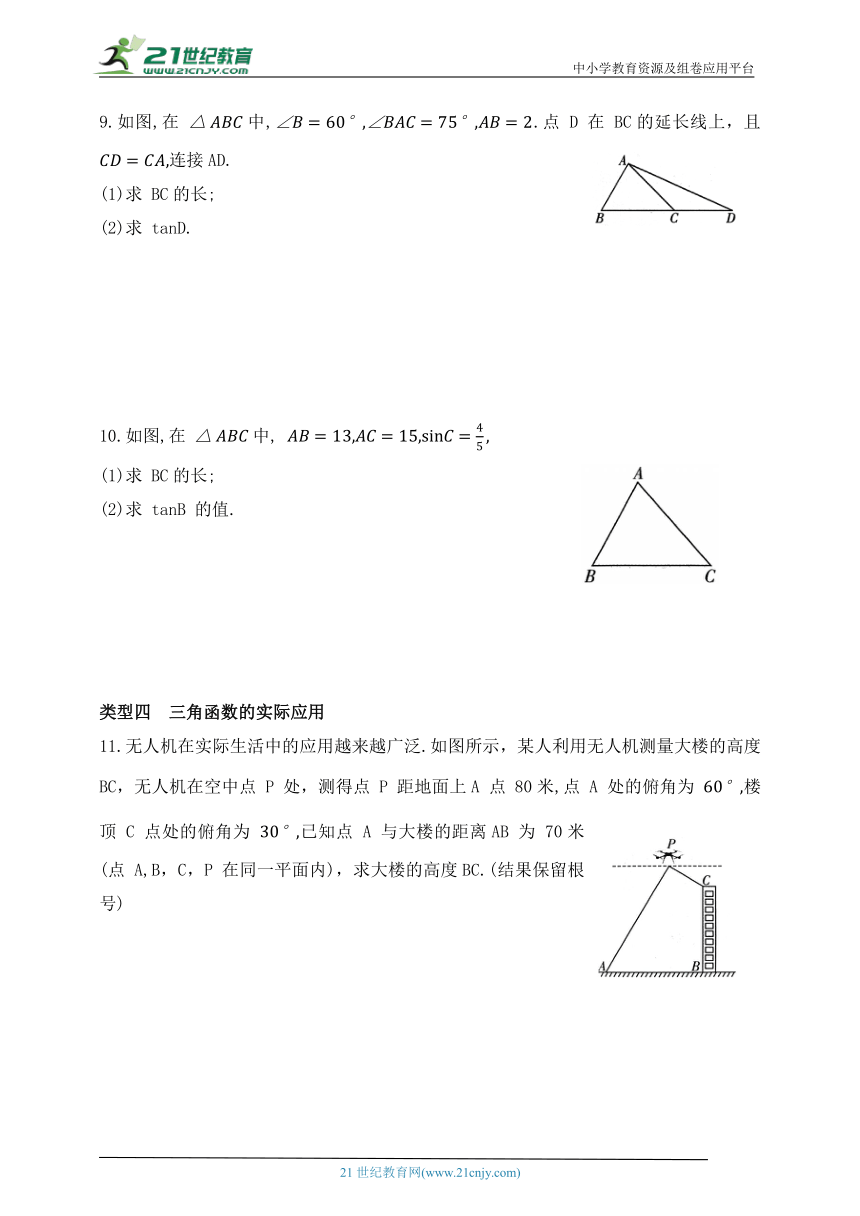
9.如图,在 中,.点 D 在 BC的延长线上,且 连接AD.
(1)求 BC的长;
(2)求 tanD.
10.如图,在 中,
(1)求 BC的长;
(2)求 tanB 的值.
类型四 三角函数的实际应用
11.无人机在实际生活中的应用越来越广泛.如图所示,某人利用无人机测量大楼的高度 BC,无人机在空中点 P 处,测得点 P 距地面上A 点 80米,点 A 处的俯角为 楼顶 C 点处的俯角为 已知点 A 与大楼的距离AB 为 70米(点 A,B,C,P 在同一平面内),求大楼的高度BC.(结果保留根号)
12.如图,l 是南北方向的海岸线,码头 A 与灯塔B 相距24千米,海岛C位于码头A 北偏东 方向.一艘勘测船从海岛 C 沿北偏西 方向往灯塔 B 行驶,沿线勘测石油资源,勘测发现位于码头A 北偏东 方向的 D 处石油资源丰富.若规划修建从 D 处到海岸线的输油管道,则输油管道的最短长度是多少千米 (结果保留根号)
13.如图,某数学兴趣小组为了测量古树 DE 的高度,采用了如下的方法:先从与古树底端 D 在同一水平线上的点A 出发,沿斜面坡度为 的斜坡AB前进 到达点 B,再沿水平方向继续前进一段距离后到达点 C.在点 C 处测得古树DE 的顶端E 的俯角为 37°,底部D的俯角为 60°,求古树 DE的高度.(参考数据: 计算结果用根号表示,不取近似值)
14.图1是某汽车的侧面示意图,折线段 ABC 表示车后盖,已知 1 m,BC=0.6 m ,∠ABC=123°,该车的高度 如图2,打开后备厢,车后盖 ABC落在 处,与水平面的夹角
(1)求打开后备厢后,车后盖最高点 到地面的距离;
(2)若小琳爸爸的身高为1.8m,他从打开的车后盖处经过,有没有碰头的危险 请说明理由.(结果精确到0.01m,参考数据:
易错点一 误认为三角函数值的一半等于半角的三角函数值
15. 在 Rt△ABC中, 求 的值.
小明给出了他自己的解答过程:
请问小明的解答过程是否正确 如果不正确,请写出正确的解答过程.
易错点二 不注意分类讨论,对问题考虑不全而漏解
16.在△ABC中, 求 BC的长.
解:如图,过点 A 作 AD⊥BC于点 D.
在 Rt△ABD 中, AB=4,
在 Rt△ACD中,
上述解法是否正确 如不正确,请给出正确的解法.
参考答案
1. A 2. D
或
解析:连接AE,EF,如图所示,
则 ∥
设每个小正方形的边长为a,
则
是直角三角形,
6. C
8.解:
9.解:(1)如图,作 于点E,
90°,
10.解:(1)如图,过点 A 作 BC边上的垂线,垂足为点 D.
在 Rt△ADC中,
由勾股定理,得 ∴BC=BD+CD=14;
(2)在 Rt△ABD中,
11.解:如图,过点 P 作PH⊥AB于点 H,过点 C 作 CQ⊥PH于点Q,而 CB⊥AB,
则四边形 CQHB 是矩形,
∴QH=BC,BH=CQ,
由题意,得AP=80米,∠PAH=60°,∠PCQ=30°,AB=70米,
(米),AH=AP·cos60°=40(米),
∴CQ=BH=70-40=30(米), (米),
(米),
所以,大楼的高度 BC为 米.
12.解:如图,过点 D 作DE⊥AB,垂足为点 E,
由题意,得∠BAD=15°,∠BAC = 60°,∠BCF =30°,AB∥FG,
∴∠ACG=∠BAC=60°,∠BCF=∠ABC=30°,∠CAD = ∠BAC -∠BAD=45°,
∴∠ACB=180°-∠ACG-∠BCF=90°,
∵AB=24千米,
(千米), (千米),CD=AC=12(千米),
千米,
在 Rt△BDE 中,∠ABC=30°, 千米,
所以,输油管道的最短长度是( 千米.
13.解:过点 B 作 于点F,
在 中,∴可设
解得 (负值已舍),
延长 BC,DE,相交于点 H,
∵BC是水平线,DE 是铅垂线,
和 都是直角三角形,
∵AD,BC都是水平线, ∴四边形 BFDH是矩形,
在 Rt△CDH中,
在 中,
所以,古树 DE的高度为
14.解:(1)如图,作. 垂足为点 E,
在 中,∵∠B'AD=27°,AB'=AB=1m,
∴B'E = AB'sin27°≈1×0.454=0.454 m,
∵平行线间的距离处处相等,
∴B'E+AO=0.454+1.7=2.154≈2.15 m,
所以,车后盖最高点 B到地面的距离为2.15 m;
(2)没有危险,理由:
如图,过C'作 垂足为点 F,
∵∠B'AD=27°,∠B'EA=90°,∴∠AB'E=63°,
∵∠AB'C'=∠ABC=123°, ∠AB'E=60°,
在 中, ∴.
∵平行线间的距离处处相等,∴C'到地面的距离为 2.15-0.3=1.85 m.
∵1.85>1.8,所以,没有危险.
15.解:小明的解答过程不正确,正确的解答过程:
在 Rt△ABC中,
∴∠A=60°,
16.解:不正确.正确解法:
①当△ABC为锐角三角形时,同题中解法;
②当△ABC 为钝角三角形时,
如图所示,过点 A 作 AD⊥BC交 BC 的延长线于点 D.
同①,得 BD=2,CD=1.∴BC=BD-CD=2-1= 1.
综上所述,BC的长为3 或1.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二章 直角三角形的边角关系
章末突破
类型一 锐角三角函数的定义
1.如图,在 Rt△ABC 中,∠ACB=90°,CD⊥AB于点 D,下列式子正确的是 ( )
2.已知 ,则锐角α的取值范围是 ( )
3.一等腰三角形的两边长分别为 4 cm 和6 cm,则其底角的余弦值为_________.
4.在 Rt△ABC 中,如果 AB=14,那么AC=_________.
5.在如图所示的正方形方格纸中,每个小的四边形都是相同的正方形,A,B,C,D都在格点处,AB 与CD 相交于点O,则 sin∠BOD的值为___________.
类型二 特殊角的三角函数值
6.已知在 中, 则的形状 ( )
A.一定是锐角三角形 B.一定是直角三角形 C.一定是钝角三角形 D.无法确定
7.若锐角 x满足则 x为___________.
8.计算:
类型三 解直角三角形
9.如图,在 中,.点 D 在 BC的延长线上,且 连接AD.
(1)求 BC的长;
(2)求 tanD.
10.如图,在 中,
(1)求 BC的长;
(2)求 tanB 的值.
类型四 三角函数的实际应用
11.无人机在实际生活中的应用越来越广泛.如图所示,某人利用无人机测量大楼的高度 BC,无人机在空中点 P 处,测得点 P 距地面上A 点 80米,点 A 处的俯角为 楼顶 C 点处的俯角为 已知点 A 与大楼的距离AB 为 70米(点 A,B,C,P 在同一平面内),求大楼的高度BC.(结果保留根号)
12.如图,l 是南北方向的海岸线,码头 A 与灯塔B 相距24千米,海岛C位于码头A 北偏东 方向.一艘勘测船从海岛 C 沿北偏西 方向往灯塔 B 行驶,沿线勘测石油资源,勘测发现位于码头A 北偏东 方向的 D 处石油资源丰富.若规划修建从 D 处到海岸线的输油管道,则输油管道的最短长度是多少千米 (结果保留根号)
13.如图,某数学兴趣小组为了测量古树 DE 的高度,采用了如下的方法:先从与古树底端 D 在同一水平线上的点A 出发,沿斜面坡度为 的斜坡AB前进 到达点 B,再沿水平方向继续前进一段距离后到达点 C.在点 C 处测得古树DE 的顶端E 的俯角为 37°,底部D的俯角为 60°,求古树 DE的高度.(参考数据: 计算结果用根号表示,不取近似值)
14.图1是某汽车的侧面示意图,折线段 ABC 表示车后盖,已知 1 m,BC=0.6 m ,∠ABC=123°,该车的高度 如图2,打开后备厢,车后盖 ABC落在 处,与水平面的夹角
(1)求打开后备厢后,车后盖最高点 到地面的距离;
(2)若小琳爸爸的身高为1.8m,他从打开的车后盖处经过,有没有碰头的危险 请说明理由.(结果精确到0.01m,参考数据:
易错点一 误认为三角函数值的一半等于半角的三角函数值
15. 在 Rt△ABC中, 求 的值.
小明给出了他自己的解答过程:
请问小明的解答过程是否正确 如果不正确,请写出正确的解答过程.
易错点二 不注意分类讨论,对问题考虑不全而漏解
16.在△ABC中, 求 BC的长.
解:如图,过点 A 作 AD⊥BC于点 D.
在 Rt△ABD 中, AB=4,
在 Rt△ACD中,
上述解法是否正确 如不正确,请给出正确的解法.
参考答案
1. A 2. D
或
解析:连接AE,EF,如图所示,
则 ∥
设每个小正方形的边长为a,
则
是直角三角形,
6. C
8.解:
9.解:(1)如图,作 于点E,
90°,
10.解:(1)如图,过点 A 作 BC边上的垂线,垂足为点 D.
在 Rt△ADC中,
由勾股定理,得 ∴BC=BD+CD=14;
(2)在 Rt△ABD中,
11.解:如图,过点 P 作PH⊥AB于点 H,过点 C 作 CQ⊥PH于点Q,而 CB⊥AB,
则四边形 CQHB 是矩形,
∴QH=BC,BH=CQ,
由题意,得AP=80米,∠PAH=60°,∠PCQ=30°,AB=70米,
(米),AH=AP·cos60°=40(米),
∴CQ=BH=70-40=30(米), (米),
(米),
所以,大楼的高度 BC为 米.
12.解:如图,过点 D 作DE⊥AB,垂足为点 E,
由题意,得∠BAD=15°,∠BAC = 60°,∠BCF =30°,AB∥FG,
∴∠ACG=∠BAC=60°,∠BCF=∠ABC=30°,∠CAD = ∠BAC -∠BAD=45°,
∴∠ACB=180°-∠ACG-∠BCF=90°,
∵AB=24千米,
(千米), (千米),CD=AC=12(千米),
千米,
在 Rt△BDE 中,∠ABC=30°, 千米,
所以,输油管道的最短长度是( 千米.
13.解:过点 B 作 于点F,
在 中,∴可设
解得 (负值已舍),
延长 BC,DE,相交于点 H,
∵BC是水平线,DE 是铅垂线,
和 都是直角三角形,
∵AD,BC都是水平线, ∴四边形 BFDH是矩形,
在 Rt△CDH中,
在 中,
所以,古树 DE的高度为
14.解:(1)如图,作. 垂足为点 E,
在 中,∵∠B'AD=27°,AB'=AB=1m,
∴B'E = AB'sin27°≈1×0.454=0.454 m,
∵平行线间的距离处处相等,
∴B'E+AO=0.454+1.7=2.154≈2.15 m,
所以,车后盖最高点 B到地面的距离为2.15 m;
(2)没有危险,理由:
如图,过C'作 垂足为点 F,
∵∠B'AD=27°,∠B'EA=90°,∴∠AB'E=63°,
∵∠AB'C'=∠ABC=123°, ∠AB'E=60°,
在 中, ∴.
∵平行线间的距离处处相等,∴C'到地面的距离为 2.15-0.3=1.85 m.
∵1.85>1.8,所以,没有危险.
15.解:小明的解答过程不正确,正确的解答过程:
在 Rt△ABC中,
∴∠A=60°,
16.解:不正确.正确解法:
①当△ABC为锐角三角形时,同题中解法;
②当△ABC 为钝角三角形时,
如图所示,过点 A 作 AD⊥BC交 BC 的延长线于点 D.
同①,得 BD=2,CD=1.∴BC=BD-CD=2-1= 1.
综上所述,BC的长为3 或1.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
