第二章 直角三角形的边角关系 专项训练 解直角三角形的实际应用的类型(含答案)
文档属性
| 名称 | 第二章 直角三角形的边角关系 专项训练 解直角三角形的实际应用的类型(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 15.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-31 05:38:39 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二章 直角三角形的边角关系
专项训练 解直角三角形的实际应用的类型
一 与坡度、坡角有关的应用
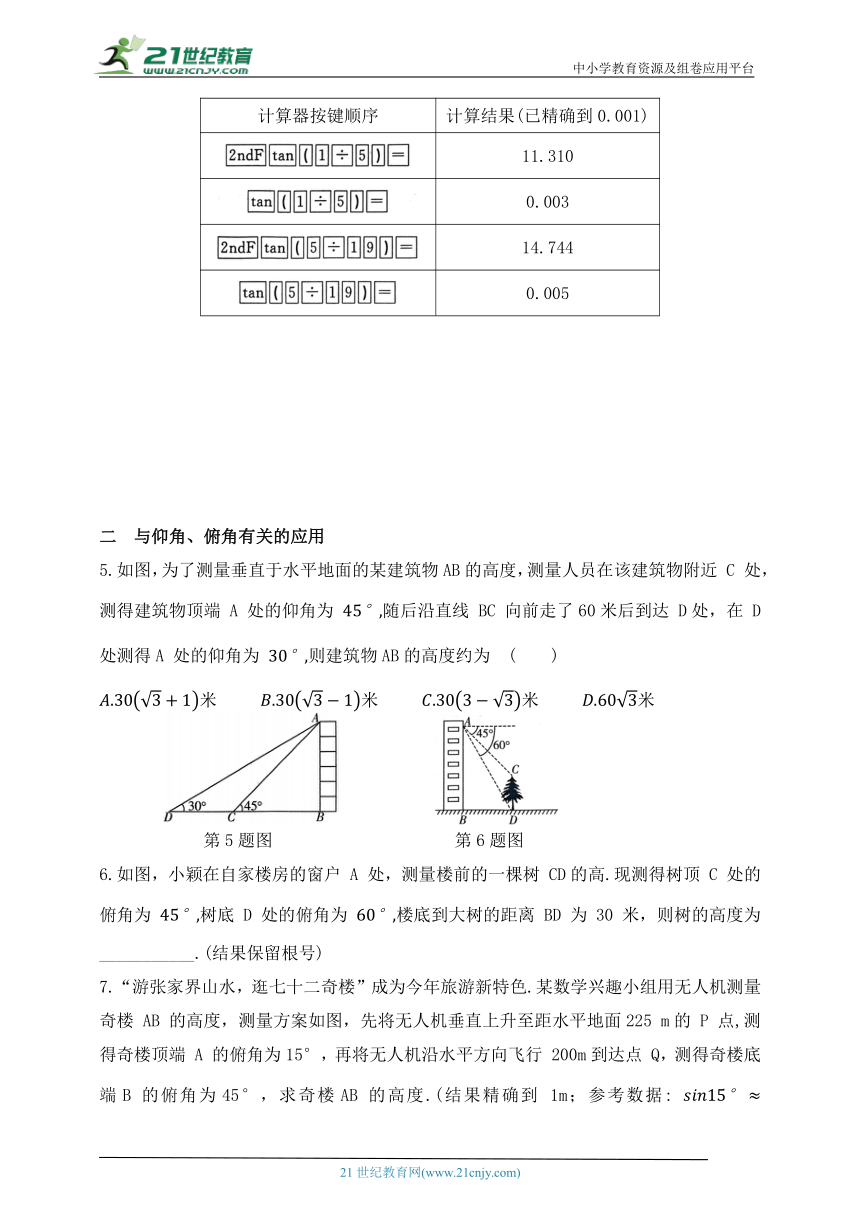
1.如图,某商场大厅自动扶梯AB 的坡度为i=1: 2.5, 过点 B 作BC⊥AC,垂足为点 C,若大厅水平距离 AC 的长为7.5m ,则两层之间的高度BC为( )
A.3 m B.4 m C.5 m D.6 m
第1题图 第2题图
2.如图,某地下停车库入口的设计示意图,已知 坡道 AB的坡比i=1: 2.4,AC的长为7.2 米,CD的长为0.4 米.按规定,车库坡道口上方需张贴限高标志,以便告知停车人车辆是否能安全驶入,根据所给数据,确定该车库入口的限高,即点 D到AB 的距离 DH 的值为____________米.
3.江边有一处高 10米, 背水坡角为45°的防洪大堤,大堤的横截面为梯形 ABCD,其中CD∥AB,∠DAB=45°(如图).某防洪指挥部发现该大堤急需加固,经调查论证,防洪指挥部专家组制定的加固方案是沿背水坡面 AD用土石进行加固,使上底加宽 3米,加固后背水坡 EF 的坡比为 则加固后坝底增加的宽度AF=___________米.
4.如图,某超市计划将门前的部分楼梯改造成无障碍通道.已知楼梯共有五级均匀分布的台阶,高 斜坡AC 的坡比为1:2,将要铺设的通道前方有一井盖,井盖边缘离楼梯底部的最短距离.为防止通道遮盖井盖,所铺设通道的坡角不得小于多少度 (结果精确到
参考数据表
计算器按键顺序 计算结果(已精确到0.001)
11.310
0.003
14.744
0.005
二 与仰角、俯角有关的应用
5.如图,为了测量垂直于水平地面的某建筑物AB的高度,测量人员在该建筑物附近 C 处,测得建筑物顶端 A 处的仰角为 随后沿直线 BC 向前走了60米后到达 D处,在 D 处测得A 处的仰角为 则建筑物AB的高度约为 ( )
米 米 米 米
第5题图 第6题图
6.如图,小颖在自家楼房的窗户 A 处,测量楼前的一棵树 CD的高.现测得树顶 C 处的俯角为 树底 D 处的俯角为 楼底到大树的距离 BD 为 30 米,则树的高度为___________.(结果保留根号)
7.“游张家界山水,逛七十二奇楼”成为今年旅游新特色.某数学兴趣小组用无人机测量奇楼 AB 的高度,测量方案如图,先将无人机垂直上升至距水平地面225 m的 P 点,测得奇楼顶端 A 的俯角为15°,再将无人机沿水平方向飞行 200m到达点 Q,测得奇楼底端B 的俯角为45°,求奇楼AB 的高度.(结果精确到 1m;参考数据: 0.27)
8.如图,一人在道路上骑行,BD段是坡路,其余为平路,当他路过A,B 两点时,一架无人机从空中的C点处测得A,B两点的俯角分别为 和 点A,B,C,D,E,F 在同一平面内,CE 是无人机到平路DF 的距离,求 CE 的长.(结果精确到整数;参考数据:
三 与方向角有关的应用
9.一艘轮船位于灯塔 P 的南偏东 方向,距离灯塔 30海里的A 处,它沿北偏东 方向航行一段时间后,到达位于灯塔 P 的北偏东( 方向上的 B 处,此时轮船与灯塔 P 的距离约为__________海里.(参考数据:
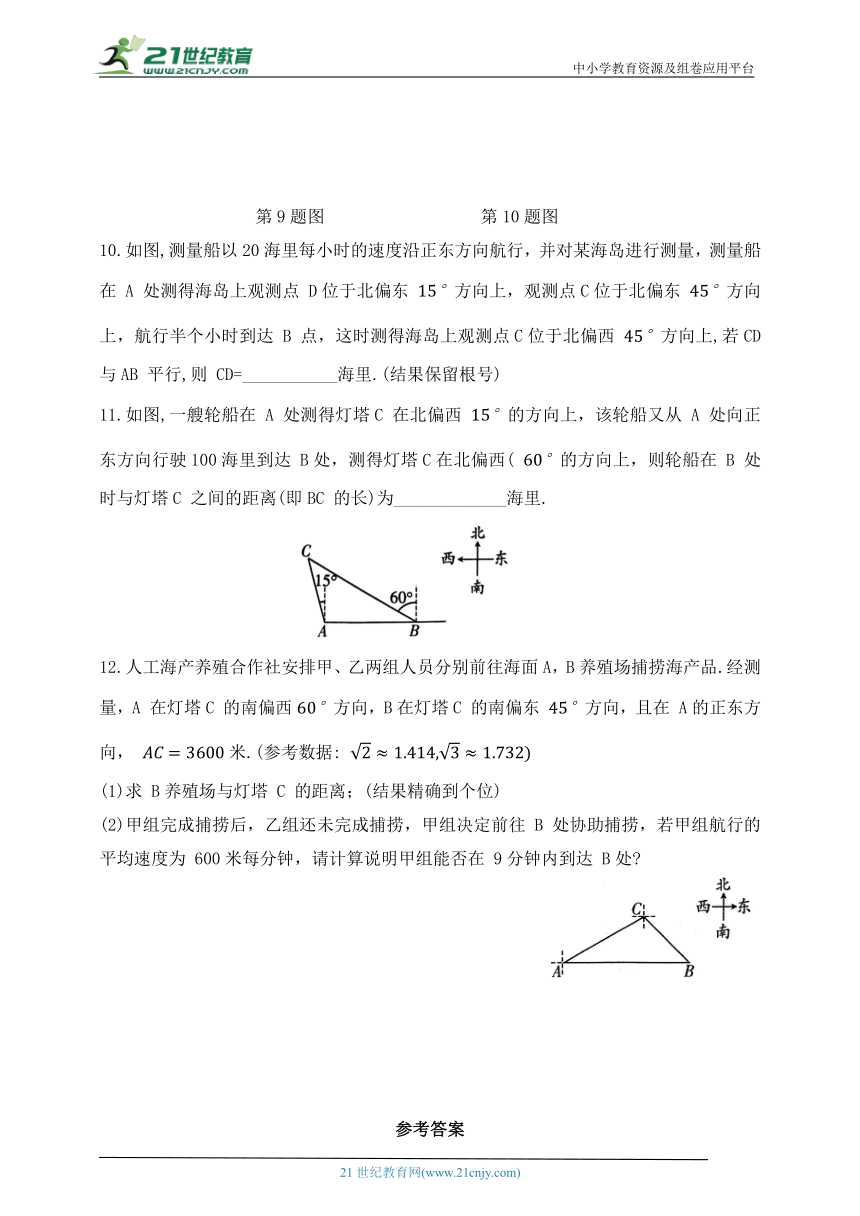
第9题图 第10题图
10.如图,测量船以20海里每小时的速度沿正东方向航行,并对某海岛进行测量,测量船在 A 处测得海岛上观测点 D位于北偏东 方向上,观测点C位于北偏东 方向上,航行半个小时到达 B 点,这时测得海岛上观测点C位于北偏西 方向上,若CD与AB 平行,则 CD=___________海里.(结果保留根号)
11.如图,一艘轮船在 A 处测得灯塔C 在北偏西 的方向上,该轮船又从 A 处向正东方向行驶100海里到达 B处,测得灯塔C在北偏西( 的方向上,则轮船在 B 处时与灯塔C 之间的距离(即BC 的长)为_____________海里.
12.人工海产养殖合作社安排甲、乙两组人员分别前往海面A,B养殖场捕捞海产品.经测量,A 在灯塔C 的南偏西方向,B在灯塔C 的南偏东 方向,且在 A的正东方向, 米.(参考数据:
(1)求 B养殖场与灯塔 C 的距离;(结果精确到个位)
(2)甲组完成捕捞后,乙组还未完成捕捞,甲组决定前往 B 处协助捕捞,若甲组航行的平均速度为 600米每分钟,请计算说明甲组能否在 9分钟内到达 B处
参考答案
1. A
4.解:如图,
由题意,得 (米),
∵斜坡AC的坡比为1: 2,
(米), (米),
米, 3.75(米),
在 中,
查表,得.
所以,为防止通道遮盖井盖,所铺设通道的坡角不得小于 12度.
5. A
米
7.解:如图,延长 BA,交 PQ的延长线于点C,
则 由题意,得
在 中,
在 中,
110(m),
所以,奇楼AB的高度约为 110m.
8.解:如图,延长 AB,交 CE 于点 H,过点 B 作BG⊥DF,垂足为点G,
由题意,得 BG=HE,CM∥AH,
∴ ∠CAH =∠MCA = 30°,∠CBH=∠MCB=45°,
设 BH=xm,
∵AB=40 m,∴AH=AB+BH=(x+40)m,
在 Rt△ACH中, 40)m,
在 Rt△CBH中,CH=BH·tan45°=x(m),
解得
∵∠BDF=159°,∴∠BDG=180°-∠BDF=21°,
在 Rt△BDG中,BD=20 m,
∴BG=BD·sin21°≈20×0.36=7.2(m),∴BG=EH=7.2m,
62(m),
所以,CE 的长约为 62 m.
9. 50
解析:如图,过点 D 作 DE⊥AB,垂足为点 E.
由题意,得 AB= 20× 海里,
∠FAD=15°, ∠FAC = 45°, ∠FAB=90°,∠CBA=90°-45°=45°,
∴∠DAC=∠FAC-∠FAD=30°,∠CAB=∠FAB-∠FAC=45°,
∴∠ACB=180°-∠CAB-∠CBA=90°.
在 Rt△ACB 中,
设 DE=x海里,
在 Rt△DAE中, (海里),
∵DC∥AB,∴∠DCA=∠CAB=45°.
在 Rt△DEC中, (海里), (海里).
∵AE+EC=AC,
海里.
12.解:(1)过点 C 作 CD⊥AB 于点 D,
在 Rt△ACD中,∠ACD=60°,AC=3 600米,
(米),
(米).
在 Rt△BCD中,∠BCD=45°,∴∠B=45°=∠BCD,∴BD=CD=1800(米),
1.414≈2545(米).
所以,B 养殖场与灯塔 C 的距离约为2545米;
1.732+1800≈4 917.6(米),
600×9=5 400(米),
∵5 400米>4 917.6米,∴能在 9分钟内到达 B 处.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二章 直角三角形的边角关系
专项训练 解直角三角形的实际应用的类型
一 与坡度、坡角有关的应用
1.如图,某商场大厅自动扶梯AB 的坡度为i=1: 2.5, 过点 B 作BC⊥AC,垂足为点 C,若大厅水平距离 AC 的长为7.5m ,则两层之间的高度BC为( )
A.3 m B.4 m C.5 m D.6 m
第1题图 第2题图
2.如图,某地下停车库入口的设计示意图,已知 坡道 AB的坡比i=1: 2.4,AC的长为7.2 米,CD的长为0.4 米.按规定,车库坡道口上方需张贴限高标志,以便告知停车人车辆是否能安全驶入,根据所给数据,确定该车库入口的限高,即点 D到AB 的距离 DH 的值为____________米.
3.江边有一处高 10米, 背水坡角为45°的防洪大堤,大堤的横截面为梯形 ABCD,其中CD∥AB,∠DAB=45°(如图).某防洪指挥部发现该大堤急需加固,经调查论证,防洪指挥部专家组制定的加固方案是沿背水坡面 AD用土石进行加固,使上底加宽 3米,加固后背水坡 EF 的坡比为 则加固后坝底增加的宽度AF=___________米.
4.如图,某超市计划将门前的部分楼梯改造成无障碍通道.已知楼梯共有五级均匀分布的台阶,高 斜坡AC 的坡比为1:2,将要铺设的通道前方有一井盖,井盖边缘离楼梯底部的最短距离.为防止通道遮盖井盖,所铺设通道的坡角不得小于多少度 (结果精确到
参考数据表
计算器按键顺序 计算结果(已精确到0.001)
11.310
0.003
14.744
0.005
二 与仰角、俯角有关的应用
5.如图,为了测量垂直于水平地面的某建筑物AB的高度,测量人员在该建筑物附近 C 处,测得建筑物顶端 A 处的仰角为 随后沿直线 BC 向前走了60米后到达 D处,在 D 处测得A 处的仰角为 则建筑物AB的高度约为 ( )
米 米 米 米
第5题图 第6题图
6.如图,小颖在自家楼房的窗户 A 处,测量楼前的一棵树 CD的高.现测得树顶 C 处的俯角为 树底 D 处的俯角为 楼底到大树的距离 BD 为 30 米,则树的高度为___________.(结果保留根号)
7.“游张家界山水,逛七十二奇楼”成为今年旅游新特色.某数学兴趣小组用无人机测量奇楼 AB 的高度,测量方案如图,先将无人机垂直上升至距水平地面225 m的 P 点,测得奇楼顶端 A 的俯角为15°,再将无人机沿水平方向飞行 200m到达点 Q,测得奇楼底端B 的俯角为45°,求奇楼AB 的高度.(结果精确到 1m;参考数据: 0.27)
8.如图,一人在道路上骑行,BD段是坡路,其余为平路,当他路过A,B 两点时,一架无人机从空中的C点处测得A,B两点的俯角分别为 和 点A,B,C,D,E,F 在同一平面内,CE 是无人机到平路DF 的距离,求 CE 的长.(结果精确到整数;参考数据:
三 与方向角有关的应用
9.一艘轮船位于灯塔 P 的南偏东 方向,距离灯塔 30海里的A 处,它沿北偏东 方向航行一段时间后,到达位于灯塔 P 的北偏东( 方向上的 B 处,此时轮船与灯塔 P 的距离约为__________海里.(参考数据:
第9题图 第10题图
10.如图,测量船以20海里每小时的速度沿正东方向航行,并对某海岛进行测量,测量船在 A 处测得海岛上观测点 D位于北偏东 方向上,观测点C位于北偏东 方向上,航行半个小时到达 B 点,这时测得海岛上观测点C位于北偏西 方向上,若CD与AB 平行,则 CD=___________海里.(结果保留根号)
11.如图,一艘轮船在 A 处测得灯塔C 在北偏西 的方向上,该轮船又从 A 处向正东方向行驶100海里到达 B处,测得灯塔C在北偏西( 的方向上,则轮船在 B 处时与灯塔C 之间的距离(即BC 的长)为_____________海里.
12.人工海产养殖合作社安排甲、乙两组人员分别前往海面A,B养殖场捕捞海产品.经测量,A 在灯塔C 的南偏西方向,B在灯塔C 的南偏东 方向,且在 A的正东方向, 米.(参考数据:
(1)求 B养殖场与灯塔 C 的距离;(结果精确到个位)
(2)甲组完成捕捞后,乙组还未完成捕捞,甲组决定前往 B 处协助捕捞,若甲组航行的平均速度为 600米每分钟,请计算说明甲组能否在 9分钟内到达 B处
参考答案
1. A
4.解:如图,
由题意,得 (米),
∵斜坡AC的坡比为1: 2,
(米), (米),
米, 3.75(米),
在 中,
查表,得.
所以,为防止通道遮盖井盖,所铺设通道的坡角不得小于 12度.
5. A
米
7.解:如图,延长 BA,交 PQ的延长线于点C,
则 由题意,得
在 中,
在 中,
110(m),
所以,奇楼AB的高度约为 110m.
8.解:如图,延长 AB,交 CE 于点 H,过点 B 作BG⊥DF,垂足为点G,
由题意,得 BG=HE,CM∥AH,
∴ ∠CAH =∠MCA = 30°,∠CBH=∠MCB=45°,
设 BH=xm,
∵AB=40 m,∴AH=AB+BH=(x+40)m,
在 Rt△ACH中, 40)m,
在 Rt△CBH中,CH=BH·tan45°=x(m),
解得
∵∠BDF=159°,∴∠BDG=180°-∠BDF=21°,
在 Rt△BDG中,BD=20 m,
∴BG=BD·sin21°≈20×0.36=7.2(m),∴BG=EH=7.2m,
62(m),
所以,CE 的长约为 62 m.
9. 50
解析:如图,过点 D 作 DE⊥AB,垂足为点 E.
由题意,得 AB= 20× 海里,
∠FAD=15°, ∠FAC = 45°, ∠FAB=90°,∠CBA=90°-45°=45°,
∴∠DAC=∠FAC-∠FAD=30°,∠CAB=∠FAB-∠FAC=45°,
∴∠ACB=180°-∠CAB-∠CBA=90°.
在 Rt△ACB 中,
设 DE=x海里,
在 Rt△DAE中, (海里),
∵DC∥AB,∴∠DCA=∠CAB=45°.
在 Rt△DEC中, (海里), (海里).
∵AE+EC=AC,
海里.
12.解:(1)过点 C 作 CD⊥AB 于点 D,
在 Rt△ACD中,∠ACD=60°,AC=3 600米,
(米),
(米).
在 Rt△BCD中,∠BCD=45°,∴∠B=45°=∠BCD,∴BD=CD=1800(米),
1.414≈2545(米).
所以,B 养殖场与灯塔 C 的距离约为2545米;
1.732+1800≈4 917.6(米),
600×9=5 400(米),
∵5 400米>4 917.6米,∴能在 9分钟内到达 B 处.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
