第二章 直角三角形的边角关系 综合测试题(含答案)
文档属性
| 名称 | 第二章 直角三角形的边角关系 综合测试题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 15.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-31 05:38:12 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第二章综合测试题
时间: 90分钟 满分: 120分 得 分:__________
一、选择题(每题3分,共30分)
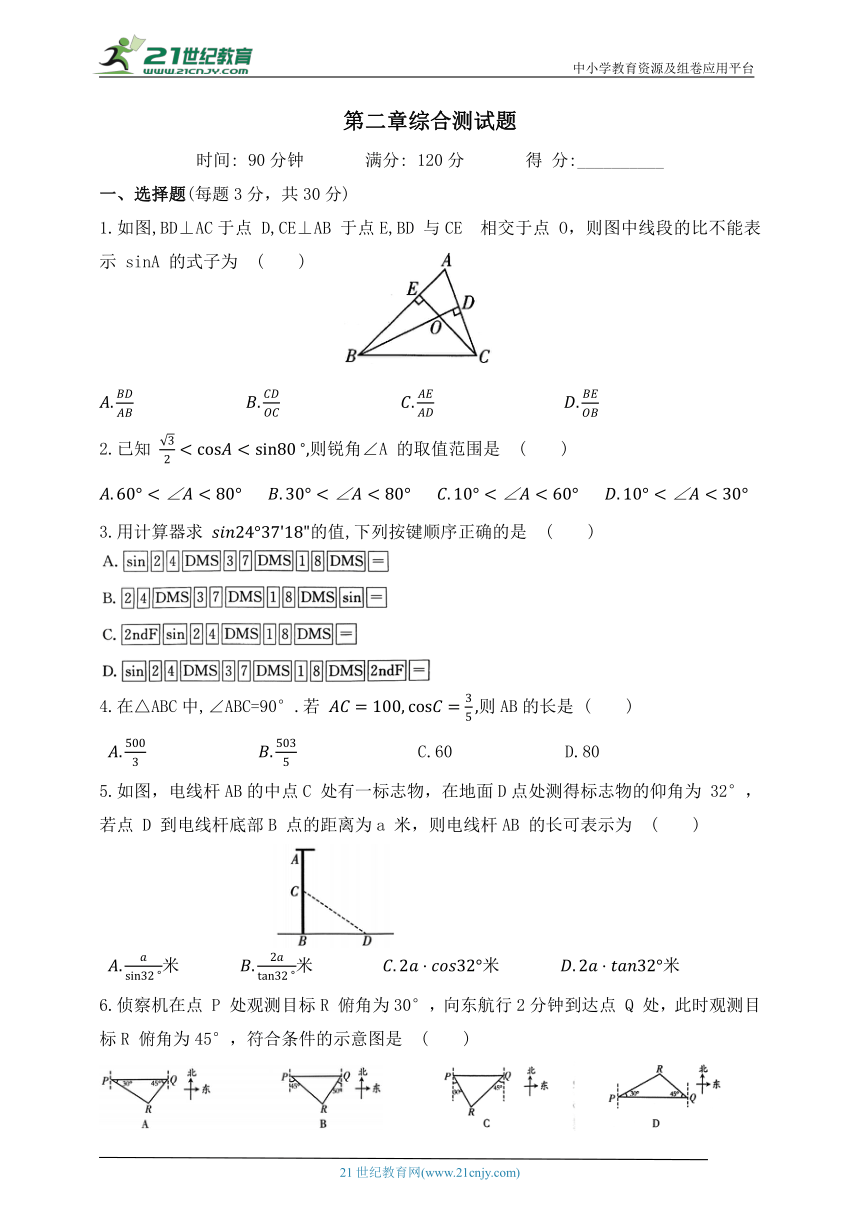
1.如图,BD⊥AC于点 D,CE⊥AB 于点E,BD 与CE 相交于点 O,则图中线段的比不能表示 sinA 的式子为 ( )
2.已知 则锐角∠A 的取值范围是 ( )
3.用计算器求 的值,下列按键顺序正确的是 ( )
4.在△ABC中,∠ABC=90°.若 则AB的长是 ( )
C.60 D.80
5.如图,电线杆AB的中点C 处有一标志物,在地面D点处测得标志物的仰角为 32°,若点 D 到电线杆底部B 点的距离为a 米,则电线杆AB 的长可表示为 ( )
米 米 米 米
6.侦察机在点 P 处观测目标R 俯角为30°,向东航行2分钟到达点 Q 处,此时观测目标R 俯角为45°,符合条件的示意图是 ( )
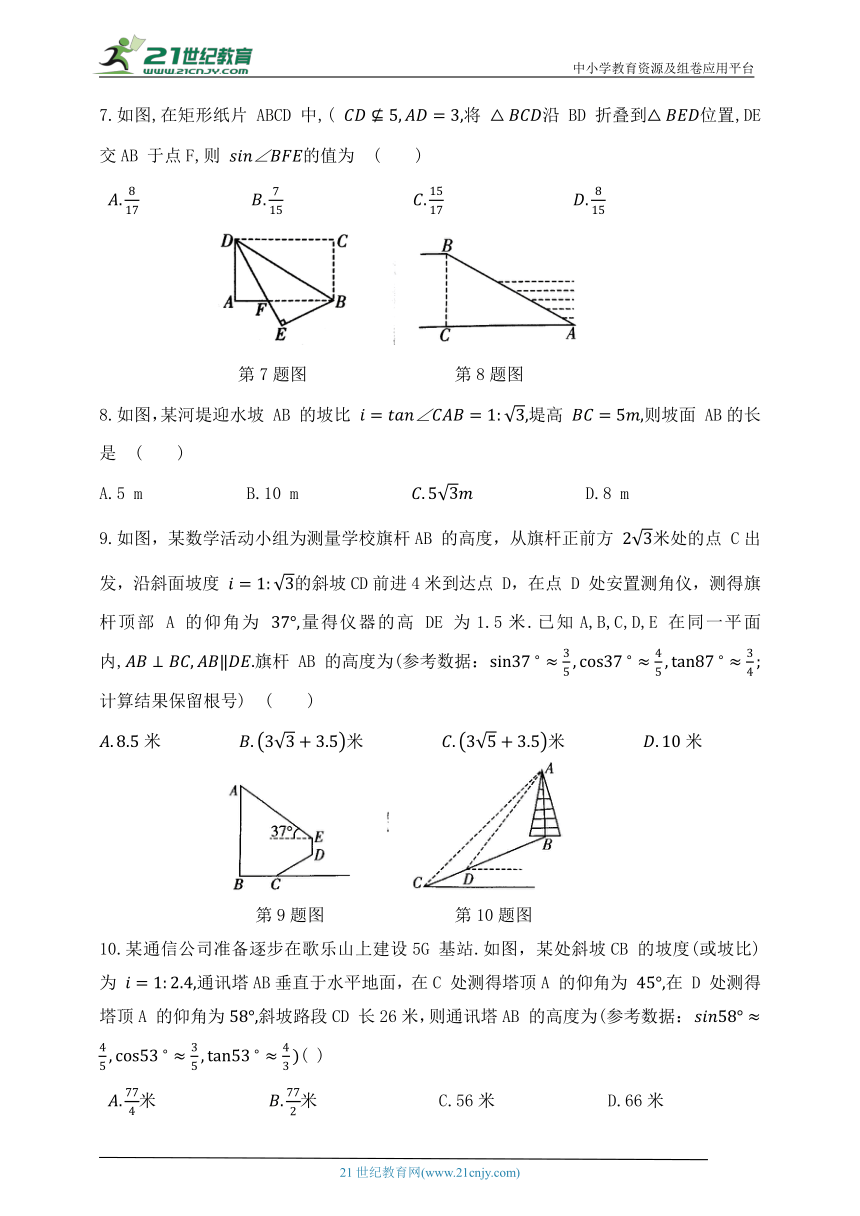
7.如图,在矩形纸片 ABCD 中,( 将 沿 BD 折叠到位置,DE 交AB 于点F,则 的值为 ( )
第7题图 第8题图
8.如图,某河堤迎水坡 AB 的坡比 堤高 则坡面 AB的长是 ( )
A.5 m B.10 m D.8 m
9.如图,某数学活动小组为测量学校旗杆AB 的高度,从旗杆正前方 米处的点 C出发,沿斜面坡度 的斜坡CD前进4米到达点 D,在点 D 处安置测角仪,测得旗杆顶部 A 的仰角为 量得仪器的高 DE 为1.5米.已知A,B,C,D,E 在同一平面内,旗杆 AB 的高度为(参考数据: 计算结果保留根号) ( )
米 米 米
第9题图 第10题图
10.某通信公司准备逐步在歌乐山上建设5G 基站.如图,某处斜坡CB 的坡度(或坡比)为 通讯塔AB垂直于水平地面,在C 处测得塔顶A 的仰角为 在 D 处测得塔顶A 的仰角为斜坡路段CD 长26米,则通讯塔AB 的高度为(参考数据: ( )
米 米 C.56米 D.66米
二、填空题(每题3分,共18分)
11.已知a是锐角, 则 sina的值为__________;
12.已知CD是 斜边上的高线,且 若则
第12题图 第13题图
13.在正方形网格中, 如图放置,则 的值为___________.
14.如图,将 的 按如图所示的方式放置在一把刻度尺上,顶点 O与尺下沿的端点重合,OA 与尺下沿重合,OB与尺上沿的交点 B 在尺上的读数为2cm,若按相同的方式将 的 放置在该刻度尺上,则 OC与尺上沿的交点C 在尺上的读数是___________cm.(结果精确到0.1cm;参考数据
15.如图,一艘海轮位于灯塔 P 的北偏东 方向,距离灯塔100海里的A 处,它沿正南方向以 海里/小时的速度航行t小时后,到达位于灯塔 P的南偏东 方向上的点 B 处,则 __________小时.
第15题图 第16题图
16.如图,已知在 中, 边 AC的长为_________.
三、解答题(共72分)
17.(10分)
(1)计算: .
(2)计算:
18.(10分)如图,在. 中, BF 交 AD 于点 E.求:
(1)AD的长;
(2)tan∠FBC的值.
19.(12分)为了丰富学生的文化生活,学校利用假期组织学生到素质教育基地A 和科技智能馆B 参观学习,学生从学校出发,走到C处时,发现 A位于C 的北偏西 25°方向上,B位于C 的北偏西方向上,老师将学生分成甲乙两组,甲组前往A 地,乙组前往 B 地,已知B 在A 的南偏西20°方向上,且相距1000米,请求出甲组同学比乙组同学大约多走多远的路程.(参考数据:
20.(12分)风电项目对于调整能源结构和转变经济发展方式具有重要意义.某电力部门在一处坡角为: 的坡地新安装了一架风力发电机,如图1.某校实践活动小组对该坡地上的这架风力发电机的塔杆高度进行了测量,图2为测量示意图.已知斜坡CD长16米,在地面点 A 处测得风力发电机塔杆顶端P 点的仰角为 利用无人机在点A 的正上方53米的点 B 处测得 P 点的俯角为 求该风力发电机塔杆 PD 的高度.(参考数据: 0.325)
21.(14分)为了增强学生体质、锤炼学生意志,某校组织了一次定向越野拉练活动.如图,A 点为出发点,途中设置两个检查点,分别为 B点和C 点,行进路线为A→B→C→A. B 点在A 点的南偏东 方向 处,C点在A 点的北偏东80°方向,行进路线AB 和BC所在直线的夹角∠ABC为45°.
(1)求行进路线 BC 和CA 所在直线的夹角∠BCA 的度数;
(2)求检查点 B 和C 之间的距离.(结果保留根号)
22.(14分)随着科技的发展,无人机已被广泛应用于生产和生活,如代替人们在高空测量距离和角度.某校“综合与实践”活动小组的同学要测量AB,CD两座楼之间的距离,他们借助无人机设计了如下测量方案:无人机在AB,CD两楼之间上方的点O 处,点O距地面AC的高度为120m,此时观测到楼AB 底部点A 处的俯角为 楼 CD 上点 E 处的俯角为 沿水平方向由点 O 飞行48 m到达点 F,测得点 E 处俯角为( 其中点 A,B,C,D,E,F,O均在同一竖直平面内.楼AB 与CD 之间的距离AC 的长为多少米 (结果精确到1m;参考数据:
参考答案
1. C 2. D 3. A 4. D 5. D 6. A 7. C 8. B 9. B
10. B 解析:如图,延长AB,与水平线交于点 F, 过点 D作 点 M为垂足,过点 D 作点 E 为垂足,
∵斜坡 CB 的坡度为
设 米,则 米,
在 中, 米,由勾股定理,得
即 解得k=2,∴DM=10(米),CM=24(米),
∵斜坡 CB的坡度为i=1: 2.4,
设 DE=12a米,则 BE=5a米,
∵∠ACF=45°,∴AF=CF=CM+MF=CM+DE=(24+12a)米,
∴AE=AF-EF=24+12a-10=(14+12a)米,
在 Rt△ADE 中,DE=12a 米,AE=(14+12a)米,
解得
∴DE=12a=42(米),AE=14+12a=56(米),(米),
(米),
所以,基站塔AB的高为 米.
14.2.7
17.解:(1)原式
(2)原式
18.解:(1)∵AD⊥BC,
(2)∵AD⊥BC,
由(1),得
由勾 股 定 理,得
是等腰直角三角形,
∴∠BFC=90°,∴∠FBC=45°,
∴tan∠FBC=tan45°=1.
19.解:如图,过点 B 作BE⊥AC,垂足为点 E,
由题意,得∠ACD = 25°,∠BCD = 55°,∠FAB =20°,AB=1 000米,CD∥FA,
∴ ∠ACB = ∠BCD -∠ACD = 30°, ∠CAF=∠ACD=25°,
∴∠BAC=∠FAB+∠CAF=45°,
在 Rt△ABE中,AE=AB·cos45°=1 000× (米),
(米),
在 Rt△BCE中,∠BCE=30°,
(米), (米),
米,
500 -500 ≈520( (米),
所以,甲组同学比乙组同学大约多走 520 米的路程.
20.解:延长PD 交AC 于点F,延长DP 交BE 于点G,
由题意,得 PF⊥AF,DG⊥BE,AB = FG = 53 米, AF=BG,
设AF=BG=x米,
在 Rt△CDF 中,∠DCF=30°,CD=16米,(米),
在 Rt△PAF中,∠PAF=45°,∴PF=AF·tan45°=x(米),
在 Rt△BPG中,∠GBP=18°,∴GP=BG·tan18°≈0.325x(米),
∴FG=PF+PG=x+0.325x=1.325x(米),
∴1.325x=53,解得x=40,∴PF=40米,
∴PD=PF-DF=40-8=32(米),
所以,该风力发电机塔杆 PD 的高度约为32米.
21.解:(1)由题意,得∠NAC=80°,∠BAS=25°,
∴∠CAB=180°-∠NAC-∠BAS=75°,
∵∠ABC=45°,∴∠ACB=180°-∠CAB-∠ABC=60°,
∴行进路线 BC 和 CA 所在直线 的夹 角∠BCA 的度数为 60°;
(2)过点 A 作AD⊥BC,垂足为点 D,
在 Rt△ABD中,AB=
∴AD=AB·sin45°=BD=AB·cos45°=
在 Rt△ADC 中,∠ACB=60°,
所以,检查点 B 和C 之间的距离
22.解:延长AB交OF 于点G,延长CD交OF 于点 H,
由题意,得 AG⊥OF,CH⊥OF,AG=120 m, OF=48m,AC=GH,
∵∠HFE 是△OFE 的一个外角,∠HFE =60°,∠FOE=30°,
∴∠OEF=∠HFE-∠FOE=30°,∴∠FOE=∠OEF=30°,∴OF=EF=48 m,
在 Rt△HFE中, 24(m),
在 Rt△AGO中,∠AOG=70°,
24≈116(m),
所以,楼 AB 与CD 之间的距离AC 的长约为116 m.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二章综合测试题
时间: 90分钟 满分: 120分 得 分:__________
一、选择题(每题3分,共30分)
1.如图,BD⊥AC于点 D,CE⊥AB 于点E,BD 与CE 相交于点 O,则图中线段的比不能表示 sinA 的式子为 ( )
2.已知 则锐角∠A 的取值范围是 ( )
3.用计算器求 的值,下列按键顺序正确的是 ( )
4.在△ABC中,∠ABC=90°.若 则AB的长是 ( )
C.60 D.80
5.如图,电线杆AB的中点C 处有一标志物,在地面D点处测得标志物的仰角为 32°,若点 D 到电线杆底部B 点的距离为a 米,则电线杆AB 的长可表示为 ( )
米 米 米 米
6.侦察机在点 P 处观测目标R 俯角为30°,向东航行2分钟到达点 Q 处,此时观测目标R 俯角为45°,符合条件的示意图是 ( )
7.如图,在矩形纸片 ABCD 中,( 将 沿 BD 折叠到位置,DE 交AB 于点F,则 的值为 ( )
第7题图 第8题图
8.如图,某河堤迎水坡 AB 的坡比 堤高 则坡面 AB的长是 ( )
A.5 m B.10 m D.8 m
9.如图,某数学活动小组为测量学校旗杆AB 的高度,从旗杆正前方 米处的点 C出发,沿斜面坡度 的斜坡CD前进4米到达点 D,在点 D 处安置测角仪,测得旗杆顶部 A 的仰角为 量得仪器的高 DE 为1.5米.已知A,B,C,D,E 在同一平面内,旗杆 AB 的高度为(参考数据: 计算结果保留根号) ( )
米 米 米
第9题图 第10题图
10.某通信公司准备逐步在歌乐山上建设5G 基站.如图,某处斜坡CB 的坡度(或坡比)为 通讯塔AB垂直于水平地面,在C 处测得塔顶A 的仰角为 在 D 处测得塔顶A 的仰角为斜坡路段CD 长26米,则通讯塔AB 的高度为(参考数据: ( )
米 米 C.56米 D.66米
二、填空题(每题3分,共18分)
11.已知a是锐角, 则 sina的值为__________;
12.已知CD是 斜边上的高线,且 若则
第12题图 第13题图
13.在正方形网格中, 如图放置,则 的值为___________.
14.如图,将 的 按如图所示的方式放置在一把刻度尺上,顶点 O与尺下沿的端点重合,OA 与尺下沿重合,OB与尺上沿的交点 B 在尺上的读数为2cm,若按相同的方式将 的 放置在该刻度尺上,则 OC与尺上沿的交点C 在尺上的读数是___________cm.(结果精确到0.1cm;参考数据
15.如图,一艘海轮位于灯塔 P 的北偏东 方向,距离灯塔100海里的A 处,它沿正南方向以 海里/小时的速度航行t小时后,到达位于灯塔 P的南偏东 方向上的点 B 处,则 __________小时.
第15题图 第16题图
16.如图,已知在 中, 边 AC的长为_________.
三、解答题(共72分)
17.(10分)
(1)计算: .
(2)计算:
18.(10分)如图,在. 中, BF 交 AD 于点 E.求:
(1)AD的长;
(2)tan∠FBC的值.
19.(12分)为了丰富学生的文化生活,学校利用假期组织学生到素质教育基地A 和科技智能馆B 参观学习,学生从学校出发,走到C处时,发现 A位于C 的北偏西 25°方向上,B位于C 的北偏西方向上,老师将学生分成甲乙两组,甲组前往A 地,乙组前往 B 地,已知B 在A 的南偏西20°方向上,且相距1000米,请求出甲组同学比乙组同学大约多走多远的路程.(参考数据:
20.(12分)风电项目对于调整能源结构和转变经济发展方式具有重要意义.某电力部门在一处坡角为: 的坡地新安装了一架风力发电机,如图1.某校实践活动小组对该坡地上的这架风力发电机的塔杆高度进行了测量,图2为测量示意图.已知斜坡CD长16米,在地面点 A 处测得风力发电机塔杆顶端P 点的仰角为 利用无人机在点A 的正上方53米的点 B 处测得 P 点的俯角为 求该风力发电机塔杆 PD 的高度.(参考数据: 0.325)
21.(14分)为了增强学生体质、锤炼学生意志,某校组织了一次定向越野拉练活动.如图,A 点为出发点,途中设置两个检查点,分别为 B点和C 点,行进路线为A→B→C→A. B 点在A 点的南偏东 方向 处,C点在A 点的北偏东80°方向,行进路线AB 和BC所在直线的夹角∠ABC为45°.
(1)求行进路线 BC 和CA 所在直线的夹角∠BCA 的度数;
(2)求检查点 B 和C 之间的距离.(结果保留根号)
22.(14分)随着科技的发展,无人机已被广泛应用于生产和生活,如代替人们在高空测量距离和角度.某校“综合与实践”活动小组的同学要测量AB,CD两座楼之间的距离,他们借助无人机设计了如下测量方案:无人机在AB,CD两楼之间上方的点O 处,点O距地面AC的高度为120m,此时观测到楼AB 底部点A 处的俯角为 楼 CD 上点 E 处的俯角为 沿水平方向由点 O 飞行48 m到达点 F,测得点 E 处俯角为( 其中点 A,B,C,D,E,F,O均在同一竖直平面内.楼AB 与CD 之间的距离AC 的长为多少米 (结果精确到1m;参考数据:
参考答案
1. C 2. D 3. A 4. D 5. D 6. A 7. C 8. B 9. B
10. B 解析:如图,延长AB,与水平线交于点 F, 过点 D作 点 M为垂足,过点 D 作点 E 为垂足,
∵斜坡 CB 的坡度为
设 米,则 米,
在 中, 米,由勾股定理,得
即 解得k=2,∴DM=10(米),CM=24(米),
∵斜坡 CB的坡度为i=1: 2.4,
设 DE=12a米,则 BE=5a米,
∵∠ACF=45°,∴AF=CF=CM+MF=CM+DE=(24+12a)米,
∴AE=AF-EF=24+12a-10=(14+12a)米,
在 Rt△ADE 中,DE=12a 米,AE=(14+12a)米,
解得
∴DE=12a=42(米),AE=14+12a=56(米),(米),
(米),
所以,基站塔AB的高为 米.
14.2.7
17.解:(1)原式
(2)原式
18.解:(1)∵AD⊥BC,
(2)∵AD⊥BC,
由(1),得
由勾 股 定 理,得
是等腰直角三角形,
∴∠BFC=90°,∴∠FBC=45°,
∴tan∠FBC=tan45°=1.
19.解:如图,过点 B 作BE⊥AC,垂足为点 E,
由题意,得∠ACD = 25°,∠BCD = 55°,∠FAB =20°,AB=1 000米,CD∥FA,
∴ ∠ACB = ∠BCD -∠ACD = 30°, ∠CAF=∠ACD=25°,
∴∠BAC=∠FAB+∠CAF=45°,
在 Rt△ABE中,AE=AB·cos45°=1 000× (米),
(米),
在 Rt△BCE中,∠BCE=30°,
(米), (米),
米,
500 -500 ≈520( (米),
所以,甲组同学比乙组同学大约多走 520 米的路程.
20.解:延长PD 交AC 于点F,延长DP 交BE 于点G,
由题意,得 PF⊥AF,DG⊥BE,AB = FG = 53 米, AF=BG,
设AF=BG=x米,
在 Rt△CDF 中,∠DCF=30°,CD=16米,(米),
在 Rt△PAF中,∠PAF=45°,∴PF=AF·tan45°=x(米),
在 Rt△BPG中,∠GBP=18°,∴GP=BG·tan18°≈0.325x(米),
∴FG=PF+PG=x+0.325x=1.325x(米),
∴1.325x=53,解得x=40,∴PF=40米,
∴PD=PF-DF=40-8=32(米),
所以,该风力发电机塔杆 PD 的高度约为32米.
21.解:(1)由题意,得∠NAC=80°,∠BAS=25°,
∴∠CAB=180°-∠NAC-∠BAS=75°,
∵∠ABC=45°,∴∠ACB=180°-∠CAB-∠ABC=60°,
∴行进路线 BC 和 CA 所在直线 的夹 角∠BCA 的度数为 60°;
(2)过点 A 作AD⊥BC,垂足为点 D,
在 Rt△ABD中,AB=
∴AD=AB·sin45°=BD=AB·cos45°=
在 Rt△ADC 中,∠ACB=60°,
所以,检查点 B 和C 之间的距离
22.解:延长AB交OF 于点G,延长CD交OF 于点 H,
由题意,得 AG⊥OF,CH⊥OF,AG=120 m, OF=48m,AC=GH,
∵∠HFE 是△OFE 的一个外角,∠HFE =60°,∠FOE=30°,
∴∠OEF=∠HFE-∠FOE=30°,∴∠FOE=∠OEF=30°,∴OF=EF=48 m,
在 Rt△HFE中, 24(m),
在 Rt△AGO中,∠AOG=70°,
24≈116(m),
所以,楼 AB 与CD 之间的距离AC 的长约为116 m.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
