北师大版数学九年级上册 第4章 图形的相似测试卷(含答案)
文档属性
| 名称 | 北师大版数学九年级上册 第4章 图形的相似测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 854.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-31 15:03:54 | ||
图片预览


文档简介
第4章测试卷
(满分120分,时间120分钟)
题号 一 二 三 总分
得分
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的)
1.下面的图形是相似图形的是( )
2.在比例尺为1:80 000的北京市城区地图上,长安大街的长度约为4.75 cm,它的实际长度约为( )
A.3. 8km B.380m C.3 800 cm D.38 000m
3.如图,要说明△ABC∽△ACF,需要添加知件( )
B.∠ACB=∠F
C. AC=FC D.∠A=∠F
4.若 则 等于( )
A. B.1 C.2 D.5
5.用一个能放大5倍的放大镜看△ABC,则( )
A.△ABC放大后,∠A的度数是原来的5倍 B.△ABC放大后,面积是原来的5倍
C.△ABC放大后,面积是原来的10倍 D.△ABC放大后,周长是原来的5倍
6.如图,铁道口的栏道木短臂长为1米,长臂长为16米,当短臂下降0.5米时,长臂的端点升高( )米
A.8.5
B.8.4
C.8
D.8.3
7.如图,E 是平行四边形ABCD 的边BC 的延长线上的一点,连接AE交CD 于F,则图中共有相似三角形( )
A.1对 B.2对
C.3对 D.4对
8.如图,在 ABCD中,E是AD 边上的中点,连接BE,并延长BE 交CD 延长于点 F,则△EDF与△BCF的周长之比是( )
A.1:2
B.1:3
C.1:4
D.1:5
9.如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A'B'C,并把△ABC的边长放大到原来的2倍.设点 B 的对应点 B'的横坐标是a,则点 B 的横坐标是( )
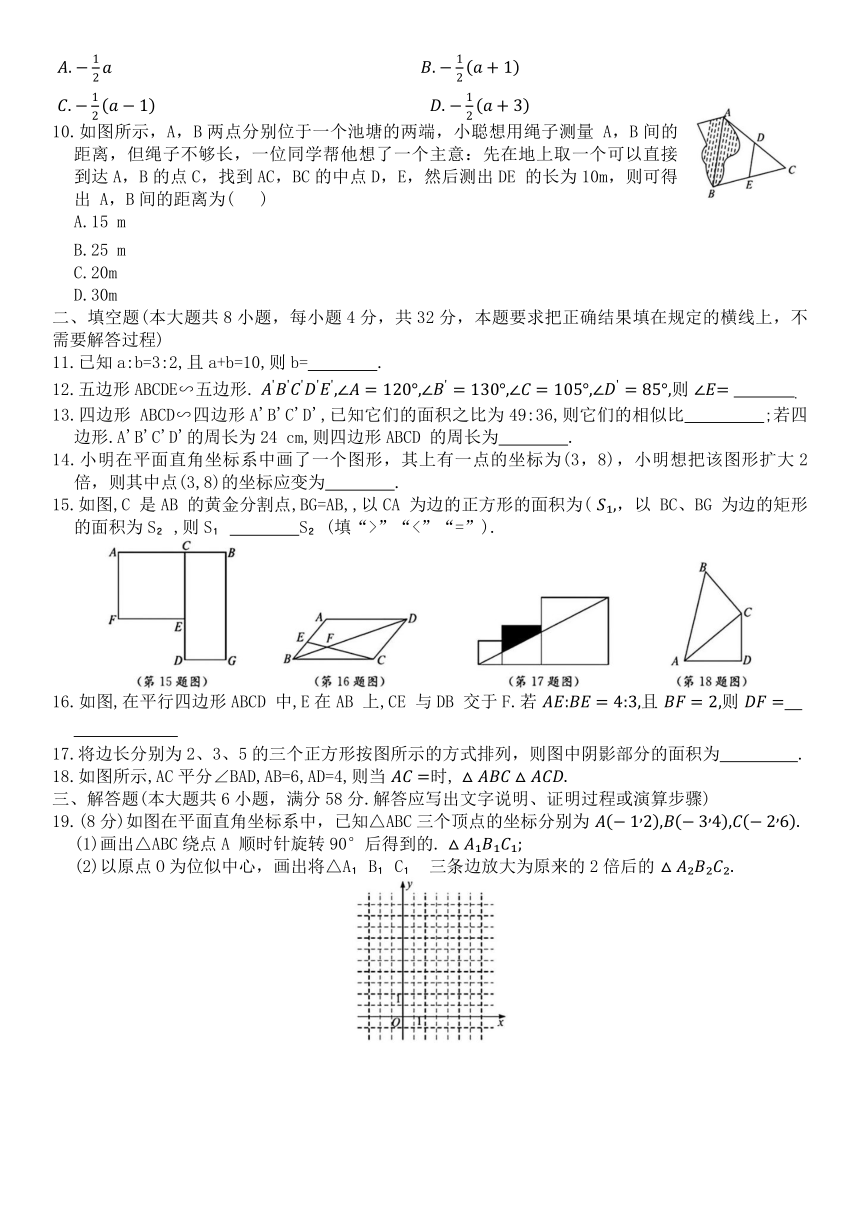
10.如图所示,A,B两点分别位于一个池塘的两端,小聪想用绳子测量 A,B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,找到AC,BC的中点D,E,然后测出DE 的长为10m,则可得出 A,B间的距离为( )
A.15 m
B.25 m
C.20m
D.30m
二、填空题(本大题共8小题,每小题4分,共32分,本题要求把正确结果填在规定的横线上,不需要解答过程)
11.已知a:b=3:2,且a+b=10,则b= .
12.五边形ABCDE∽五边形. 则
13.四边形 ABCD∽四边形A'B'C'D',已知它们的面积之比为49:36,则它们的相似比 ;若四边形.A'B'C'D'的周长为24 cm,则四边形ABCD 的周长为 .
14.小明在平面直角坐标系中画了一个图形,其上有一点的坐标为(3,8),小明想把该图形扩大2倍,则其中点(3,8)的坐标应变为 .
15.如图,C 是AB 的黄金分割点,BG=AB,,以CA 为边的正方形的面积为( ,以 BC、BG 为边的矩形的面积为S ,则S S (填“>”“<”“=”).
16.如图,在平行四边形ABCD 中,E在AB 上,CE 与DB 交于F.若 且 则
17.将边长分别为2、3、5的三个正方形按图所示的方式排列,则图中阴影部分的面积为 .
18.如图所示,AC平分∠BAD,AB=6,AD=4,则当 时,
三、解答题(本大题共6小题,满分58分.解答应写出文字说明、证明过程或演算步骤)
19.(8分)如图在平面直角坐标系中,已知△ABC三个顶点的坐标分别为
(1)画出△ABC绕点A 顺时针旋转90°后得到的.
(2)以原点O为位似中心,画出将△A B C 三条边放大为原来的2倍后的
20.(8分)如图已知 和 均为等边三角形,DF,EF分别交AC 于点H,G,且D,E分别在AB,BC上,请找出一个与 相似的三角形,并说明理由.
21.(10分)一般的室外放映的电影胶片上每一个图片的规格是 ,放映的荧屏的规格是2m×2m,若放映机的光源距胶片 20cm,问:荧屏放在离光源多远的地方时,放映的图象刚好布满整个荧屏
22.(10分)如图,等边三边形ABC 的边长为3,P 为BC 上一点,且 ,D 为AC 上一点,若 求CD的长.
23.(10分)如图所示,在矩形ABCD中,AC、BD 相交于点O,( 于E,连接DE交OC 于点F,作 于G.
(1)说明点 G 是线段BC 的一个三等分点;
(2)请你依照上面的画法,在原图上画出BC 的一个四等分点(保留作图痕迹,不必证明).
24.(12分)如图,在 中, ,AD 是BC边上的高,E是BC边上的一个动点(不与B,C重合), 垂足分别为 F,G.
(1)求证:
(2)FD 与DG 是否垂直 为什么
(3)当 时, 为等腰直角三角形吗 并说明理由.
第4章测试卷
1. B 2. A 3. B 4. D 5. D 6. C 7. C 8. A 9. D 10. C11.4 12.100° 13.7:6 28cm 14.(6,16)或(-6,-16)15.= 16. 17. 18.2
19.解(1)如图中,
(2)如图中△A B C (答案不唯一).
20.解 理由如下:
由题意,得
所以
因为 所以 120°,
所以
又 所以
21.解 如图,四边形 ABCD(胶片)与四边形 (荧屏)是位似图形,且位似比为 设四边形 距光源O的距离为xcm,
则有 得
又
即荧屏距光源 时,图象刚好布满整个荧屏.
22.解 由题意知∠B=∠C=60°,∠APD=60°,所以∠B=∠APD=60°.
又∠APC=∠APD+∠DPC=∠B+∠PAB,所以∠DPC=∠PAB.
在△DPC 和△PAB 中,因为∠B =∠C,∠DPC=∠PAB,
所以△DPC∽△PAB,所以
又AB=BC=AC=3,BP=1,
所以PC=BC-BP=3-1=2,
所以 所以
23.解 (1)∵OE⊥BC,FG⊥BC,∴OE∥CD.
∵△OEF∽△CDF,
∵四边形ABCD是矩形,∴AD∥BC.
∴G是BC的三等分点;
(2)依题意画图如下.
24.(1)证明 在△ADC和△EGC中,
(2)解 FD与DG 垂直.理由如下:
在四边形AFEG中,∵∠FAG=∠AFE=∠AGE=90°
∴四边形AFEG为矩形,∴AF=EG.
由(1)知
∵△ABC为直角三角形,AD⊥BC.
∴∠FAD=∠C,∴△AFD∽△CGD,
∴∠ADF=∠CDG.
又∠CDG+∠ADG=90°,∴∠ADF+∠ADG=90°,即∠FDG=90°,∴FD⊥DG.
(3)解当AB=AC时,△FDG为等腰直角三角形.理由如下:∵AB=AC,∠BAC=90°,∴AD=DC.
∴△FDG为等腰直角三角形.
(满分120分,时间120分钟)
题号 一 二 三 总分
得分
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的)
1.下面的图形是相似图形的是( )
2.在比例尺为1:80 000的北京市城区地图上,长安大街的长度约为4.75 cm,它的实际长度约为( )
A.3. 8km B.380m C.3 800 cm D.38 000m
3.如图,要说明△ABC∽△ACF,需要添加知件( )
B.∠ACB=∠F
C. AC=FC D.∠A=∠F
4.若 则 等于( )
A. B.1 C.2 D.5
5.用一个能放大5倍的放大镜看△ABC,则( )
A.△ABC放大后,∠A的度数是原来的5倍 B.△ABC放大后,面积是原来的5倍
C.△ABC放大后,面积是原来的10倍 D.△ABC放大后,周长是原来的5倍
6.如图,铁道口的栏道木短臂长为1米,长臂长为16米,当短臂下降0.5米时,长臂的端点升高( )米
A.8.5
B.8.4
C.8
D.8.3
7.如图,E 是平行四边形ABCD 的边BC 的延长线上的一点,连接AE交CD 于F,则图中共有相似三角形( )
A.1对 B.2对
C.3对 D.4对
8.如图,在 ABCD中,E是AD 边上的中点,连接BE,并延长BE 交CD 延长于点 F,则△EDF与△BCF的周长之比是( )
A.1:2
B.1:3
C.1:4
D.1:5
9.如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A'B'C,并把△ABC的边长放大到原来的2倍.设点 B 的对应点 B'的横坐标是a,则点 B 的横坐标是( )
10.如图所示,A,B两点分别位于一个池塘的两端,小聪想用绳子测量 A,B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,找到AC,BC的中点D,E,然后测出DE 的长为10m,则可得出 A,B间的距离为( )
A.15 m
B.25 m
C.20m
D.30m
二、填空题(本大题共8小题,每小题4分,共32分,本题要求把正确结果填在规定的横线上,不需要解答过程)
11.已知a:b=3:2,且a+b=10,则b= .
12.五边形ABCDE∽五边形. 则
13.四边形 ABCD∽四边形A'B'C'D',已知它们的面积之比为49:36,则它们的相似比 ;若四边形.A'B'C'D'的周长为24 cm,则四边形ABCD 的周长为 .
14.小明在平面直角坐标系中画了一个图形,其上有一点的坐标为(3,8),小明想把该图形扩大2倍,则其中点(3,8)的坐标应变为 .
15.如图,C 是AB 的黄金分割点,BG=AB,,以CA 为边的正方形的面积为( ,以 BC、BG 为边的矩形的面积为S ,则S S (填“>”“<”“=”).
16.如图,在平行四边形ABCD 中,E在AB 上,CE 与DB 交于F.若 且 则
17.将边长分别为2、3、5的三个正方形按图所示的方式排列,则图中阴影部分的面积为 .
18.如图所示,AC平分∠BAD,AB=6,AD=4,则当 时,
三、解答题(本大题共6小题,满分58分.解答应写出文字说明、证明过程或演算步骤)
19.(8分)如图在平面直角坐标系中,已知△ABC三个顶点的坐标分别为
(1)画出△ABC绕点A 顺时针旋转90°后得到的.
(2)以原点O为位似中心,画出将△A B C 三条边放大为原来的2倍后的
20.(8分)如图已知 和 均为等边三角形,DF,EF分别交AC 于点H,G,且D,E分别在AB,BC上,请找出一个与 相似的三角形,并说明理由.
21.(10分)一般的室外放映的电影胶片上每一个图片的规格是 ,放映的荧屏的规格是2m×2m,若放映机的光源距胶片 20cm,问:荧屏放在离光源多远的地方时,放映的图象刚好布满整个荧屏
22.(10分)如图,等边三边形ABC 的边长为3,P 为BC 上一点,且 ,D 为AC 上一点,若 求CD的长.
23.(10分)如图所示,在矩形ABCD中,AC、BD 相交于点O,( 于E,连接DE交OC 于点F,作 于G.
(1)说明点 G 是线段BC 的一个三等分点;
(2)请你依照上面的画法,在原图上画出BC 的一个四等分点(保留作图痕迹,不必证明).
24.(12分)如图,在 中, ,AD 是BC边上的高,E是BC边上的一个动点(不与B,C重合), 垂足分别为 F,G.
(1)求证:
(2)FD 与DG 是否垂直 为什么
(3)当 时, 为等腰直角三角形吗 并说明理由.
第4章测试卷
1. B 2. A 3. B 4. D 5. D 6. C 7. C 8. A 9. D 10. C11.4 12.100° 13.7:6 28cm 14.(6,16)或(-6,-16)15.= 16. 17. 18.2
19.解(1)如图中,
(2)如图中△A B C (答案不唯一).
20.解 理由如下:
由题意,得
所以
因为 所以 120°,
所以
又 所以
21.解 如图,四边形 ABCD(胶片)与四边形 (荧屏)是位似图形,且位似比为 设四边形 距光源O的距离为xcm,
则有 得
又
即荧屏距光源 时,图象刚好布满整个荧屏.
22.解 由题意知∠B=∠C=60°,∠APD=60°,所以∠B=∠APD=60°.
又∠APC=∠APD+∠DPC=∠B+∠PAB,所以∠DPC=∠PAB.
在△DPC 和△PAB 中,因为∠B =∠C,∠DPC=∠PAB,
所以△DPC∽△PAB,所以
又AB=BC=AC=3,BP=1,
所以PC=BC-BP=3-1=2,
所以 所以
23.解 (1)∵OE⊥BC,FG⊥BC,∴OE∥CD.
∵△OEF∽△CDF,
∵四边形ABCD是矩形,∴AD∥BC.
∴G是BC的三等分点;
(2)依题意画图如下.
24.(1)证明 在△ADC和△EGC中,
(2)解 FD与DG 垂直.理由如下:
在四边形AFEG中,∵∠FAG=∠AFE=∠AGE=90°
∴四边形AFEG为矩形,∴AF=EG.
由(1)知
∵△ABC为直角三角形,AD⊥BC.
∴∠FAD=∠C,∴△AFD∽△CGD,
∴∠ADF=∠CDG.
又∠CDG+∠ADG=90°,∴∠ADF+∠ADG=90°,即∠FDG=90°,∴FD⊥DG.
(3)解当AB=AC时,△FDG为等腰直角三角形.理由如下:∵AB=AC,∠BAC=90°,∴AD=DC.
∴△FDG为等腰直角三角形.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
