北师大版数学九年级上册第6章反比例函数测试卷(含答案)
文档属性
| 名称 | 北师大版数学九年级上册第6章反比例函数测试卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 688.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-31 00:00:00 | ||
图片预览



文档简介
第6章测试卷
(满分120分,时间120分钟)
题号 一 二 三 总分
得分
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的)
1.观察下列函数: 其中反比例函数有( )
A.1个 B.2个 C.3个 D.4个
2.已知y与x成正比例,z与y成反比例,那么z与x之间的关系是( )
A.成正比例 B.成反比例
C.有可能成正比例,也可能成反比例 D.无法确定
3.已知反比例函数的图象过点 M(-1,2),则此反比例函数的表达式为( )
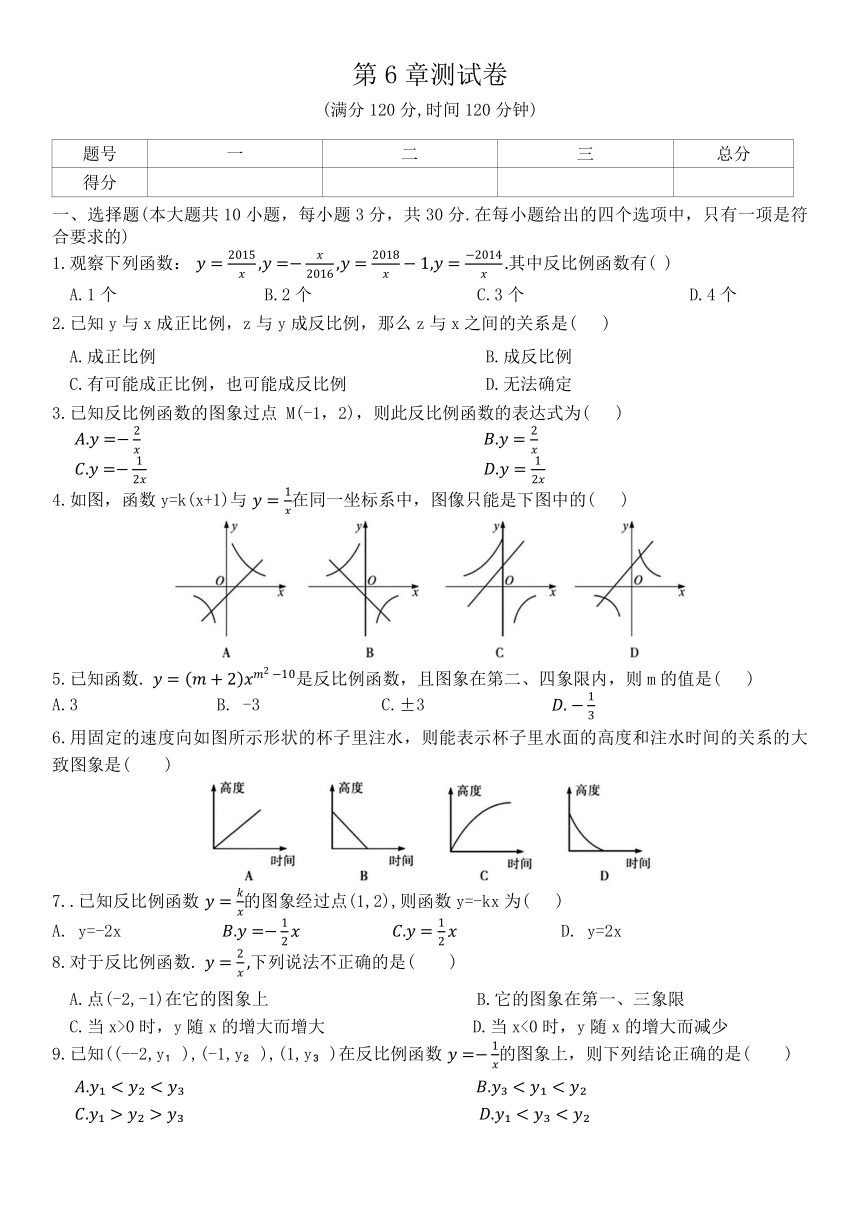
4.如图,函数y=k(x+1)与 在同一坐标系中,图像只能是下图中的( )
5.已知函数. 是反比例函数,且图象在第二、四象限内,则m的值是( )
A.3 B. -3 C.±3
6.用固定的速度向如图所示形状的杯子里注水,则能表示杯子里水面的高度和注水时间的关系的大致图象是( )
7..已知反比例函数 的图象经过点(1,2),则函数y=-kx为( )
A. y=-2x D. y=2x
8.对于反比例函数. 下列说法不正确的是( )
A.点(-2,-1)在它的图象上 B.它的图象在第一、三象限
C.当x>0时,y随x的增大而增大 D.当x<0时,y随x的增大而减少
9.已知((--2,y ),(-1,y ),(1,y )在反比例函数 的图象上,则下列结论正确的是( )
10.如图,直线 ,与函数 的图象分别交于点 A 、A 、A 、A 、…;与函数 的图象分别交于点. B 、B 、B 、….如果四边形A A B B 的面积记为S ,四边形. 的面积记为 S ,四边形 A A B B 的面积记为S ,…,以此类推.则 S 的值是( )
二、填空题(本大题共8小题,每小题4分,共32分,本题要求把正确结果填在规定的横线上,不需要解答过程)
11.某奶粉生产厂要制造一种容积为2升(1升=1立方分米)的圆柱形桶,桶的底面积s与桶高h有怎样的函数关系式 .
12.一水桶的下底面积是盖面积的2 倍,如果将其底朝下放在桌上,它对桌面的压强是600Pa,翻过来放,对桌面的压强是 .
13.已知函数 当x<0时,y 0,此时,其图象的相应部分在第 象限.
14.设函数 与y=x-1的图象的交点坐标为(a,b),则 的值为 .
15.老师在同一直角坐标系中画出了一个反比例函数的图象以及正比例函数. 的图象,请同学们观察有什么特点并说出来.同学甲:与直线y=-x有两个交点;同学乙:图象上任意一点到两坐标轴距离的积是5,请你根据同学甲和同学乙的说法,写出反比例函数的表达式: .
16.若反比例函数的图象经过点(2,-2),(m,1),m= .
17.如图,点 A在双曲线 上,,点B在双曲线. 上,且AB∥x轴,点C和点D在x轴上,若四边形AB-CD 为矩形,则矩形ABCD 的面积为 .
18.如图,直线 与双曲线 交于A,B两点,其横坐标分别为1 和5,则不等式 的解集是 .
三、解答题(本大题共6小题,满分58分.解答应写出文字说明、证明过程或演算步骤)
19.(8分)在下面的坐标系中,已经画出了一次函数y=x的图象.
(1)请你再画出反比例函数 的图象;
(2)根据图象直接写出x取什么范围的值时,一次函数的值比反比例函数的值小.
20.(8分)已知. 与x成反比例,y 与. 成正比例,并且当. 时, ;当x=1时,
(1)y与x的函数表达式;
(2)当 时,求y的值.
21.(10分)某服装厂承揽一项生产夏凉小衫1600件的任务,计划用t天完成.
(1)写出每天生产夏凉小衫w(件)与生产时间t(天)( 之间的函数关系式;
(2)由于气温提前升高,商家与服装厂商议调整计划,决定提前4天交货,那么服装厂每天要多做多少件夏凉小衫才能完成任务
22.(10分)如图,直线 与双曲线 在同一坐标系中的图像可能是相交于A(1,2),B(m,-1)两点.
(1)求直线和双曲线的表达式;
(2)若 为双曲线上的三点,且. 请直接写出 y ,y ,y 的大小关系;
(3)观察图象,请直接写出使不等式 成立的x的取值范围.
23.(10分)已知,如图,在平面直角坐标系xOy中,直线AB与x轴交于点. 0),与反比例函数在第一象限内的图象交于点 B(2,n),连接BO,若(
(1)求该反比例函 的表达式和直线 AB 的表达式;
(2)若直线AB与y 轴的交点为C,求 的面积.
24.(12 分)据媒体报道,近期“手足口病”可能进入发病高峰期,某校根据《学校卫生工作条例》,为预防“手足口病”,对教室进行“薰药消毒”.已知药物在燃烧及释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所示(即图中线段OA 和双曲线在A 点及其右侧的部分).根据图象所示信息,解答下列问题:
(1)写出药物燃烧及释放过程中,y与x之间的函数解析式及自变量的取值范围.
(2)据测定,当空气中每立方米的含药量低于2毫克时,对人体无毒害作用,那么从消毒开始后,哪一时间段内师生不能进入教室
第 6 章测试卷
1. B 2. B 3. A 4. D 5. B 6. C 7. A 8. C 9. B 10. D
12.1 200 Pa 13.> 二 14.—
16.-4 17.2 18.05
19.解(1)列表得:
x -4 --2 -1 1 2 4
y -1 -2 -4 4 2 1
描点,画图:
(2)当020.解(1)设 则
由题意,得 解得 所以y与x的函数表达式为
(2)当x=-1时, -15.
21.解(1)由题意可得,函数关系式为
答:每天多做 件夏凉小衫才能完成任务.
22.解(1)∵双曲线 经过点A(1,2),
双曲线的表达式为
∵点B(m,-1)在双曲线 上,
∴m=-2,则B(-2,-1).
由点A(1,2),B(-2,-1)在直线 上,得
解得
∴直线的表达式为y=x+1.
(3)x>1.或--223.解(1)由A(-2,0),得OA=2.
∵点 B(2,n)在第一象限内,S△AOB=4,
∴点B的坐标是(2,4).
设该反比例函数的表达式为
将点B的坐标代入 得(a=8.
∴反比例函数的表达式为
设直线AB的表达式为y=kx+b(k≠0),将点A,B的坐标分别代入,
得 解得
∴直线AB的表达式为y=x+2.
(2)在y=x+2中,令x=0,得y=2.∴点C的坐标是(0,2),∴OC=2.
24.解(1)设反比例函数的解析式为 将(25,6)代入解析式,得k=25×6=150,则反比例函数的解析式为y= 将y=10代入 得x=15,故A(15,10).所以反比例函数自变量的取值范围为x≥15.
设正比例函数的解析式为y=nx,将A(15,10)代入,得 则正比例函数的解析式为 15).
(2)由 解得x=3;由 解得x=75.所以从消毒开始后,从第3分钟开始直至第75分钟内,师生不能进入教室.
(满分120分,时间120分钟)
题号 一 二 三 总分
得分
一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的)
1.观察下列函数: 其中反比例函数有( )
A.1个 B.2个 C.3个 D.4个
2.已知y与x成正比例,z与y成反比例,那么z与x之间的关系是( )
A.成正比例 B.成反比例
C.有可能成正比例,也可能成反比例 D.无法确定
3.已知反比例函数的图象过点 M(-1,2),则此反比例函数的表达式为( )
4.如图,函数y=k(x+1)与 在同一坐标系中,图像只能是下图中的( )
5.已知函数. 是反比例函数,且图象在第二、四象限内,则m的值是( )
A.3 B. -3 C.±3
6.用固定的速度向如图所示形状的杯子里注水,则能表示杯子里水面的高度和注水时间的关系的大致图象是( )
7..已知反比例函数 的图象经过点(1,2),则函数y=-kx为( )
A. y=-2x D. y=2x
8.对于反比例函数. 下列说法不正确的是( )
A.点(-2,-1)在它的图象上 B.它的图象在第一、三象限
C.当x>0时,y随x的增大而增大 D.当x<0时,y随x的增大而减少
9.已知((--2,y ),(-1,y ),(1,y )在反比例函数 的图象上,则下列结论正确的是( )
10.如图,直线 ,与函数 的图象分别交于点 A 、A 、A 、A 、…;与函数 的图象分别交于点. B 、B 、B 、….如果四边形A A B B 的面积记为S ,四边形. 的面积记为 S ,四边形 A A B B 的面积记为S ,…,以此类推.则 S 的值是( )
二、填空题(本大题共8小题,每小题4分,共32分,本题要求把正确结果填在规定的横线上,不需要解答过程)
11.某奶粉生产厂要制造一种容积为2升(1升=1立方分米)的圆柱形桶,桶的底面积s与桶高h有怎样的函数关系式 .
12.一水桶的下底面积是盖面积的2 倍,如果将其底朝下放在桌上,它对桌面的压强是600Pa,翻过来放,对桌面的压强是 .
13.已知函数 当x<0时,y 0,此时,其图象的相应部分在第 象限.
14.设函数 与y=x-1的图象的交点坐标为(a,b),则 的值为 .
15.老师在同一直角坐标系中画出了一个反比例函数的图象以及正比例函数. 的图象,请同学们观察有什么特点并说出来.同学甲:与直线y=-x有两个交点;同学乙:图象上任意一点到两坐标轴距离的积是5,请你根据同学甲和同学乙的说法,写出反比例函数的表达式: .
16.若反比例函数的图象经过点(2,-2),(m,1),m= .
17.如图,点 A在双曲线 上,,点B在双曲线. 上,且AB∥x轴,点C和点D在x轴上,若四边形AB-CD 为矩形,则矩形ABCD 的面积为 .
18.如图,直线 与双曲线 交于A,B两点,其横坐标分别为1 和5,则不等式 的解集是 .
三、解答题(本大题共6小题,满分58分.解答应写出文字说明、证明过程或演算步骤)
19.(8分)在下面的坐标系中,已经画出了一次函数y=x的图象.
(1)请你再画出反比例函数 的图象;
(2)根据图象直接写出x取什么范围的值时,一次函数的值比反比例函数的值小.
20.(8分)已知. 与x成反比例,y 与. 成正比例,并且当. 时, ;当x=1时,
(1)y与x的函数表达式;
(2)当 时,求y的值.
21.(10分)某服装厂承揽一项生产夏凉小衫1600件的任务,计划用t天完成.
(1)写出每天生产夏凉小衫w(件)与生产时间t(天)( 之间的函数关系式;
(2)由于气温提前升高,商家与服装厂商议调整计划,决定提前4天交货,那么服装厂每天要多做多少件夏凉小衫才能完成任务
22.(10分)如图,直线 与双曲线 在同一坐标系中的图像可能是相交于A(1,2),B(m,-1)两点.
(1)求直线和双曲线的表达式;
(2)若 为双曲线上的三点,且. 请直接写出 y ,y ,y 的大小关系;
(3)观察图象,请直接写出使不等式 成立的x的取值范围.
23.(10分)已知,如图,在平面直角坐标系xOy中,直线AB与x轴交于点. 0),与反比例函数在第一象限内的图象交于点 B(2,n),连接BO,若(
(1)求该反比例函 的表达式和直线 AB 的表达式;
(2)若直线AB与y 轴的交点为C,求 的面积.
24.(12 分)据媒体报道,近期“手足口病”可能进入发病高峰期,某校根据《学校卫生工作条例》,为预防“手足口病”,对教室进行“薰药消毒”.已知药物在燃烧及释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所示(即图中线段OA 和双曲线在A 点及其右侧的部分).根据图象所示信息,解答下列问题:
(1)写出药物燃烧及释放过程中,y与x之间的函数解析式及自变量的取值范围.
(2)据测定,当空气中每立方米的含药量低于2毫克时,对人体无毒害作用,那么从消毒开始后,哪一时间段内师生不能进入教室
第 6 章测试卷
1. B 2. B 3. A 4. D 5. B 6. C 7. A 8. C 9. B 10. D
12.1 200 Pa 13.> 二 14.—
16.-4 17.2 18.0
19.解(1)列表得:
x -4 --2 -1 1 2 4
y -1 -2 -4 4 2 1
描点,画图:
(2)当0
由题意,得 解得 所以y与x的函数表达式为
(2)当x=-1时, -15.
21.解(1)由题意可得,函数关系式为
答:每天多做 件夏凉小衫才能完成任务.
22.解(1)∵双曲线 经过点A(1,2),
双曲线的表达式为
∵点B(m,-1)在双曲线 上,
∴m=-2,则B(-2,-1).
由点A(1,2),B(-2,-1)在直线 上,得
解得
∴直线的表达式为y=x+1.
(3)x>1.或--2
∵点 B(2,n)在第一象限内,S△AOB=4,
∴点B的坐标是(2,4).
设该反比例函数的表达式为
将点B的坐标代入 得(a=8.
∴反比例函数的表达式为
设直线AB的表达式为y=kx+b(k≠0),将点A,B的坐标分别代入,
得 解得
∴直线AB的表达式为y=x+2.
(2)在y=x+2中,令x=0,得y=2.∴点C的坐标是(0,2),∴OC=2.
24.解(1)设反比例函数的解析式为 将(25,6)代入解析式,得k=25×6=150,则反比例函数的解析式为y= 将y=10代入 得x=15,故A(15,10).所以反比例函数自变量的取值范围为x≥15.
设正比例函数的解析式为y=nx,将A(15,10)代入,得 则正比例函数的解析式为 15).
(2)由 解得x=3;由 解得x=75.所以从消毒开始后,从第3分钟开始直至第75分钟内,师生不能进入教室.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
