22.3实际问题与二次函数 同步练习(含答案)2024-2025学年人教版数学九年级上册
文档属性
| 名称 | 22.3实际问题与二次函数 同步练习(含答案)2024-2025学年人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 821.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-31 00:00:00 | ||
图片预览

文档简介
22.3 实际问题与二次函数
一、单选题
1.如图,某农场计划修建三间矩形饲养室,饲养室一面靠现有墙(墙可用长),中间用两道墙隔开,已知计划中的修筑材料可建围墙总长为,设饲养室宽为,占地总面积为,则三间饲养室总面积有( )
A.最小值 B.最小值 C.最大值 D.最大值
2.如图,以的速度将小球沿与地面成角的方向击出时,小球的飞行路线将是一条拋物线.如果不考虑空气阻力,小球的飞行高度(单位:m)与飞行时间(单位:)之间具有函数关系.有下列结论:①小球从飞出到落地用时为;②小球飞行的最大高度为;③小球的飞行高度为时,小球飞行的时间是.其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
3.某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.有下列结论:①降价8元时,数量为36件.②若商场平均每天要盈利1200元,每件衬衫应降价10元.③商场平均每天盈利最多为1250元.正确结论的个数是( )
A.0 B.1 C.2 D.3
4.如图所示,某工厂的大门是抛物线形水泥建筑物,大门的地面宽度为,两侧距地面高处各有一壁灯,两壁灯间的水平距离为,则厂门的高度约为( )
A. B. C. D.
5.北京时间2023年5月30日,搭载神舟十六号载人飞船的长征二号F遥十六运载火箭在酒泉卫星发射中心点火发射,发射取得圆满成功.某校九年级学生做炮弹模拟发射实验,其运动轨迹可以近似看成抛物线,若此炮弹在第6秒和第12秒时的高度一致,则该炮弹到地面上时,所经过的时间为( )
A.第6秒 B.第9秒 C.第12秒 D.第18秒
6.抛物线与直线交于,两点,抛物线在,两点之间的部分以及线段所围域内(包括边界)恰有4个整点(横、纵坐标都是整数的点叫做整点),则的取值范围是( )
A. B. C. D.
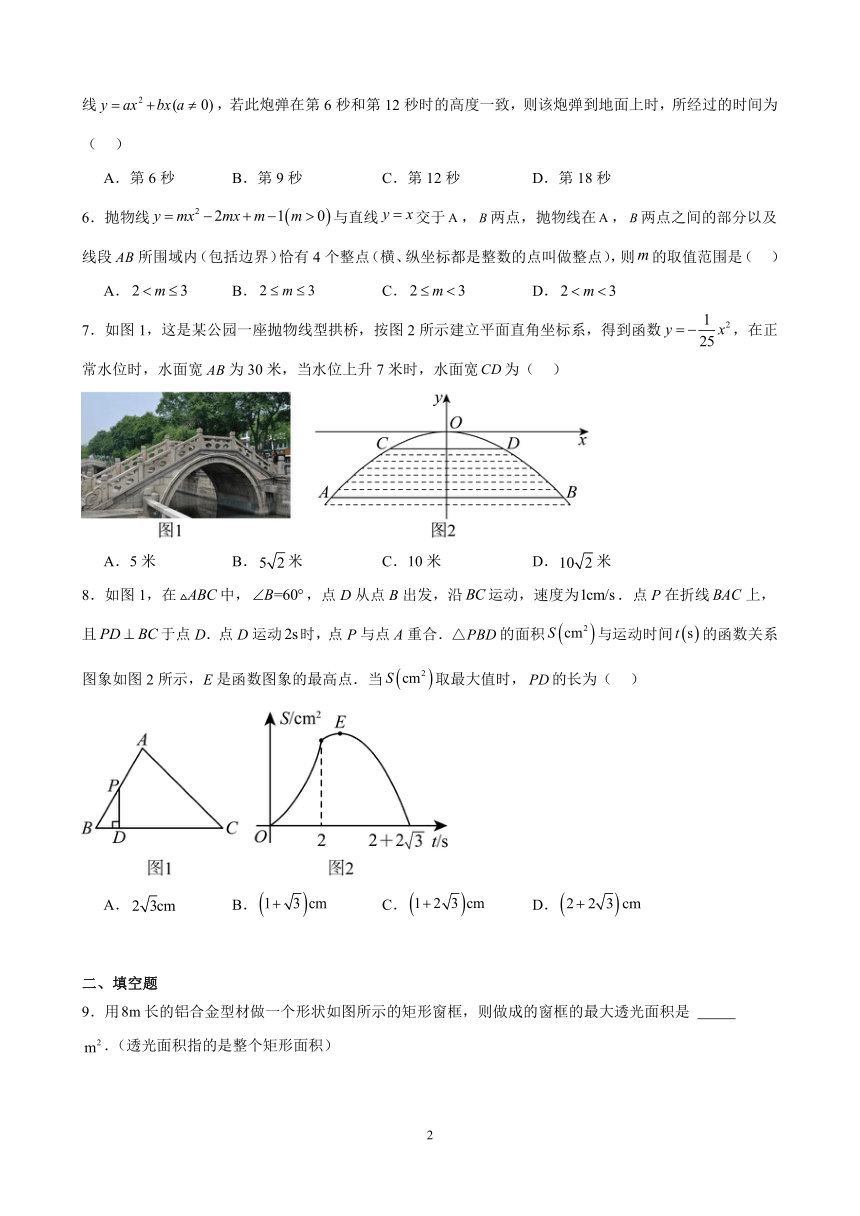
7.如图1,这是某公园一座抛物线型拱桥,按图2所示建立平面直角坐标系,得到函数,在正常水位时,水面宽为30米,当水位上升7米时,水面宽为( )
A.5米 B.米 C.10米 D.米
8.如图1,在中,,点D从点B出发,沿运动,速度为.点P在折线上,且于点D.点D运动时,点P与点A重合.的面积与运动时间的函数关系图象如图2所示,E是函数图象的最高点.当取最大值时,的长为( )
A. B. C. D.
二、填空题
9.用长的铝合金型材做一个形状如图所示的矩形窗框,则做成的窗框的最大透光面积是 .(透光面积指的是整个矩形面积)
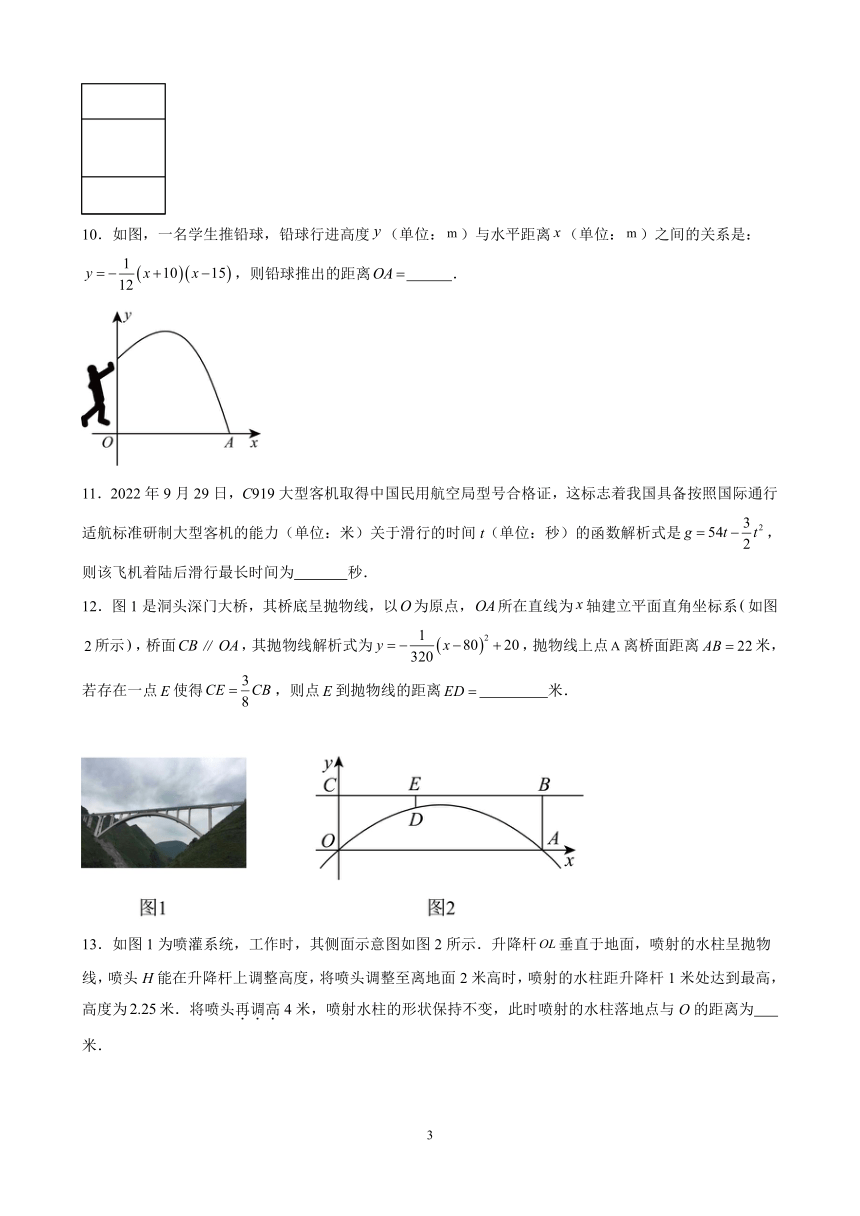
10.如图,一名学生推铅球,铅球行进高度(单位:)与水平距离(单位:)之间的关系是:,则铅球推出的距离 .
11.2022年9月29日,C919大型客机取得中国民用航空局型号合格证,这标志着我国具备按照国际通行适航标准研制大型客机的能力(单位:米)关于滑行的时间t(单位:秒)的函数解析式是,则该飞机着陆后滑行最长时间为 秒.
12.图1是洞头深门大桥,其桥底呈抛物线,以为原点,所在直线为轴建立平面直角坐标系如图所示,桥面,其抛物线解析式为,抛物线上点离桥面距离米,若存在一点使得,则点到抛物线的距离 米.
13.如图1为喷灌系统,工作时,其侧面示意图如图2所示.升降杆垂直于地面,喷射的水柱呈抛物线,喷头H能在升降杆上调整高度,将喷头调整至离地面2米高时,喷射的水柱距升降杆1米处达到最高,高度为米.将喷头再调高4米,喷射水柱的形状保持不变,此时喷射的水柱落地点与O的距离为 米.
14.如图,在平面直角坐标系中,A、B、C三点的坐标分别为,,,点为线段上的一个动点,连接,过点P作交y轴于点Q,当点在上运动时,点Q随之运动,设点Q的坐标为,则的取值范围是 .
三、解答题
15.如图,有长为24米的篱笆,一面利用墙(墙的最大可用长度为9米)围成中间隔有一道篱笆的长方形花圃.设花圃边为米,面积为平方米.
(1)写出与的函数关系式 ,并写出的取值范围 ;
(2)如果要围成面积为的花圃,求的长度;
(3)如果要使围成的花圃面积最大,求最大面积是多少平方米.
16.某商品的进价为每件40元,当售价为每件50元时,每月可卖出200件,如果售价每上涨1元,则每月少卖10件(每件售价不能高于65元);如果售价每下降1元,则每月多卖12件(每件售价不低于48元).设每件商品的售价为元(为正整数),每月的销售量为件.
(1)①当售价上涨时,与的函数关系为______,自变量的取值范围是______;
②当售价下降时,与的函数关系为______,自变量的取值范围是______;
(2)每件商品的售价定为多少元时,每月可获得利润最大?最大月利润是多少元?
17.如图,一小球从点A处以4米/秒的速度水平匀速抛出,下落过程中水平方向速度不变,忽略空气阻力,点M是下落路线的某位置,点A,点M的竖直距离h(米)与飞出时间t(秒)的平方成正比,且秒时,米.
(1)求h关于t的函数表达式.
(2)已知A点的离地高度为米,求小球的落地位置P点与A点的水平距离.
参考答案:
1.C
2.C
3.C
4.C
5.D
6.A
7.D
8.B
9.
10.
11.18
12.
13.
14.
15.(1),
(2)6米
(3)的长为5米,围成的花圃面积最大,最大面积是45平方米
16.(1)①;;②;
(2)当售价为元时,利润最大利润为元
17.(1)
(2)
一、单选题
1.如图,某农场计划修建三间矩形饲养室,饲养室一面靠现有墙(墙可用长),中间用两道墙隔开,已知计划中的修筑材料可建围墙总长为,设饲养室宽为,占地总面积为,则三间饲养室总面积有( )
A.最小值 B.最小值 C.最大值 D.最大值
2.如图,以的速度将小球沿与地面成角的方向击出时,小球的飞行路线将是一条拋物线.如果不考虑空气阻力,小球的飞行高度(单位:m)与飞行时间(单位:)之间具有函数关系.有下列结论:①小球从飞出到落地用时为;②小球飞行的最大高度为;③小球的飞行高度为时,小球飞行的时间是.其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
3.某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.有下列结论:①降价8元时,数量为36件.②若商场平均每天要盈利1200元,每件衬衫应降价10元.③商场平均每天盈利最多为1250元.正确结论的个数是( )
A.0 B.1 C.2 D.3
4.如图所示,某工厂的大门是抛物线形水泥建筑物,大门的地面宽度为,两侧距地面高处各有一壁灯,两壁灯间的水平距离为,则厂门的高度约为( )
A. B. C. D.
5.北京时间2023年5月30日,搭载神舟十六号载人飞船的长征二号F遥十六运载火箭在酒泉卫星发射中心点火发射,发射取得圆满成功.某校九年级学生做炮弹模拟发射实验,其运动轨迹可以近似看成抛物线,若此炮弹在第6秒和第12秒时的高度一致,则该炮弹到地面上时,所经过的时间为( )
A.第6秒 B.第9秒 C.第12秒 D.第18秒
6.抛物线与直线交于,两点,抛物线在,两点之间的部分以及线段所围域内(包括边界)恰有4个整点(横、纵坐标都是整数的点叫做整点),则的取值范围是( )
A. B. C. D.
7.如图1,这是某公园一座抛物线型拱桥,按图2所示建立平面直角坐标系,得到函数,在正常水位时,水面宽为30米,当水位上升7米时,水面宽为( )
A.5米 B.米 C.10米 D.米
8.如图1,在中,,点D从点B出发,沿运动,速度为.点P在折线上,且于点D.点D运动时,点P与点A重合.的面积与运动时间的函数关系图象如图2所示,E是函数图象的最高点.当取最大值时,的长为( )
A. B. C. D.
二、填空题
9.用长的铝合金型材做一个形状如图所示的矩形窗框,则做成的窗框的最大透光面积是 .(透光面积指的是整个矩形面积)
10.如图,一名学生推铅球,铅球行进高度(单位:)与水平距离(单位:)之间的关系是:,则铅球推出的距离 .
11.2022年9月29日,C919大型客机取得中国民用航空局型号合格证,这标志着我国具备按照国际通行适航标准研制大型客机的能力(单位:米)关于滑行的时间t(单位:秒)的函数解析式是,则该飞机着陆后滑行最长时间为 秒.
12.图1是洞头深门大桥,其桥底呈抛物线,以为原点,所在直线为轴建立平面直角坐标系如图所示,桥面,其抛物线解析式为,抛物线上点离桥面距离米,若存在一点使得,则点到抛物线的距离 米.
13.如图1为喷灌系统,工作时,其侧面示意图如图2所示.升降杆垂直于地面,喷射的水柱呈抛物线,喷头H能在升降杆上调整高度,将喷头调整至离地面2米高时,喷射的水柱距升降杆1米处达到最高,高度为米.将喷头再调高4米,喷射水柱的形状保持不变,此时喷射的水柱落地点与O的距离为 米.
14.如图,在平面直角坐标系中,A、B、C三点的坐标分别为,,,点为线段上的一个动点,连接,过点P作交y轴于点Q,当点在上运动时,点Q随之运动,设点Q的坐标为,则的取值范围是 .
三、解答题
15.如图,有长为24米的篱笆,一面利用墙(墙的最大可用长度为9米)围成中间隔有一道篱笆的长方形花圃.设花圃边为米,面积为平方米.
(1)写出与的函数关系式 ,并写出的取值范围 ;
(2)如果要围成面积为的花圃,求的长度;
(3)如果要使围成的花圃面积最大,求最大面积是多少平方米.
16.某商品的进价为每件40元,当售价为每件50元时,每月可卖出200件,如果售价每上涨1元,则每月少卖10件(每件售价不能高于65元);如果售价每下降1元,则每月多卖12件(每件售价不低于48元).设每件商品的售价为元(为正整数),每月的销售量为件.
(1)①当售价上涨时,与的函数关系为______,自变量的取值范围是______;
②当售价下降时,与的函数关系为______,自变量的取值范围是______;
(2)每件商品的售价定为多少元时,每月可获得利润最大?最大月利润是多少元?
17.如图,一小球从点A处以4米/秒的速度水平匀速抛出,下落过程中水平方向速度不变,忽略空气阻力,点M是下落路线的某位置,点A,点M的竖直距离h(米)与飞出时间t(秒)的平方成正比,且秒时,米.
(1)求h关于t的函数表达式.
(2)已知A点的离地高度为米,求小球的落地位置P点与A点的水平距离.
参考答案:
1.C
2.C
3.C
4.C
5.D
6.A
7.D
8.B
9.
10.
11.18
12.
13.
14.
15.(1),
(2)6米
(3)的长为5米,围成的花圃面积最大,最大面积是45平方米
16.(1)①;;②;
(2)当售价为元时,利润最大利润为元
17.(1)
(2)
同课章节目录
