广西壮族自治区南宁市第三中学2023-2024学年高一下学期期末考试数学试卷(含解析)
文档属性
| 名称 | 广西壮族自治区南宁市第三中学2023-2024学年高一下学期期末考试数学试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-31 00:00:00 | ||
图片预览




文档简介
南宁市第三中学2023-2024学年高一下学期期末考试数学试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.已知复数,则z的虚部是( )
A.4 B. C.3 D.3i
2.某工厂生产甲、乙、丙、丁四种不同型号的产品,产量分别为200,400,300,100件,为检验产品的质量,现用按比例分层随机抽样的方法从以上所有的产品中抽取60件进行检验,则应从乙种型号的产品中抽取件数为( )
A.24 B.9 C.36 D.18
3.四名同学各掷骰子5次,并各自记录每次骰子出现的点数,分别统计四名同学的记录结果,可以判断出一定没有出现点数6的是( )
A. 平均数为3,中位数2 B. 中位数为3,众数为2
C. 中位数为3,方差为2.8 D. 平均数为2,方差为2.4
4.已知在平行四边形中,E为上靠近点A的三等分点,设,,则( )
A. B. C. D.
5.已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的体积为( )
A. B. C. D.
6.已知向量,,若与方向相反,则实数的值为( )
A.4 B.2或 C. D.或4
7.在《九章算术》中,将四个面都是直角三角形的四面体称为鳖臑.在鳖臑中,平面,,,,则此四面体的外接球表面积为( )
A. B. C. D.
8.有6个相同的球,分别标有数字1,2,3,4,5,6,从中有放回地随机取两次,每次取1个球.甲表示事件“第一次取出的球的数字是4”,乙表示事件“第二次取出的球的数字是5”,丙表示事件“两次取出的球的数字之和是6”,丁表示事件“两次取出的球的数字之和是7”,则( )
A.甲与乙互斥 B.丙发生的概率为
C.甲与丁相互独立 D.乙与丙相互独立
二、多项选择题
9.在中,角A,B,C所对的边分别为a,b,c,下列说法中正确的是( )
A.若,则是等腰三角形
B.若,,,则
C.若,,,则
D.若面积为,则
10.某市2023年经过招商引资后,经济收入较前一年增加了一倍,实现翻番,为更好地了解该市的经济收入的变化情况,统计了该市招商引资前后的年经济收入构成比例,得到如下扇形图.则下列结论中正确的是( )
A.招商引资后,工资净收入较前一年减少
B.招商引资后,转移净收入是前一年的2.5倍
C.招商引资后,转移净收入与财产净收入的总和超过了该年经济收入的
D.招商引资后,经营净收入较前一年增加了一倍
11.如图,直四棱柱中,底面是,的矩形,直四棱柱的高为4,E,F分别为棱,的中点,则下列说法中正确的有( )
A.直线与相交
B.异面直线与所成角为
C.二面角的平面角为
D.平面截该长方体所得的截面为五边形
三、填空题
12.已知,,则________.
13.已知互不相等的4个正整数从小到大排序为x,y,z,6.若这4个数据的极差是中位数的2倍,则这4个数据的第75百分位数为________.
14.已知的内角A,B,C所对的边分别是a,b,c,点D是AB的中点.若且,,则________.
四、解答题
15.已知向量与的夹角,且,.
(1)求;
(2)求.
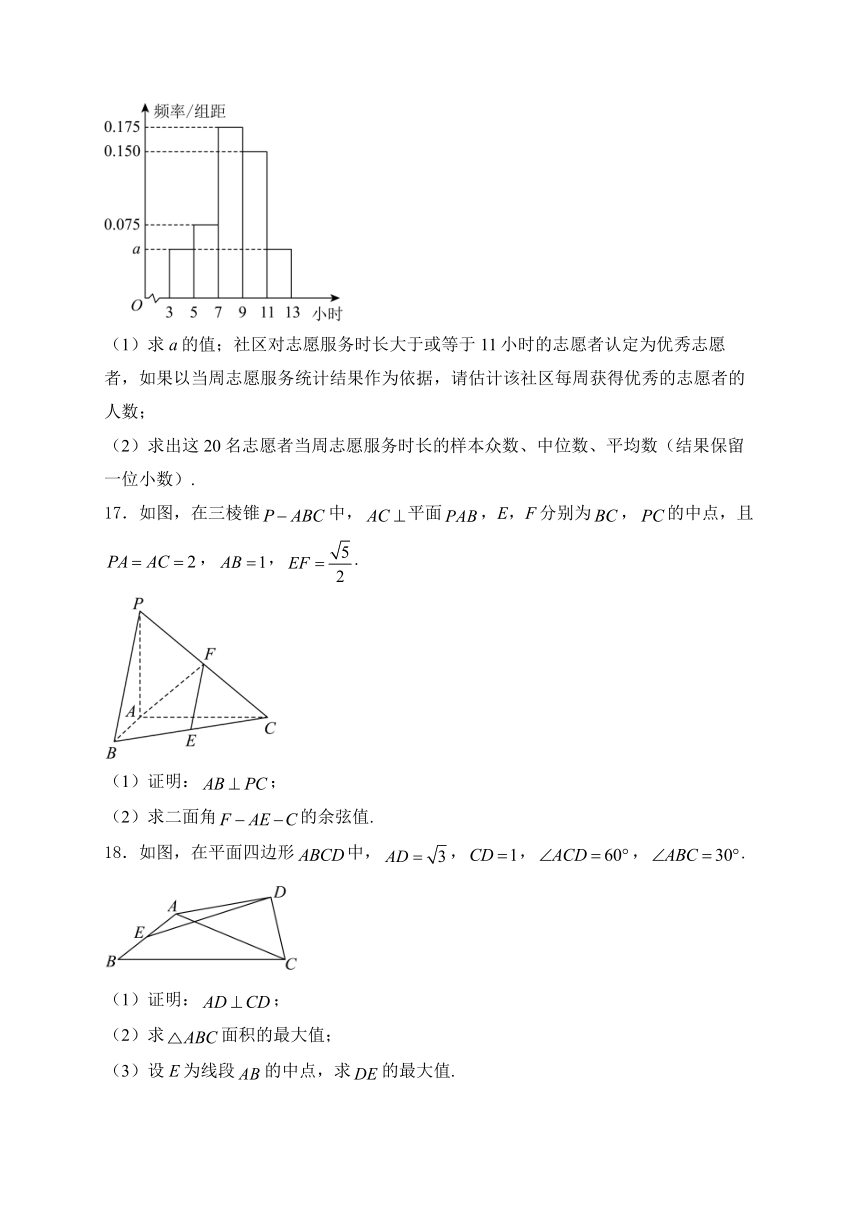
16.某社区为了解志愿者每周志愿服务的时长,在全社区300名志愿者中随机抽取20名志愿者在某个星期的志愿服务记录,统计他们当周在社区的志愿服务时长,按时长分组,得到频率分布直方图如图所示:
(1)求a的值;社区对志愿服务时长大于或等于11小时的志愿者认定为优秀志愿者,如果以当周志愿服务统计结果作为依据,请估计该社区每周获得优秀的志愿者的人数;
(2)求出这20名志愿者当周志愿服务时长的样本众数、中位数、平均数(结果保留一位小数).
17.如图,在三棱锥中,平面,E,F分别为,的中点,且,,.
(1)证明:;
(2)求二面角的余弦值.
18.如图,在平面四边形中,,,,.
(1)证明:;
(2)求面积的最大值;
(3)设E为线段的中点,求的最大值.
19.在某抽奖活动中,初始时的袋子中有3个除颜色外其余都相同的小球,颜色为2白1红.每次随机抽取一个小球后放回.抽奖规则如下:设定抽中红球为中奖,抽中白球为未中奖;若抽到白球,放回后把袋中的一个白色小球替换为红色;若抽到红球,放回后把三个球的颜色重新变为2白1红的初始状态.记第n次抽奖中奖的概率为.
(1)求,,;
(2)若存在实数a,b,c,对任意的不小于4的正整数n,都有,试确定a,b,c的值,并说明理由;
(3)若累计中奖4次及以上可以获得一枚优胜者勋章,则从初始状态下连抽9次获得至少一枚勋章的概率为多少?
参考答案
1.答案:C
解析:根据题意,,
所以z的虚部是3.
故选:C
2.答案:A
解析:产品总数为件,而抽取60件进行检验,
抽样比例为,则应从乙种型号的产品中抽取件,
故选:A
3.答案:D
解析:对于A,当投掷骰子出现结果为1,1,2,5,6时,满足平均数为3,中位数为2,可以出现点数6,故A错误;
对于B,当投掷骰子出现结果为2,2,3,4,6时,满足中位数为3,众数为2,可以出现点数6,故B错误;
对于C,当投掷骰子出现结果为1,2,3,3,6时,满足中位数为3,
平均数为:,
方差为,
可以出现点数6,故C错误;
对于D,若平均数为2,且出现6点,则方差,
则平均数为2,方差为2.4时,一定没有出现点数6,故D正确.
故选:D.
4.答案:A
解析:
.
故选:A
5.答案:B
解析:设圆锥母线长为l,高为h,底面半径为,
则由,得,所以,
所以.
故选:B.
6.答案:A
解析:,,即或,
当时,,,,与的方向相反,成立;
当时,,,,与的方向相同,不成立.
.
故选:A
7.答案:B
解析:根据题意,平面,平面,所以,
又,,平面,所以平面,
将鳖臑补全成长方体,如图,
则此四面体的外接球的半径为,
其外接球的表面积为.
故选:B.
8.答案:C
解析:由题意可知,两点数和为6的所有可能为,,,,,两点数和为7的所有可能为,,,,,,,,,,
对于A选项,甲与乙可以同时发生,故选项A错误;
对于B选项,由上可知错误,故选项B错误;
对于C选项,,故选项C正确;
对于D选项,,故选项D错误.
故选:C.
9.答案:ACD
解析:对于A,因为,由正弦定理可得
,因为三角形内角和定理,得,
由正弦定理得,因此是等腰三角形,A正确;
对于B.由正弦定理得,
则或,B错误;
对于C,由余弦定理得,,解得,C正确;
对于D,因为面积为,又
所以,所以,显然,
则,,,D正确;
故选:ACD.
10.答案:BD
解析:根据题意,可设招商引资前的经济收入为a,则招商引资后的经济收入为;
对于A,由招商引资前后的年经济收入构成比例可知招商引资前的工资收入为,招商引资后的工资收入为,
可知招商引资后,工资净收入较前一年增多,即A错误;
对于B,招商引资前的转移净收入为,招商引资后的工资收入为,
即招商引资后,转移净收入是前一年的2.5倍,可得B正确;
对于C,由招商引资后的年经济收入构成比例可知转移净收入与财产净收入的总和占比为,小于,即C错误;
对于D,招商引资后的经营净收入为,招商引资前的经营净收入为,可得招商引资后,经营净收入较前一年增加了一倍,即D正确.
故选:BD
11.答案:AD
解析:因为且,可得四边形为梯形,
所以与必相交,所以A正确;
由题意,在长方体中,因为平面,
平面,所以,
假设异面直线与所成角是,即,
平面,,
可得平面,而平面,
则,
在长方形中,因为,,
取中点F,可知正方形中,
可得与不垂直,矛盾,
所以异面直线与所成角不是,所以B错误;
由上图可知,又,即,则,
又平面,平面,所以,
,平面,所以平面,
平面,则,则为二面角的平面角,
又,所以不等于,C错误;
点P是棱上一点,且,取的中点M,连接,,,
因为F,P分别是和的中点,所以,
由四边形为平行四边形,所以,
因为平面平面,所以为平面与平面的交线,
,,为截面的边,截面又与平面及相交,
可得截面的两条边,所以截面共有五边形,所以D正确.
故选:AD.
12.答案:
解析:,
故答案为:.
13.答案:/
解析:易知这4个数据的极差为,中位数为,
即可得,所以;
又因为正整数x,y,z互不相等且,可得,,;
由为正数,因此这4个数据的第75百分位数为第三个数和第四个数的平均数,即,则这4个数据的第75百分位数为4.5.
故答案为:4.5
14.答案:
解析:根据题意,,由,即为,
由正弦定理得,
又因为,
所以,
因为,可得,所以
又因为为的一条中线,可得,
所以,
即,解得或(舍).
由余弦定理得.
故答案为:.
15.答案:(1)3;
(2)
解析:(1)因为向量与的夹角,且,,
所以,
;
(2)
.
16.答案:(1)0.050,3
(2)8.0,8.4,8.3
解析:(1)由题意,解得,
因为优秀志愿者的频率为,
所以估计该社区每周获得优秀的志愿者的人数有:人;
(2)由图可知这20名志愿者当周志愿服务时长的样本众数为,
设中位数为x,服务时长在小时的频率为,
服务时长在小时的频率为,
所以,而,解得,
这20名志愿者当周志愿服务时长的样本平均数为.
17.答案:(1)证明见解析;
(2)
解析:(1)E,F分别为,的中点,
,.平面,
.,平面,
平面,平面,.
(2)
根据题意,取的中点M,过M作交于N,连接,,,因为F为中点,M为的中点,则,且,
又,,,平面,
平面,
平面,而平面,,
又,,平面,
所以平面,
平面,,即为二面角的平面角,
所以在中,,,则,
由等面积可得,
所以,则,
即二面角的余弦值为.
18.答案:(1)证明见解析;
(2);
(3)3
解析:(1)由题知,在中,由正弦定理得,
因为,所以,所以,
所以,所以.
(2)在中,,
由余弦定理知:,
所以,所以,
解得,等号当仅当时取等号,
所以,.
(3)在中,设,则,则,
由正弦定理知:,
所以,,
在中,由余弦定理知,
所以
,
所以,等号当仅当时,即当时取等号,所以的最大值等于3.
19.答案:(1),,;
(2),,;
(3)
解析:(1),
,
;
(2)因为每次中奖后袋中的球会回到初始状态,
从初始状态开始,若第一次中奖,此时第n次抽奖中奖的概率为,
从初始状态开始,若第一次未中奖而第二次中奖,
此时第n次抽奖中奖的概率为,
从初始状态开始,若前两次均未中奖,则第三次必中奖,
此时第n次抽奖中奖的概率为,
综上所述,对任意的,,
又,所以,,;
(3)由题意知每抽三次至少有一次中奖,故连抽9次至少中奖3次,
所以只需排除3次中奖的情况即可获得一枚优胜者勋章,
另外,每两次中奖的间隔不能超过三次,每次中奖后袋中的球会回到初始状态,从初始状态开始,抽一次中奖的概率为,
从初始状态开始抽两次,第一次未中奖而第二次中奖的概率为,
从初始状态开始抽三次,前两次均未中奖而第三次中奖的概率为,
用表示第i次,第j次,第k次中奖,其余未中奖,
则三次中奖的所有情况如下:,,,,,,,,,,
故仅三次中奖的概率为
,
所以从初始状态下连抽9次获得至少一枚勋章的概率为.
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.已知复数,则z的虚部是( )
A.4 B. C.3 D.3i
2.某工厂生产甲、乙、丙、丁四种不同型号的产品,产量分别为200,400,300,100件,为检验产品的质量,现用按比例分层随机抽样的方法从以上所有的产品中抽取60件进行检验,则应从乙种型号的产品中抽取件数为( )
A.24 B.9 C.36 D.18
3.四名同学各掷骰子5次,并各自记录每次骰子出现的点数,分别统计四名同学的记录结果,可以判断出一定没有出现点数6的是( )
A. 平均数为3,中位数2 B. 中位数为3,众数为2
C. 中位数为3,方差为2.8 D. 平均数为2,方差为2.4
4.已知在平行四边形中,E为上靠近点A的三等分点,设,,则( )
A. B. C. D.
5.已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的体积为( )
A. B. C. D.
6.已知向量,,若与方向相反,则实数的值为( )
A.4 B.2或 C. D.或4
7.在《九章算术》中,将四个面都是直角三角形的四面体称为鳖臑.在鳖臑中,平面,,,,则此四面体的外接球表面积为( )
A. B. C. D.
8.有6个相同的球,分别标有数字1,2,3,4,5,6,从中有放回地随机取两次,每次取1个球.甲表示事件“第一次取出的球的数字是4”,乙表示事件“第二次取出的球的数字是5”,丙表示事件“两次取出的球的数字之和是6”,丁表示事件“两次取出的球的数字之和是7”,则( )
A.甲与乙互斥 B.丙发生的概率为
C.甲与丁相互独立 D.乙与丙相互独立
二、多项选择题
9.在中,角A,B,C所对的边分别为a,b,c,下列说法中正确的是( )
A.若,则是等腰三角形
B.若,,,则
C.若,,,则
D.若面积为,则
10.某市2023年经过招商引资后,经济收入较前一年增加了一倍,实现翻番,为更好地了解该市的经济收入的变化情况,统计了该市招商引资前后的年经济收入构成比例,得到如下扇形图.则下列结论中正确的是( )
A.招商引资后,工资净收入较前一年减少
B.招商引资后,转移净收入是前一年的2.5倍
C.招商引资后,转移净收入与财产净收入的总和超过了该年经济收入的
D.招商引资后,经营净收入较前一年增加了一倍
11.如图,直四棱柱中,底面是,的矩形,直四棱柱的高为4,E,F分别为棱,的中点,则下列说法中正确的有( )
A.直线与相交
B.异面直线与所成角为
C.二面角的平面角为
D.平面截该长方体所得的截面为五边形
三、填空题
12.已知,,则________.
13.已知互不相等的4个正整数从小到大排序为x,y,z,6.若这4个数据的极差是中位数的2倍,则这4个数据的第75百分位数为________.
14.已知的内角A,B,C所对的边分别是a,b,c,点D是AB的中点.若且,,则________.
四、解答题
15.已知向量与的夹角,且,.
(1)求;
(2)求.
16.某社区为了解志愿者每周志愿服务的时长,在全社区300名志愿者中随机抽取20名志愿者在某个星期的志愿服务记录,统计他们当周在社区的志愿服务时长,按时长分组,得到频率分布直方图如图所示:
(1)求a的值;社区对志愿服务时长大于或等于11小时的志愿者认定为优秀志愿者,如果以当周志愿服务统计结果作为依据,请估计该社区每周获得优秀的志愿者的人数;
(2)求出这20名志愿者当周志愿服务时长的样本众数、中位数、平均数(结果保留一位小数).
17.如图,在三棱锥中,平面,E,F分别为,的中点,且,,.
(1)证明:;
(2)求二面角的余弦值.
18.如图,在平面四边形中,,,,.
(1)证明:;
(2)求面积的最大值;
(3)设E为线段的中点,求的最大值.
19.在某抽奖活动中,初始时的袋子中有3个除颜色外其余都相同的小球,颜色为2白1红.每次随机抽取一个小球后放回.抽奖规则如下:设定抽中红球为中奖,抽中白球为未中奖;若抽到白球,放回后把袋中的一个白色小球替换为红色;若抽到红球,放回后把三个球的颜色重新变为2白1红的初始状态.记第n次抽奖中奖的概率为.
(1)求,,;
(2)若存在实数a,b,c,对任意的不小于4的正整数n,都有,试确定a,b,c的值,并说明理由;
(3)若累计中奖4次及以上可以获得一枚优胜者勋章,则从初始状态下连抽9次获得至少一枚勋章的概率为多少?
参考答案
1.答案:C
解析:根据题意,,
所以z的虚部是3.
故选:C
2.答案:A
解析:产品总数为件,而抽取60件进行检验,
抽样比例为,则应从乙种型号的产品中抽取件,
故选:A
3.答案:D
解析:对于A,当投掷骰子出现结果为1,1,2,5,6时,满足平均数为3,中位数为2,可以出现点数6,故A错误;
对于B,当投掷骰子出现结果为2,2,3,4,6时,满足中位数为3,众数为2,可以出现点数6,故B错误;
对于C,当投掷骰子出现结果为1,2,3,3,6时,满足中位数为3,
平均数为:,
方差为,
可以出现点数6,故C错误;
对于D,若平均数为2,且出现6点,则方差,
则平均数为2,方差为2.4时,一定没有出现点数6,故D正确.
故选:D.
4.答案:A
解析:
.
故选:A
5.答案:B
解析:设圆锥母线长为l,高为h,底面半径为,
则由,得,所以,
所以.
故选:B.
6.答案:A
解析:,,即或,
当时,,,,与的方向相反,成立;
当时,,,,与的方向相同,不成立.
.
故选:A
7.答案:B
解析:根据题意,平面,平面,所以,
又,,平面,所以平面,
将鳖臑补全成长方体,如图,
则此四面体的外接球的半径为,
其外接球的表面积为.
故选:B.
8.答案:C
解析:由题意可知,两点数和为6的所有可能为,,,,,两点数和为7的所有可能为,,,,,,,,,,
对于A选项,甲与乙可以同时发生,故选项A错误;
对于B选项,由上可知错误,故选项B错误;
对于C选项,,故选项C正确;
对于D选项,,故选项D错误.
故选:C.
9.答案:ACD
解析:对于A,因为,由正弦定理可得
,因为三角形内角和定理,得,
由正弦定理得,因此是等腰三角形,A正确;
对于B.由正弦定理得,
则或,B错误;
对于C,由余弦定理得,,解得,C正确;
对于D,因为面积为,又
所以,所以,显然,
则,,,D正确;
故选:ACD.
10.答案:BD
解析:根据题意,可设招商引资前的经济收入为a,则招商引资后的经济收入为;
对于A,由招商引资前后的年经济收入构成比例可知招商引资前的工资收入为,招商引资后的工资收入为,
可知招商引资后,工资净收入较前一年增多,即A错误;
对于B,招商引资前的转移净收入为,招商引资后的工资收入为,
即招商引资后,转移净收入是前一年的2.5倍,可得B正确;
对于C,由招商引资后的年经济收入构成比例可知转移净收入与财产净收入的总和占比为,小于,即C错误;
对于D,招商引资后的经营净收入为,招商引资前的经营净收入为,可得招商引资后,经营净收入较前一年增加了一倍,即D正确.
故选:BD
11.答案:AD
解析:因为且,可得四边形为梯形,
所以与必相交,所以A正确;
由题意,在长方体中,因为平面,
平面,所以,
假设异面直线与所成角是,即,
平面,,
可得平面,而平面,
则,
在长方形中,因为,,
取中点F,可知正方形中,
可得与不垂直,矛盾,
所以异面直线与所成角不是,所以B错误;
由上图可知,又,即,则,
又平面,平面,所以,
,平面,所以平面,
平面,则,则为二面角的平面角,
又,所以不等于,C错误;
点P是棱上一点,且,取的中点M,连接,,,
因为F,P分别是和的中点,所以,
由四边形为平行四边形,所以,
因为平面平面,所以为平面与平面的交线,
,,为截面的边,截面又与平面及相交,
可得截面的两条边,所以截面共有五边形,所以D正确.
故选:AD.
12.答案:
解析:,
故答案为:.
13.答案:/
解析:易知这4个数据的极差为,中位数为,
即可得,所以;
又因为正整数x,y,z互不相等且,可得,,;
由为正数,因此这4个数据的第75百分位数为第三个数和第四个数的平均数,即,则这4个数据的第75百分位数为4.5.
故答案为:4.5
14.答案:
解析:根据题意,,由,即为,
由正弦定理得,
又因为,
所以,
因为,可得,所以
又因为为的一条中线,可得,
所以,
即,解得或(舍).
由余弦定理得.
故答案为:.
15.答案:(1)3;
(2)
解析:(1)因为向量与的夹角,且,,
所以,
;
(2)
.
16.答案:(1)0.050,3
(2)8.0,8.4,8.3
解析:(1)由题意,解得,
因为优秀志愿者的频率为,
所以估计该社区每周获得优秀的志愿者的人数有:人;
(2)由图可知这20名志愿者当周志愿服务时长的样本众数为,
设中位数为x,服务时长在小时的频率为,
服务时长在小时的频率为,
所以,而,解得,
这20名志愿者当周志愿服务时长的样本平均数为.
17.答案:(1)证明见解析;
(2)
解析:(1)E,F分别为,的中点,
,.平面,
.,平面,
平面,平面,.
(2)
根据题意,取的中点M,过M作交于N,连接,,,因为F为中点,M为的中点,则,且,
又,,,平面,
平面,
平面,而平面,,
又,,平面,
所以平面,
平面,,即为二面角的平面角,
所以在中,,,则,
由等面积可得,
所以,则,
即二面角的余弦值为.
18.答案:(1)证明见解析;
(2);
(3)3
解析:(1)由题知,在中,由正弦定理得,
因为,所以,所以,
所以,所以.
(2)在中,,
由余弦定理知:,
所以,所以,
解得,等号当仅当时取等号,
所以,.
(3)在中,设,则,则,
由正弦定理知:,
所以,,
在中,由余弦定理知,
所以
,
所以,等号当仅当时,即当时取等号,所以的最大值等于3.
19.答案:(1),,;
(2),,;
(3)
解析:(1),
,
;
(2)因为每次中奖后袋中的球会回到初始状态,
从初始状态开始,若第一次中奖,此时第n次抽奖中奖的概率为,
从初始状态开始,若第一次未中奖而第二次中奖,
此时第n次抽奖中奖的概率为,
从初始状态开始,若前两次均未中奖,则第三次必中奖,
此时第n次抽奖中奖的概率为,
综上所述,对任意的,,
又,所以,,;
(3)由题意知每抽三次至少有一次中奖,故连抽9次至少中奖3次,
所以只需排除3次中奖的情况即可获得一枚优胜者勋章,
另外,每两次中奖的间隔不能超过三次,每次中奖后袋中的球会回到初始状态,从初始状态开始,抽一次中奖的概率为,
从初始状态开始抽两次,第一次未中奖而第二次中奖的概率为,
从初始状态开始抽三次,前两次均未中奖而第三次中奖的概率为,
用表示第i次,第j次,第k次中奖,其余未中奖,
则三次中奖的所有情况如下:,,,,,,,,,,
故仅三次中奖的概率为
,
所以从初始状态下连抽9次获得至少一枚勋章的概率为.
同课章节目录
