四川省广安市2023-2024学年高一下学期7月期末考试 数学(含解析)
文档属性
| 名称 | 四川省广安市2023-2024学年高一下学期7月期末考试 数学(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-31 00:30:12 | ||
图片预览




文档简介
秘密★启用前
广安市2023—2024学年度下期期末教学质量检测
高一数学试题
本试卷分选择题和非选择题两部分.满分150分,考试时间120分钟.
注意事项:
1.答题前,务必将自己的姓名 座位号和准考证号填写在答题卡规定的位置上.
2.答选择题时,必须使用2B铅笔将答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.
3.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上.
4.所有题目必须在答题卡上作答,在试题卷上答题无效.
5.考试结束后,只将答题卡交回.
第I卷(选择题,共58分)
一 选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.在复平面内,复数所表示的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2.从小到大排列的数据的第三四分位数为( )
A. B.9 C. D.10
3.复数满足,则( )
A. B.
C. D.
4.如图,在梯形中,在上,且,设,则( )
A. B.
C. D.
5.已知表示两条不同直线,表示平面,则( )
A.若,则
B.若,则
C.若,则
D.若,则
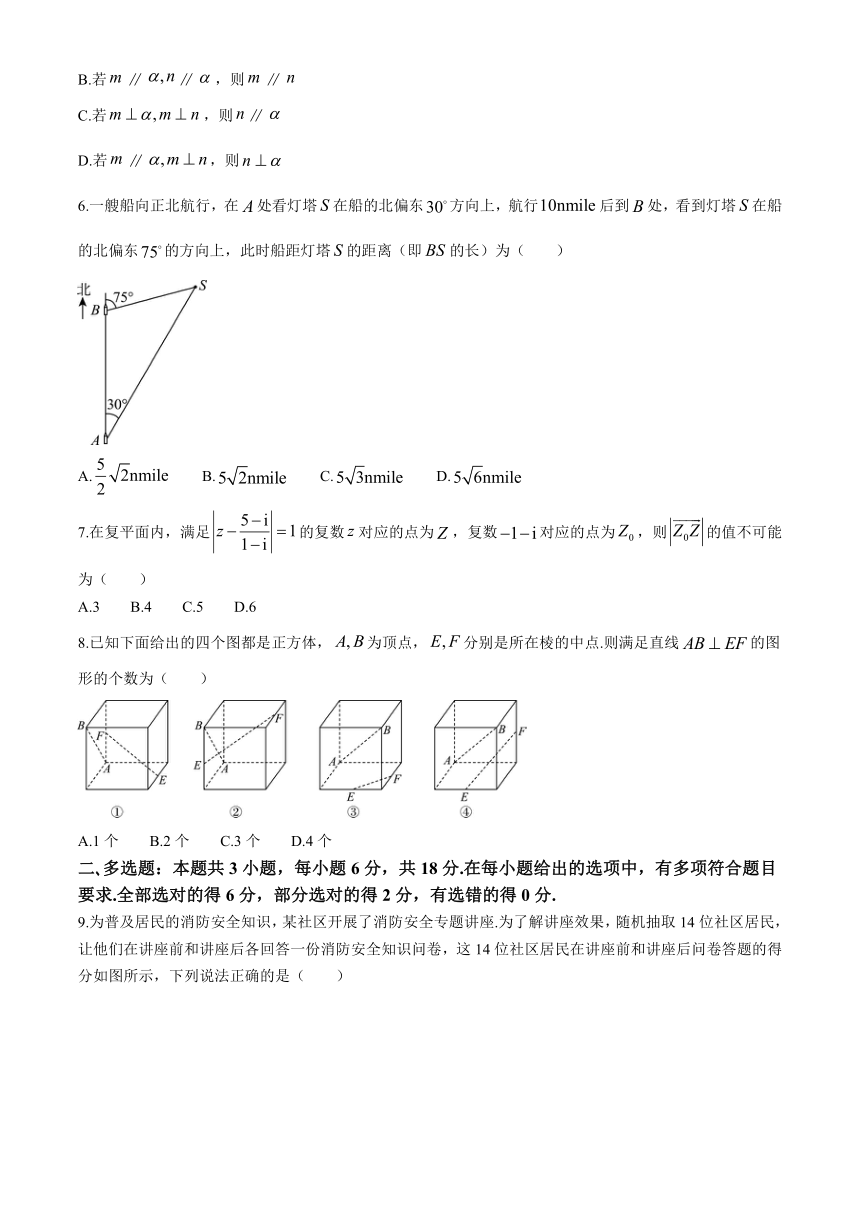
6.一艘船向正北航行,在处看灯塔在船的北偏东方向上,航行后到处,看到灯塔在船的北偏东的方向上,此时船距灯塔的距离(即的长)为( )
A. B. C. D.
7.在复平面内,满足的复数对应的点为,复数对应的点为,则的值不可能为( )
A.3 B.4 C.5 D.6
8.已知下面给出的四个图都是正方体,为顶点,分别是所在棱的中点.则满足直线的图形的个数为( )
A.1个 B.2个 C.3个 D.4个
二 多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得2分,有选错的得0分.
9.为普及居民的消防安全知识,某社区开展了消防安全专题讲座.为了解讲座效果,随机抽取14位社区居民,让他们在讲座前和讲座后各回答一份消防安全知识问卷,这14位社区居民在讲座前和讲座后问卷答题的得分如图所示,下列说法正确的是( )
A.讲座前问卷答题得分的中位数小于70
B.讲座后问卷答题得分的众数为90
C.讲座前问卷答题得分的方差大于讲座后得分的方差
D.讲座前问卷答题得分的极差大于讲座后得分的极差
10.若平面向量满足.则( )
A. B.向量与的夹角为
C. D.在上的投影向量为
11.如图,在棱长为1的正方体中,是的中点,点是侧面上的动点.且平面,则( )
A.在侧面的轨迹长度为
B.异面直线与所成角的最大值为
C.三棱锥的体积为定值
D.直线与平面所成角的正切值的取值范围是
第II卷(非选择题,共92分)
三 填空题:本题共3小题,每小题5分,共15分.
12.某学校高中二年级有男生600人,女生400人,为了解学生的身高情况,现按性别分层,采用比例分配的分层随机抽样方法抽取一个容量为50的样本,则所抽取的男生人数为__________.
13.已知的内角的对边分別为,且边上的高为.则__________.
14.半正多面体亦称“阿基米德多面体”,是由边数不全相同的正多边形围成的多面体.如图是以一个正方体的各条棱的中点为顶点的多面体,这是一个有8个面为正三角形,6个面为正方形的“阿基米德多面体”,包括在内的各个顶点都在球的球面上.若为球上的动点,记三棱锥体积的最大值为,球的体积为.则__________.
四 解答题:本题共5小题,共77分.解答应写出文字说明 证明过程或演算步骤.
15.(13分)
已知复数(其中.
(1)若为实数,求的值;
(2)当时,复数是方程的一个根,求实数的值.
16.(15分)
已知向量.
(1)若与垂直,求实数的值;
(2)已知为平面内四点,且.若三点共线,求实数的值.
17.(15分)
一家水果店为了解本店苹果的日销售情况,记录了过去200天的日销售量(单位:),将全部数据按区间分成5组,得到如图所示的频率分布直方图.
(1)求图中的值;并估计该水果店过去200天苹果日销售量的平均数(同一组中的数据用该组区间的中点值为代表);
(2)若一次进货太多,水果不新鲜;进货太少,又不能满足顾客的需求.店长希望每天的苹果尽量新鲜,又能地满足顾客的需要(在100天中,大约有85天可以满足顾客的需求).请问,每天应该进多少水果?
18.(17分)
从①;②;③.这三个
条件中任选一个补充在下面问题中,并解答该题
记的内角的对边分别为,已知__________.
(1)求角的大小;
(2)若点在上,平分.求的长;
(3)若该三角形为锐角三角形,且面积为,求的取值范围.
注:如果选择多个条件分别解答,那么按第一个解答计分.
19.(17分)
我国古代数学名著《九章算术》在“商功”一章中,将“底面为矩形,一侧棱垂直于底面的四棱锥”称为“阳马”.现有如图所示一个“阳马”形状的几何体,底面是正方形,底面,为线段的中点,为线段上的动点.
(1)平面与平面是否垂直?若垂直,请证明,若不垂直,请说明理由;
(2)求二面角的大小;
(3)若直线平面,求直线与平面所成角的正弦值.
数学试题参考答案及评分标准
一 选择题:本题共8小题,每小题5分,共40分.
1.【命题意图】本小题主要考查复数的代数运算及其几何意义,考查化归与转化等数学思想,考查数学抽象 数学运算等数学核心素养.
【答案】C
【解析】,故所表示的点位于第三象限.
2.【命题意图】本小题主要考查四分位数等基础知识,考查数学抽象等数学核心素养.
【答案】C
【解析】由于,该组数据的第三四分位数为9和10的平均数.
3.【命题意图】本小题主要考查复数的代数运算 共轭复数等基础知识,考查化归与转化等数学思想,考查数学运算等数学核心素养.
【答案】B
【解析】设,则,即,所以且,即,所以.
4.【命题意图】本小题主要考查平面向量的线性运算的几何意义等基础知识,考查数学抽象 直观想象 数学运算等数学核心素养.
【答案】D
【解析】依题意,.
5.【命题意图】本小题主要考查空间直线与平面等基础知识,考查化归与转化 数形结合等数学思想,考查推理论证 空间想象 运算求解等数学能力.
【答案】A
【解析】若,则,故A正确;若,则相交或平行或异面,故B错误;若,则或,故C错误;若,则或或或与相交,故D错误.
6.【命题意图】本小题主要考查正弦定理和余弦定理的应用等基础知识,考查化归与转化 数形结合等数学思想,考查数学抽象 运算求解等数学核心素养.
【答案】B
【解析】在中,,依据正弦定理,,则.
7.【命题意图】本小题主要考查复数运算的几何意义,复数与向量的关系等基础知识,考查化归与转化等数学思想,考查数学抽象 逻辑推理 数学运算等数学核心素养.本小题根据习题7.2第8题内容创编.
【答案】A
【解析】依题意,,点的轨迹为以为圆心,1为半径的圆,故只需求和之间距离的取值范围即可,点到圆心的距离为,则,故的值不可能等于3.
8.【命题意图】本小题主要考查空间直线与平面位置关系等基础知识,考查化归与转化等数学思想,考查空间想象等数学能力.本小题根据第8.6节例2 习题8.6第11题等题创编.
【答案】D
【解析】对于图①和图②,分别取如图所示的棱中点,易证平面,则,故图①和图②均符合题意;对于图③,连接,易证平面,则,图③符合题意;对于图④,取如图所示的棱的中点,易证,于是平面,所以,故图④符合题意.
二 多选题:本题共3小题,每小题6分,共18分.
9.【命题意图】本小题主要考查统计图的识别 统计量的意义等基础知识,考查了数学抽象 数据处理等数学核心素养.
【答案】ACD
【解析】由图可知,讲座前问卷答题的得分的中位数应该小于,A正确;讲座后问卷答题的得分的众数为95,B错误;讲座前问卷答题得分比讲座后波动大,故讲座前问卷答题的得分的方差大于讲座后得分的方差,C正确;由图可知,讲座前问卷答题的得分的极差大于讲座后得分的极差,D正确.
10.【命题意图】本小题主要考查平面向量的线性运算及其几何意义,平面向量的数量积等基础知识,考查化归与转化等数学思想,考查数学抽象 数学运算 直观想象等素养.
【答案】AD
【解析】方法1:由于,则,得正确;,则,C错误;又,所以,则向量与的夹角为,B错误;在上的投影向量为正确.
方法2:根据向量加法的平行四边形法则,满足条件的向量构成如图所示的平行四边形,且,则,A正确;向量与的夹角为错误;,C错误;在上的投影向量为,D正确.
11.【命题意图】本小题主要考查空间直线与平面的位置关系和相关计算,考查推理论证 空间想象 运算求解等数学能力.
【答案】ABD
【解析】如图,取的中点,取的中点,取的中点,依题意,,易证,则,可知,四点共面,又平面平面,所以平面,同理,平面,又平面,所以平面平面,又平面,所以平面,于是,在侧面的轨迹即为线段,由,得,则A正确;
当在处时,此时直线,即异面直线与所成角的最大值为,B正确;由上可知,平面,则线段上的点到平面的距离为定值的面积也为定值,则(定值),C错误;
由于平面平面,故直线与平面所成角和直线与平面所成角相等,取的中点,连接,则平面,故是直线
与平面所成的角,且,易求得,则,D正确.
三 填空题:本题共3小题,每小题5分,共15分.
12.【命题意图】本小题设置课程学习情境,设计抽样问题,主要考查分层抽样方法相关知识;考查运算求解能力,抽象概括能力.本小题源于教材必修第二册“巩固复习”第5题.
【答案】30
【解析】该学校高二年级学生中,男生占比为,则所抽取的男生人数为.
13.【命题意图】本小题主要考查正弦定理和余弦定理的应用,考查化归与转化等数学思想,考查推理论证 运算求解等数学能力.
【答案】3
【解析】依题意得,则,因为,所以的面积,即,根据余弦定理,得,则有,解得.
14.【命题意图】本小题主要考查几何体中的相关运算,体积公式等知识,考查化归与转化等数学思想,考查空间想象 运算求解等数学能力.
【答案】
【解析】根据图形可知,该阿基米德多面体是由一个正方体切去八个角得到的,该多面体的外接球球心与正方体的外接球球心相同,设该多面体的棱长为1,可知球的半径为1,正方体的棱长为为如图正方体中与点等距的一个顶点,设三棱锥的高为,由,得,得,正方体对角线长为,球心到平面距离为,三棱锥的高的最大值为,故其体积的最大值,所以.
四 解答题:本题共5小题,共77分.
15.(13分)
【命题意图】本小题设置课程学习情境,主要考查复数的概念及代数运算等基础知识,考查化归与转化等数学思想,考查数学抽象 数学运算等数学核心素养.
【解析】(1),
因为为实数,
所以,解得.
故为实数时,的值为.
(2)当时,,
则复数,
因为是方程的一个根,
所以,
化简得,
由解得
16.(15分)
【命题意图】本小题设置课程学习情境,主要考查平面向量线性运算 数量积 共线向量及其坐标运算等基础知识,考查化归与转化等数学思想,考查数学抽象 数学运算等数学核心素养.
【解析】(1),
则,
因为与垂直,所以,
解得.
(2),
,
,
,
因为三点共线,所以.
所以,
解得.
17.(15分)
【命题意图】本小题设置生活实践情景,设计水果进货规划问题,考查平均数 百分位数等统计量的计算,样本估计总体,决策等相关知识;考查统计概率思想;运算求解能力和应用能力.本小题源于教材必修第二册P223复习参考题“综合运用”第9题编制.
【解析】(1)由直方图可得,
样本落在的频率分别为,由,
解得.
则样本落在频率分别为,
所以,该苹果日销售量的平均值为
.
(2)为了能地满足顾客的需要,即估计该店苹果日销售量的分位数.
方法1:依题意,日销售量不超过90kg的频率为,
则该店苹果日销售量的分位数在,设为,
则,
解得.
所以,每天应该进95kg苹果.
方法2:依题意,日销售量不超过90kg的频率为,
则该店苹果日销售量的分位数在,
所以日销售量的分位数为.
所以,每天应该进95kg苹果.
18.(17分)
【命题意图】本小题主要考查正弦定和余弦定理等基础知识,考查化归与转化等数学思想,考查推理论证 运算求解等数学能力.
【解析】(1)若选条件①,
依题意,得,根据正弦定理得,
因为,所以,则,即,
即,所以.
又,则,
所以.
若选条件②.
由正弦定理得,
所以
,
即,
即,整理得,即.
因为,所以,
所以.
若选条件③
在中,因为,
所以,
即,
化简得.
又,则,故.
因为,所以.
(2)依题意,,
即,则,
在中,根据余弦定理,
有,
即,解得或(舍去),
所以.
(3)依题意,的面积,所以.
又为锐角三角形,且,
则,所以.
又,则,所以.
由正弦定理,得,
所以
,
所以,即,
所以的取值范围为.
19.(17分)
【命题意图】本小题设置探索创新情境,设计空间直线 平面的位置关系问题,主要考查直线与平面的位置关系 直线与平面所成角 二面角等基础知识;考查直观想象 逻辑推理 数学运算等数学核心素养.本小题源于教材必修第二册P164习题8.6“拓展探索”第21题.
【解析】(1)平面平面.
理由如下:
因为平面平面,
所以,
因为,又.
所以平面,故.
在中,为的中点,所以.
因为平面平面,
所以平面.又平面,
所以平面平面.
(2)不妨设,计算可得,
又,
所以,
则,作于,连结,又,
可知,所以,
所以是二面角的平面角
在中,由,
得,则,
连结,知,在中,根据余弦定理,
得
,
所以.
(3)因为直线平面平面,平面平面,
所以直线直线.
又为线段的中点,所以为线段上的中点.
由(2)知,所以.
设与交点为,连结,
由(1)知,平面平面,平面平面,
所以平面.
所以直线与平面所成角为.
又由为上的中点,可得为的中点,
可知,,又,
所以.
直线与平面所成角的正弦值为.
广安市2023—2024学年度下期期末教学质量检测
高一数学试题
本试卷分选择题和非选择题两部分.满分150分,考试时间120分钟.
注意事项:
1.答题前,务必将自己的姓名 座位号和准考证号填写在答题卡规定的位置上.
2.答选择题时,必须使用2B铅笔将答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.
3.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上.
4.所有题目必须在答题卡上作答,在试题卷上答题无效.
5.考试结束后,只将答题卡交回.
第I卷(选择题,共58分)
一 选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.在复平面内,复数所表示的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2.从小到大排列的数据的第三四分位数为( )
A. B.9 C. D.10
3.复数满足,则( )
A. B.
C. D.
4.如图,在梯形中,在上,且,设,则( )
A. B.
C. D.
5.已知表示两条不同直线,表示平面,则( )
A.若,则
B.若,则
C.若,则
D.若,则
6.一艘船向正北航行,在处看灯塔在船的北偏东方向上,航行后到处,看到灯塔在船的北偏东的方向上,此时船距灯塔的距离(即的长)为( )
A. B. C. D.
7.在复平面内,满足的复数对应的点为,复数对应的点为,则的值不可能为( )
A.3 B.4 C.5 D.6
8.已知下面给出的四个图都是正方体,为顶点,分别是所在棱的中点.则满足直线的图形的个数为( )
A.1个 B.2个 C.3个 D.4个
二 多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得2分,有选错的得0分.
9.为普及居民的消防安全知识,某社区开展了消防安全专题讲座.为了解讲座效果,随机抽取14位社区居民,让他们在讲座前和讲座后各回答一份消防安全知识问卷,这14位社区居民在讲座前和讲座后问卷答题的得分如图所示,下列说法正确的是( )
A.讲座前问卷答题得分的中位数小于70
B.讲座后问卷答题得分的众数为90
C.讲座前问卷答题得分的方差大于讲座后得分的方差
D.讲座前问卷答题得分的极差大于讲座后得分的极差
10.若平面向量满足.则( )
A. B.向量与的夹角为
C. D.在上的投影向量为
11.如图,在棱长为1的正方体中,是的中点,点是侧面上的动点.且平面,则( )
A.在侧面的轨迹长度为
B.异面直线与所成角的最大值为
C.三棱锥的体积为定值
D.直线与平面所成角的正切值的取值范围是
第II卷(非选择题,共92分)
三 填空题:本题共3小题,每小题5分,共15分.
12.某学校高中二年级有男生600人,女生400人,为了解学生的身高情况,现按性别分层,采用比例分配的分层随机抽样方法抽取一个容量为50的样本,则所抽取的男生人数为__________.
13.已知的内角的对边分別为,且边上的高为.则__________.
14.半正多面体亦称“阿基米德多面体”,是由边数不全相同的正多边形围成的多面体.如图是以一个正方体的各条棱的中点为顶点的多面体,这是一个有8个面为正三角形,6个面为正方形的“阿基米德多面体”,包括在内的各个顶点都在球的球面上.若为球上的动点,记三棱锥体积的最大值为,球的体积为.则__________.
四 解答题:本题共5小题,共77分.解答应写出文字说明 证明过程或演算步骤.
15.(13分)
已知复数(其中.
(1)若为实数,求的值;
(2)当时,复数是方程的一个根,求实数的值.
16.(15分)
已知向量.
(1)若与垂直,求实数的值;
(2)已知为平面内四点,且.若三点共线,求实数的值.
17.(15分)
一家水果店为了解本店苹果的日销售情况,记录了过去200天的日销售量(单位:),将全部数据按区间分成5组,得到如图所示的频率分布直方图.
(1)求图中的值;并估计该水果店过去200天苹果日销售量的平均数(同一组中的数据用该组区间的中点值为代表);
(2)若一次进货太多,水果不新鲜;进货太少,又不能满足顾客的需求.店长希望每天的苹果尽量新鲜,又能地满足顾客的需要(在100天中,大约有85天可以满足顾客的需求).请问,每天应该进多少水果?
18.(17分)
从①;②;③.这三个
条件中任选一个补充在下面问题中,并解答该题
记的内角的对边分别为,已知__________.
(1)求角的大小;
(2)若点在上,平分.求的长;
(3)若该三角形为锐角三角形,且面积为,求的取值范围.
注:如果选择多个条件分别解答,那么按第一个解答计分.
19.(17分)
我国古代数学名著《九章算术》在“商功”一章中,将“底面为矩形,一侧棱垂直于底面的四棱锥”称为“阳马”.现有如图所示一个“阳马”形状的几何体,底面是正方形,底面,为线段的中点,为线段上的动点.
(1)平面与平面是否垂直?若垂直,请证明,若不垂直,请说明理由;
(2)求二面角的大小;
(3)若直线平面,求直线与平面所成角的正弦值.
数学试题参考答案及评分标准
一 选择题:本题共8小题,每小题5分,共40分.
1.【命题意图】本小题主要考查复数的代数运算及其几何意义,考查化归与转化等数学思想,考查数学抽象 数学运算等数学核心素养.
【答案】C
【解析】,故所表示的点位于第三象限.
2.【命题意图】本小题主要考查四分位数等基础知识,考查数学抽象等数学核心素养.
【答案】C
【解析】由于,该组数据的第三四分位数为9和10的平均数.
3.【命题意图】本小题主要考查复数的代数运算 共轭复数等基础知识,考查化归与转化等数学思想,考查数学运算等数学核心素养.
【答案】B
【解析】设,则,即,所以且,即,所以.
4.【命题意图】本小题主要考查平面向量的线性运算的几何意义等基础知识,考查数学抽象 直观想象 数学运算等数学核心素养.
【答案】D
【解析】依题意,.
5.【命题意图】本小题主要考查空间直线与平面等基础知识,考查化归与转化 数形结合等数学思想,考查推理论证 空间想象 运算求解等数学能力.
【答案】A
【解析】若,则,故A正确;若,则相交或平行或异面,故B错误;若,则或,故C错误;若,则或或或与相交,故D错误.
6.【命题意图】本小题主要考查正弦定理和余弦定理的应用等基础知识,考查化归与转化 数形结合等数学思想,考查数学抽象 运算求解等数学核心素养.
【答案】B
【解析】在中,,依据正弦定理,,则.
7.【命题意图】本小题主要考查复数运算的几何意义,复数与向量的关系等基础知识,考查化归与转化等数学思想,考查数学抽象 逻辑推理 数学运算等数学核心素养.本小题根据习题7.2第8题内容创编.
【答案】A
【解析】依题意,,点的轨迹为以为圆心,1为半径的圆,故只需求和之间距离的取值范围即可,点到圆心的距离为,则,故的值不可能等于3.
8.【命题意图】本小题主要考查空间直线与平面位置关系等基础知识,考查化归与转化等数学思想,考查空间想象等数学能力.本小题根据第8.6节例2 习题8.6第11题等题创编.
【答案】D
【解析】对于图①和图②,分别取如图所示的棱中点,易证平面,则,故图①和图②均符合题意;对于图③,连接,易证平面,则,图③符合题意;对于图④,取如图所示的棱的中点,易证,于是平面,所以,故图④符合题意.
二 多选题:本题共3小题,每小题6分,共18分.
9.【命题意图】本小题主要考查统计图的识别 统计量的意义等基础知识,考查了数学抽象 数据处理等数学核心素养.
【答案】ACD
【解析】由图可知,讲座前问卷答题的得分的中位数应该小于,A正确;讲座后问卷答题的得分的众数为95,B错误;讲座前问卷答题得分比讲座后波动大,故讲座前问卷答题的得分的方差大于讲座后得分的方差,C正确;由图可知,讲座前问卷答题的得分的极差大于讲座后得分的极差,D正确.
10.【命题意图】本小题主要考查平面向量的线性运算及其几何意义,平面向量的数量积等基础知识,考查化归与转化等数学思想,考查数学抽象 数学运算 直观想象等素养.
【答案】AD
【解析】方法1:由于,则,得正确;,则,C错误;又,所以,则向量与的夹角为,B错误;在上的投影向量为正确.
方法2:根据向量加法的平行四边形法则,满足条件的向量构成如图所示的平行四边形,且,则,A正确;向量与的夹角为错误;,C错误;在上的投影向量为,D正确.
11.【命题意图】本小题主要考查空间直线与平面的位置关系和相关计算,考查推理论证 空间想象 运算求解等数学能力.
【答案】ABD
【解析】如图,取的中点,取的中点,取的中点,依题意,,易证,则,可知,四点共面,又平面平面,所以平面,同理,平面,又平面,所以平面平面,又平面,所以平面,于是,在侧面的轨迹即为线段,由,得,则A正确;
当在处时,此时直线,即异面直线与所成角的最大值为,B正确;由上可知,平面,则线段上的点到平面的距离为定值的面积也为定值,则(定值),C错误;
由于平面平面,故直线与平面所成角和直线与平面所成角相等,取的中点,连接,则平面,故是直线
与平面所成的角,且,易求得,则,D正确.
三 填空题:本题共3小题,每小题5分,共15分.
12.【命题意图】本小题设置课程学习情境,设计抽样问题,主要考查分层抽样方法相关知识;考查运算求解能力,抽象概括能力.本小题源于教材必修第二册“巩固复习”第5题.
【答案】30
【解析】该学校高二年级学生中,男生占比为,则所抽取的男生人数为.
13.【命题意图】本小题主要考查正弦定理和余弦定理的应用,考查化归与转化等数学思想,考查推理论证 运算求解等数学能力.
【答案】3
【解析】依题意得,则,因为,所以的面积,即,根据余弦定理,得,则有,解得.
14.【命题意图】本小题主要考查几何体中的相关运算,体积公式等知识,考查化归与转化等数学思想,考查空间想象 运算求解等数学能力.
【答案】
【解析】根据图形可知,该阿基米德多面体是由一个正方体切去八个角得到的,该多面体的外接球球心与正方体的外接球球心相同,设该多面体的棱长为1,可知球的半径为1,正方体的棱长为为如图正方体中与点等距的一个顶点,设三棱锥的高为,由,得,得,正方体对角线长为,球心到平面距离为,三棱锥的高的最大值为,故其体积的最大值,所以.
四 解答题:本题共5小题,共77分.
15.(13分)
【命题意图】本小题设置课程学习情境,主要考查复数的概念及代数运算等基础知识,考查化归与转化等数学思想,考查数学抽象 数学运算等数学核心素养.
【解析】(1),
因为为实数,
所以,解得.
故为实数时,的值为.
(2)当时,,
则复数,
因为是方程的一个根,
所以,
化简得,
由解得
16.(15分)
【命题意图】本小题设置课程学习情境,主要考查平面向量线性运算 数量积 共线向量及其坐标运算等基础知识,考查化归与转化等数学思想,考查数学抽象 数学运算等数学核心素养.
【解析】(1),
则,
因为与垂直,所以,
解得.
(2),
,
,
,
因为三点共线,所以.
所以,
解得.
17.(15分)
【命题意图】本小题设置生活实践情景,设计水果进货规划问题,考查平均数 百分位数等统计量的计算,样本估计总体,决策等相关知识;考查统计概率思想;运算求解能力和应用能力.本小题源于教材必修第二册P223复习参考题“综合运用”第9题编制.
【解析】(1)由直方图可得,
样本落在的频率分别为,由,
解得.
则样本落在频率分别为,
所以,该苹果日销售量的平均值为
.
(2)为了能地满足顾客的需要,即估计该店苹果日销售量的分位数.
方法1:依题意,日销售量不超过90kg的频率为,
则该店苹果日销售量的分位数在,设为,
则,
解得.
所以,每天应该进95kg苹果.
方法2:依题意,日销售量不超过90kg的频率为,
则该店苹果日销售量的分位数在,
所以日销售量的分位数为.
所以,每天应该进95kg苹果.
18.(17分)
【命题意图】本小题主要考查正弦定和余弦定理等基础知识,考查化归与转化等数学思想,考查推理论证 运算求解等数学能力.
【解析】(1)若选条件①,
依题意,得,根据正弦定理得,
因为,所以,则,即,
即,所以.
又,则,
所以.
若选条件②.
由正弦定理得,
所以
,
即,
即,整理得,即.
因为,所以,
所以.
若选条件③
在中,因为,
所以,
即,
化简得.
又,则,故.
因为,所以.
(2)依题意,,
即,则,
在中,根据余弦定理,
有,
即,解得或(舍去),
所以.
(3)依题意,的面积,所以.
又为锐角三角形,且,
则,所以.
又,则,所以.
由正弦定理,得,
所以
,
所以,即,
所以的取值范围为.
19.(17分)
【命题意图】本小题设置探索创新情境,设计空间直线 平面的位置关系问题,主要考查直线与平面的位置关系 直线与平面所成角 二面角等基础知识;考查直观想象 逻辑推理 数学运算等数学核心素养.本小题源于教材必修第二册P164习题8.6“拓展探索”第21题.
【解析】(1)平面平面.
理由如下:
因为平面平面,
所以,
因为,又.
所以平面,故.
在中,为的中点,所以.
因为平面平面,
所以平面.又平面,
所以平面平面.
(2)不妨设,计算可得,
又,
所以,
则,作于,连结,又,
可知,所以,
所以是二面角的平面角
在中,由,
得,则,
连结,知,在中,根据余弦定理,
得
,
所以.
(3)因为直线平面平面,平面平面,
所以直线直线.
又为线段的中点,所以为线段上的中点.
由(2)知,所以.
设与交点为,连结,
由(1)知,平面平面,平面平面,
所以平面.
所以直线与平面所成角为.
又由为上的中点,可得为的中点,
可知,,又,
所以.
直线与平面所成角的正弦值为.
同课章节目录
