11.2.2 三角形的外角 同步练习 (含答案)2024—2025学年人教版数学八年级上册
文档属性
| 名称 | 11.2.2 三角形的外角 同步练习 (含答案)2024—2025学年人教版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 524.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-31 06:03:17 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
11.2.2 三角形的外角
A层
知识点 三角形外角的性质
1.如图,∠A=40°,∠CBD 是△ABC 的外角,∠CBD =120°,则∠C 的大小是 ( )
A.90° B.80° C.60° D.40°
2.如图,已知直线l 、l 、l 两两相交,且l ⊥l .若α=50°,则β的度数为( )
A.120° B.130° C.140° D.150°
3.如图,下列结论正确的是 ( )
A.∠1>∠2>∠A B.∠1>∠A>∠2
C.∠A>∠2>∠1 D.∠2>∠1>∠A
4.如图,∠A = 20°,∠B =30°,∠C=50°,则∠ADB 的度数为 .
5.如图,在△ABC 中,∠ADB =100°,∠C =80°, BE 平分∠ABC,求∠BED的度数.
A
B层
6.如图,在Rt△ADB 中,∠D=90°,C 为AD 上一点,∠ACB=6x,则x 的值可以是 ( )
A.10° B.20° C.30° D.40°
7.如图,在 △ABC 中,∠A = 50°, BE 平 分∠ABC,CE 平分∠ACD,则∠E 的度数为( )
A.25° B.30° C.50° D.45°
8.若一个三角形有两个外角的和等于 270°,则此三角形一定是 三角形(填“锐角”“直角”或“钝角”).
9.小明把一副含 45°,30°角的直角三角板如图摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于 .
10.如图,∠B=30°,∠C=10°,AE、DE 分别平分∠BAC 和∠BDC.
(1)如图①,求∠E 的度数;
(2)如图②,求∠E 的度数.
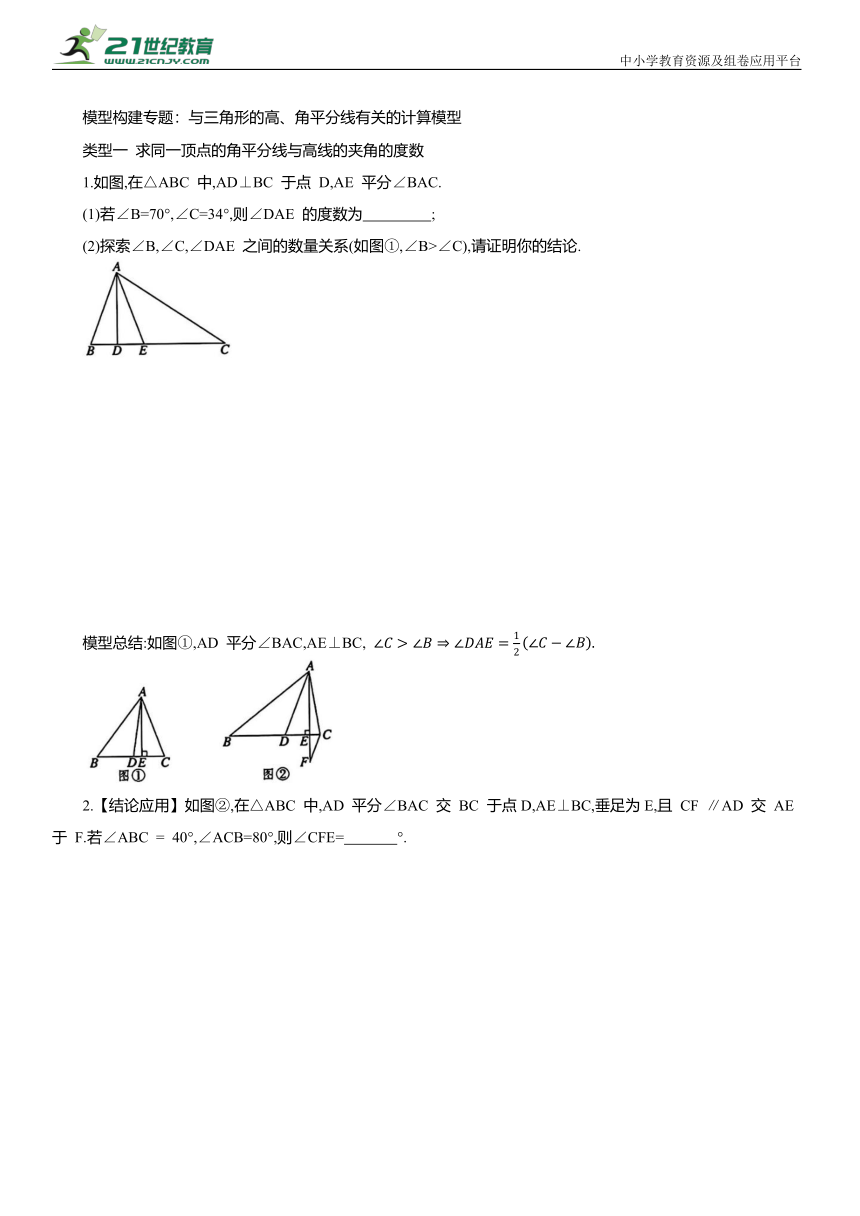
模型构建专题:与三角形的高、角平分线有关的计算模型
类型一 求同一顶点的角平分线与高线的夹角的度数
1.如图,在△ABC 中,AD⊥BC 于点 D,AE 平分∠BAC.
(1)若∠B=70°,∠C=34°,则∠DAE 的度数为 ;
(2)探索∠B,∠C,∠DAE 之间的数量关系(如图①,∠B>∠C),请证明你的结论.
模型总结:如图①,AD 平分∠BAC,AE⊥BC,
2.【结论应用】如图②,在△ABC 中,AD 平分∠BAC 交 BC 于点D,AE⊥BC,垂足为E,且 CF ∥AD 交 AE 于 F.若∠ABC = 40°,∠ACB=80°,则∠CFE= °.
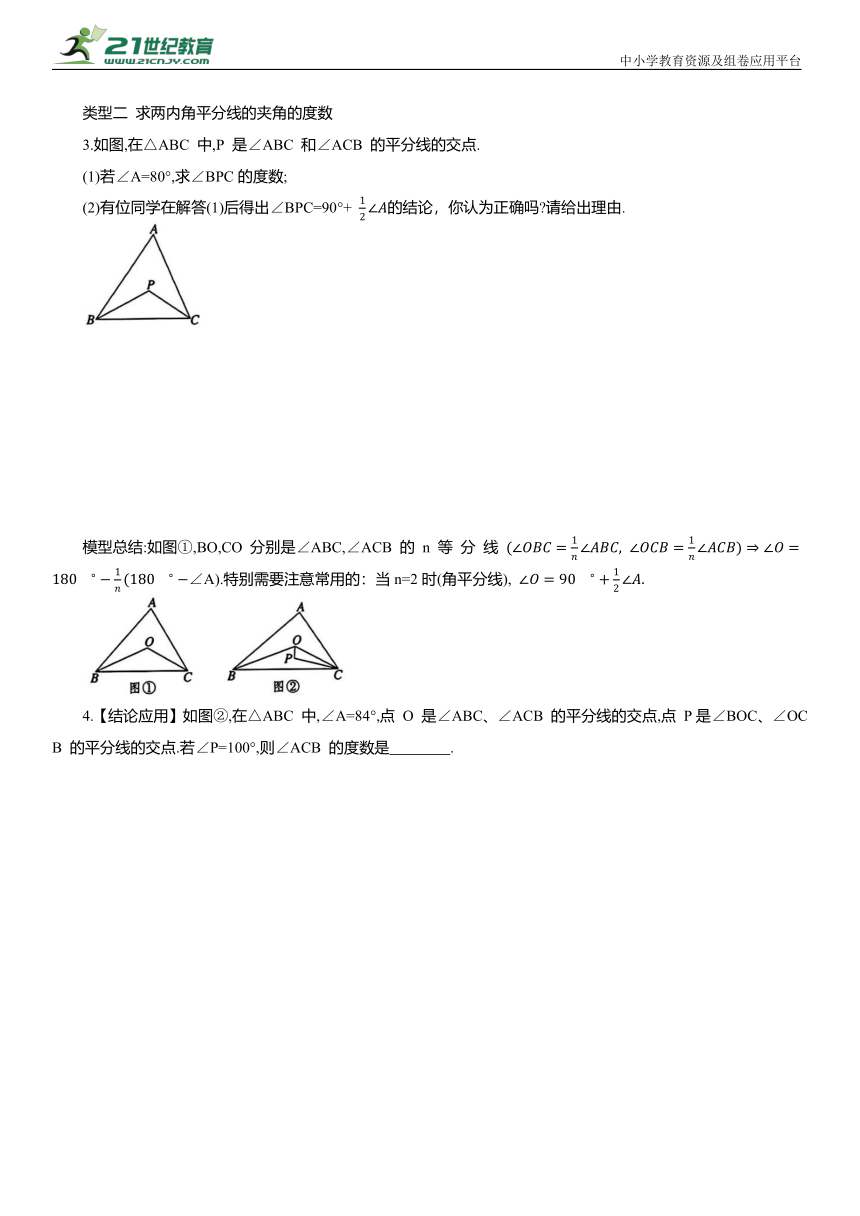
类型二 求两内角平分线的夹角的度数
3.如图,在△ABC 中,P 是∠ABC 和∠ACB 的平分线的交点.
(1)若∠A=80°,求∠BPC的度数;
(2)有位同学在解答(1)后得出∠BPC=90°+ 的结论,你认为正确吗 请给出理由.
模型总结:如图①,BO,CO 分别是∠ABC,∠ACB 的 n 等 分 线 ∠A).特别需要注意常用的:当n=2时(角平分线),
4.【结论应用】如图②,在△ABC 中,∠A=84°,点 O 是∠ABC、∠ACB 的平分线的交点,点 P是∠BOC、∠OCB 的平分线的交点.若∠P=100°,则∠ACB 的度数是 .
类型三 求一内角平分线与一外角平分线的夹角的度数
5.如图,在△ABC 中,BA 平分∠ABC,CA 平分∠ACD.
(1)求证:
(2)如图,继续作∠A BC 和∠A CD 的平分线交 于 点 A ,得 ∠A ; 作 ∠A BC 和∠A CD 的平分线交于点A ,得∠A ……作∠A2018BC 和∠A2018CD 的平分线交于点A ,得∠A .若∠A=α,则∠A = (用含α的式子表示).
模型总结:如图①,BO,CO,BO',CO'分别为∠ABC,∠ACD,∠OBC,∠OCD 的平分线
6.如图②,△ABC中,∠A = 50°,BP,CP,BM,CM 分别是∠ABC,∠ACD,∠PBC,∠PCB 的平分线,则∠M 的度数为 .
7.【结论应用】如图,在△ABC 中,点 D是 AC 延长线上的一点,过点 D 作DE∥BC,DF 平分∠ADE,BF 平分∠ABC.设∠A=n°,则∠F 的度数为 (用含 n 的式子表示).
类型四 求两外角平分线的夹角的度数
8.(1)如图,BO 平分△ABC 的外角∠CBD,CO平分△ABC 的外角∠BCE,则∠BOC 与∠A 的关系为 ;
(2)请就(1)中的结论进行证明.
模型总结:如图①,BO,CO 分别为∠CBD,∠BCE 的平分线==
9.【结论应用】如图②,点O 是△ABC 内角平分线的交点,点 I 是△ABC 外角平分线的交点,则∠O 与∠I 的数量关系是 .
11.2.2 三角形的外角
1. B 2. C 3. A 4.100°
5.解:∵∠ADB=100°,∠C=80°,∴∠DAC=∠ADB ∠C= 100° 80° = 20°. 在△ABD 中,∠ABC = 180°— ∵BE 平分. ×70°=35°.∴∠BED=∠BAD+∠ABE=
6. B 7. A 8.直角 9.210°
10.解:∵AE、DE 分别平分∠BAC 和∠BDC,∴ 可 以 假 设 ∠EDC = ∠EDB = x,∠EAC=∠EAB=y.
(1)由题意得 可 得
(2)延长 ED 交 AC 于 F,则∠CDE =∠C+∠CFD,∠CFD=∠CAE+∠E.由题 意 得 可 得 ∠E =
模型构建专题:与三角形的高、
角平分线有关的计算模型
1.解:(1)18°
证 明: ∵∠BAC = 180°— ∠B — ∠C, AE 平 分 BC,∴∠ADC=90°.∴∠CAD=90°-∠C.∴∠DAE=∠DAC-∠EAC=90°-∠C-
2.20
3.解:(1)∵BP 平分∠ABC,CP 平分∠ACB,
(2)正确.理由如下:∵BP 平分∠ABC,CP平 分 ∠ACB, ∴∠PBC + ∠PCB =
4.56°
5.(1)证明:∵CA 平分∠ACD,∴∠A CD= 又∵∠A CD=∠A + ∠A BC, ∴ ∠A + ∠A BC = 平 分 ∠ABC,
6.102.5°
解题思路:延长 BC,过点 C 作 CG∥DF,交 BF 于点G.则 CG 平分△ABC 的外角∠ACH.则.
8.解: (2)证明如下:如图,∵BO,CO 分别是△ABC 的外角∠DBC,∠ECB 的平分线,∴∠DBC=2∠1=∠ACB+∠A,∠ECB=2∠2=∠ABC+∠A.∴2∠1+2∠2=∠A+∠A+∠ABC+∠ACB=∠A+ 又∵∠1+∠2+∠BOC=180°,∴∠BOC=180°-(∠1+∠2)=
9.∠O+∠I=180°
11.2.2 三角形的外角
A层
知识点 三角形外角的性质
1.如图,∠A=40°,∠CBD 是△ABC 的外角,∠CBD =120°,则∠C 的大小是 ( )
A.90° B.80° C.60° D.40°
2.如图,已知直线l 、l 、l 两两相交,且l ⊥l .若α=50°,则β的度数为( )
A.120° B.130° C.140° D.150°
3.如图,下列结论正确的是 ( )
A.∠1>∠2>∠A B.∠1>∠A>∠2
C.∠A>∠2>∠1 D.∠2>∠1>∠A
4.如图,∠A = 20°,∠B =30°,∠C=50°,则∠ADB 的度数为 .
5.如图,在△ABC 中,∠ADB =100°,∠C =80°, BE 平分∠ABC,求∠BED的度数.
A
B层
6.如图,在Rt△ADB 中,∠D=90°,C 为AD 上一点,∠ACB=6x,则x 的值可以是 ( )
A.10° B.20° C.30° D.40°
7.如图,在 △ABC 中,∠A = 50°, BE 平 分∠ABC,CE 平分∠ACD,则∠E 的度数为( )
A.25° B.30° C.50° D.45°
8.若一个三角形有两个外角的和等于 270°,则此三角形一定是 三角形(填“锐角”“直角”或“钝角”).
9.小明把一副含 45°,30°角的直角三角板如图摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于 .
10.如图,∠B=30°,∠C=10°,AE、DE 分别平分∠BAC 和∠BDC.
(1)如图①,求∠E 的度数;
(2)如图②,求∠E 的度数.
模型构建专题:与三角形的高、角平分线有关的计算模型
类型一 求同一顶点的角平分线与高线的夹角的度数
1.如图,在△ABC 中,AD⊥BC 于点 D,AE 平分∠BAC.
(1)若∠B=70°,∠C=34°,则∠DAE 的度数为 ;
(2)探索∠B,∠C,∠DAE 之间的数量关系(如图①,∠B>∠C),请证明你的结论.
模型总结:如图①,AD 平分∠BAC,AE⊥BC,
2.【结论应用】如图②,在△ABC 中,AD 平分∠BAC 交 BC 于点D,AE⊥BC,垂足为E,且 CF ∥AD 交 AE 于 F.若∠ABC = 40°,∠ACB=80°,则∠CFE= °.
类型二 求两内角平分线的夹角的度数
3.如图,在△ABC 中,P 是∠ABC 和∠ACB 的平分线的交点.
(1)若∠A=80°,求∠BPC的度数;
(2)有位同学在解答(1)后得出∠BPC=90°+ 的结论,你认为正确吗 请给出理由.
模型总结:如图①,BO,CO 分别是∠ABC,∠ACB 的 n 等 分 线 ∠A).特别需要注意常用的:当n=2时(角平分线),
4.【结论应用】如图②,在△ABC 中,∠A=84°,点 O 是∠ABC、∠ACB 的平分线的交点,点 P是∠BOC、∠OCB 的平分线的交点.若∠P=100°,则∠ACB 的度数是 .
类型三 求一内角平分线与一外角平分线的夹角的度数
5.如图,在△ABC 中,BA 平分∠ABC,CA 平分∠ACD.
(1)求证:
(2)如图,继续作∠A BC 和∠A CD 的平分线交 于 点 A ,得 ∠A ; 作 ∠A BC 和∠A CD 的平分线交于点A ,得∠A ……作∠A2018BC 和∠A2018CD 的平分线交于点A ,得∠A .若∠A=α,则∠A = (用含α的式子表示).
模型总结:如图①,BO,CO,BO',CO'分别为∠ABC,∠ACD,∠OBC,∠OCD 的平分线
6.如图②,△ABC中,∠A = 50°,BP,CP,BM,CM 分别是∠ABC,∠ACD,∠PBC,∠PCB 的平分线,则∠M 的度数为 .
7.【结论应用】如图,在△ABC 中,点 D是 AC 延长线上的一点,过点 D 作DE∥BC,DF 平分∠ADE,BF 平分∠ABC.设∠A=n°,则∠F 的度数为 (用含 n 的式子表示).
类型四 求两外角平分线的夹角的度数
8.(1)如图,BO 平分△ABC 的外角∠CBD,CO平分△ABC 的外角∠BCE,则∠BOC 与∠A 的关系为 ;
(2)请就(1)中的结论进行证明.
模型总结:如图①,BO,CO 分别为∠CBD,∠BCE 的平分线==
9.【结论应用】如图②,点O 是△ABC 内角平分线的交点,点 I 是△ABC 外角平分线的交点,则∠O 与∠I 的数量关系是 .
11.2.2 三角形的外角
1. B 2. C 3. A 4.100°
5.解:∵∠ADB=100°,∠C=80°,∴∠DAC=∠ADB ∠C= 100° 80° = 20°. 在△ABD 中,∠ABC = 180°— ∵BE 平分. ×70°=35°.∴∠BED=∠BAD+∠ABE=
6. B 7. A 8.直角 9.210°
10.解:∵AE、DE 分别平分∠BAC 和∠BDC,∴ 可 以 假 设 ∠EDC = ∠EDB = x,∠EAC=∠EAB=y.
(1)由题意得 可 得
(2)延长 ED 交 AC 于 F,则∠CDE =∠C+∠CFD,∠CFD=∠CAE+∠E.由题 意 得 可 得 ∠E =
模型构建专题:与三角形的高、
角平分线有关的计算模型
1.解:(1)18°
证 明: ∵∠BAC = 180°— ∠B — ∠C, AE 平 分 BC,∴∠ADC=90°.∴∠CAD=90°-∠C.∴∠DAE=∠DAC-∠EAC=90°-∠C-
2.20
3.解:(1)∵BP 平分∠ABC,CP 平分∠ACB,
(2)正确.理由如下:∵BP 平分∠ABC,CP平 分 ∠ACB, ∴∠PBC + ∠PCB =
4.56°
5.(1)证明:∵CA 平分∠ACD,∴∠A CD= 又∵∠A CD=∠A + ∠A BC, ∴ ∠A + ∠A BC = 平 分 ∠ABC,
6.102.5°
解题思路:延长 BC,过点 C 作 CG∥DF,交 BF 于点G.则 CG 平分△ABC 的外角∠ACH.则.
8.解: (2)证明如下:如图,∵BO,CO 分别是△ABC 的外角∠DBC,∠ECB 的平分线,∴∠DBC=2∠1=∠ACB+∠A,∠ECB=2∠2=∠ABC+∠A.∴2∠1+2∠2=∠A+∠A+∠ABC+∠ACB=∠A+ 又∵∠1+∠2+∠BOC=180°,∴∠BOC=180°-(∠1+∠2)=
9.∠O+∠I=180°
