第 4 课时 “斜边、直角边” 同步练习 (含答案)2024—2025学年人教版数学八年级上册
文档属性
| 名称 | 第 4 课时 “斜边、直角边” 同步练习 (含答案)2024—2025学年人教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 498.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-31 06:11:42 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第 4 课时 “斜边、直角边”
A层
知识点一 直角三角形全等的判定(“斜边、直角边”)
1.如图,已知 AC⊥BD,垂足为点 O,若 AO=CO,AB=CD,则 Rt△AOB≌Rt△COD,理由是 ( )
A. HL B. SAS C. ASA D. AAS
2.如图,BE=CF,AE⊥BC,DF⊥BC,垂足分别为点 E,F,要根据“HL”证明 Rt△ABE≌Rt△DCF,则还需要添加的一个条件是 ( )
A. AE=DF B.∠A=∠D
C.∠B=∠C D. AB=DC
3.如图,在四边形ABCD 中,CD=CB,∠B=∠D=90°,∠BAC=55°,则∠BCD 的度数为
4.如图,已知∠C=∠D=90°,BC 与AD 交于点E,AC=BD.求证:AD=BC.
知识点二 直角三角形全等的综合判定
5.下列条件中,不能判定两个直角三角形全等的是 ( )
A.斜边和一直角边对应相等
B.两个锐角对应相等
C.一锐角和斜边对应相等
D.两条直角边对应相等
6.如图,AC⊥BD 于 P,AP=CP,增加下列一个条件:①BP=DP;②AB=CD;③∠A=∠C.其中能判定△ABP≌△CDP 的条件有 ( )
A.0个 B.1个 C.2个 D.3个
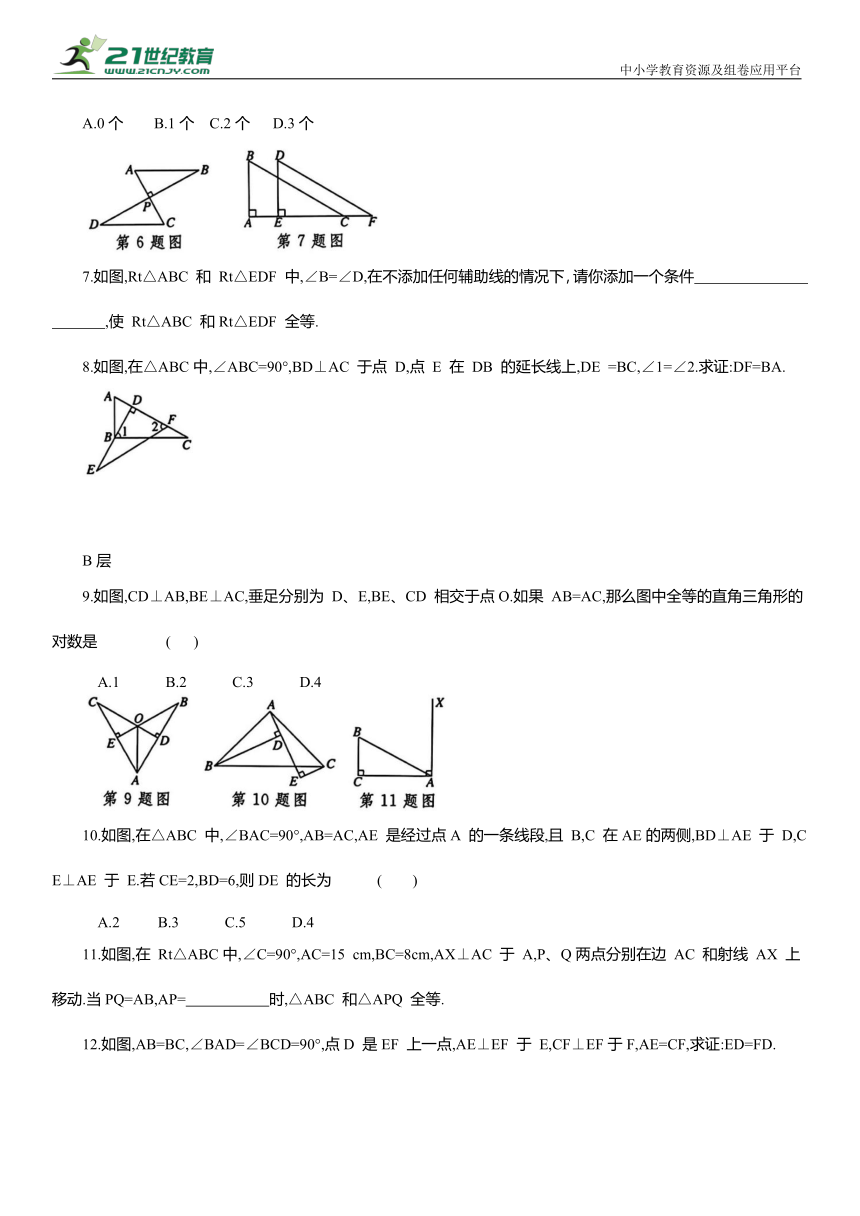
7.如图,Rt△ABC 和 Rt△EDF 中,∠B=∠D,在不添加任何辅助线的情况下,请你添加一个条件 ,使 Rt△ABC 和Rt△EDF 全等.
8.如图,在△ABC中,∠ABC=90°,BD⊥AC 于点 D,点 E 在 DB 的延长线上,DE =BC,∠1=∠2.求证:DF=BA.
B层
9.如图,CD⊥AB,BE⊥AC,垂足分别为 D、E,BE、CD 相交于点O.如果 AB=AC,那么图中全等的直角三角形的对数是 ( )
A.1 B.2 C.3 D.4
10.如图,在△ABC 中,∠BAC=90°,AB=AC,AE 是经过点A 的一条线段,且 B,C 在AE的两侧,BD⊥AE 于 D,CE⊥AE 于 E.若CE=2,BD=6,则DE 的长为 ( )
A.2 B.3 C.5 D.4
11.如图,在 Rt△ABC中,∠C=90°,AC=15 cm,BC=8cm,AX⊥AC 于 A,P、Q两点分别在边 AC 和射线 AX 上移动.当PQ=AB,AP= 时,△ABC 和△APQ 全等.
12.如图,AB=BC,∠BAD=∠BCD=90°,点D 是EF 上一点,AE⊥EF 于 E,CF⊥EF于F,AE=CF,求证:ED=FD.
13.如图,四边形 ABCD 中,AC 平分∠BAD,CB=CD,CF⊥AD交于 F.
(1)求证:∠ABC+∠ADC=180°;
(2)若AF=5,DF=2,求AB 的长.
C层
14.(1)如图①,在△ABC 中,∠ACB=90°.点 D在△ABC 外,连接 AD,作 DF⊥AB 交AB 于点 E,交 BC 于点 F,AD=AB,AE=AC,连接AF.求证:DF=BC+CF;
(2)如图②,AB=AD,AC=AE,∠ACB=∠AED=90°,延长 BC交 DE 于点 F,写出 DF、BC、CF 之间的数量关系,并证明你的结论.
第 4 课时 “斜边、直角边”
1. A 2. D 3.70°
4.证明:∵∠C = ∠D = 90°,∴△ACB 和△BDA 是直角 三角形.∴Rt△ACB≌Rt△BDA(HL).∴AD=BC.
5. B 6. D 7. AB=ED(答案不唯一)
8.证明:∵BD⊥AC 于 D,∴∠EDF =90°.∵∠1=∠2,∠1+∠C=90°,∠2+∠E=90°,∴∠E=∠C.在△DEF 和△BCA 中,
.∴ △DEF ≌ △BCA
(ASA).∴DF=BA.
9. C 10. D 11.8cm 或 15cm
12.证明:连接 BD.在 Rt△ABD 和 Rt△CBD中,(AB=CB,∴Rt△ABD ≌ Rt△CBD(HL).∴AD=CD.∵AE⊥EF 于 E,CF⊥EF 于 F,∴∠E=∠F=90°.在Rt△ADE 和Rt△CDF 中,JAD=CF,∴Rt△ADE≌Rt△CDF(HL).∴ED=FD.
13.(1)证明:如图,过点 C 作CE⊥AB,交AB 的延长线于E.∵CF⊥AD,∴∠CEA=∠CFA=90°.∵AC平分∠BAD,∴∠EAC=∠FAC. 在 △ACE 和 △ACF 中,BCERMW∠CPA,∴ △ACE ≌△AOF
(AAS). ∴ CE = CF.在 Rt△CBE 和Rt△CDF 中,FEE=CF,∴Rt△CBE≌Rt △CDF (HL). ∴ ∠ADC = ∠CBE.∵∠ABC+∠CBE = 180°, ∴∠ABC +∠ADC=180°.
(2)解:∵Rt△CBE≌Rt△CDF,∴DF=BE=2.∵△ACE≌△ACF,∴AE=AF=5.∴AB=AE-BE=3.
14.(1) 证 明: ∵ DE ⊥ AB,∠ACB = 90°,∴∠AED = ∠AEF = ∠ACB = 90°. 在Rt△ACF 与 Rt △AEF 中, ∴Rt△ACF≌Rt△AEF(HL).∴CF =EF. 在 Rt △ADE 与 Rt △ABC 中,ADE=AA,∴Rt△ADE≌ Rt △ABC(HL).∴DE = BC.∵DF = DE +EF,∴DF=BC+CF.
(2)解:BC=CF+DF,证明如下:如图②,连接 AF.在Rt△ABC与 Rt△ADE 中,AB=AD,∴ Rt△ABC≌Rt△ADE(HL).∴BC=DE.∵∠ACB= .在Rt△ACF与 Rt△AEF 中,AC=AE,∴R△ACF≌△AEF(HL).∴CF = EF.∵DE = EF +DF,∴BC=CF+DF.
第 4 课时 “斜边、直角边”
A层
知识点一 直角三角形全等的判定(“斜边、直角边”)
1.如图,已知 AC⊥BD,垂足为点 O,若 AO=CO,AB=CD,则 Rt△AOB≌Rt△COD,理由是 ( )
A. HL B. SAS C. ASA D. AAS
2.如图,BE=CF,AE⊥BC,DF⊥BC,垂足分别为点 E,F,要根据“HL”证明 Rt△ABE≌Rt△DCF,则还需要添加的一个条件是 ( )
A. AE=DF B.∠A=∠D
C.∠B=∠C D. AB=DC
3.如图,在四边形ABCD 中,CD=CB,∠B=∠D=90°,∠BAC=55°,则∠BCD 的度数为
4.如图,已知∠C=∠D=90°,BC 与AD 交于点E,AC=BD.求证:AD=BC.
知识点二 直角三角形全等的综合判定
5.下列条件中,不能判定两个直角三角形全等的是 ( )
A.斜边和一直角边对应相等
B.两个锐角对应相等
C.一锐角和斜边对应相等
D.两条直角边对应相等
6.如图,AC⊥BD 于 P,AP=CP,增加下列一个条件:①BP=DP;②AB=CD;③∠A=∠C.其中能判定△ABP≌△CDP 的条件有 ( )
A.0个 B.1个 C.2个 D.3个
7.如图,Rt△ABC 和 Rt△EDF 中,∠B=∠D,在不添加任何辅助线的情况下,请你添加一个条件 ,使 Rt△ABC 和Rt△EDF 全等.
8.如图,在△ABC中,∠ABC=90°,BD⊥AC 于点 D,点 E 在 DB 的延长线上,DE =BC,∠1=∠2.求证:DF=BA.
B层
9.如图,CD⊥AB,BE⊥AC,垂足分别为 D、E,BE、CD 相交于点O.如果 AB=AC,那么图中全等的直角三角形的对数是 ( )
A.1 B.2 C.3 D.4
10.如图,在△ABC 中,∠BAC=90°,AB=AC,AE 是经过点A 的一条线段,且 B,C 在AE的两侧,BD⊥AE 于 D,CE⊥AE 于 E.若CE=2,BD=6,则DE 的长为 ( )
A.2 B.3 C.5 D.4
11.如图,在 Rt△ABC中,∠C=90°,AC=15 cm,BC=8cm,AX⊥AC 于 A,P、Q两点分别在边 AC 和射线 AX 上移动.当PQ=AB,AP= 时,△ABC 和△APQ 全等.
12.如图,AB=BC,∠BAD=∠BCD=90°,点D 是EF 上一点,AE⊥EF 于 E,CF⊥EF于F,AE=CF,求证:ED=FD.
13.如图,四边形 ABCD 中,AC 平分∠BAD,CB=CD,CF⊥AD交于 F.
(1)求证:∠ABC+∠ADC=180°;
(2)若AF=5,DF=2,求AB 的长.
C层
14.(1)如图①,在△ABC 中,∠ACB=90°.点 D在△ABC 外,连接 AD,作 DF⊥AB 交AB 于点 E,交 BC 于点 F,AD=AB,AE=AC,连接AF.求证:DF=BC+CF;
(2)如图②,AB=AD,AC=AE,∠ACB=∠AED=90°,延长 BC交 DE 于点 F,写出 DF、BC、CF 之间的数量关系,并证明你的结论.
第 4 课时 “斜边、直角边”
1. A 2. D 3.70°
4.证明:∵∠C = ∠D = 90°,∴△ACB 和△BDA 是直角 三角形.∴Rt△ACB≌Rt△BDA(HL).∴AD=BC.
5. B 6. D 7. AB=ED(答案不唯一)
8.证明:∵BD⊥AC 于 D,∴∠EDF =90°.∵∠1=∠2,∠1+∠C=90°,∠2+∠E=90°,∴∠E=∠C.在△DEF 和△BCA 中,
.∴ △DEF ≌ △BCA
(ASA).∴DF=BA.
9. C 10. D 11.8cm 或 15cm
12.证明:连接 BD.在 Rt△ABD 和 Rt△CBD中,(AB=CB,∴Rt△ABD ≌ Rt△CBD(HL).∴AD=CD.∵AE⊥EF 于 E,CF⊥EF 于 F,∴∠E=∠F=90°.在Rt△ADE 和Rt△CDF 中,JAD=CF,∴Rt△ADE≌Rt△CDF(HL).∴ED=FD.
13.(1)证明:如图,过点 C 作CE⊥AB,交AB 的延长线于E.∵CF⊥AD,∴∠CEA=∠CFA=90°.∵AC平分∠BAD,∴∠EAC=∠FAC. 在 △ACE 和 △ACF 中,BCERMW∠CPA,∴ △ACE ≌△AOF
(AAS). ∴ CE = CF.在 Rt△CBE 和Rt△CDF 中,FEE=CF,∴Rt△CBE≌Rt △CDF (HL). ∴ ∠ADC = ∠CBE.∵∠ABC+∠CBE = 180°, ∴∠ABC +∠ADC=180°.
(2)解:∵Rt△CBE≌Rt△CDF,∴DF=BE=2.∵△ACE≌△ACF,∴AE=AF=5.∴AB=AE-BE=3.
14.(1) 证 明: ∵ DE ⊥ AB,∠ACB = 90°,∴∠AED = ∠AEF = ∠ACB = 90°. 在Rt△ACF 与 Rt △AEF 中, ∴Rt△ACF≌Rt△AEF(HL).∴CF =EF. 在 Rt △ADE 与 Rt △ABC 中,ADE=AA,∴Rt△ADE≌ Rt △ABC(HL).∴DE = BC.∵DF = DE +EF,∴DF=BC+CF.
(2)解:BC=CF+DF,证明如下:如图②,连接 AF.在Rt△ABC与 Rt△ADE 中,AB=AD,∴ Rt△ABC≌Rt△ADE(HL).∴BC=DE.∵∠ACB= .在Rt△ACF与 Rt△AEF 中,AC=AE,∴R△ACF≌△AEF(HL).∴CF = EF.∵DE = EF +DF,∴BC=CF+DF.
