12.2 三角形全等的判定第1课时 “边边边” 同步练习(含答案)2024—2025学年人教版数学八年级上册
文档属性
| 名称 | 12.2 三角形全等的判定第1课时 “边边边” 同步练习(含答案)2024—2025学年人教版数学八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 477.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-31 00:00:00 | ||
图片预览

文档简介
12.2 三角形全等的判定
第1课时 “边边边”
A层
知识点一 三角形全等的判定(“边边边”)
1.下列判断两个三角形全等的条件中,正确的是( )
A.一条边对应相等 B.两条边对应相等
C.三个角对应相等 D.三条边对应相等
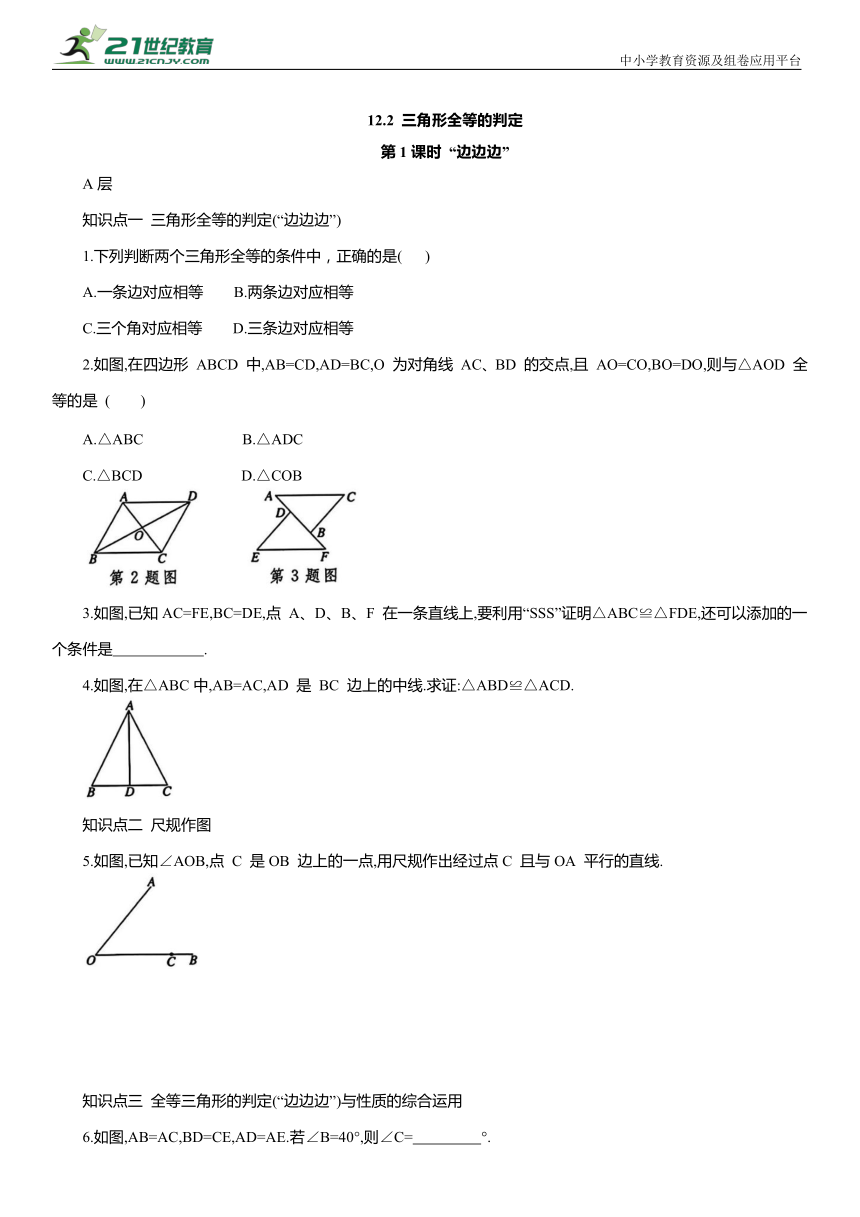
2.如图,在四边形 ABCD 中,AB=CD,AD=BC,O 为对角线 AC、BD 的交点,且 AO=CO,BO=DO,则与△AOD 全等的是 ( )
A.△ABC B.△ADC
C.△BCD D.△COB
3.如图,已知AC=FE,BC=DE,点 A、D、B、F 在一条直线上,要利用“SSS”证明△ABC≌△FDE,还可以添加的一个条件是 .
4.如图,在△ABC中,AB=AC,AD 是 BC 边上的中线.求证:△ABD≌△ACD.
知识点二 尺规作图
5.如图,已知∠AOB,点 C 是OB 边上的一点,用尺规作出经过点C 且与OA 平行的直线.
知识点三 全等三角形的判定(“边边边”)与性质的综合运用
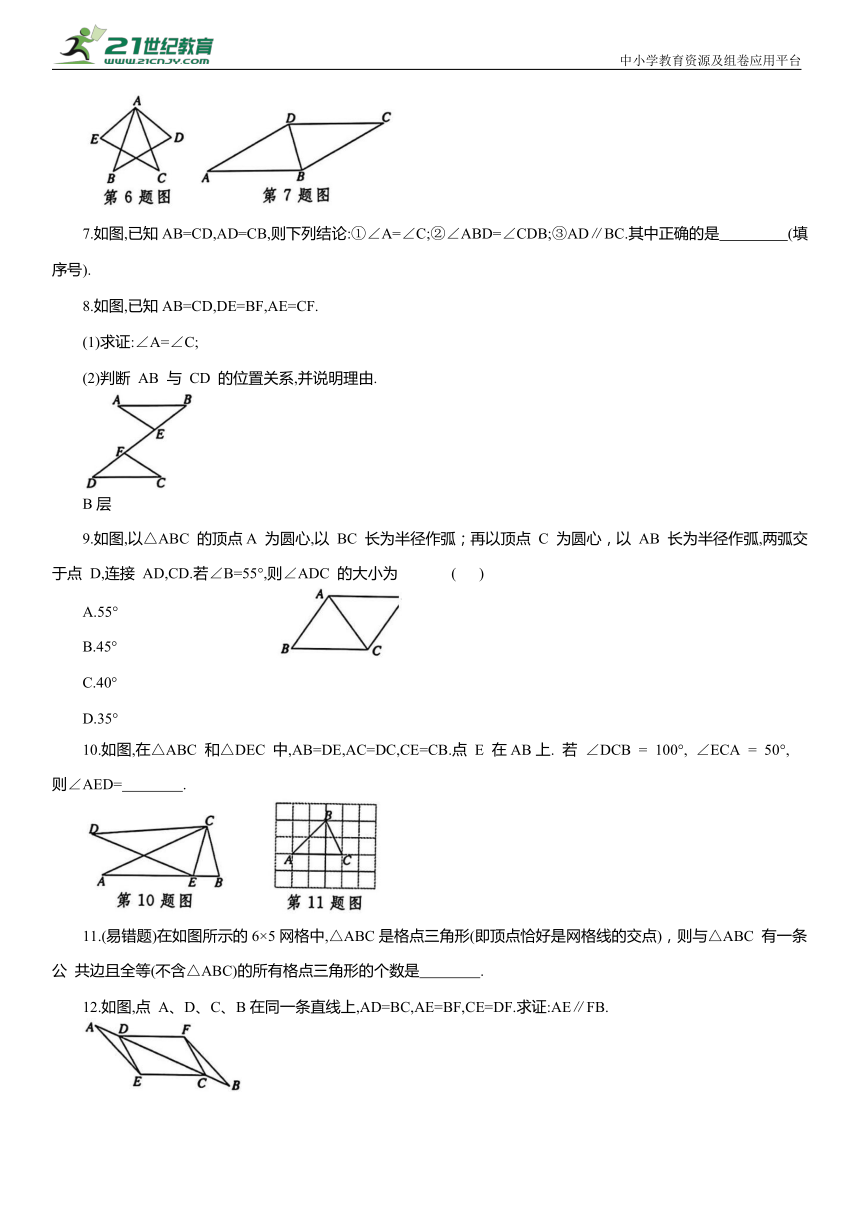
6.如图,AB=AC,BD=CE,AD=AE.若∠B=40°,则∠C= °.
7.如图,已知AB=CD,AD=CB,则下列结论:①∠A=∠C;②∠ABD=∠CDB;③AD∥BC.其中正确的是 (填序号).
8.如图,已知AB=CD,DE=BF,AE=CF.
(1)求证:∠A=∠C;
(2)判断 AB 与 CD 的位置关系,并说明理由.
B层
9.如图,以△ABC 的顶点A 为圆心,以 BC 长为半径作弧;再以顶点 C 为圆心,以 AB 长为半径作弧,两弧交于点 D,连接 AD,CD.若∠B=55°,则∠ADC 的大小为 ( )
A.55°
B.45°
C.40°
D.35°
10.如图,在△ABC 和△DEC 中,AB=DE,AC=DC,CE=CB.点 E 在AB上. 若 ∠DCB = 100°, ∠ECA = 50°, 则∠AED= .
11.(易错题)在如图所示的6×5网格中,△ABC是格点三角形(即顶点恰好是网格线的交点),则与△ABC 有一条公 共边且全等(不含△ABC)的所有格点三角形的个数是 .
12.如图,点 A、D、C、B在同一条直线上,AD=BC,AE=BF,CE=DF.求证:AE∥FB.
13.如图,AB=AC,BD=CD.
(1)求证:∠B=∠C;
(2)若∠A=2∠B,求证:∠BDC=4∠C.
C层
14.如图,在平面直角坐标系中,已知A(-1,3),B(-3,-2),C(3,-2),D(5,3),AB=CD,点 E,F 分别在AB,CD 上,试判断∠BEF和∠DFE 的大小关系,并说明理由.
中小学教育资源及组卷应用平台
第1课时 “边边边”
1. D 2. D 3. AB=DF(或AD=BF)
4.证明:∵AD 是BC 边上的中线,∴BD=CD.在 △ABD 和 △ACD 中, ∴△ABD≌△ACD(SSS).
5.解:如图,①以点 O 为圆心,任意长为半径画弧,交 OA 于点 E,交 OB 于点D;②以点 C 为圆心,OD 的长为半径画弧,交OB 于点G;③以点 G 为圆心,DE 的长为半径画弧,交前弧于点 H,作直线 CH,则CH∥OA.
6.40 7.①②③
8.(1)证明:∵DE=BF,∴DE--EF=BF-EF,即 DF =BE.在△ABE 和△CDF 中,
∴∠A=∠C.
(2)解:AB∥CD.理由如下:∵△ABE≌△CDF,∴∠B=∠D.∴AB∥CD.
9. A 10.25° 11.7
12.证明:∵AD=BC,∴AC=BD.在△ACE和 △BDF 中,△BDF(SSS).∴∠A=∠B.∴AE∥BF.
13.证明:(1)连接 AD 并延长至 E,如 图 所 示.在△ABD 和△ACD 中,
∴△ABD≌△ACD(SSS).∴∠B=∠C.
(2)∵∠BDE =∠BAD+∠B,∠CDE=∠CAD + ∠C, ∴∠BDC= ∠BDE +∠CDE=∠BAD+∠CAD+∠B+∠C,即∠BDC=∠BAC+∠B+∠C.∵∠BAC=2∠B,∠B=∠C,∴∠BDC=4∠C.
14.思路分析:
解:∠BEF=∠DFE.理由如下:如图,连接 BD.∵A(--1,3),D(5,3),∴AD=6.∵B(-3,-2),C(3,-2),∴BC=6.∴AD=BC.在△ABD 和△CDB 中,(SSS).∴∠ABD = ∠CDB.∴AB ∥CD.∴∠BEF=∠DFE.
第1课时 “边边边”
A层
知识点一 三角形全等的判定(“边边边”)
1.下列判断两个三角形全等的条件中,正确的是( )
A.一条边对应相等 B.两条边对应相等
C.三个角对应相等 D.三条边对应相等
2.如图,在四边形 ABCD 中,AB=CD,AD=BC,O 为对角线 AC、BD 的交点,且 AO=CO,BO=DO,则与△AOD 全等的是 ( )
A.△ABC B.△ADC
C.△BCD D.△COB
3.如图,已知AC=FE,BC=DE,点 A、D、B、F 在一条直线上,要利用“SSS”证明△ABC≌△FDE,还可以添加的一个条件是 .
4.如图,在△ABC中,AB=AC,AD 是 BC 边上的中线.求证:△ABD≌△ACD.
知识点二 尺规作图
5.如图,已知∠AOB,点 C 是OB 边上的一点,用尺规作出经过点C 且与OA 平行的直线.
知识点三 全等三角形的判定(“边边边”)与性质的综合运用
6.如图,AB=AC,BD=CE,AD=AE.若∠B=40°,则∠C= °.
7.如图,已知AB=CD,AD=CB,则下列结论:①∠A=∠C;②∠ABD=∠CDB;③AD∥BC.其中正确的是 (填序号).
8.如图,已知AB=CD,DE=BF,AE=CF.
(1)求证:∠A=∠C;
(2)判断 AB 与 CD 的位置关系,并说明理由.
B层
9.如图,以△ABC 的顶点A 为圆心,以 BC 长为半径作弧;再以顶点 C 为圆心,以 AB 长为半径作弧,两弧交于点 D,连接 AD,CD.若∠B=55°,则∠ADC 的大小为 ( )
A.55°
B.45°
C.40°
D.35°
10.如图,在△ABC 和△DEC 中,AB=DE,AC=DC,CE=CB.点 E 在AB上. 若 ∠DCB = 100°, ∠ECA = 50°, 则∠AED= .
11.(易错题)在如图所示的6×5网格中,△ABC是格点三角形(即顶点恰好是网格线的交点),则与△ABC 有一条公 共边且全等(不含△ABC)的所有格点三角形的个数是 .
12.如图,点 A、D、C、B在同一条直线上,AD=BC,AE=BF,CE=DF.求证:AE∥FB.
13.如图,AB=AC,BD=CD.
(1)求证:∠B=∠C;
(2)若∠A=2∠B,求证:∠BDC=4∠C.
C层
14.如图,在平面直角坐标系中,已知A(-1,3),B(-3,-2),C(3,-2),D(5,3),AB=CD,点 E,F 分别在AB,CD 上,试判断∠BEF和∠DFE 的大小关系,并说明理由.
中小学教育资源及组卷应用平台
第1课时 “边边边”
1. D 2. D 3. AB=DF(或AD=BF)
4.证明:∵AD 是BC 边上的中线,∴BD=CD.在 △ABD 和 △ACD 中, ∴△ABD≌△ACD(SSS).
5.解:如图,①以点 O 为圆心,任意长为半径画弧,交 OA 于点 E,交 OB 于点D;②以点 C 为圆心,OD 的长为半径画弧,交OB 于点G;③以点 G 为圆心,DE 的长为半径画弧,交前弧于点 H,作直线 CH,则CH∥OA.
6.40 7.①②③
8.(1)证明:∵DE=BF,∴DE--EF=BF-EF,即 DF =BE.在△ABE 和△CDF 中,
∴∠A=∠C.
(2)解:AB∥CD.理由如下:∵△ABE≌△CDF,∴∠B=∠D.∴AB∥CD.
9. A 10.25° 11.7
12.证明:∵AD=BC,∴AC=BD.在△ACE和 △BDF 中,△BDF(SSS).∴∠A=∠B.∴AE∥BF.
13.证明:(1)连接 AD 并延长至 E,如 图 所 示.在△ABD 和△ACD 中,
∴△ABD≌△ACD(SSS).∴∠B=∠C.
(2)∵∠BDE =∠BAD+∠B,∠CDE=∠CAD + ∠C, ∴∠BDC= ∠BDE +∠CDE=∠BAD+∠CAD+∠B+∠C,即∠BDC=∠BAC+∠B+∠C.∵∠BAC=2∠B,∠B=∠C,∴∠BDC=4∠C.
14.思路分析:
解:∠BEF=∠DFE.理由如下:如图,连接 BD.∵A(--1,3),D(5,3),∴AD=6.∵B(-3,-2),C(3,-2),∴BC=6.∴AD=BC.在△ABD 和△CDB 中,(SSS).∴∠ABD = ∠CDB.∴AB ∥CD.∴∠BEF=∠DFE.
