第十二章全等三角形考点整合训练 (含答案) 2024—2025学年人教版数学八年级上册
文档属性
| 名称 | 第十二章全等三角形考点整合训练 (含答案) 2024—2025学年人教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 465.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-31 06:18:29 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第十二章全等三角形考点整合训练
考点一 全等三角形的性质与判定
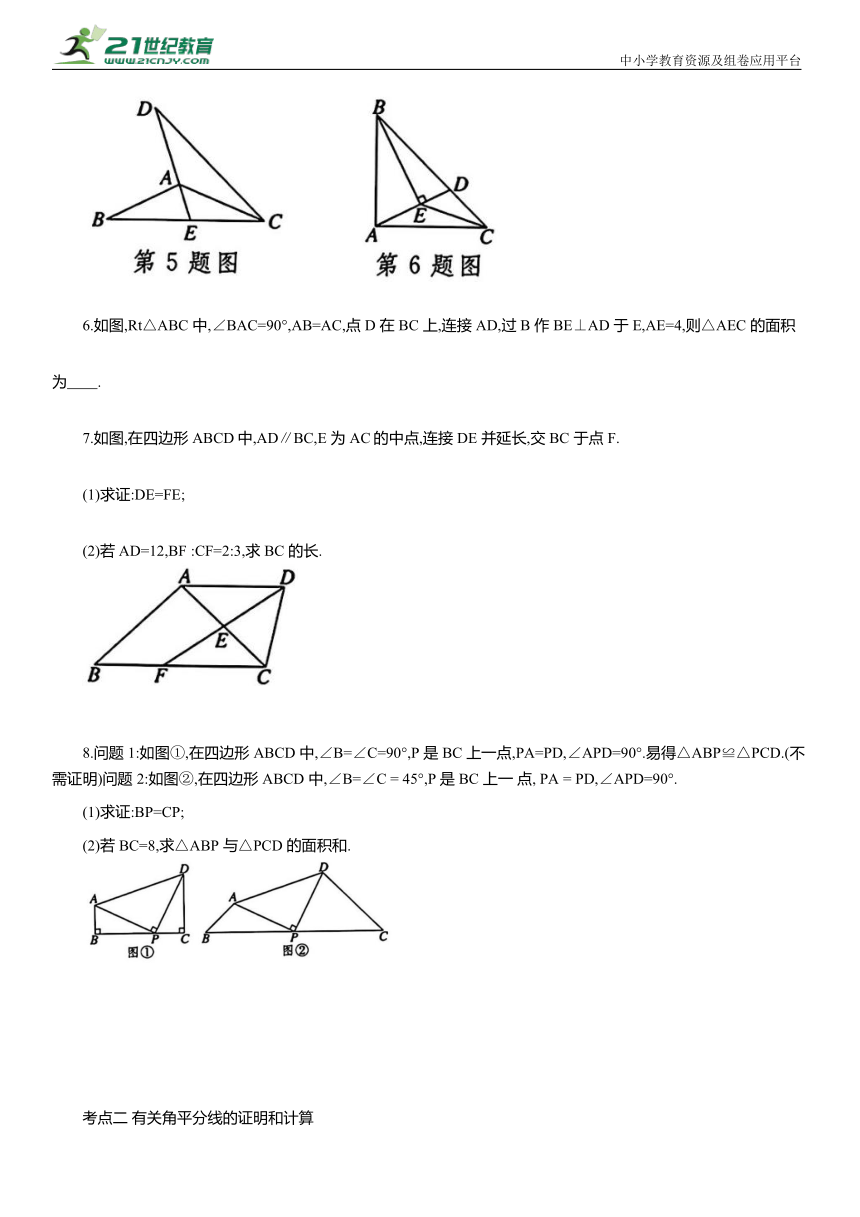
1.已知图中两个三角形全等,则∠1 等于 ( )
A.40° B.50° C.60° D.80°
2.如图,AB =EF,AC= ED,∠A =∠E.若BF=10,CF=2,则CD的长为 ( )
A.8 B.7 C.6 D.5
3.如图,一名工作人员不慎将一块三角形模具打碎成三块,他要带其中一块或两块碎片到商店去配一块与原来一样的三角形模具,他带哪块去最省事 ( )
A.① B.② C.③ D.①③
4.如图,四边形 ABCD 中,∠BAC=∠DAC,请补充一个条件 ,使△ABC≌△ADC.
5.如图,CA 平分∠DCB,CB=CD,DA 的延长线交 BC于点 E.若∠EAC=49°,则∠BAE 的度数为 .
6.如图,Rt△ABC 中,∠BAC=90°,AB=AC,点 D 在 BC 上,连接 AD,过 B 作 BE⊥AD 于E,AE=4,则△AEC 的面积为 .
7.如图,在四边形ABCD中,AD∥BC,E 为AC的中点,连接 DE 并延长,交 BC 于点 F.
(1)求证:DE=FE;
(2)若AD=12,BF :CF=2:3,求 BC 的长.
8.问题1:如图①,在四边形 ABCD 中,∠B=∠C=90°,P 是 BC 上一点,PA=PD,∠APD=90°.易得△ABP≌△PCD.(不需证明)问题 2:如图②,在四边形 ABCD 中,∠B=∠C = 45°,P 是 BC 上一 点, PA = PD,∠APD=90°.
(1)求证:BP=CP;
(2)若 BC=8,求△ABP 与△PCD 的面积和.
考点二 有关角平分线的证明和计算
9.如图,在 Rt△ABC中,∠B=90°,作图痕迹如图所示.若 BG=1,AC=4,则△ACG 的面积是 ( )
A.1 B. C.2 D.
10.如图,Rt△ABC 中,∠ABC=90°,AB=6,BC=8,BD 为△ABC 的角平分线,则点 D到边AB 的距离为 .
11.如图,OB 平分∠MON,A为 OB 的中点,AE⊥ON 于点 E,AE=4,D 为 OM 上一点,BC∥OM 交 DA 的延长线于点 C,则 CD 的最小值为 .
12.如图,在△ABC中,AK,BK,CK 分别平分∠BAC,∠ABC,∠ACB,KD⊥BC于点D,求证:AB-AC=BD-CD.
考点三 全等三角形的实际应用
13.如图,有两个长度相等的滑梯 BC 与 EF,滑梯 BC 的高AC 与滑梯EF 的水平距离 DF的长度相等,问两个滑梯的倾斜角∠B 与∠F 的大小有什么关系 请说明理由.
考点整合训练
1. A 2. C 3. C 4. AB=AD(答案不唯一)5.82° 6.8
7.(1)证明:∵E 为AC 的中点,∴AE=CE.∵AD∥BC,∴∠EAD=∠ECF,∠EDA=∠EFC. 在 △EAD 和 △ECF 中,
(AAS).∴DE=FE.
(2)解:由(1)得△EAD≌△ECF,∴CF=AD=12.∵BF : CF=2 : 3,∴BF =8.∴BC=BF+CF=8+12=20.
8.(1)证明:如图②,过点 A 作AE⊥BC 于 E,过点 D 作DF⊥BC 于 F.由题易得△AEP≌△PFD,∴AE=PF,EP=DF.∵∠B =∠C=45°,AE⊥BC,DF⊥BC,∴∠B =∠BAE=45°,∠C=∠CDF=45°,即△AEB和△CDF 均为等腰直角三角形.∴BE =AE=PF,CF=DF=EP.∴BE+EP =PF+CF.∴BP=CP.
(2)解:由(1)得
9. C 10.
11.8 解析:∵BC∥OM,∴∠B=∠DOA.∵ A 为 OB 的 中 点, ∴ AB = AO.∵∠BAC=∠DAO,∴△ABC≌△AOD(ASA).∴AC=AD.∴CD=2AD.∴当AD有最小值时,CD 有最小值.∴当AD⊥OM时,AD 有 最小值.∵OB 平 分 ∠MON,AE⊥ON,AD⊥OM,∴AD =AE =4.∴CD的最小值为8.
12.证明:如图,作 KE⊥AB 于E,KF⊥AC 于点 F.∵AK平 分 ∠BAC, KE ⊥ AB,KF⊥AC,∴KE= KF.在 Rt△AKE 和Rt△AKF 中,AK=AK,∴Rt△AKE≌Rt△AKF(HL).∴AE= AF.同理可得BE=BD,CD=CF.∴AB-AC=AE+BE-AF-CF=BE-CF=BD-CD.
13.解:∠B 与∠F 互余.理由如下:在 Rt△ABC和 Rt△DEF 中, ∴Rt△ABC≌Rt △DEF ( HL ). ∴ ∠B = ∠DEF.又∵∠DEF+∠F=90°,∴∠B+∠F=90°,即两滑梯的倾斜角∠B 与∠F 互余.
第十二章全等三角形考点整合训练
考点一 全等三角形的性质与判定
1.已知图中两个三角形全等,则∠1 等于 ( )
A.40° B.50° C.60° D.80°
2.如图,AB =EF,AC= ED,∠A =∠E.若BF=10,CF=2,则CD的长为 ( )
A.8 B.7 C.6 D.5
3.如图,一名工作人员不慎将一块三角形模具打碎成三块,他要带其中一块或两块碎片到商店去配一块与原来一样的三角形模具,他带哪块去最省事 ( )
A.① B.② C.③ D.①③
4.如图,四边形 ABCD 中,∠BAC=∠DAC,请补充一个条件 ,使△ABC≌△ADC.
5.如图,CA 平分∠DCB,CB=CD,DA 的延长线交 BC于点 E.若∠EAC=49°,则∠BAE 的度数为 .
6.如图,Rt△ABC 中,∠BAC=90°,AB=AC,点 D 在 BC 上,连接 AD,过 B 作 BE⊥AD 于E,AE=4,则△AEC 的面积为 .
7.如图,在四边形ABCD中,AD∥BC,E 为AC的中点,连接 DE 并延长,交 BC 于点 F.
(1)求证:DE=FE;
(2)若AD=12,BF :CF=2:3,求 BC 的长.
8.问题1:如图①,在四边形 ABCD 中,∠B=∠C=90°,P 是 BC 上一点,PA=PD,∠APD=90°.易得△ABP≌△PCD.(不需证明)问题 2:如图②,在四边形 ABCD 中,∠B=∠C = 45°,P 是 BC 上一 点, PA = PD,∠APD=90°.
(1)求证:BP=CP;
(2)若 BC=8,求△ABP 与△PCD 的面积和.
考点二 有关角平分线的证明和计算
9.如图,在 Rt△ABC中,∠B=90°,作图痕迹如图所示.若 BG=1,AC=4,则△ACG 的面积是 ( )
A.1 B. C.2 D.
10.如图,Rt△ABC 中,∠ABC=90°,AB=6,BC=8,BD 为△ABC 的角平分线,则点 D到边AB 的距离为 .
11.如图,OB 平分∠MON,A为 OB 的中点,AE⊥ON 于点 E,AE=4,D 为 OM 上一点,BC∥OM 交 DA 的延长线于点 C,则 CD 的最小值为 .
12.如图,在△ABC中,AK,BK,CK 分别平分∠BAC,∠ABC,∠ACB,KD⊥BC于点D,求证:AB-AC=BD-CD.
考点三 全等三角形的实际应用
13.如图,有两个长度相等的滑梯 BC 与 EF,滑梯 BC 的高AC 与滑梯EF 的水平距离 DF的长度相等,问两个滑梯的倾斜角∠B 与∠F 的大小有什么关系 请说明理由.
考点整合训练
1. A 2. C 3. C 4. AB=AD(答案不唯一)5.82° 6.8
7.(1)证明:∵E 为AC 的中点,∴AE=CE.∵AD∥BC,∴∠EAD=∠ECF,∠EDA=∠EFC. 在 △EAD 和 △ECF 中,
(AAS).∴DE=FE.
(2)解:由(1)得△EAD≌△ECF,∴CF=AD=12.∵BF : CF=2 : 3,∴BF =8.∴BC=BF+CF=8+12=20.
8.(1)证明:如图②,过点 A 作AE⊥BC 于 E,过点 D 作DF⊥BC 于 F.由题易得△AEP≌△PFD,∴AE=PF,EP=DF.∵∠B =∠C=45°,AE⊥BC,DF⊥BC,∴∠B =∠BAE=45°,∠C=∠CDF=45°,即△AEB和△CDF 均为等腰直角三角形.∴BE =AE=PF,CF=DF=EP.∴BE+EP =PF+CF.∴BP=CP.
(2)解:由(1)得
9. C 10.
11.8 解析:∵BC∥OM,∴∠B=∠DOA.∵ A 为 OB 的 中 点, ∴ AB = AO.∵∠BAC=∠DAO,∴△ABC≌△AOD(ASA).∴AC=AD.∴CD=2AD.∴当AD有最小值时,CD 有最小值.∴当AD⊥OM时,AD 有 最小值.∵OB 平 分 ∠MON,AE⊥ON,AD⊥OM,∴AD =AE =4.∴CD的最小值为8.
12.证明:如图,作 KE⊥AB 于E,KF⊥AC 于点 F.∵AK平 分 ∠BAC, KE ⊥ AB,KF⊥AC,∴KE= KF.在 Rt△AKE 和Rt△AKF 中,AK=AK,∴Rt△AKE≌Rt△AKF(HL).∴AE= AF.同理可得BE=BD,CD=CF.∴AB-AC=AE+BE-AF-CF=BE-CF=BD-CD.
13.解:∠B 与∠F 互余.理由如下:在 Rt△ABC和 Rt△DEF 中, ∴Rt△ABC≌Rt △DEF ( HL ). ∴ ∠B = ∠DEF.又∵∠DEF+∠F=90°,∴∠B+∠F=90°,即两滑梯的倾斜角∠B 与∠F 互余.
