模型构建专题:全等三角形中常见的解题模型 同步练习 (含答案)2024—2025学年人教版数学八年级上册
文档属性
| 名称 | 模型构建专题:全等三角形中常见的解题模型 同步练习 (含答案)2024—2025学年人教版数学八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 293.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-31 06:18:14 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
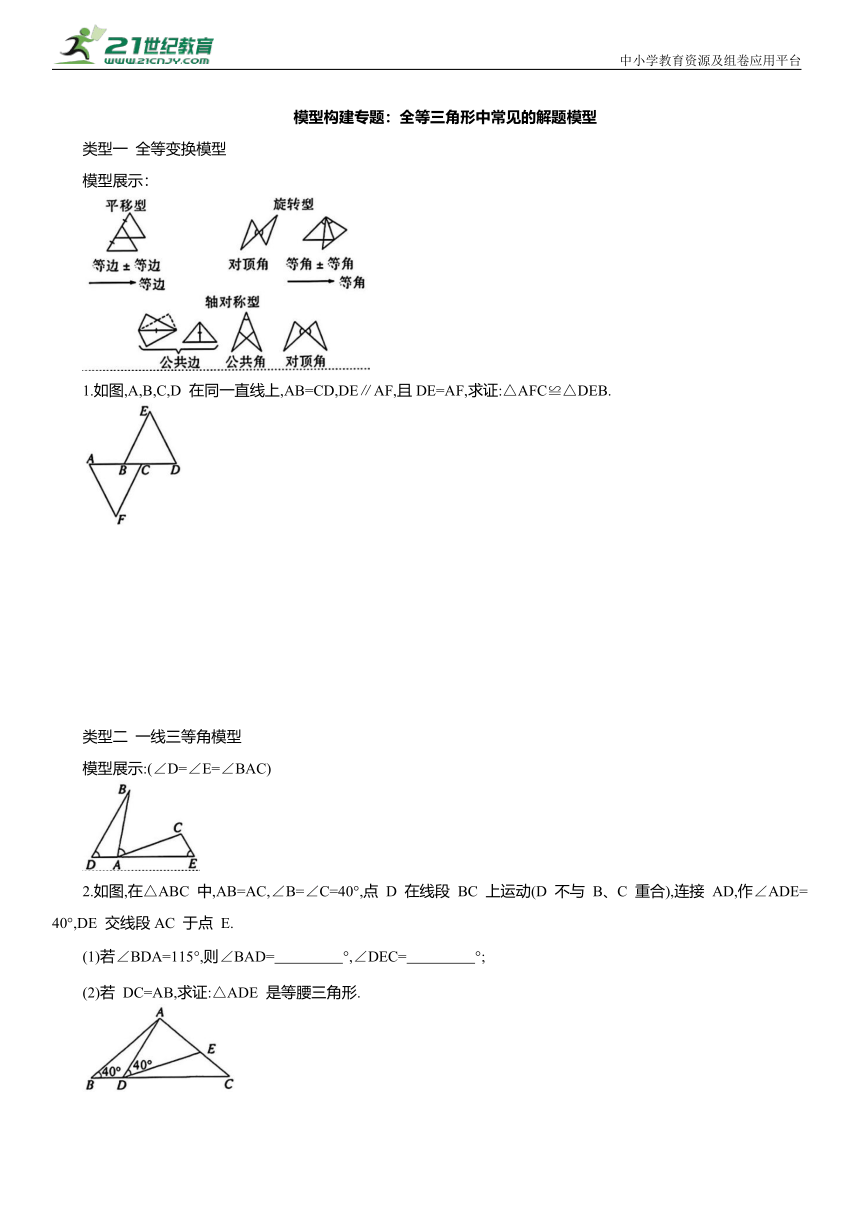
模型构建专题:全等三角形中常见的解题模型
类型一 全等变换模型
模型展示:
1.如图,A,B,C,D 在同一直线上,AB=CD,DE∥AF,且DE=AF,求证:△AFC≌△DEB.
类型二 一线三等角模型
模型展示:(∠D=∠E=∠BAC)
2.如图,在△ABC 中,AB=AC,∠B=∠C=40°,点 D 在线段 BC 上运动(D 不与 B、C 重合),连接 AD,作∠ADE=40°,DE 交线段AC 于点 E.
(1)若∠BDA=115°,则∠BAD= °,∠DEC= °;
(2)若 DC=AB,求证:△ADE 是等腰三角形.
类型三 垂直模型
模型展示:
3.如图,直线 MN 一侧有一个等腰 Rt△ABC,其中∠ACB=90°,CA=CB.直线 MN 过顶点C,分别过点 A,B 作AE⊥MN,BF⊥MN,垂足分别为点 E,F,∠CAB 的平分线AG 交BC于点 O,交 MN 于点G,连接 BG,恰好满足AG⊥BG.延长 AC,BG 交于点 D.求证:
(1)CE=BF;
(2)AC+CO=AB.
模型构建专题:全等三角形中常见的解题模型
1.证明:∵AB=CD,∴AB+BC=CD+BC,即AC=BD.∵DE∥AF,∴∠A=∠D.在△AFC 和 △DEB 中, ∴△AFC≌△DEB(SAS).
2.(1)25 115
(2)证明:∵∠ADC=∠EDC+∠EDA=∠DAB + ∠B, ∠B = ∠EDA = 40°,
∴∠EDC=∠DAB.∴△ABD ≌△DCE
(ASA).∴AD=DE,即△ADE 是等腰三角形.
3.证明:(1)∵AE⊥MN,BF⊥MN,∠ACB=
90°, ∴ ∠EAC + ∠ECA = ∠FCB +
∠ECA=90°.∴∠EAC=∠FCB.在△AEC
和 △CFB 中,
∴△AEC≌△CFB(AAS).∴CE=BF.
(2)∵∠ACB=90°,AG⊥BG,∴∠CAO+
∠D = ∠CBD + ∠D = 90°.∴∠CAO =
∠CBD. ∴△ACO≌△BCD(ASA).∴CO=CD.∴AC +CO=AC+CD=AD.∵AG 平分∠CAB,AG⊥BG,
∴∠DAG=∠BAG,∠AGB=∠AGD=90°.
在△AGD 和△AGB 中
∴△AGD ≌△AGB(ASA).∴AD= AB.
∴AC+CO=AB.
模型构建专题:全等三角形中常见的解题模型
类型一 全等变换模型
模型展示:
1.如图,A,B,C,D 在同一直线上,AB=CD,DE∥AF,且DE=AF,求证:△AFC≌△DEB.
类型二 一线三等角模型
模型展示:(∠D=∠E=∠BAC)
2.如图,在△ABC 中,AB=AC,∠B=∠C=40°,点 D 在线段 BC 上运动(D 不与 B、C 重合),连接 AD,作∠ADE=40°,DE 交线段AC 于点 E.
(1)若∠BDA=115°,则∠BAD= °,∠DEC= °;
(2)若 DC=AB,求证:△ADE 是等腰三角形.
类型三 垂直模型
模型展示:
3.如图,直线 MN 一侧有一个等腰 Rt△ABC,其中∠ACB=90°,CA=CB.直线 MN 过顶点C,分别过点 A,B 作AE⊥MN,BF⊥MN,垂足分别为点 E,F,∠CAB 的平分线AG 交BC于点 O,交 MN 于点G,连接 BG,恰好满足AG⊥BG.延长 AC,BG 交于点 D.求证:
(1)CE=BF;
(2)AC+CO=AB.
模型构建专题:全等三角形中常见的解题模型
1.证明:∵AB=CD,∴AB+BC=CD+BC,即AC=BD.∵DE∥AF,∴∠A=∠D.在△AFC 和 △DEB 中, ∴△AFC≌△DEB(SAS).
2.(1)25 115
(2)证明:∵∠ADC=∠EDC+∠EDA=∠DAB + ∠B, ∠B = ∠EDA = 40°,
∴∠EDC=∠DAB.∴△ABD ≌△DCE
(ASA).∴AD=DE,即△ADE 是等腰三角形.
3.证明:(1)∵AE⊥MN,BF⊥MN,∠ACB=
90°, ∴ ∠EAC + ∠ECA = ∠FCB +
∠ECA=90°.∴∠EAC=∠FCB.在△AEC
和 △CFB 中,
∴△AEC≌△CFB(AAS).∴CE=BF.
(2)∵∠ACB=90°,AG⊥BG,∴∠CAO+
∠D = ∠CBD + ∠D = 90°.∴∠CAO =
∠CBD. ∴△ACO≌△BCD(ASA).∴CO=CD.∴AC +CO=AC+CD=AD.∵AG 平分∠CAB,AG⊥BG,
∴∠DAG=∠BAG,∠AGB=∠AGD=90°.
在△AGD 和△AGB 中
∴△AGD ≌△AGB(ASA).∴AD= AB.
∴AC+CO=AB.
